مشكلة القندس المشغول، وهي مشكلة في علوم الكمبيوتر استمرت لمدة أربعين عامًا، تم حلها أخيرًا على يد مجموعة من الهواة! لم يصدم هذا التطور الخارق المجتمع الأكاديمي فحسب، بل تم الاعتراف به أيضًا من قبل عالم الرياضيات الشهير تيرينس تاو، وتم الترحيب به باعتباره أهم تطور في هذا المجال منذ عام 1983. باستخدام مساعد إثبات Coq، نجحوا في التحقق من أن قيمة رقم القندس الخامس المشغول BB(5) هي 47,176,870، مما يدل على الإمكانات الكبيرة للإثبات بمساعدة البرامج في حل المشكلات الرياضية المعقدة، كما يزودنا برؤى حول سلوك آلة تورينج. ووقف المشاكل منظور جديد.
في مجال غامض من علوم الكمبيوتر، تم مؤخرًا حل مشكلة عمرها أربعون عامًا تسمى مشكلة القندس المشغول بنجاح من قبل مجموعة من الهواة. لم يُحدث هذا الإنجاز ضجة كبيرة في العالم الأكاديمي فحسب، بل تم الاعتراف به أيضًا من قبل عالم الرياضيات الشهير تيرينس تاو، الذي نشر الخبر على وسائل التواصل الاجتماعي وشدد على أهمية مساعدي الإثبات في البحث الرياضي.
كما أشاد عالم الكمبيوتر سكوت آرونسون بهذا الاكتشاف، معتقدًا أنه أهم تطور في أبحاث وظائف القندس المزدحمة منذ عام 1983. يمثل هذا الإنجاز فهمًا عميقًا لحدود النظرية الحسابية ويوضح إمكانات البراهين المدعومة بالبرمجيات في حل المشكلات الرياضية المعقدة.
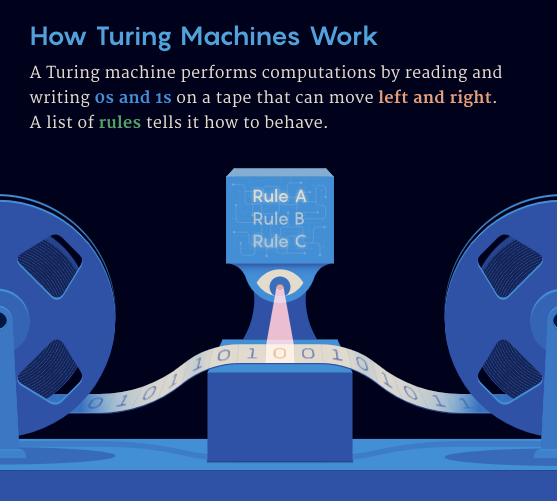
نشأت مشكلة القندس المزدحم منذ أكثر من 40 عامًا في دورتموند بألمانيا، عندما حاول علماء الكمبيوتر العثور على آلة تورينج محددة يمكنها كتابة أكبر عدد من الأرقام قبل التوقف. آلة تورينج هي نموذج حاسوبي تجريدي اقترحه آلان تورينج في عام 1936، ويقوم بإجراء العمليات الحسابية على شريط مغناطيسي طويل بلا حدود من خلال قراءة وكتابة الصفر والواحد.

بعد تحديد رقم القندس الرابع المزدحم في عام 1974، أصبح العثور على القندس الخامس سؤالًا مفتوحًا. الآن، نجح مجتمع عبر الإنترنت يضم أكثر من 20 مساهمًا من جميع أنحاء العالم، باستخدام برنامج مساعد الإثبات يسمى Coq، في التحقق من أن رقم Busy Beaver الخامس BB(5) له قيمة 47,176,870.
ولم يثير هذا الإنجاز حماس المجتمع فحسب، بل أثار دهشة عالم الكمبيوتر داميان وودز، الذي شبه التقدم بسرعة يوسين بولت. على الرغم من أن حل هذه المشكلة قد لا يكون قابلاً للتطبيق بشكل مباشر في مجالات أخرى من علوم الكمبيوتر، إلا أنه بالنسبة للمشاركين، فإن هذا الصراع ضد الاستحالة الرياضية هو أعظم مكافأة في حد ذاته.
يكمن جوهر مشكلة القندس المشغول في فهم سلوك آلات تورينج، وتحديدًا أدائها في حل المشكلات. يتم تحديد سلوك آلة تورينج من خلال مجموعة من القواعد، والتي يمكن تصورها كجدول. تحدد كل قاعدة الإجراء الذي يجب تنفيذه عندما يواجه رأس القراءة/الكتابة 0 أو 1 في حالة معينة.
على الرغم من أن آلات تورينج يمكن أن تتعطل في حلقات لا نهائية، فإن تحديد ما إذا كانت ستتوقف عن العمل أم لا هي مشكلة مشهورة لم يتم حلها. لم يكن عالم الرياضيات تيبور رادو راضيًا عن هذا الاستنتاج، وبالتالي اخترع "لعبة القندس المشغولة" لاستكشاف طبيعة مشكلة التوقف من خلال تجميع آلات تورينج وفقًا لعدد القواعد التي كانت لديها.
اكتشف الباحثون الأوائل، مثل ألين برادي، هذه المشكلة عن طريق كتابة برامج لمحاكاة سلوك آلات تورينج. وقد وضعت أعماله واكتشافات الباحثين الآخرين الأساس للمستكشفين اللاحقين.
حتى عام 2022، أطلقت طالبة الدراسات العليا تريستان ستيرين تحدي Busy Beaver، وهو مشروع تعاوني عبر الإنترنت يهدف إلى إنهاء BB(5). من خلال الأساليب المبتكرة ومساعدة مساعد Coq، نجح الفريق أخيرًا في العثور على القندس الخامس المزدحم.
ولا يمثل هذا الإنجاز تحديًا لاستحالة الرياضيات فحسب، بل يمثل أيضًا استكشافًا لحدود علوم الكمبيوتر. مع تأكيد BB(5)، يقوم الباحثون بصياغة ورقة أكاديمية ستكون نسخة يمكن قراءتها بواسطة الإنسان وتكمل إثبات Coq. وفي الوقت نفسه، يفكرون أيضًا فيما إذا كان استكشاف BB(6) سيصبح الهدف التالي.
المرجع: https://www.quantamagazine.org/amateur-mathematicians-find-fifth-busy-beaver-turing-machine-20240702/
إن حل مشكلة القندس المزدحم لا يعد إنجازًا كبيرًا في مجال الرياضيات فحسب، بل يوفر أيضًا اتجاهات وأفكارًا جديدة لأبحاث نظرية الحوسبة المستقبلية. يشجع هذا الإنجاز المزيد من الأشخاص على المشاركة في أبحاث الرياضيات وعلوم الكمبيوتر واستكشاف المجالات غير المعروفة معًا.