افتتح فريق مختبر شنغهاي AI مصدر إصدار Llama من مشروع O1 ، وهو مشروع متماثل مفتوح المصدر لأداة حل المشكلات Openai Olympiad O1. يستخدم المشروع تقنيات متقدمة مثل Monte Carlo Tree Search وتعلم التعزيز لتحقيق نتائج ملحوظة في الإجابة على أسئلة أولمبياد الرياضية ، وحتى أدائها يتجاوز بعض الحلول التجارية المغلقة. يوفر المصدر المفتوح للمشروع للمطورين مؤسسة تعليمية وبحوث قيمة ، كما يعزز تطوير مزيد من التطوير لتطبيق الذكاء الاصطناعي في مجال الرياضيات. يشتمل هذا المشروع على مجموعات بيانات مدربة مسبقًا ، ونماذج تدريبية مسبقة ، ورموز التدريب على التعلم التعزيز ، وما إلى ذلك ، ويستخدم مجموعة متنوعة من تقنيات التحسين بما في ذلك Lora و PPO ، بهدف تحسين قدرة النموذج في التفكير الرياضي.
في الآونة الأخيرة ، أصدر فريق مختبر شنغهاي AI إصدار Llama من مشروع O1 ، بهدف تكرار أداة حل المشكلات Openai Openai O1. يتبنى المشروع مجموعة متنوعة من التقنيات المتقدمة ، بما في ذلك Monte Carlo Tree Search ، وتعلم تعزيز اللعب الذاتي ، ونموذج الإستراتيجية المزدوجة لـ PPO و Alphago Zero ، والذي اجتذب اهتمامًا واسعًا من مجتمع المطورين.

قبل وقت طويل من إصدار سلسلة Openai's O1 ، بدأ فريق مختبر Shanghai AI في استكشاف استخدام Monte Carlo Tree Search لتحسين القدرة الرياضية للنماذج الكبيرة. بعد إصدار O1 ، قام الفريق بترقية الخوارزمية ، وركز على مشكلة Math Olympiad ، وقام بتطويرها كنسخة مفتوحة المصدر من مشروع Openai Strawberry.
من أجل تحسين أداء نموذج LLAMA في مشاكل الأوليمبياد الرياضية ، اعتمد الفريق استراتيجية التحسين المقترنة ، أي ، لا تعطي مباشرة النتيجة المطلقة للإجابة ، بل تقارن المزايا النسبية وعيوب الإجابات. مع هذا النهج ، حققوا تقدمًا كبيرًا في معايير Aime2024 الأكثر صعوبة. من بين 3 أسئلة الاختبار ، تم إجراء النموذج المحسن بشكل صحيح 8 ، في حين تم إجراء نموذج LLAMA-3.1-8B-8B الأصلي بشكل صحيح 2. يتفوق هذا الإنجاز على حلول أخرى مغلقة بالمصدر إلى جانب O1-Preview و O1-Mini.
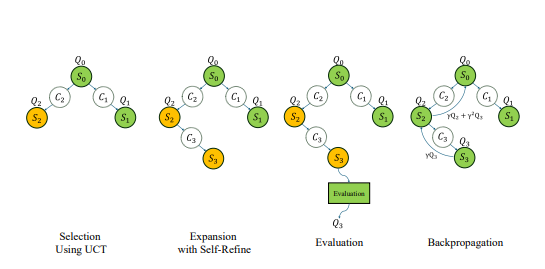
في نهاية شهر أكتوبر ، أعلن الفريق تقدمًا كبيرًا في تكرار Openai O1 استنادًا إلى بنية Alphago Zero ، مما سمح للنموذج بنجاح بكسب قدرة التفكير المتقدم من خلال التفاعل مع شجرة البحث أثناء عملية التعلم دون التعليق التوضيحي اليدوي. في أقل من أسبوع ، تم فتح المشروع.
في الوقت الحاضر ، يتضمن المحتوى المفتوح المصدر لإصدار Llama O1: مجموعات البيانات المدربة مسبقًا ، والنماذج التي تم تدريبها مسبقًا ، ورمز التدريب على التعلم التعزيز. من بينها ، تحتوي مجموعة بيانات "OpenLongCot-pretrain" على أكثر من 100000 من بيانات سلسلة التفكير الطويلة ، كل بيانات تحتوي على عملية التفكير في مشكلة رياضية كاملة ، بما في ذلك محتوى التفكير ، ونتائج التسجيل ، ووصف المشكلة ، وإحداثيات الرسم البياني ، وعملية الحساب ، وخصم الخلاصة وغيرها روابط الاستدلال الكاملة ، وكذلك النقد والتحقق من كل خطوة استنتاج ، توفر التقييم والتوجيه لعملية الاستدلال. بعد الاستمرار في التدريب المسبق على مجموعة البيانات هذه ، يمكن للنموذج قراءة وإخراج عمليات سلسلة التفكير الطويلة مثل O1.
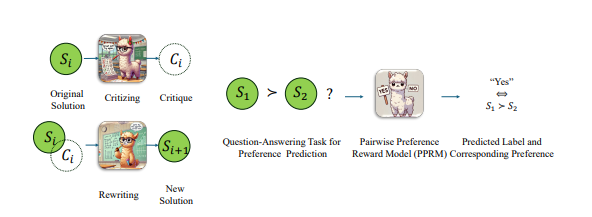
على الرغم من أن المشروع يسمى LLAMA-O1 ، فإن النموذج الذي تم تدريبه مسبقًا يقدمه المسؤول حاليًا يعتمد على GEMMA2 من Google. بناءً على النموذج الذي تم تدريبه مسبقًا ، يمكن للمطورين مواصلة تنفيذ التدريب على التعلم التعزيز. تتضمن عملية التدريب: استخدام Monte Carlo Tree لتوليد خبرة في التخزين في تجربة عازلة. تُستخدم بعض التقنيات الرئيسية أيضًا في رمز التدريب ، بما في ذلك استخدام LORA لتصحيح المعلمة الفعالة ، باستخدام خوارزمية PPO كوسيلة لتحسين الإستراتيجية ، وتنفيذ خوارزمية GAE لحساب وظائف مفيدة ، واستخدام تشغيل أولوية لتحسين كفاءة التدريب.
تجدر الإشارة إلى أن رمز LLAMA-O1 تم نشره ضمن حساب GitHub يسمى Simpleberry. من الحسابات الأخرى ذات الصلة البسيطة ومعلومات موقع الويب الرسمي ، لا يمكن ملاحظة إلا أن طبيعتها هي مختبر أبحاث ، ولكن لا يتم الكشف عن مزيد من المعلومات حول اتجاه البحث.
بالإضافة إلى Llama-O1 ، فإن مشروع نسخة طبق الأصل من O1 المتقدم علنًا هو O1-Journey من فريق جامعة شنغهاي جياوتونج. أصدر الفريق أول تقرير للتقدم في أوائل شهر أكتوبر ، حيث قدم نموذج التعلم المبتكرة في الرحلة والنموذج الأول لدمج البحث والتعلم بنجاح في التفكير الرياضي. يتألف فريق التطوير الأساسي لـ O1-Journey بشكل أساسي من طالبة صغار وكبار في جامعة شنغهاي جياوتونج ، بالإضافة إلى طلاب الدكتوراه في السنة الأولى من مختبر Gair (مختبر أبحاث الذكاء الاصطناعي العام). في جامعة شنغهاي جياوتونج.
عنوان الورق: https://arxiv.org/pdf/2410.02884
https://arxiv.org/pdf/2406.07394
يمثل المصدر المفتوح لإصدار LLAMA O1 تقدمًا مهمًا في مجال حل المشكلات الرياضيات من الذكاء الاصطناعي ويوفر أيضًا أساسًا متينًا لمزيد من البحث والتطبيق. نتطلع إلى المزيد من الإنجازات المبتكرة بناءً على هذا المشروع في المستقبل.