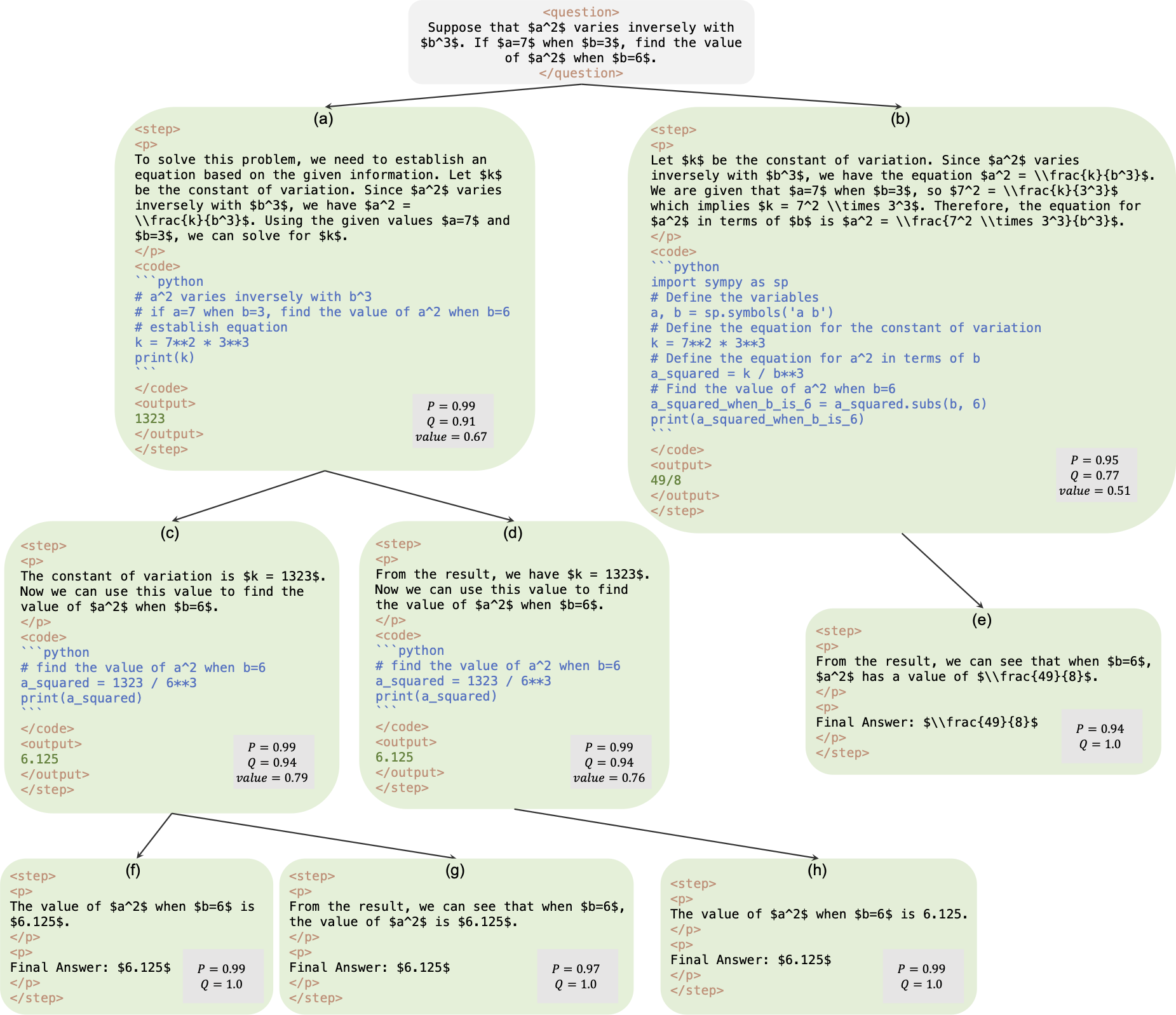
Dies ist das offizielle Repository für die Arbeit AlphaMath Almost Zero: Prozessüberwachung ohne Prozess. Der Code wird aus unserer internen Unternehmenscodebasis extrahiert. Daher kann es bei der Wiedergabe der in unserem Artikel genannten Zahlen zu geringfügigen Abweichungen kommen, die jedoch sehr nahe beieinander liegen sollten. Unser Ansatz besteht darin, die Richtlinien- und Wertemodelle ausschließlich mithilfe der mathematischen Argumentation zu trainieren, die aus dem Monte-Carlo-Tree-Search-Framework (MCTS) abgeleitet ist, wodurch GPT-4 oder menschliche Anmerkungen überflüssig werden. Dies ist eine Darstellung der von MCTS in Runde 3 generierten Trainingsinstanz.
Checkpoint : AlphaMath-7B Runde 3? / AlphaMath-7B Runde 3 ?
Datensatz : AlphaMath-Round3-Trainset? Der Lösungsprozess der Trainingsdaten wird automatisch basierend auf MCTS und Checkpoint in Runde 2 generiert. Für das Training der Richtlinien- und Wertemodelle sind sowohl positive als auch negative Beispiele enthalten.
Trainingscode : Aufgrund von Richtlinien können wir nur die Implementierungsdetails einiger Schlüsselfunktionen veröffentlichen, die grundsätzlich in Ihrem eigenen Trainingscode geändert werden sollten.
| Inferenzmethode | Genauigkeit | Durchschn. Zeit (s) pro q | Durchschn. Schritte | # Sols |
|---|---|---|---|---|
| Gierig | 53,62 | 1.6 | 3.1 | 1 |
| Maj@5 | 61,84 | 2.9 | 2.9 | 5 |
| Stufenbalken (1,5) | 62,32 | 3.1 | 3,0 | Top-1 |
| 5 Läufe + Maj@5 | 67.04 | x5 | x1 | 5 Top-1 |
| Stufenbalken (2,5) | 64,66 | 2.4 | 2.4 | Top-1 |
| Stufenbalken (3,5) | 65,74 | 2.3 | 2.2 | Top-1 |
| Stufenbalken (5,5) | 65,98 | 4.7 | 2.3 | Top-1 |
| 1 Lauf + Maj@5 | 66,54 | x1 | x1 | Top-5 |
| 5 Läufe + Maj@5 | 69,94 | x5 | x1 | 5 Top-1 |
| MCTS (N=40) | 64.02 | 10.1 | 3.8 | Top-1 |
+ Maj@5 muss also fünfmal ausgeführt werden, was die Vielfalt fördert.+ Maj@5 verwendet also direkt die 5 Kandidaten, denen es an Diversität mangelt.| Temperatur | 0,6 | 1,0 |
|---|---|---|
| Stufenbalken (1,5) | 62,32 | 62,76 |
| Stufenbalken (2,5) | 64,66 | 65,60 |
| Stufenbalken (3,5) | 65,74 | 66,28 |
| Stufenbalken (5,5) | 65,98 | 66,38 |
Bei der Strahlsuche auf Stufenebene kann die Einstellung temperature=1.0 zu etwas besseren Ergebnissen führen.
requirements.txt pip install -r requirements.txt
Oder folgen Sie einfach den cmds
> git clone https://github.com/MARIO-Math-Reasoning/Super_MARIO.git
> git clone https://github.com/MARIO-Math-Reasoning/MARIO_EVAL.git
> git clone https://github.com/MARIO-Math-Reasoning/vllm.git
> cd Super_MARIO && pip install -r requirements.txt && cd ..
> cd MARIO_EVAL/latex2sympy && pip install . && cd ..
> pip install -e .
> cd ../vllm
> pip install -e . scripts/save_value_head.py verwenden, um den Wert head zum LLM hinzuzufügen. Sie können einen der beiden folgenden Befehle ausführen. Es kann zu geringfügigen Genauigkeitsunterschieden zwischen den beiden kommen. In unserer Maschine erreichte der erste 53,4 % und der zweite 53,62 %.
python react_batch_demo.py
--custom_cfg configs/react_sft.yaml
--qaf ../MARIO_EVAL/data/math_testset_annotation.json
oder
# use step_beam (1, 1) without value func
python solver_demo.py
--custom_cfg configs/sbs_greedy.yaml
--qaf ../MARIO_EVAL/data/math_testset_annotation.json
Auf unserer Maschine im MATH-Testset kann der folgende Befehl mit der Konfiguration B1=1, B2=5 ~62 % erreichen, und der mit der Konfiguration B1=3, B2=5 kann ~65 % erreichen.
python solver_demo.py
--custom_cfg configs/sbs_sft.yaml
--qaf ../MARIO_EVAL/data/math_testset_annotation.json
Berechnen Sie die Genauigkeit
python eval_output_jsonl.py
--res_file <the saved tree jsonl file by solver_demo.py>
Die ground_truth (die endgültige Antwort, nicht der Lösungsprozess) muss in qaf JSON- oder JSONL-Datei bereitgestellt werden (Beispielformat kann sich auf ../MARIO_EVAL/data/math_testset_annotation.json beziehen).
Runde 1
# Checkpoint Initialization is required by adding value head
python solver_demo.py
--custom_cfg configs/mcts_round1.yaml
--qaf /path/to/training/data
Runde > 1, nach SFT
python solver_demo.py
--custom_cfg configs/mcts_sft_round.yaml
--qaf /path/to/training/data
Für die Lösungsgenerierung wird nur question verwendet, für die Berechnung der Genauigkeit wird jedoch „ ground_truth verwendet.
python solver_demo.py
--custom_cfg configs/mcts_sft.yaml
--qaf ../MARIO_EVAL/data/math_testset_annotation.json
Anders als bei der Strahlsuche auf Stufenebene müssen Sie zunächst einen vollständigen Baum erstellen, dann das MCTS offline ausführen und dann die Genauigkeit berechnen.
python offline_inference.py
--custom_cfg configs/offline_inference.yaml
--tree_jsonl <the saved tree jsonl file by solver_demo.py>
Hinweis: Dieses Auswertungsskript kann auch mit der gespeicherten Baum-auf-Schritt-Strahlensuche ausgeführt werden, und die Genauigkeit sollte gleich bleiben.
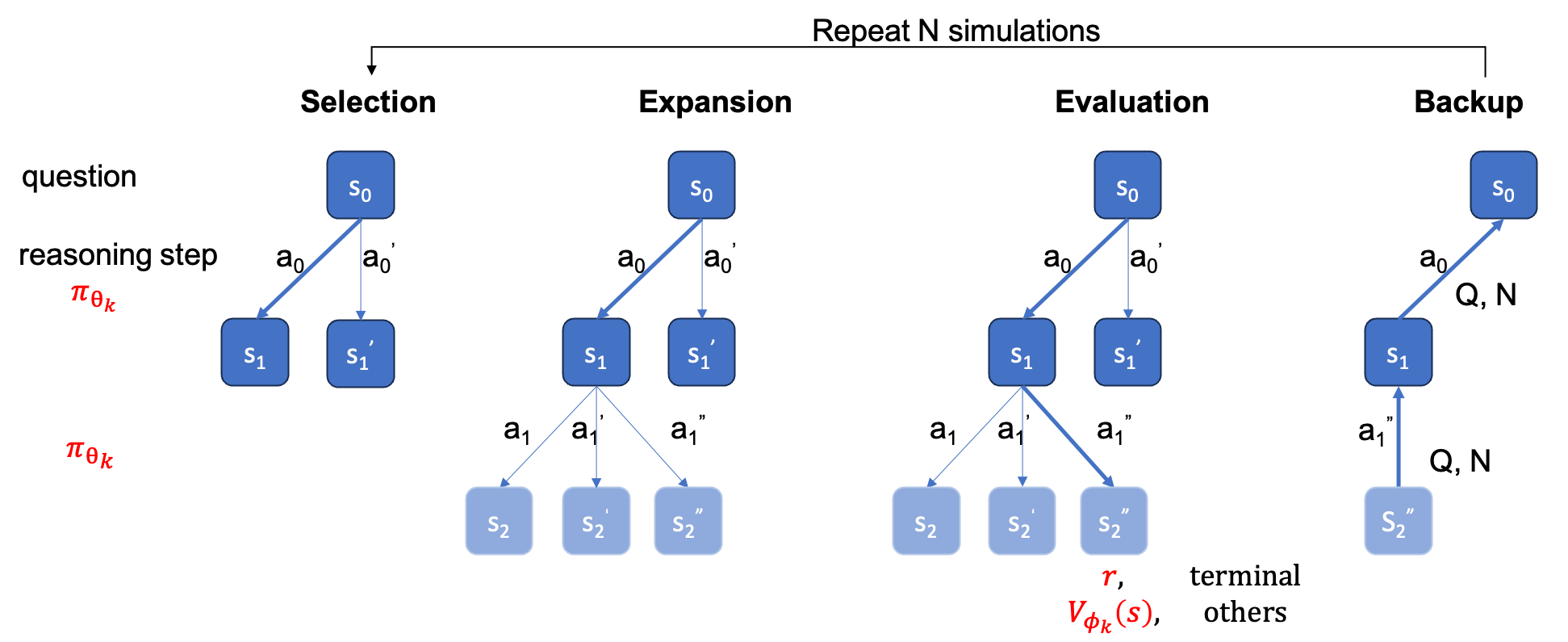
Da die Grundwahrheit für Trainingsdaten bekannt ist, ist der Wert des letzten Schritts die Belohnung und der Q-Wert kann sehr gut konvergieren.
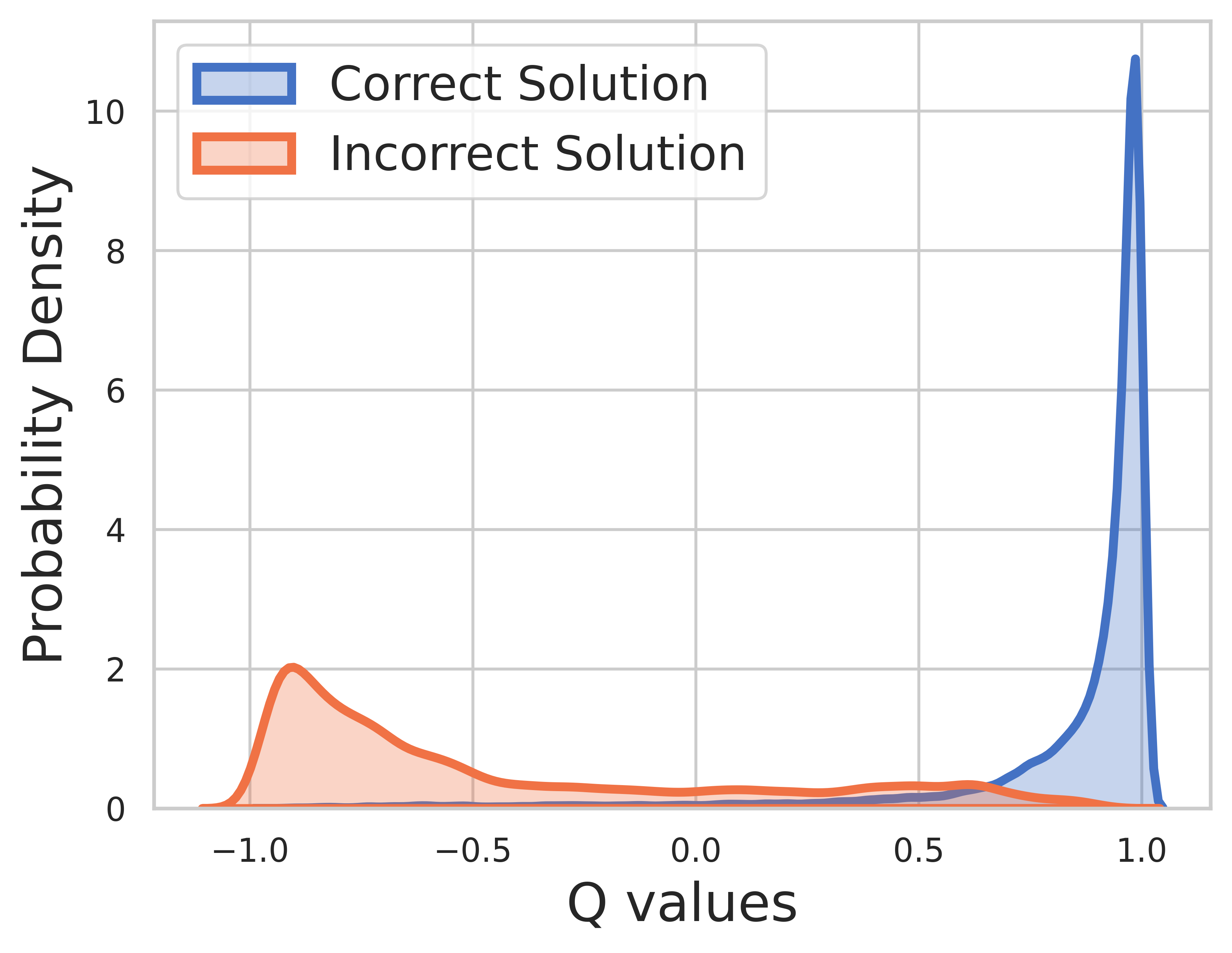
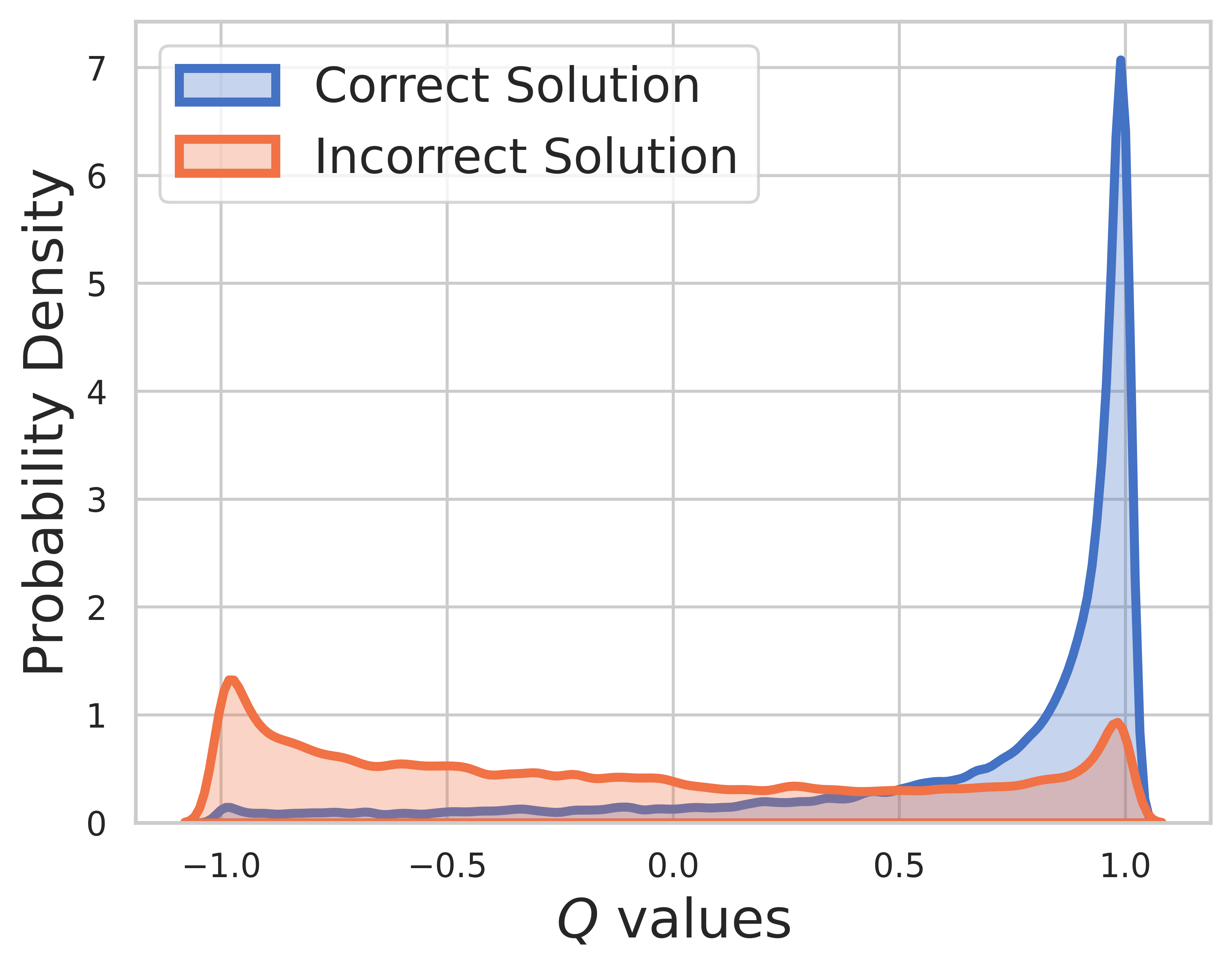
Beim Testsatz ist die Grundwahrheit unbekannt, daher umfasst die Q-Wert-Verteilung sowohl Zwischen- als auch Endschritte. Aus dieser Zahl können wir herausfinden
SVPO von MCTS
@misc{chen2024steplevelvaluepreferenceoptimization,
title={Step-level Value Preference Optimization for Mathematical Reasoning},
author={Guoxin Chen and Minpeng Liao and Chengxi Li and Kai Fan},
year={2024},
eprint={2406.10858},
archivePrefix={arXiv},
primaryClass={cs.CL},
url={https://arxiv.org/abs/2406.10858},
}
MCTS-Version
@misc{chen2024alphamathzeroprocesssupervision,
title={AlphaMath Almost Zero: process Supervision without process},
author={Guoxin Chen and Minpeng Liao and Chengxi Li and Kai Fan},
year={2024},
eprint={2405.03553},
archivePrefix={arXiv},
primaryClass={cs.CL},
url={https://arxiv.org/abs/2405.03553},
}
Bewertungstoolkit
@misc{zhang2024marioevalevaluatemath,
title={MARIO Eval: Evaluate Your Math LLM with your Math LLM--A mathematical dataset evaluation toolkit},
author={Boning Zhang and Chengxi Li and Kai Fan},
year={2024},
eprint={2404.13925},
archivePrefix={arXiv},
primaryClass={cs.CL},
url={https://arxiv.org/abs/2404.13925},
}
OVM-Version (Outcome Value Model).
@misc{liao2024mariomathreasoningcode,
title={MARIO: MAth Reasoning with code Interpreter Output -- A Reproducible Pipeline},
author={Minpeng Liao and Wei Luo and Chengxi Li and Jing Wu and Kai Fan},
year={2024},
eprint={2401.08190},
archivePrefix={arXiv},
primaryClass={cs.CL},
url={https://arxiv.org/abs/2401.08190},
}