Lanczos (ausgesprochen Lanchos) Resampling ist eine hochentwickelte Technik zur Interpolation digitaler Signale, die im Vergleich zu einfacheren Methoden wie der nächsten Nachbarn und der bilinearen Interpolation eine bessere Bildqualität bietet. Durch die effektive Beibehaltung von Details und die Minimierung von Aliasing-Artefakten wird Lanczos Resampling häufig in Bild- und Signalverarbeitungsanwendungen eingesetzt.
Lanczos zeichnet sich zwar durch eine hervorragende Bildqualität aus, allerdings geht dies mit einer erhöhten Rechenkomplexität einher. Darüber hinaus kann die Möglichkeit von „klingelnden“ Artefakten, insbesondere an scharfen Kanten, ein Nachteil sein. Trotz dieser Herausforderungen bleibt Lanczos aufgrund seiner Gesamtleistungsvorteile die bevorzugte Wahl für Aufgaben wie Bildskalierung und -drehung.
Dieses Dokument bietet einen umfassenden Überblick über das Lanczos-Resampling, einschließlich seiner theoretischen Grundlagen, Implementierungsdetails und praktischen Anwendungen. Es dient als wertvolle Ressource für Entwickler und Forscher, die diese leistungsstarke Technik verstehen und nutzen möchten. Die folgenden Abschnitte befassen sich mit wichtigen Aspekten des Lanczos-Resamplings, wie dem Lanczos-Kernel, Interpolations- und Resampling-Prozessen, Flusserhaltung, Upsampling, Downsampling, Sample-Positionierung, Ausgabebereich, mehrdimensionale Interpolation und Trennbarkeit. Ein praktisches Beispiel mit zugehörigem Quellcode ist enthalten.
Der Lanczos-Kernel, der für eine bestimmte Unterstützungsgröße definiert ist, ist eine Funktion, die beim Lanczos-Resampling verwendet wird. Der Kernel ist definiert als:
L(x) = sinc(x)*sinc(x/a) : -a < x < a
= 0.0 : otherwise
Wo:
Die normalisierte Sinc-Funktion ist definiert als:
sinc(x) = 1.0 : x = 0.0
= sin(PI*x)/(PI*x) : otherwise
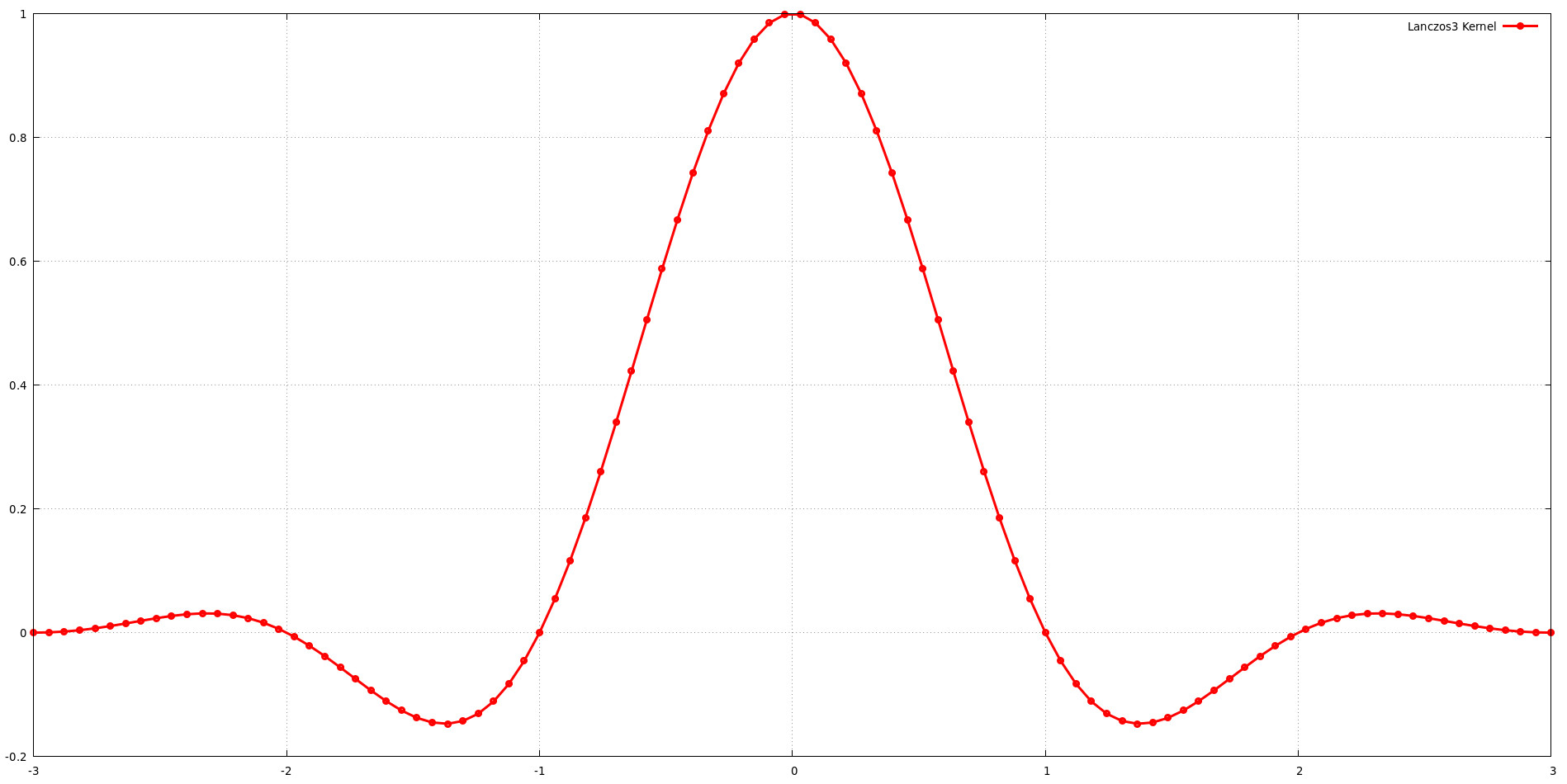
Die Grafik veranschaulicht die Form des Lanczos-Kernels für eine Unterstützungsgröße von a = 3. Dies bedeutet, dass der Kernel drei Lappen der Sinc-Funktion enthält. Während eine Vergrößerung der Unterstützungsgröße (a) im Allgemeinen mehr Flexibilität bei der Gestaltung des Frequenzgangs bietet, erhöht sie auch den Rechenaufwand. Bei der Wahl der Trägergröße muss ein Gleichgewicht zwischen Bildqualität und Recheneffizienz gefunden werden. Jim Blinns Feststellung, dass der Lanczos-Kernel mit a = 3 ein hervorragendes Gleichgewicht zwischen Niederfrequenzerhaltung und Hochfrequenzunterdrückung bietet, stützt diese Annahme.
Hinweis: Die Begriffe „Kernelbreite“, „Unterstützungsgröße“ und „Filtergröße“ werden häufig synonym zur Beschreibung des Parameters a verwendet. Im Zusammenhang mit Lanczos Resampling spiegelt „Unterstützungsgröße“ das Konzept jedoch am genauesten wider.
Die Lanczos-Interpolation ist eine Technik, mit der ein diskretes Signal auf eine neue Abtastrate umgetastet wird. Dies wird erreicht, indem das Originalsignal mit einem Lanczos-Kernel gefaltet wird.
Das interpolierte Signal s2(x) lässt sich wie folgt berechnen:
s2(x) = (1/w(x))*
SUM(i = -a + 1, i = a,
s1(floor(x) + i)*
L(i - x + floor(x)))
Wo:
Flussmittel erhalten:
Der Normalisierungsfaktor w(x) ist entscheidend für den Erhalt der Gesamtsignalenergie oder -masse während des Interpolationsprozesses. Dadurch wird sichergestellt, dass die Summe der interpolierten Werte annähernd der Summe der ursprünglichen Stichproben entspricht. Das Filtergewicht wird wie folgt berechnet:
w(x) = SUM(i = -a + 1, i = a, L(i - x + floor(x)))
Upsampling:
Bei Erhöhung der Abtastrate kann die Lanczos-Interpolationsgleichung ohne Modifikationen direkt verwendet werden.
Downsampling:
Um Aliasing-Artefakte beim Verringern der Abtastrate zu vermeiden, muss die Filterskala an die neue Abtastrate angepasst werden.
fs = n1/n2
s2(x) = (1/w(x))*
SUM(i = -(fs*a) + 1, i = (fs*a),
s1(floor(x) + i)*
L((i - x + floor(x))/fs))
Wo:
Beim Resampling eines Signals von n1 Samples auf n2 Samples werden die folgenden Sample-Positionen verwendet. Der Index j wird verwendet, um die Abtastwerte aus dem abgetasteten Signal s2(x) darzustellen. Der Term (j + 0,5) ist der Mittelpunkt einer Stichprobe in s2(x). Der Schritt skaliert einen Punkt in s2(x) auf einen Punkt in s1(x). Der letzte Term von -0,5 in x ist eine Phasenverschiebung, die dazu führt, dass die Stichproben des Lanczos-Koeffizienten versetzt werden.
step = n1/n2
j = [0..n2)
x = (j + 0.5)*step - 0.5
Bei der Lanczos-Interpolation muss besonders auf die Signalgrenzen geachtet werden. Zu den gängigen Kantenbearbeitungstechniken gehören:
Nullpolsterung:
s1(x) = s1[floor(x)] : x = [0, n1)
= 0.0 : otherwise
Klemmung:
s1(x) = s1[clamp(floor(x), 0, n1 - 1)]
Das Klemmen wird oft bevorzugt, da es Kantenartefakte reduziert, die durch scharfe Diskontinuitäten in der Nähe der Kanten verursacht werden. Die Wahl der Kantenbearbeitungsmethode hängt jedoch von der spezifischen Anwendung und der gewünschten Leistung ab.
Der Bereich von s2(x) kann aufgrund der Lappen von L(x) größer sein als der von s1(x). Beispielsweise muss ein Eingangssignal s1(x), das Pixelfarben im Bereich von [0,0,1,0] entspricht, auf denselben Bereich begrenzt werden, um sicherzustellen, dass die Ausgangswerte bei der Rückkonvertierung in vorzeichenlose Bytes von [0,255] nicht überlaufen. .
Der Lanczos-Kernel kann auf mehrere Dimensionen erweitert werden, um eine Interpolation an Bildern oder höherdimensionalen Daten durchzuführen.
Der zweidimensionale Lanczos-Kernel ist definiert als:
L(x, y) = sinc(sqrt(x^2 + y^2))*sinc(sqrt(x^2 + y^2)/a)
Das interpolierte Signal s2(x, y) lässt sich nach folgender Formel berechnen:
s2(x, y) = (1/w(x, y))*
SUM(i = -a + 1, i = a,
SUM(j = -a + 1, j = a,
s1(floor(x) + j, floor(y) + i)*
L(j - x + floor(x), i - y + floor(y))))
Wobei w(x, y) der mithilfe des zweidimensionalen Lanczos-Kernels berechnete Normalisierungsfaktor ist.
Im Gegensatz zu einigen Interpolationsmethoden ist der Lanczos-Kernel nicht trennbar, was bedeutet, dass er nicht in das Produkt eindimensionaler Kerne einbezogen werden kann. Diese Eigenschaft führt im Allgemeinen zu höheren Rechenkosten im Vergleich zu trennbaren Kerneln. Um die Leistung zu verbessern, nähern sich einige Implementierungen dem Lanczos-Kernel an, indem sie separate Durchgänge für die horizontale und vertikale Dimension durchführen.
Horizontale Interpolation:
Vertikale Interpolation:
Mathematische Darstellung:
s2(x, y) = (1/w(x))*
SUM(j = -a + 1, j = a,
s1(floor(x) + j, y)*
L(j - x + floor(x)))
s3(x, y) = (1/w(y))*
SUM(i = -a + 1, i = a,
s2(x, floor(y) + i)*
L(i - y + floor(y)))
Beachten Sie, dass die Normalisierungsfaktoren w(x) und w(y) mithilfe des eindimensionalen Lanczos-Kernels berechnet werden.
Wichtige Punkte:
Ebenso kann das mehrmalige rekursive Resampling eines Signals, wie es üblicherweise zum Generieren von Textur-Mipmaps durchgeführt wird, die Bildqualität aufgrund der Anhäufung von Fehlern bei jedem Resampling-Schritt verschlechtern.
Führen Sie das Lancos-Test-Beispiel aus und verwenden Sie Gnuplot, um zu sehen, wie sich Lanczos Resampling auf ein einfaches eindimensionales Signal auswirkt, wenn es um den Faktor 2 hoch- und heruntergerechnet wird.
make
./lanczos-test
gnuplot
> load "output.plot"
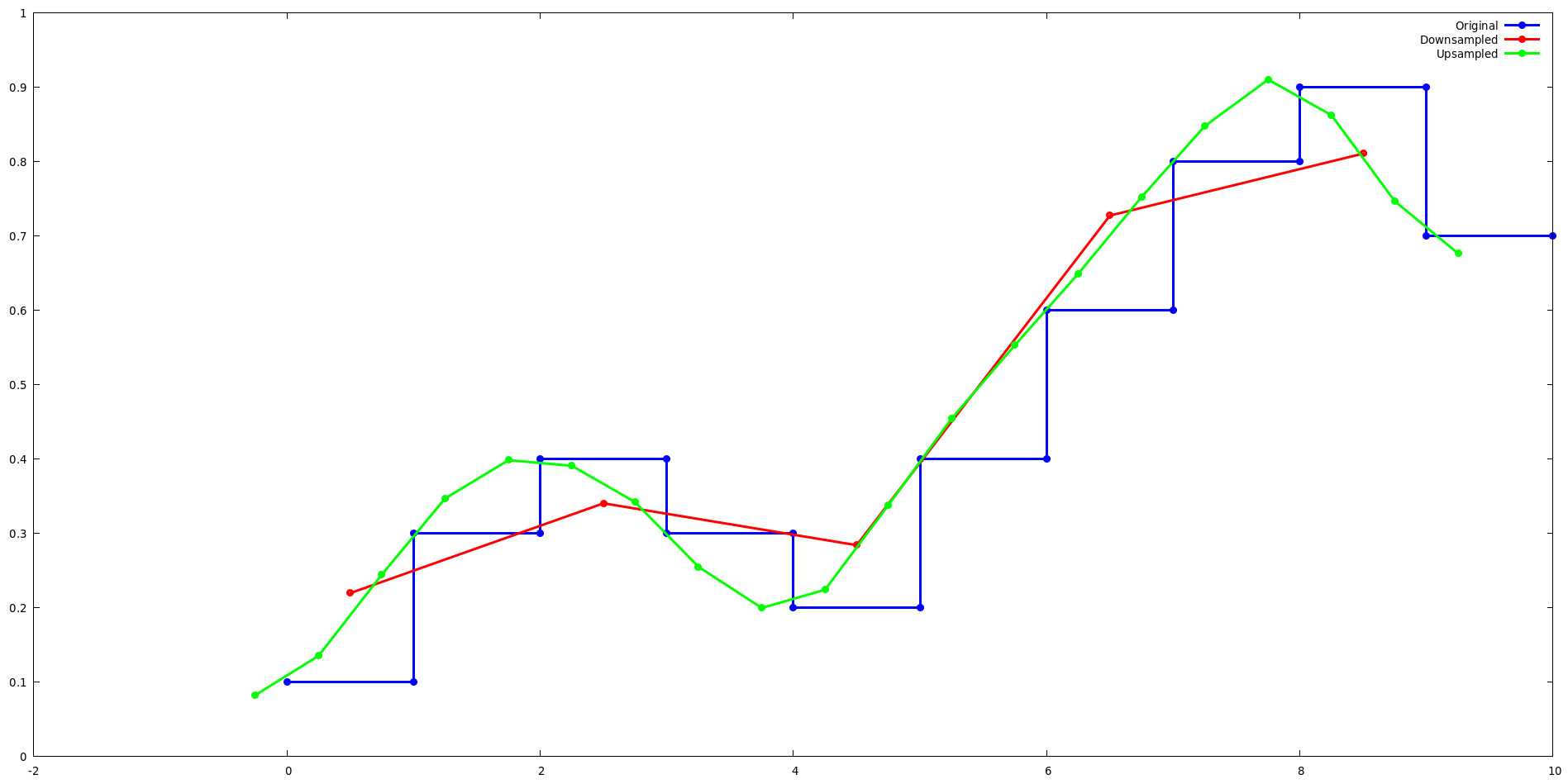
Upsampling:
Beim Upsampling um eine Zweierpotenz wechselt der Lanczos-Kernel zwischen Wertesätzen auf 2^Ebene. Betrachten Sie beispielsweise die ersten vier Ausgaben des Lanzcos-Test-Upsample-Beispiels. Beachten Sie, dass sich die Ausgaben für L(x) für j={0,2} und j={1,3} wiederholen.
upsample n1=10, n2=20
j=0, x=-0.250000
i=-2, L(-2.750000)=0.007356, S1(-3.000000)=0.100000
i=-1, L(-1.750000)=-0.067791, S1(-2.000000)=0.100000
i=0, L(-0.750000)=0.270190, S1(-1.000000)=0.100000
i=1, L(0.250000)=0.890067, S1(0.000000)=0.100000
i=2, L(1.250000)=-0.132871, S1(1.000000)=0.300000
i=3, L(2.250000)=0.030021, S1(2.000000)=0.400000
s2=0.082129, s2/w=0.082379, w=0.996972
j=1, x=0.250000
i=-2, L(-2.250000)=0.030021, S1(-2.000000)=0.100000
i=-1, L(-1.250000)=-0.132871, S1(-1.000000)=0.100000
i=0, L(-0.250000)=0.890067, S1(0.000000)=0.100000
i=1, L(0.750000)=0.270190, S1(1.000000)=0.300000
i=2, L(1.750000)=-0.067791, S1(2.000000)=0.400000
i=3, L(2.750000)=0.007356, S1(3.000000)=0.300000
s2=0.134869, s2/w=0.135279, w=0.996972
j=2, x=0.750000
i=-2, L(-2.750000)=0.007356, S1(-2.000000)=0.100000
i=-1, L(-1.750000)=-0.067791, S1(-1.000000)=0.100000
i=0, L(-0.750000)=0.270190, S1(0.000000)=0.100000
i=1, L(0.250000)=0.890067, S1(1.000000)=0.300000
i=2, L(1.250000)=-0.132871, S1(2.000000)=0.400000
i=3, L(2.250000)=0.030021, S1(3.000000)=0.300000
s2=0.243853, s2/w=0.244594, w=0.996972
j=3, x=1.250000
i=-2, L(-2.250000)=0.030021, S1(-1.000000)=0.100000
i=-1, L(-1.250000)=-0.132871, S1(0.000000)=0.100000
i=0, L(-0.250000)=0.890067, S1(1.000000)=0.300000
i=1, L(0.750000)=0.270190, S1(2.000000)=0.400000
i=2, L(1.750000)=-0.067791, S1(3.000000)=0.300000
i=3, L(2.750000)=0.007356, S1(4.000000)=0.200000
s2=0.345945, s2/w=0.346996, w=0.996972
Downsampling:
Beim Downsampling um eine Zweierpotenz wird der Lanczos-Kernel unabhängig von x, da (x – floor(x)) zu einer Konstante wird, die der Phasenverschiebung entspricht. Betrachten Sie beispielsweise die ersten beiden Ausgaben des Downsample-Beispiels „lanzcos-test“. Beachten Sie, dass sich die Ausgaben von L(x) für jedes j wiederholen.
downsample n1=10, n2=5
j=0, x=0.500000
i=-5, L(-2.750000)=0.007356, S1(-5.000000)=0.100000
i=-4, L(-2.250000)=0.030021, S1(-4.000000)=0.100000
i=-3, L(-1.750000)=-0.067791, S1(-3.000000)=0.100000
i=-2, L(-1.250000)=-0.132871, S1(-2.000000)=0.100000
i=-1, L(-0.750000)=0.270190, S1(-1.000000)=0.100000
i=0, L(-0.250000)=0.890067, S1(0.000000)=0.100000
i=1, L(0.250000)=0.890067, S1(1.000000)=0.300000
i=2, L(0.750000)=0.270190, S1(2.000000)=0.400000
i=3, L(1.250000)=-0.132871, S1(3.000000)=0.300000
i=4, L(1.750000)=-0.067791, S1(4.000000)=0.200000
i=5, L(2.250000)=0.030021, S1(5.000000)=0.400000
i=6, L(2.750000)=0.007356, S1(6.000000)=0.600000
s2=0.437796, s2/w=0.219563, w=1.993943
j=1, x=2.500000
i=-5, L(-2.750000)=0.007356, S1(-3.000000)=0.100000
i=-4, L(-2.250000)=0.030021, S1(-2.000000)=0.100000
i=-3, L(-1.750000)=-0.067791, S1(-1.000000)=0.100000
i=-2, L(-1.250000)=-0.132871, S1(0.000000)=0.100000
i=-1, L(-0.750000)=0.270190, S1(1.000000)=0.300000
i=0, L(-0.250000)=0.890067, S1(2.000000)=0.400000
i=1, L(0.250000)=0.890067, S1(3.000000)=0.300000
i=2, L(0.750000)=0.270190, S1(4.000000)=0.200000
i=3, L(1.250000)=-0.132871, S1(5.000000)=0.400000
i=4, L(1.750000)=-0.067791, S1(6.000000)=0.600000
i=5, L(2.250000)=0.030021, S1(7.000000)=0.800000
i=6, L(2.750000)=0.007356, S1(8.000000)=0.900000
s2=0.678627, s2/w=0.340344, w=1.993943
Als weitere Optimierung kann der Lanczos-Kernel für diese Fälle vorberechnet werden, um die teure Sinc-Funktionsberechnung zu eliminieren.
Diese README-Datei wurde mit Unterstützung von Google Gemini erstellt.
Weitere Referenzen sind:
Dieser Code wurde von Jeff Boody unter der MIT-Lizenz implementiert.
Copyright (c) 2024 Jeff Boody
Permission is hereby granted, free of charge, to any person obtaining a
copy of this software and associated documentation files (the "Software"),
to deal in the Software without restriction, including without limitation
the rights to use, copy, modify, merge, publish, distribute, sublicense,
and/or sell copies of the Software, and to permit persons to whom the
Software is furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included
in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN
THE SOFTWARE.