Greedy Gaussian Segmentation (GGS) ist ein Python-Löser zur effizienten Segmentierung multivariater Zeitreihendaten. Einzelheiten zur Implementierung finden Sie in unserem Dokument unter http://stanford.edu/~boyd/papers/ggs.html.
Der GGS-Solver nimmt eine n-mal-T-Datenmatrix und zerlegt die T-Zeitstempel auf einem n-dimensionalen Vektor in Segmente, über die die Daten als unabhängige Stichproben aus einer multivariaten Gaußverteilung gut erklärt werden können. Dazu wird ein kovarianzreguliertes Maximum-Likelihood-Problem formuliert und mithilfe einer Greedy-Heuristik gelöst. Die vollständigen Einzelheiten werden im Artikel beschrieben.
git clone [email protected]:davidhallac/GGS.git
cd GGS
python helloworld.py
ggs.py im selben Verzeichnis wie Ihre neue Datei befindet, und fügen Sie dann den folgenden Code am Anfang Ihres Skripts hinzu: from ggs import *
Das GGS-Paket hat drei Hauptfunktionen:
bps, objectives = GGS(data, Kmax, lamb)
Findet K Haltepunkte in den Daten für einen bestimmten Regularisierungsparameter Lambda
Eingaben
Daten – eine n-mal-T-Datenmatrix mit T Zeitstempeln eines n-dimensionalen Vektors
Kmax – die Anzahl der zu findenden Haltepunkte
lamb – Regularisierungsparameter für die regulierte Kovarianz
Rückgaben
bps – Liste von Listen, wobei Element i der größeren Liste die Menge der Haltepunkte ist, die bei K = i im GGS-Algorithmus gefunden werden
Ziele – Liste der Zielwerte bei jedem Zwischenschritt (für K = 0 bis Kmax)
meancovs = GGSMeanCov(data, breakpoints, lamb)
Ermittelt die Mittelwerte und regulierten Kovarianzen jedes Segments anhand einer Reihe von Haltepunkten.
Eingaben
Daten – eine n-mal-T-Datenmatrix mit T Zeitstempeln eines n-dimensionalen Vektors
Haltepunkte – eine Liste der Haltepunktpositionen
lamb – Regularisierungsparameter für die regulierte Kovarianz
Rückgaben
meancovs – eine Liste von (Mittelwert, Kovarianz)-Tupeln für jedes Segment in den Daten
cvResults = GGSCrossVal(data, Kmax=25, lambList = [0.1, 1, 10])
Führt eine 10-fache Kreuzvalidierung durch und gibt die Zug- und Testsatzwahrscheinlichkeit für jedes (K, Lambda)-Paar bis zu Kmax zurück
Eingaben
Daten – eine n-mal-T-Datenmatrix mit T Zeitstempeln eines n-dimensionalen Vektors
Kmax – die maximale Anzahl von Haltepunkten, auf denen GGS ausgeführt werden soll
lambList – eine Liste der zu testenden Regularisierungsparameter
Rückgaben
cvResults – Liste von (lamb, ([TrainLL],[TestLL])) Tupeln für jeden Regularisierungsparameter in lambList. Hier sind TrainLL und TestLL die durchschnittliche Log-Likelihood pro Stichprobe über die 10-fache Kreuzvalidierung für alle K von 0 bis Kmax
Zusätzliche optionale Parameter (für alle drei oben genannten Funktionen):
Features = [] – Wählen Sie eine bestimmte Teilmenge von Spalten in den Daten aus, die bearbeitet werden sollen
verbose = False – Gibt Zwischenschritte aus, wenn der Algorithmus ausgeführt wird
Wenn Sie financeExample.py ausführen, erhalten Sie das folgende Diagramm, das das Ziel (Gleichung 4 im Dokument) im Verhältnis zur Anzahl der Haltepunkte zeigt:
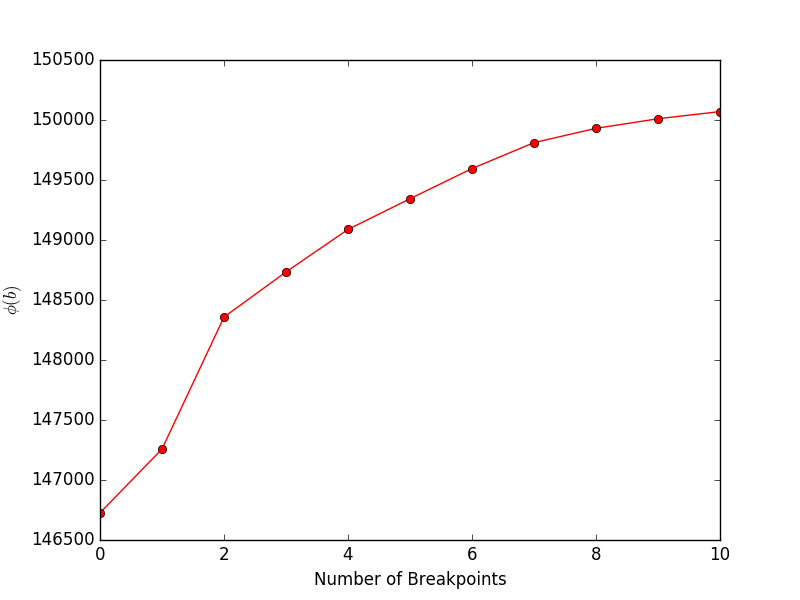
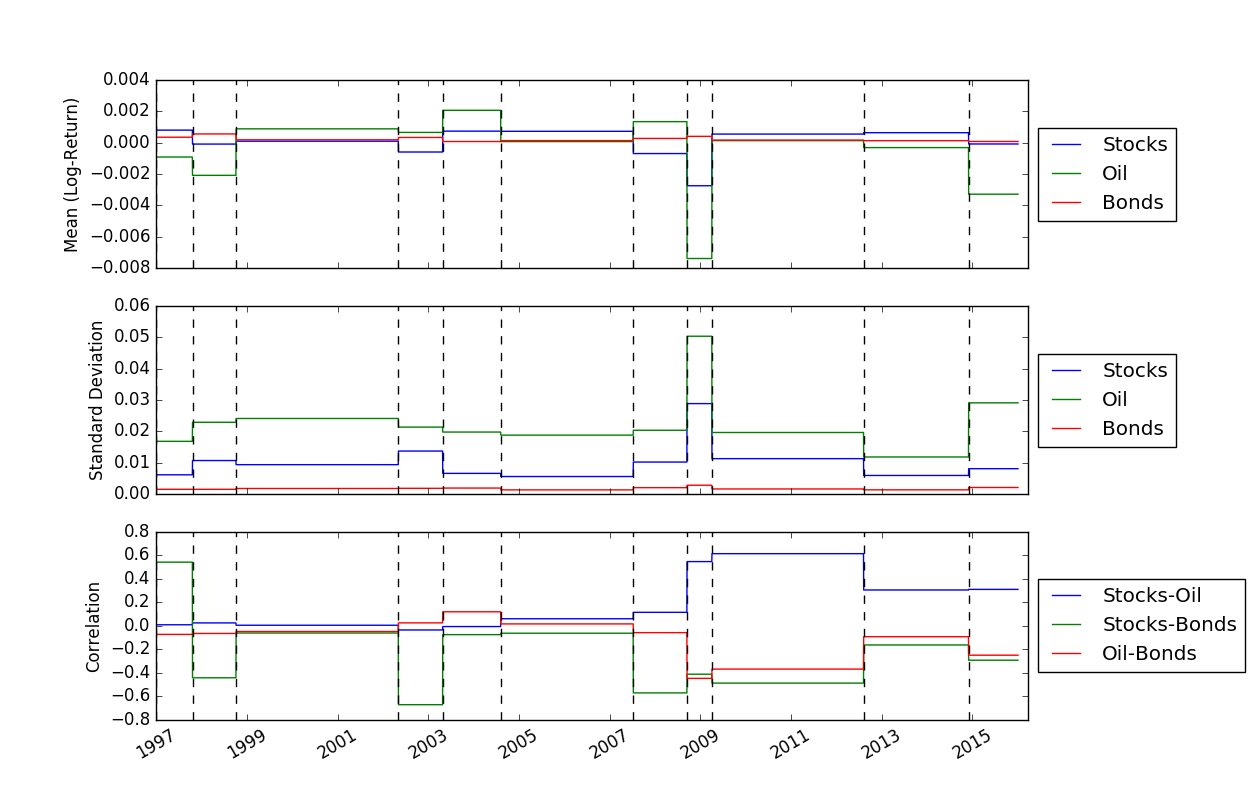
Sobald wir die Positionen der Haltepunkte ermittelt haben, können wir die Funktion FindMeanCovs() verwenden, um die Mittelwerte und Kovarianzen jedes Segments zu ermitteln. Im Beispiel in helloworld.py ergibt das Plotten der Mittelwerte, Varianzen und Kovarianzen der drei Signale:
Um eine Kreuzvalidierung durchzuführen, die bei der Bestimmung optimaler Werte von K und Lambda nützlich sein kann, können wir den folgenden Code verwenden, um die Daten zu laden, die Kreuzvalidierung durchzuführen und dann die Test- und Trainingswahrscheinlichkeit grafisch darzustellen:
from ggs import *
import numpy as np
import matplotlib.pyplot as plt
filename = "Returns.txt"
data = np.genfromtxt(filename,delimiter=' ')
feats = [0,3,7]
#Run cross-validaton up to Kmax = 30, at lambda = 1e-4
maxBreaks = 30
lls = GGSCrossVal(data, Kmax=maxBreaks, lambList = [1e-4], features = feats, verbose = False)
trainLikelihood = lls[0][1][0]
testLikelihood = lls[0][1][1]
plt.plot(range(maxBreaks+1), testLikelihood)
plt.plot(range(maxBreaks+1), trainLikelihood)
plt.legend(['Test LL','Train LL'], loc='best')
plt.show()
Die resultierende Handlung sieht folgendermaßen aus:
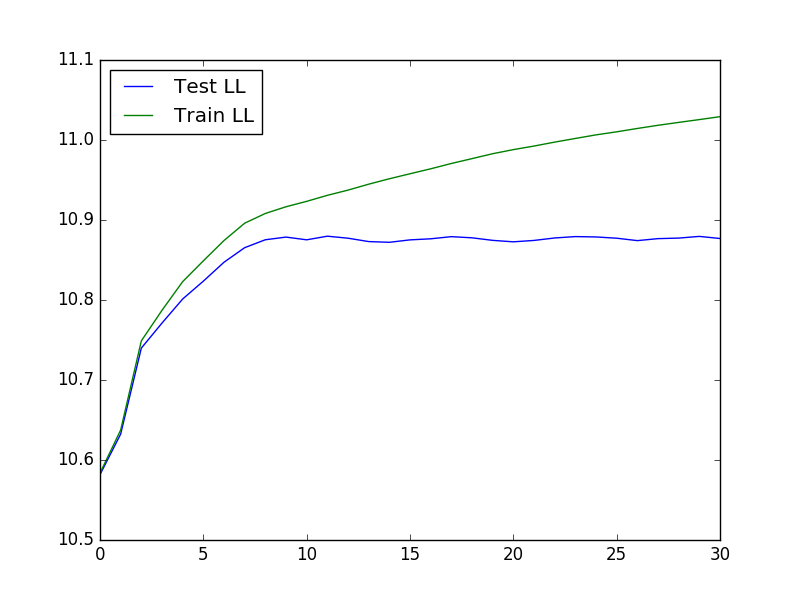
Gierige Gaußsche Segmentierung von Zeitreihendaten – D. Hallac, P. Nystrup und S. Boyd
David Hallac, Peter Nystrup und Stephen Boyd.