Bosonic ist eine Bibliothek, die für die Simulation photonischer Systeme entwickelt wurde, deren Eingaben nicht unterscheidbare Bosonen (im Interesse der Autoren Photonen) sind. Der Schwerpunkt liegt insbesondere auf der schnellen Berechnung der Mehrteilchen-Transferfunktionen für diese Systeme und unterstützt die Berechnung des Gradienten einer Kostenfunktion in Bezug auf die Systemparameter. Es wurde ursprünglich für die Entwicklung unserer quantenoptischen neuronalen Netze [1] entwickelt und enthält spezielle Funktionen für deren Simulation und Optimierung.
Die Schwerpunkte dieser Bibliothek waren zweierlei:
Die Hauptmotivation für dieses Paket war die schnelle Berechnung der Mehrteilchen-Unitärtransformation als Funktion der Einzelteilchen-Unitärtransformation und der Anzahl bosonischer Eingaben. Das heißt, wenn wir ein vierdimensionales einheitliches U haben und wissen, dass am Eingang drei Photonen vorhanden sind, möchten wir die Transformation über das wissen
Dies wird durch die Funktion bosonic.aa_phi unterstützt, die nach Aaronson und Arkhipov benannt ist, die in [2] die Form dieser Funktion angegeben haben, die wir als ihre Φ(U)-Funktion verwenden. Beispielsweise können wir den berühmten Hong-Ou-Mandel-Effekt mit einem Strahlteiler demonstrieren:
>> > import bosonic as b
>> > import numpy as np
>> > U = np . array ([[ 1 , 1 ], [ 1 , - 1 ]], dtype = complex ) / np . sqrt ( 2 )
>> > phiU = b . aa_phi ( U , 2 )
>> > print ( phiU )
[[ 0.5 + 0.j 0.70710678 + 0.j 0.5 + 0.j ]
[ 0.70710678 + 0.j 0. + 0.j - 0.70710678 + 0.j ]
[ 0.5 + 0.j - 0.70710678 + 0.j 0.5 + 0.j ]]
>> > print ( b . fock . basis ( 2 , 2 ))
[[ 2 , 0 ], [ 1 , 1 ], [ 0 , 2 ]]
>> > input = np . array ([[ 0 ], [ 1 ], [ 0 ]], dtype = complex )
>> > phiU = b . aa_phi ( U , 2 )
>> > print ( phiU . dot ( input ))
[[ 0.70710678 + 0.j ]
[ 0. + 0.j ]
[ - 0.70710678 + 0.j ]]
>> > print ( np . abs ( phiU . dot ( input )) ** 2 )
[[ 0.5 ]
[ 0. ]
[ 0.5 ]]Hier erstellen wir die Einheit, die einem 50/50-Strahlteiler in U entspricht. Wie die Zeile nach dem Drucken von phiU zeigt, ist die Basis hier [2, 0], [1, 1] und [0, 2]. Der Zustand, der einem Photoneneinfall an jedem der Eingänge entspricht, ist also [0, 1, 0]. In der letzten Zeile, zwei Zeilen, sehen wir, dass der Ausgang eine gleichmäßige Überlagerung von zwei Photonen an einem Ausgang und zwei Photonen am anderen ist, ohne dass die Wahrscheinlichkeit besteht, dass die Photonen den Ausgang über unterschiedliche Ports verlassen.
Wie in [1] beschrieben, haben wir eine vorgeschlagene Architektur für quantenoptische neuronale Netze entwickelt, die die Kachelung beliebiger einheitlicher Transformationen mit Single-Site-Nichtlinearitäten beinhaltet. Weitere Einzelheiten finden Sie im Dokument, aber hier ist eine visuelle Zusammenfassung der Architektur:
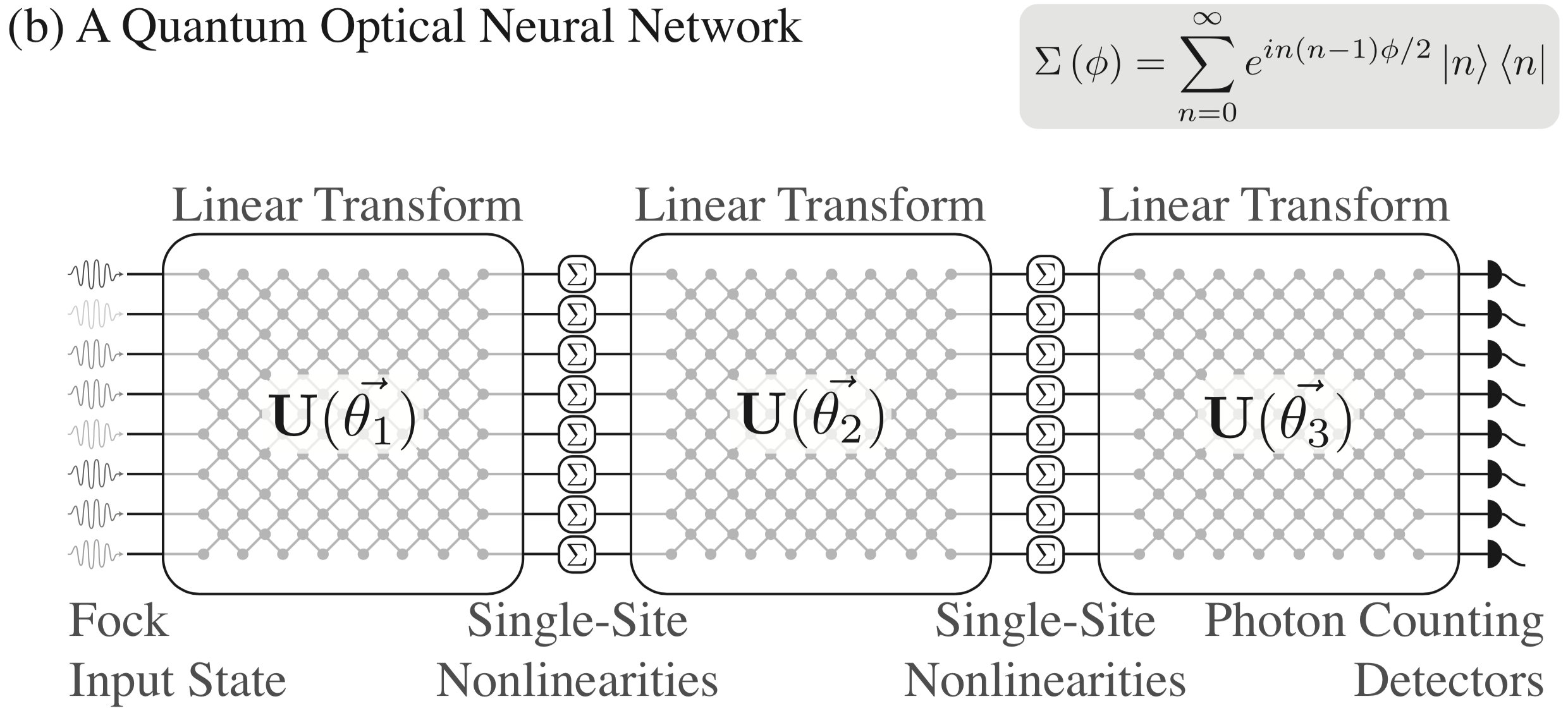
Das Klonen dieses Repositorys ist derzeit die einzige Möglichkeit, bosonic auf Ihr System zu übertragen. Zuvor muss das Python-Paket Cython installiert sein, um bosonic ordnungsgemäß zu erstellen. So etwas sollte unter Linux funktionieren (bei Bedarf mit Ihrem bevorzugten Python-Paketmanager anstelle von pip ):
$ pip install Cython
$ git clone [email protected]:steinbrecher/bosonic.git
$ cd bosonic
$ pip install .Auf dem Mac benötigen Sie außerdem gcc von Homebrew und libopenmp:
$ brew install gcc
$ brew install libomp
$ pip install Cython
$ git clone [email protected]:steinbrecher/bosonic.git
$ cd bosonic
$ CC=gcc-8 pip install . Sie sollten dann in der Lage sein, durch Ausführen zu testen, ob bosonic korrekt installiert ist
$ python setup.py test[1] Steinbrecher, GR, Olson, JP, Englund, D. & Carolan, J. (2018). Quantenoptische neuronale Netze. arXiv-Vorabdruck arXiv:1808.10047. https://arxiv.org/abs/1808.10047
[2] Aaronson, Scott und Alex Arkhipov. „Die rechnerische Komplexität der linearen Optik.“ Vorträge des dreiundvierzigsten jährlichen ACM-Symposiums zur Computertheorie. ACM, 2011. https://arxiv.org/pdf/1011.3245.pdf