greta.gam: Verallgemeinerte additive Modelle in Greta unter Verwendung von mgcv

Mit greta.gam können Sie die glatteren Funktionen und Formelsyntax von mgcv verwenden, um glatte Begriffe für die Verwendung in einem Greta-Modell zu definieren. Anschließend können Sie Ihre eigene Wahrscheinlichkeit für die Vervollständigung des Modells definieren und es von MCMC anpassen.

Dies ist in Arbeit!

Beispiel

Hier ist ein einfaches Beispiel aus der mgcv ?gam Hilfedatei:

In mgcv :

Gu & Wahba 4 term additive model # fit a model using gam() b <- gam(y ~ s(x2), data = dat)">

library( mgcv )
# > Loading required package: nlme
# > This is mgcv 1.9-1. For overview type 'help("mgcv-package")'.
set.seed( 2 )

# simulate some data...
dat <- gamSim( 1 , n = 400 , dist = " normal " , scale = 0.3 )
# > Gu & Wahba 4 term additive model

# fit a model using gam()
b <- gam( y ~ s( x2 ), data = dat )

Jetzt passt das gleiche Modell in greta :

NULL # plot the data points(dat$x2, dat$y, pch = 19, cex = 0.2)">

library( greta.gam )
# > Loading required package: greta
# > 
# > Attaching package: 'greta'
# > The following objects are masked from 'package:stats':
# > 
# >     binomial, cov2cor, poisson
# > The following objects are masked from 'package:base':
# > 
# >     %*%, apply, backsolve, beta, chol2inv, colMeans, colSums, diag,
# >     eigen, forwardsolve, gamma, identity, rowMeans, rowSums, sweep,
# >     tapply
set.seed( 2024 - 02 - 09 )
# setup the linear predictor for the smooth
z <- smooths( ~ s( x2 ), data = dat )
# > ℹ Initialising python and checking dependencies, this may take a moment.
# > ✔ Initialising python and checking dependencies ... done!               

# set the distribution of the response
distribution( dat $ y ) <- normal( z , 1 )

# make some prediction data
pred_dat <- data.frame ( x2 = seq( 0 , 1 , length.out = 100 ))

# z_pred stores the predictions
z_pred <- evaluate_smooths( z , newdata = pred_dat )

# build model
m <- model( z_pred )

# draw from the posterior
draws <- mcmc( m , n_samples = 200 )
# > running 4 chains simultaneously on up to 8 CPU cores
#>     warmup                                           0/1000 | eta:  ?s              warmup ==                                       50/1000 | eta: 30s              warmup ====                                    100/1000 | eta: 17s              warmup ======                                  150/1000 | eta: 12s              warmup ========                                200/1000 | eta: 10s              warmup ==========                              250/1000 | eta:  8s              warmup ===========                             300/1000 | eta:  7s              warmup =============                           350/1000 | eta:  6s              warmup ===============                         400/1000 | eta:  5s              warmup =================                       450/1000 | eta:  5s              warmup ===================                     500/1000 | eta:  4s              warmup =====================                   550/1000 | eta:  4s              warmup =======================                 600/1000 | eta:  3s              warmup =========================               650/1000 | eta:  3s              warmup ===========================             700/1000 | eta:  2s              warmup ============================            750/1000 | eta:  2s              warmup ==============================          800/1000 | eta:  1s              warmup ================================        850/1000 | eta:  1s              warmup ==================================      900/1000 | eta:  1s              warmup ====================================    950/1000 | eta:  0s              warmup ====================================== 1000/1000 | eta:  0s          
# >   sampling                                            0/200 | eta:  ?s            sampling ==========                                50/200 | eta:  1s            sampling ===================                      100/200 | eta:  0s            sampling ============================             150/200 | eta:  0s            sampling ======================================   200/200 | eta:  0s

# plot the mgcv fit
plot( b , scheme = 1 , shift = coef( b )[ 1 ])

# add in a line for each posterior sample
apply( draws [[ 1 ]], 1 , lines , x = pred_dat $ x2 , col = " blue " )
# > NULL

# plot the data
points( dat $ x2 , dat $ y , pch = 19 , cex = 0.2 )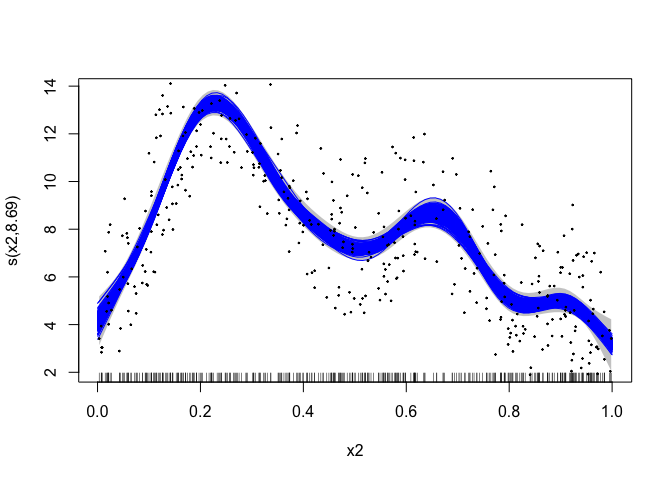

Kurze technische Details

greta.gam nutzt ein paar Tricks aus der jagam -Routine (Wood, 2016) in mgcv um die Dinge zum Laufen zu bringen. Hier einige kurze Details für diejenigen, die sich für die internen Abläufe interessieren …

Bayesianische Interpretation des GAM

GAMs sind Modelle mit bayesianischer Interpretation (auch wenn sie mit „frequentistischen“ Methoden angepasst werden). Man kann sich die glattere Strafmatrix als Prior-Präzisionsmatrix in einem Bayes'schen Zufallseffektmodell vorstellen. Designmatrizen werden genau wie im Fall des Frequentismus konstruiert. Weitere Hintergrundinformationen hierzu finden Sie in Miller (2021).

Strafmatrizen

Bei der bayesianischen Interpretation des GAM besteht eine leichte Schwierigkeit darin, dass die Prioren in ihrer naiven Form als Nullraum der Strafe ungeeignet sind (im 1D-Fall normalerweise der lineare Term). Um richtige Priors zu erhalten, können wir einen der „Tricks“ anwenden, die in Marra & Wood (2011) verwendet werden – nämlich die Teile der Strafe, die zum falschen Prior führen, irgendwie zu bestrafen. Wir nutzen die von jagam bereitgestellte Option und erstellen eine zusätzliche Strafmatrix für diese Terme (aus einer Eigenzerlegung der Strafmatrix; siehe Marra & Wood, 2011).