Python-Ausreißererkennung (PyOD)
Bereitstellung & Dokumentation & Statistiken & Lizenz

Lesen Sie mich zuerst
Willkommen bei PyOD, einer umfassenden, aber benutzerfreundlichen Python-Bibliothek zur Erkennung von Anomalien in multivariaten Daten. Unabhängig davon, ob Sie ein kleines Projekt oder große Datensätze in Angriff nehmen, bietet PyOD eine Reihe von Algorithmen, die Ihren Anforderungen gerecht werden.
- Für die Erkennung von Zeitreihenausreißern verwenden Sie bitte TODS.
- Für die Erkennung von Diagrammausreißern verwenden Sie bitte PyGOD.
- Leistungsvergleich und Datensätze : Wir verfügen über ein 45-seitiges, umfassendes Benchmark-Papier zur Anomalieerkennung. Das vollständig Open-Source-basierte ADBench vergleicht 30 Anomalieerkennungsalgorithmen anhand von 57 Benchmark-Datensätzen.
- Weitere Informationen zur Anomalieerkennung finden Sie unter Anomaly Detection Resources
- PyOD auf verteilten Systemen : Sie können PyOD auch auf Databricks ausführen.
Über PyOD
PyOD wurde 2017 gegründet und hat sich zu einer beliebten Python-Bibliothek zur Erkennung anomaler/abweichender Objekte in multivariaten Daten entwickelt. Dieses spannende und zugleich herausfordernde Gebiet wird allgemein als Ausreißererkennung oder Anomalieerkennung bezeichnet.
PyOD umfasst mehr als 50 Erkennungsalgorithmen, vom klassischen LOF (SIGMOD 2000) bis zum hochmodernen ECOD und DIF (TKDE 2022 und 2023). Seit 2017 wird PyOD in zahlreichen akademischen Forschungsprojekten und kommerziellen Produkten mit mehr als 22 Millionen Downloads erfolgreich eingesetzt. Es wird auch von der Community für maschinelles Lernen mit verschiedenen speziellen Beiträgen/Tutorials, darunter Analytics Vidhya, KDnuggets und Towards Data Science, sehr geschätzt.
PyOD wird vorgestellt für :
- Einheitliche, benutzerfreundliche Schnittstelle für verschiedene Algorithmen.
- Große Auswahl an Modellen , von klassischen Techniken bis hin zu den neuesten Deep-Learning-Methoden in PyTorch .
- Hohe Leistung und Effizienz , Nutzung von Numba und Joblib für die JIT-Kompilierung und Parallelverarbeitung.
- Schnelles Training und Vorhersage , erreicht durch das SUOD-Framework [50].
Ausreißererkennung mit 5 Codezeilen :
# Example: Training an ECOD detector
from pyod . models . ecod import ECOD
clf = ECOD ()
clf . fit ( X_train )
y_train_scores = clf . decision_scores_ # Outlier scores for training data
y_test_scores = clf . decision_function ( X_test ) # Outlier scores for test data
Auswahl des richtigen Algorithmus: Sie wissen nicht, wo Sie anfangen sollen? Betrachten Sie diese robusten und interpretierbaren Optionen:
- ECOD: Beispiel für die Verwendung von ECOD zur Ausreißererkennung
- Isolation Forest: Beispiel für die Verwendung von Isolation Forest zur Ausreißererkennung
Alternativ können Sie MetaOD für einen datengesteuerten Ansatz erkunden.
Unter Berufung auf PyOD :
Das PyOD-Papier wurde im Journal of Machine Learning Research (JMLR) veröffentlicht (MLOSS-Track). Wenn Sie PyOD in einer wissenschaftlichen Veröffentlichung verwenden, würden wir uns über Zitate zum folgenden Artikel freuen:
@article{zhao2019pyod,
Autor = {Zhao, Yue und Nasrullah, Zain und Li, Zheng},
title = {PyOD: Eine Python-Toolbox zur skalierbaren Ausreißererkennung},
Zeitschrift = {Journal of Machine Learning Research},
Jahr = {2019},
Volumen = {20},
Zahl = {96},
Seiten = {1-7},
URL = {http://jmlr.org/papers/v20/19-011.html}
}
oder:
Zhao, Y., Nasrullah, Z. und Li, Z., 2019. PyOD: Eine Python-Toolbox für die skalierbare Ausreißererkennung. Journal of Machine Learning Research (JMLR), 20(96), S. 1-7.
Eine umfassendere Perspektive zur Anomalieerkennung finden Sie in unseren NeurIPS-Artikeln ADBench: Anomaly Detection Benchmark Paper und ADGym: Design Choices for Deep Anomaly Detection:
@article{han2022adbench,
title={Adbench: Benchmark zur Anomalieerkennung},
Autor={Han, Songqiao und Hu, Xiyang und Huang, Hailiang und Jiang, Minqi und Zhao, Yue},
journal={Fortschritte in neuronalen Informationsverarbeitungssystemen},
Volumen={35},
Seiten={32142--32159},
Jahr={2022}
}
@article{jiang2023adgym,
title={ADGym: Design-Entscheidungen für die Erkennung tiefer Anomalien},
Autor={Jiang, Minqi und Hou, Chaochuan und Zheng, Ao und Han, Songqiao und Huang, Hailiang und Wen, Qingsong und Hu, Xiyang und Zhao, Yue},
journal={Fortschritte in neuronalen Informationsverarbeitungssystemen},
Volumen={36},
Jahr={2023}
}
Inhaltsverzeichnis :
- Installation
- API-Spickzettel und Referenz
- ADBench Benchmark und Datensätze
- Modell speichern und laden
- Schnellzug mit SUOD
- Schwellenwert für Ausreißerwerte
- Implementierte Algorithmen
- Schnellstart zur Ausreißererkennung
- So können Sie einen Beitrag leisten
- Einschlusskriterien
Installation
PyOD ist für eine einfache Installation mit pip oder conda konzipiert. Aufgrund häufiger Updates und Erweiterungen empfehlen wir die Verwendung der neuesten Version von PyOD:
pip install pyod # normal install
pip install --upgrade pyod # or update if needed
conda install -c conda-forge pyod
Alternativ können Sie die Datei setup.py klonen und ausführen:
git clone https://github.com/yzhao062/pyod.git
cd pyod
pip install .
Erforderliche Abhängigkeiten :
- Python 3.8 oder höher
- joblib
- matplotlib
- numpy>=1,19
- numba>=0,51
- scipy>=1.5.1
- scikit_learn>=0.22.0
Optionale Abhängigkeiten (siehe Details unten) :
- Combo (optional, erforderlich für models/combination.py und FeatureBagging)
- pytorch (optional, erforderlich für AutoEncoder und andere Deep-Learning-Modelle)
- suod (optional, erforderlich für die Ausführung des SUOD-Modells)
- xgboost (optional, erforderlich für XGBOD)
- pythresh (optional, für Schwellenwertbildung erforderlich)
API-Spickzettel und Referenz
Die vollständige API-Referenz ist in der PyOD-Dokumentation verfügbar. Unten finden Sie einen kurzen Spickzettel für alle Detektoren:
- fit(X) : Passen Sie den Detektor an. Der Parameter y wird in unüberwachten Methoden ignoriert.
- Entscheidungsfunktion(X) : Prognostizieren Sie mithilfe des angepassten Detektors rohe Anomaliewerte für X.
- Predict(X) : Bestimmen Sie mithilfe des angepassten Detektors anhand binärer Beschriftungen, ob eine Stichprobe ein Ausreißer ist oder nicht.
- predict_proba(X) : Schätzen Sie die Wahrscheinlichkeit, dass eine Stichprobe ein Ausreißer ist, mithilfe des angepassten Detektors.
- predict_confidence(X) : Bewerten Sie die Konfidenz des Modells pro Stichprobe (anwendbar in „predict“ und „predict_proba“) [35].
Hauptmerkmale eines angepassten Modells :
- Decision_scores_ : Ausreißerwerte der Trainingsdaten. Höhere Werte weisen typischerweise auf ein ungewöhnlicheres Verhalten hin. Ausreißer haben normalerweise höhere Werte.
- labels_ : Binäre Beschriftungen der Trainingsdaten, wobei 0 für Inliers und 1 für Ausreißer/Anomalien steht.
ADBench Benchmark und Datensätze
Wir haben gerade den 45-seitigen, umfassendsten ADBench: Anomaly Detection Benchmark [15] veröffentlicht. Das vollständig Open-Source-basierte ADBench vergleicht 30 Anomalieerkennungsalgorithmen anhand von 57 Benchmark-Datensätzen.
Die Organisation von ADBench ist unten aufgeführt:

Zur einfacheren Visualisierung führen wir den Vergleich ausgewählter Modelle über Compare_all_models.py durch.
Modell speichern und laden
PyOD verfolgt hinsichtlich der Modellpersistenz einen ähnlichen Ansatz wie sklearn. Zur Erläuterung siehe Modellpersistenz.
Kurz gesagt empfehlen wir die Verwendung von joblib oder pickle zum Speichern und Laden von PyOD-Modellen. Ein Beispiel finden Sie unter „examples/save_load_model_example.py“. Kurz gesagt, es ist einfach wie folgt:
from joblib import dump , load
# save the model
dump ( clf , 'clf.joblib' )
# load the model
clf = load ( 'clf.joblib' )
Es ist bekannt, dass die Speicherung neuronaler Netzwerkmodelle mit Herausforderungen verbunden ist. Überprüfen Sie Nr. 328 und Nr. 88 auf eine vorübergehende Problemumgehung.
Schnellzug mit SUOD
Schnelles Training und Vorhersage : Durch die Nutzung des SUOD-Frameworks ist es möglich, mit einer großen Anzahl von Erkennungsmodellen in PyOD zu trainieren und Vorhersagen zu treffen [50]. Siehe SUOD-Papier und SUOD-Beispiel.
from pyod . models . suod import SUOD
# initialized a group of outlier detectors for acceleration
detector_list = [ LOF ( n_neighbors = 15 ), LOF ( n_neighbors = 20 ),
LOF ( n_neighbors = 25 ), LOF ( n_neighbors = 35 ),
COPOD (), IForest ( n_estimators = 100 ),
IForest ( n_estimators = 200 )]
# decide the number of parallel process, and the combination method
# then clf can be used as any outlier detection model
clf = SUOD ( base_estimators = detector_list , n_jobs = 2 , combination = 'average' ,
verbose = False )
Schwellenwert für Ausreißerwerte
Bei der Festlegung des Verschmutzungsgrads kann ein stärker datenbasierter Ansatz gewählt werden. Mithilfe einer Schwellenwertmethode kann das Schätzen eines willkürlichen Werts durch bewährte Techniken zur Trennung von Inliers und Outliers ersetzt werden. Weitere Informationen zum Schwellenwert finden Sie unter PyThresh.
from pyod . models . knn import KNN
from pyod . models . thresholds import FILTER
# Set the outlier detection and thresholding methods
clf = KNN ( contamination = FILTER ())
Weitere Informationen zu den unterstützten Schwellenwertmethoden finden Sie unter „Schwellenwert“.
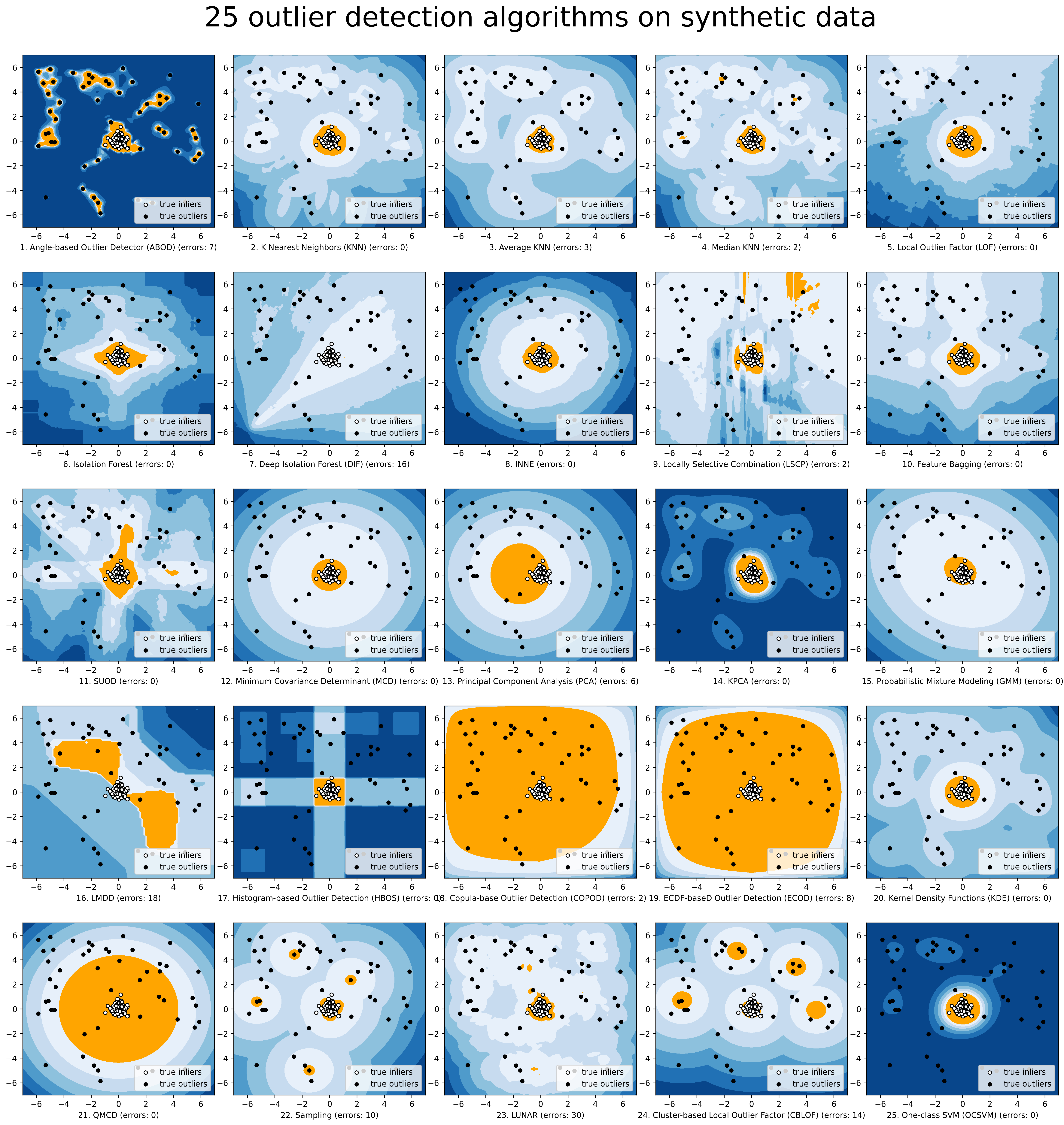
Implementierte Algorithmen
Das PyOD-Toolkit besteht aus vier Hauptfunktionsgruppen:
(i) Individuelle Erkennungsalgorithmen :
| Typ | Abk | Algorithmus | Jahr | Ref |
|---|
| Wahrscheinlichkeit | ECOD | Unüberwachte Ausreißererkennung mithilfe empirischer kumulativer Verteilungsfunktionen | 2022 | [28] |
| Wahrscheinlichkeit | ABOD | Winkelbasierte Ausreißererkennung | 2008 | [22] |
| Wahrscheinlichkeit | FastABOD | Schnelle winkelbasierte Ausreißererkennung mittels Näherung | 2008 | [22] |
| Wahrscheinlichkeit | COPOD | COPOD: Copula-basierte Ausreißererkennung | 2020 | [27] |
| Wahrscheinlichkeit | VERRÜCKT | Mittlere absolute Abweichung (MAD) | 1993 | [19] |
| Wahrscheinlichkeit | SOS | Stochastische Ausreißerauswahl | 2012 | [20] |
| Wahrscheinlichkeit | QMCD | Quasi-Monte-Carlo-Diskrepanz-Ausreißererkennung | 2001 | [11] |
| Wahrscheinlichkeit | KDE | Ausreißererkennung mit Kerndichtefunktionen | 2007 | [24] |
| Wahrscheinlichkeit | Probenahme | Schnelle distanzbasierte Ausreißererkennung durch Stichprobenziehung | 2013 | [42] |
| Wahrscheinlichkeit | GMM | Probabilistische Mischungsmodellierung für die Ausreißeranalyse | | [1] [Kap.2] |
| Lineares Modell | PCA | Hauptkomponentenanalyse (die Summe der gewichteten projizierten Abstände zu den Eigenvektor-Hyperebenen) | 2003 | [41] |
| Lineares Modell | KPCA | Kernel-Hauptkomponentenanalyse | 2007 | [18] |
| Lineares Modell | MCD | Minimale Kovarianzdeterminante (verwenden Sie die Mahalanobis-Abstände als Ausreißerwerte) | 1999 | [16] [37] |
| Lineares Modell | CD | Verwenden Sie die Cook-Distanz zur Erkennung von Ausreißern | 1977 | [10] |
| Lineares Modell | OCSVM | Ein-Klassen-Support-Vektor-Maschinen | 2001 | [40] |
| Lineares Modell | LMDD | Abweichungsbasierte Ausreißererkennung (LMDD) | 1996 | [6] |
| Näherungsbasiert | LOF | Lokaler Ausreißerfaktor | 2000 | [8] |
| Näherungsbasiert | COF | Konnektivitätsbasierter Ausreißerfaktor | 2002 | [43] |
| Näherungsbasiert | (Inkrementeller) COF | Speichereffizienter, konnektivitätsbasierter Ausreißerfaktor (langsamer, aber geringere Speicherkomplexität) | 2002 | [43] |
| Näherungsbasiert | CBLOF | Clustering-basierter lokaler Ausreißerfaktor | 2003 | [17] |
| Näherungsbasiert | LOCI | LOCI: Schnelle Ausreißererkennung mithilfe des lokalen Korrelationsintegrals | 2003 | [33] |
| Näherungsbasiert | HBOS | Histogrammbasierter Ausreißer-Score | 2012 | [12] |
| Näherungsbasiert | kNN | k Nächste Nachbarn (verwenden Sie die Entfernung zum k-ten nächsten Nachbarn als Ausreißerbewertung) | 2000 | [36] |
| Näherungsbasiert | Durchschn.KNN | Durchschnittlicher kNN (verwenden Sie den durchschnittlichen Abstand zu k nächsten Nachbarn als Ausreißerwert) | 2002 | [5] |
| Näherungsbasiert | MedKNN | Median kNN (verwenden Sie den Medianabstand zu k nächsten Nachbarn als Ausreißerwert) | 2002 | [5] |
| Näherungsbasiert | SOD | Erkennung von Subraum-Ausreißern | 2009 | [23] |
| Näherungsbasiert | STANGE | Rotationsbasierte Ausreißererkennung | 2020 | [4] |
| Ausreißer-Ensembles | IForest | Isolationswald | 2008 | [29] |
| Ausreißer-Ensembles | INNE | Isolationsbasierte Anomalieerkennung mithilfe von Nearest-Neighbor-Ensembles | 2018 | [7] |
| Ausreißer-Ensembles | DIF | Tiefer Isolationswald zur Anomalieerkennung | 2023 | [45] |
| Ausreißer-Ensembles | FB | Feature-Verpackung | 2005 | [25] |
| Ausreißer-Ensembles | LSCP | LSCP: Lokal selektive Kombination paralleler Ausreißer-Ensembles | 2019 | [49] |
| Ausreißer-Ensembles | XGBOD | Extreme Boosting-basierte Ausreißererkennung (überwacht) | 2018 | [48] |
| Ausreißer-Ensembles | LODA | Leichter Online-Detektor für Anomalien | 2016 | [34] |
| Ausreißer-Ensembles | SUOD | SUOD: Beschleunigung der unbeaufsichtigten Erkennung heterogener Ausreißer in großem Maßstab (Beschleunigung) | 2021 | [50] |
| Neuronale Netze | AutoEncoder | Vollständig verbundener AutoEncoder (Rekonstruktionsfehler als Ausreißerbewertung verwenden) | | [1] [Kap.3] |
| Neuronale Netze | VAE | Variationaler AutoEncoder (Rekonstruktionsfehler als Ausreißerbewertung verwenden) | 2013 | [21] |
| Neuronale Netze | Beta-VAE | Variationaler AutoEncoder (alle kundenspezifischen Verlustterme durch Variation von Gamma und Kapazität) | 2018 | [9] |
| Neuronale Netze | SO_GAAL | Einzieliges generatives kontradiktorisches aktives Lernen | 2019 | [30] |
| Neuronale Netze | MO_GAAL | Generatives kontradiktorisches aktives Lernen mit mehreren Zielen | 2019 | [30] |
| Neuronale Netze | DeepSVDD | Tiefe Ein-Klassen-Klassifizierung | 2018 | [38] |
| Neuronale Netze | AnoGAN | Anomalieerkennung mit generativen gegnerischen Netzwerken | 2017 | [39] |
| Neuronale Netze | ALAD | Gegnerisch erlernte Anomalieerkennung | 2018 | [47] |
| Neuronale Netze | AE1SVM | Autoencoder-basierte Ein-Klassen-Support-Vektor-Maschine | 2019 | [31] |
| Neuronale Netze | DevNet | Tiefenerkennung von Anomalien mit Abweichungsnetzwerken | 2019 | [32] |
| Graphenbasiert | R-Diagramm | Ausreißererkennung durch R-Graph | 2017 | [46] |
| Graphenbasiert | MOND | LUNAR: Vereinheitlichung lokaler Ausreißererkennungsmethoden über graphische neuronale Netze | 2022 | [13] |
(ii) Ausreißer-Ensembles und Ausreißer-Detektor-Kombinationsrahmen :
| Typ | Abk | Algorithmus | Jahr | Ref |
|---|
| Ausreißer-Ensembles | FB | Feature-Verpackung | 2005 | [25] |
| Ausreißer-Ensembles | LSCP | LSCP: Lokal selektive Kombination paralleler Ausreißer-Ensembles | 2019 | [49] |
| Ausreißer-Ensembles | XGBOD | Extreme Boosting-basierte Ausreißererkennung (überwacht) | 2018 | [48] |
| Ausreißer-Ensembles | LODA | Leichter Online-Detektor für Anomalien | 2016 | [34] |
| Ausreißer-Ensembles | SUOD | SUOD: Beschleunigung der unbeaufsichtigten Erkennung heterogener Ausreißer in großem Maßstab (Beschleunigung) | 2021 | [50] |
| Ausreißer-Ensembles | INNE | Isolationsbasierte Anomalieerkennung mithilfe von Nearest-Neighbor-Ensembles | 2018 | [7] |
| Kombination | Durchschnitt | Einfache Kombination durch Mittelung der Ergebnisse | 2015 | [2] |
| Kombination | Gewichteter Durchschnitt | Einfache Kombination durch Mittelung der Scores mit Detektorgewichten | 2015 | [2] |
| Kombination | Maximierung | Einfache Kombination durch Erzielung der Höchstpunktzahl | 2015 | [2] |
| Kombination | AOM | Durchschnitt vom Maximum | 2015 | [2] |
| Kombination | MOA | Maximierung des Durchschnitts | 2015 | [2] |
| Kombination | Mittlere | Einfache Kombination durch Bildung des Medians der Ergebnisse | 2015 | [2] |
| Kombination | Mehrheitsabstimmung | Einfache Kombination durch Mehrheitsentscheidung der Etiketten (Gewichte können verwendet werden) | 2015 | [2] |
(iii) Hilfsfunktionen :
| Typ | Name | Funktion | Dokumentation |
|---|
| Daten | generieren_daten | Generierung synthetisierter Daten; Normale Daten werden durch eine multivariate Gaußsche Funktion generiert und Ausreißer werden durch eine gleichmäßige Verteilung generiert | generieren_daten |
| Daten | generieren_daten_cluster | Generierung synthetisierter Daten in Clustern; Mit mehreren Clustern können komplexere Datenmuster erstellt werden | generieren_daten_cluster |
| Stat | wpearsonr | Berechnen Sie die gewichtete Pearson-Korrelation zweier Stichproben | wpearsonr |
| Dienstprogramm | get_label_n | Wandeln Sie rohe Ausreißerwerte in binäre Beschriftungen um, indem Sie den ersten n Ausreißerwerten 1 zuweisen | get_label_n |
| Dienstprogramm | precision_n_scores | Berechnen Sie die Genauigkeit @ Rang n | precision_n_scores |
Schnellstart zur Ausreißererkennung
PyOD wurde von der Community für maschinelles Lernen mit einigen vorgestellten Beiträgen und Tutorials gut gewürdigt.
Analytics Vidhya : Ein fantastisches Tutorial zum Erlernen der Ausreißererkennung in Python mithilfe der PyOD-Bibliothek
KDnuggets : Intuitive Visualisierung von Ausreißererkennungsmethoden, ein Überblick über Ausreißererkennungsmethoden von PyOD
Auf dem Weg zur Datenwissenschaft : Anomalieerkennung für Dummies
„examples/knn_example.py“ demonstriert die grundlegende API für die Verwendung des kNN-Detektors. Es wird darauf hingewiesen, dass die API bei allen anderen Algorithmen konsistent/ähnlich ist .
Ausführlichere Anweisungen zum Ausführen von Beispielen finden Sie im Beispielverzeichnis.
Initialisieren Sie einen kNN-Detektor, passen Sie das Modell an und treffen Sie die Vorhersage.
from pyod . models . knn import KNN # kNN detector
# train kNN detector
clf_name = 'KNN'
clf = KNN ()
clf . fit ( X_train )
# get the prediction label and outlier scores of the training data
y_train_pred = clf . labels_ # binary labels (0: inliers, 1: outliers)
y_train_scores = clf . decision_scores_ # raw outlier scores
# get the prediction on the test data
y_test_pred = clf . predict ( X_test ) # outlier labels (0 or 1)
y_test_scores = clf . decision_function ( X_test ) # outlier scores
# it is possible to get the prediction confidence as well
y_test_pred , y_test_pred_confidence = clf . predict ( X_test , return_confidence = True ) # outlier labels (0 or 1) and confidence in the range of [0,1]
Bewerten Sie die Vorhersage nach ROC und Precision @ Rank n (p@n).
from pyod . utils . data import evaluate_print
# evaluate and print the results
print ( " n On Training Data:" )
evaluate_print ( clf_name , y_train , y_train_scores )
print ( " n On Test Data:" )
evaluate_print ( clf_name , y_test , y_test_scores )
Sehen Sie sich eine Beispielausgabe und -visualisierung an.
On Training Data :
KNN ROC : 1.0 , precision @ rank n : 1.0
On Test Data :
KNN ROC : 0.9989 , precision @ rank n : 0.9
visualize ( clf_name , X_train , y_train , X_test , y_test , y_train_pred ,
y_test_pred , show_figure = True , save_figure = False )
Visualisierung (knn_figure):
Referenz
| [1] | (1, 2) Aggarwal, CC, 2015. Ausreißeranalyse. Im Data Mining (S. 237-263). Springer, Cham. |
| [2] | (1, 2, 3, 4, 5, 6, 7) Aggarwal, CC und Sathe, S., 2015. Theoretische Grundlagen und Algorithmen für Ausreißer-Ensembles. ACM SIGKDD Explorations Newsletter , 17(1), S. 24-47. |
| [3] | Aggarwal, CC und Sathe, S., 2017. Ausreißer-Ensembles: Eine Einführung. Springer. |
| [4] | Almardeny, Y., Boujnah, N. und Cleary, F., 2020. Eine neuartige Methode zur Erkennung von Ausreißern für multivariate Daten. IEEE-Transaktionen zu Wissen und Datentechnik . |
| [5] | (1, 2) Angiulli, F. und Pizzuti, C., 2002, August. Schnelle Ausreißererkennung in hochdimensionalen Räumen. In der Europäischen Konferenz über Prinzipien des Data Mining und der Wissensentdeckung, S. 15–27. |
| [6] | Arning, A., Agrawal, R. und Raghavan, P., 1996, August. Eine lineare Methode zur Abweichungserkennung in großen Datenbanken. In KDD (Bd. 1141, Nr. 50, S. 972–981). |
| [7] | (1, 2) Bandaragoda, TR, Ting, KM, Albrecht, D., Liu, FT, Zhu, Y. und Wells, JR, 2018, Isolationsbasierte Anomalieerkennung mithilfe von Ensembles nächster Nachbarn. Computational Intelligence , 34(4), S. 968-998. |
| [8] | Breunig, MM, Kriegel, HP, Ng, RT und Sander, J., 2000, Mai. LOF: Identifizierung dichtebasierter lokaler Ausreißer. ACM Sigmod Record , 29(2), S. 93-104. |
| [9] | Burgess, Christopher P., et al. „Entwirrung bei Beta-VAE verstehen.“ arXiv-Vorabdruck arXiv:1804.03599 (2018). |
| [10] | Cook, RD, 1977. Erkennung einflussreicher Beobachtungen in der linearen Regression. Technometrics, 19(1), S. 15-18. |
| [11] | Fang, KT und Ma, CX, 2001. Umfassende L2-Diskrepanz von Zufallsstichproben, lateinischen Hyperwürfeln und einheitlichen Designs. Zeitschrift für Komplexität, 17(4), S. 608-624. |
| [12] | Goldstein, M. und Dengel, A., 2012. Histogrammbasierter Ausreißer-Score (hbos): Ein schneller, unbeaufsichtigter Anomalieerkennungsalgorithmus. In KI-2012: Poster and Demo Track , S. 59-63. |
| [13] | Goodge, A., Hooi, B., Ng, SK und Ng, WS, 2022, Juni. Lunar: Vereinheitlichung lokaler Ausreißererkennungsmethoden über graphische neuronale Netze. In Proceedings of the AAAI Conference on Artificial Intelligence. |
| [14] | Gopalan, P., Sharan, V. und Wieder, U., 2019. PIDForest: Anomalieerkennung durch teilweise Identifizierung. In Advances in Neural Information Processing Systems, S. 15783-15793. |
| [15] | Han, S., Hu, X., Huang, H., Jiang, M. und Zhao, Y., 2022. ADBench: Anomaly Detection Benchmark. arXiv-Vorabdruck arXiv:2206.09426. |
| [16] | Hardin, J. und Rocke, DM, 2004. Ausreißererkennung in der Mehrfachclustereinstellung unter Verwendung des Determinantenschätzers für die minimale Kovarianz. Computational Statistics & Data Analysis , 44(4), S. 625-638. |
| [17] | He, Z., Xu, X. und Deng, S., 2003. Entdeckung Cluster-basierter lokaler Ausreißer. Pattern Recognition Letters , 24(9-10), S. 1641-1650. |
| [18] | Hoffmann, H., 2007. Kernel-PCA zur Neuheitserkennung. Mustererkennung, 40(3), S. 863-874. |
| [19] | Iglewicz, B. und Hoaglin, DC, 1993. Wie man Ausreißer erkennt und behandelt (Band 16). Asq Press. |
| [20] | Janssens, JHM, Huszár, F., Postma, EO und van den Herik, HJ, 2012. Stochastische Ausreißerauswahl. Technischer Bericht TiCC TR 2012-001, Universität Tilburg, Tilburg Centre for Cognition and Communication, Tilburg, Niederlande. |
| [21] | Kingma, DP und Welling, M., 2013. Auto-Encoding Variational Bayes. arXiv-Vorabdruck arXiv:1312.6114. |
| [22] | (1, 2) Kriegel, HP und Zimek, A., 2008, August. Winkelbasierte Ausreißererkennung in hochdimensionalen Daten. In KDD '08 , S. 444–452. ACM. |
| [23] | Kriegel, HP, Kröger, P., Schubert, E. und Zimek, A., 2009, April. Ausreißererkennung in achsenparallelen Unterräumen hochdimensionaler Daten. In Pacific-Asia Conference on Knowledge Discovery and Data Mining , S. 831–838. Springer, Berlin, Heidelberg. |
| [24] | Latecki, LJ, Lazarevic, A. und Pokrajac, D., 2007, Juli. Ausreißererkennung mit Kerndichtefunktionen. Im Internationalen Workshop zu maschinellem Lernen und Data Mining in der Mustererkennung (S. 61-75). Springer, Berlin, Heidelberg. |
| [25] | (1, 2) Lazarevic, A. und Kumar, V., 2005, August. Feature-Bagging zur Ausreißererkennung. Im KDD '05 . 2005. |
| [26] | Li, D., Chen, D., Jin, B., Shi, L., Goh, J. und Ng, SK, 2019, September. MAD-GAN: Multivariate Anomalieerkennung für Zeitreihendaten mit generativen gegnerischen Netzwerken. In International Conference on Artificial Neural Networks (S. 703-716). Springer, Cham. |
| [27] | Li, Z., Zhao, Y., Botta, N., Ionescu, C. und Hu, X. COPOD: Copula-basierte Ausreißererkennung. IEEE International Conference on Data Mining (ICDM) , 2020. |
| [28] | Li, Z., Zhao, Y., Hu, X., Botta, N., Ionescu, C. und Chen, HG ECOD: Unüberwachte Ausreißererkennung mithilfe empirischer kumulativer Verteilungsfunktionen. IEEE Transactions on Knowledge and Data Engineering (TKDE) , 2022. |
| [29] | Liu, FT, Ting, KM und Zhou, ZH, 2008, Dezember. Isolationswald. In International Conference on Data Mining , S. 413-422. IEEE. |
| [30] | (1, 2) Liu, Y., Li, Z., Zhou, C., Jiang, Y., Sun, J., Wang, M. und He, X., 2019. Generatives kontradiktorisches aktives Lernen zur unbeaufsichtigten Ausreißererkennung . IEEE-Transaktionen zu Wissen und Datentechnik . |
| [31] | Nguyen, MN und Vien, NA, 2019. Skalierbare und interpretierbare Ein-Klassen-SVMs mit Deep Learning und zufälligen Fourier-Funktionen. In Machine Learning and Knowledge Discovery in Databases: European Conference , ECML PKDD, 2018. |
| [32] | Pang, Guansong, Chunhua Shen und Anton Van Den Hengel. „Tiefe Anomalieerkennung mit Abweichungsnetzwerken.“ In KDD , S. 353–362. 2019. |
| [33] | Papadimitriou, S., Kitagawa, H., Gibbons, PB und Faloutsos, C., 2003, März. LOCI: Schnelle Ausreißererkennung mithilfe des lokalen Korrelationsintegrals. In ICDE '03 , S. 315-326. IEEE. |
| [34] | (1, 2) Pevný, T., 2016. Loda: Leichter Online-Detektor für Anomalien. Maschinelles Lernen , 102(2), S. 275–304. |
| [35] | Perini, L., Vercruyssen, V., Davis, J. Quantifizierung des Vertrauens von Anomaliedetektoren in ihre beispielweisen Vorhersagen. In Joint European Conference on Machine Learning and Knowledge Discovery in Databases (ECML-PKDD) , 2020. |
| [36] | Ramaswamy, S., Rastogi, R. und Shim, K., 2000, Mai. Effiziente Algorithmen zum Mining von Ausreißern aus großen Datensätzen. ACM Sigmod Record , 29(2), S. 427-438. |
| [37] | Rousseeuw, PJ und Driessen, KV, 1999. Ein schneller Algorithmus für den Determinantenschätzer der minimalen Kovarianz. Technometrics , 41(3), S. 212-223. |
| [38] | Ruff, L., Vandermeulen, R., Goernitz, N., Deecke, L., Siddiqui, SA, Binder, A., Müller, E. und Kloft, M., 2018, Juli. Tiefe Ein-Klassen-Klassifizierung. In der Internationalen Konferenz zum maschinellen Lernen (S. 4393-4402). PMLR. |
| [39] | Schlegl, T., Seeböck, P., Waldstein, SM, Schmidt-Erfurth, U. und Langs, G., 2017, Juni. Unüberwachte Anomalieerkennung mit generativen gegnerischen Netzwerken zur Steuerung der Markererkennung. In der Internationalen Konferenz zur Informationsverarbeitung in der medizinischen Bildgebung (S. 146-157). Springer, Cham. |
| [40] | Scholkopf, B., Platt, JC, Shawe-Taylor, J., Smola, AJ und Williamson, RC, 2001. Schätzung der Unterstützung einer hochdimensionalen Verteilung. Neural Computation , 13(7), S. 1443-1471. |
| [41] | Shyu, ML, Chen, SC, Sarinnapakorn, K. und Chang, L., 2003. Ein neuartiges Anomalieerkennungsschema basierend auf dem Hauptkomponentenklassifikator. MIAMI UNIV CORAL GABLES FL ABTEILUNG FÜR ELEKTRO- UND COMPUTERTECHNIK . |
| [42] | Sugiyama, M. und Borgwardt, K., 2013. Schnelle distanzbasierte Ausreißererkennung durch Stichprobenziehung. Fortschritte in neuronalen Informationsverarbeitungssystemen, 26. |
| [43] | (1, 2) Tang, J., Chen, Z., Fu, AWC und Cheung, DW, 2002, Mai. Verbesserung der Wirksamkeit der Ausreißererkennung für Muster mit geringer Dichte. In Pacific-Asia Conference on Knowledge Discovery and Data Mining , S. 535-548. Springer, Berlin, Heidelberg. |
| [44] | Wang, Wissensbasierte Systeme . |
| [45] | Xu, H., Pang, G., Wang, Y., Wang, Y., 2023. Tiefer Isolationswald zur Anomalieerkennung. IEEE-Transaktionen zu Wissen und Datentechnik . |
| [46] | You, C., Robinson, DP und Vidal, R., 2017. Nachweisbare, auf Selbstdarstellung basierende Ausreißererkennung in einer Union von Unterräumen. In Proceedings der IEEE-Konferenz über Computer Vision und Mustererkennung. |
| [47] | Zenati, H., Romain, M., Foo, CS, Lecouat, B. und Chandrasekhar, V., 2018, November. Gegnerisch erlernte Anomalieerkennung. Im Jahr 2018 IEEE International Conference on Data Mining (ICDM) (S. 727–736). IEEE. |
| [48] | (1, 2) Zhao, Y. und Hryniewicki, MK XGBOD: Verbesserung der überwachten Ausreißererkennung durch unüberwachtes Repräsentationslernen. IEEE International Joint Conference on Neural Networks , 2018. |
| [49] | (1, 2) Zhao, Y., Nasrullah, Z., Hryniewicki, MK und Li, Z., 2019, Mai. LSCP: Lokal selektive Kombination in parallelen Ausreißer-Ensembles. In Proceedings of the 2019 SIAM International Conference on Data Mining (SDM) , S. 585–593. Gesellschaft für Industrielle und Angewandte Mathematik. |
| [50] | (1, 2, 3, 4) Zhao, Y., Hu, X., Cheng, C., Wang, C., Wan, C., Wang, W., Yang, J., Bai, H., Li , Z., Xiao, C., Wang, Y., Qiao, Z., Sun, J. und Akoglu, L. (2021). SUOD: Beschleunigung der unbeaufsichtigten Erkennung heterogener Ausreißer in großem Maßstab. Konferenz über maschinelles Lernen und Systeme (MLSys) . |


