DDPM

Willkommen zum Buch: Die Kunst und Wissenschaft der Diffusionsmodelle in der generativen KI

(Entwurf, in Bearbeitung, voraussichtliches Veröffentlichungsdatum: Ende 2025 )

Vorwort

Dieses Lehrbuch wurde fachmännisch für Doktoranden der Physik und Informatik verfasst und bietet eine semesterlange, gründliche Untersuchung von Denoising Diffusion Probabilistic Models (DDPMs) im umfangreichen Bereich der generativen KI. Im Gegensatz zu herkömmlichen Texten, die einem starren, definitionstheoremsicheren Format folgen, nimmt dieses Buch einen entspannteren und gesprächigeren Ton an und enthält ausführliche Kommentare, Motivation und Erklärungen, um das Verständnis und das Engagement zu verbessern.

Bis vor Kurzem waren Diffusionsmodelle eine Nische, die nur einer ausgewählten Gruppe von Wissenschaftlern und Ingenieuren bekannt war. Generative KI, ein Bereich, der stark auf diese Modelle angewiesen ist, erfordert ein umfassendes Verständnis von Mathematik, Physik, stochastischen Prozessen, Deep Learning und Informatik.

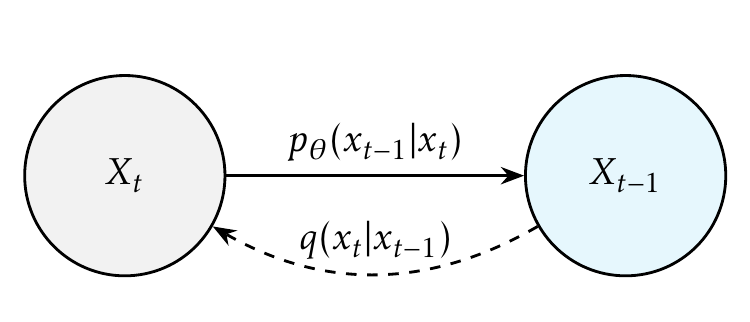
Dieses Buch befasst sich eingehend mit Diffusionsmodellen innerhalb der generativen KI und konzentriert sich insbesondere auf Denoising Diffusion Probabilistic Models (DDPMs) . Während andere generative Modelle wie Generative Adversarial Networks (GANs), Variational Autoencoders (VAEs) und flussbasierte Modelle die Generierung qualitativ hochwertiger Proben vorangebracht haben, weisen sie jeweils erhebliche Nachteile auf. GANs können instabiles Training und begrenzte Ausgabevielfalt erleben; VAEs hängen von komplexen Ersatzverlustfunktionen ab, was die Optimierung erschwert. und Strömungsmodelle erfordern spezielle, reversible Architekturen.

Diffusionsmodelle, die sich von der Nichtgleichgewichts-Thermodynamik inspirieren lassen, stellen eine robuste Alternative dar, indem sie diese Herausforderungen effektiv angehen. Dieser Band zeichnet sich dadurch aus, dass er sich ausschließlich auf Diffusionsmodelle konzentriert und eine einzigartige Perspektive bietet, die in anderen Texten selten zu finden ist. Dieser fokussierte Ansatz vereinfacht nicht nur komplexe Ideen für ein breiteres Publikum, sondern verschiebt auch die Grenzen dessen, was KI in modernen Industrien und Forschung erreichen kann. Daher ist dieses Buch eine unverzichtbare Ressource für jeden, der die aktuellen und zukünftigen Auswirkungen technologiegetriebener kreativer Prozesse in der generativen KI verstehen möchte.

Das Buch beginnt mit grundlegenden Konzepten wie der Einführung der Brownschen Bewegung – der einfachsten Form der Diffusion – und geht dann schrittweise zu komplexeren Diffusionsgleichungen über. Dieser strukturierte Ansatz stellt sicher, dass die Leser ein tiefgreifendes Verständnis sowohl der Vorwärts- als auch der Rückwärtsdiffusionsprozesse entwickeln und eine solide Grundlage für fortgeschrittene Studien und Anwendungen bieten.

Das Buch bietet eine detaillierte Untersuchung wichtiger Konzepte, darunter die Brownsche Bewegung, das Itô-Lemma, stochastische Differentialgleichungen (SDEs) und die bedeutende Rolle stochastischer Prozesse in der künstlichen Intelligenz. Es bietet eine umfassende Einführung in Diffusionsprozesse, eine sorgfältige Untersuchung von DDPMs und ein Kapitel, das den für DDPMs grundlegenden Deep-Learning-Architekturen gewidmet ist. Die Erzählung wird durch eine Fülle gelöster Probleme und zahlreiche Programmier-Miniprojekte bereichert, wobei der Schwerpunkt hauptsächlich auf Ergebnissen liegt, die für die praktische Umsetzung von erheblicher Relevanz sind. Als umfangreiches Lehr- und Nachschlagewerk für Hochschulabsolventen vertritt es die Philosophie, dass der effektivste Weg, etwas über DDPMs zu lernen, die Anwendung ist, die durch ausführliche Beispiele veranschaulicht wird, die die Theorie in realen Szenarien veranschaulichen.

Jedes Kapitel dieses Buches verbindet theoretischen Diskurs mit praktischen Anwendungen und gipfelt in Mini-Programmierprojekten mit Python . Diese Projekte ermöglichen es den Lesern, grundlegende theoretische Konzepte wie einen Random Walk oder die Brownsche Bewegung zu simulieren und zu anspruchsvolleren Implementierungen wie der Entwicklung eines DDPM überzugehen. Dieser praktische Ansatz festigt nicht nur das Lernen durch aktives Engagement, sondern vermittelt Studierenden und Fachleuten auch die Fähigkeiten, diese fortschrittlichen Modelle in verschiedenen realen Kontexten effektiv einzusetzen.

Darüber hinaus behandelt der Text methodisch Themen wie Stochastische Differentialgleichungen (SDEs), Brownsche Bewegung, Martingale und das Itô-Lemma. Diese Themen sind im Kontext von Diffusionsmodellen miteinander verknüpft und ermutigen die Leser, frühere Diskussionen erneut aufzugreifen, um die komplexen Zusammenhänge zwischen diesen Konzepten vollständig zu verstehen. Um Klarheit und Zugänglichkeit zu gewährleisten, verzichtet der Text bewusst auf einige eher esoterische Themen und konzentriert sich stattdessen auf die Bereitstellung von grundlegendem Wissen und tiefen Einblicken, die für ein umfassendes Verständnis von DDPMs unerlässlich sind.

Bildungsziele

Dieses Manuskript ist reich an einer Vielzahl vollständig gelöster Beispiele und Übungen unterschiedlicher Komplexität und integriert diese in die Erzählung, um das Verständnis des Lesers umfassend zu verbessern und zu beurteilen. Diese Übungen sind von zentraler Bedeutung für die Struktur des Buches und werden in nachfolgenden Diskussionen häufig erwähnt, um eine dynamische und interaktive Lernumgebung zu fördern.

Inspiriert von der renommierten Schaum's Outline-Reihe verbindet der Text eine strenge theoretische Darstellung mit praktischen Anwendungen. Diese Methodik ist darauf ausgelegt, theoretisches Wissen durch praktische Problemlösung zu festigen und dadurch das Verständnis zu verbessern.

Methodischer Ansatz

Obwohl der Schwerpunkt hauptsächlich auf der Theorie liegt, enthält der Text gelegentlich Codeschnipsel, um die Lücke zwischen Theorie und praktischer Anwendung zu schließen, was ihn ideal für Doktoranden und Fachleute macht, die sich der Beherrschung von Diffusionsmodellen widmen.

Jeder Abschnitt jedes Kapitels ist so gegliedert, dass er Folgendes enthält:

1. Eine Einführung in die Konzepte,
2. Relevante Definitionen und Theoreme,
3. Probleme und detaillierte Lösungen.

Beispielproblem: Standard-Brownsche Bewegung und stochastische Integrale

Miniprojekte programmieren

Um den pädagogischen Wert jedes Kapitels zu steigern und die vorgestellten theoretischen Konzepte zu festigen, schließt der Text mit einer Reihe praktischer Programmierprojekte ab. Diese Projekte sollen die Lücke zwischen Theorie und Praxis schließen und es den Lesern ermöglichen, ihr neu erworbenes Wissen in simulierten Umgebungen anzuwenden. Dieser praktische Ansatz stärkt nicht nur das Verständnis, sondern schärft auch praktische Fähigkeiten, die für den Fortschritt im Bereich der generativen KI unerlässlich sind.

Zu den Projekten gehören:

• 1D-Simulation der Brownschen Bewegung: Beschäftigen Sie sich mit dem grundlegenden stochastischen Prozess, indem Sie Partikelbewegungen in einer Flüssigkeit simulieren und so die von Robert Brown beobachtete Zufallsbewegung nachahmen.
• Vorwärtsdiffusionssimulation: Entwickeln Sie ein Programm, um die fortschreitende Hinzufügung von Rauschen zu einem System zu modellieren und zu veranschaulichen, wie sich Daten im Laufe der Zeit in einen chaotischeren Zustand entwickeln.
• Rückwärtsdiffusionssimulation: Implementieren Sie die Umkehrung des Vorwärtsdiffusionsprozesses und demonstrieren Sie Techniken zur Wiederherstellung der Originaldaten aus ihrem verrauschten Zustand.
• Ornstein-Uhlenbeck (OU)-Prozesssimulation: Simulieren Sie diesen stochastischen Prozess mit Umkehrung des Mittelwerts, der üblicherweise zur Modellierung von Zinssätzen und anderen Finanzindikatoren verwendet wird.
• Entwicklung eines probabilistischen Kernmodells zur Rauschunterdrückung (DPM): Erstellen Sie eine Basisversion eines Entrauschungsmodells, um die grundlegenden Mechanismen und Algorithmen zu verstehen, die diese Systeme antreiben.
• Vollständige Realisierung eines Denoising Diffusion Probabilistic Model (DDPM): Erstellen Sie ein umfassendes DDPM, um seine Anwendung bei der Generierung hochwertiger synthetischer Daten zu untersuchen.
• Implementierung von Stichprobenalgorithmen: Erstellen und testen Sie verschiedene Stichprobenalgorithmen, die eine entscheidende Rolle bei der Generierung von Ausgaben aus trainierten Modellen spielen.

Diese Projekte fördern ein tiefes Eintauchen in die praktischen Aspekte stochastischer Prozesse und Diffusionsmodelle und bereiten die Leser darauf vor, reale Probleme anzugehen und Innovationen im Bereich der generativen KI zu entwickeln.