Startseite | Installation | Dokumentation | Anleitung | Entwickler
rodeo ist eine schnelle Python-Bibliothek, die probabilistische Numerik zur Lösung gewöhnlicher Differentialgleichungen (ODEs) verwendet. Das heißt, die meisten ODE-Löser (z. B. die Euler-Methode) erzeugen eine deterministische Näherung an die ODE auf einem Gitter mit Schrittweite
Rodeo bietet eine leichte und erweiterbare Familie von Approximationen für ein nichtlineares Bayes'sches Filterparadigma, das vielen probabilistischen Lösern gemeinsam ist (Tronarp et al. (2018)). Dies beginnt damit, dass der ODE-Lösung ein Gaußscher Prozess vorangestellt wird und dieser nacheinander aktualisiert wird, während der Löser das Gitter durchläuft. Rodeo basiert auf Jax , was eine Just-in-Time-Kompilierung und automatische Differenzierung ermöglicht. Die API von jax entspricht fast der von numpy .
Rodeo bietet zwei Hauptwerkzeuge: eines zur Approximation der ODE-Lösung und das andere zur Parameterinferenz. Für Ersteres bieten wir:
solve : Implementierung eines probabilistischen ODE-Lösers, der ein nichtlineares Bayes'sches Filterparadigma verwendet.Für Letzteres stellen wir die Likelihood-Approximationsmethoden zur Verfügung:
basic : Implementierung einer einfachen Likelihood-Approximationsmethode (Details finden Sie in Wu und Lysy (2023)).fenrir : Implementierung von Fenrir (Tronarp et al (2022)).marginal_mcmc : MCMC-Implementierung der Methode von Chkrebtii (Chkrebtii et al (2016)).dalton : Implementierung unserer datenadaptiven ODE-Likelihood-Approximation (Wu und Lysy (2023)).Detaillierte Beispiele für deren Verwendung finden Sie im Abschnitt Dokumentation. Bitte beachten Sie, dass dies die reine Jax -Version von Rodeo ist. Informationen zu den Legacy-Versionen mit verschiedenen anderen Backends finden Sie hier.
Laden Sie das Repo von GitHub herunter und installieren Sie es dann mit dem Skript setup.cfg :
git clone https://github.com/mlysy/rodeo.git
cd rodeo
pip install . Bitte gehen Sie zunächst zu readthedocs, um die gerenderte Dokumentation für die folgenden Beispiele anzuzeigen.
Ein Schnellstart-Tutorial zur Lösung eines einfachen ODE-Problems.
Ein Beispiel für die Lösung einer ODE höherer Ordnung.
Ein Beispiel für die Lösung einer schwierigen chaotischen ODE.
Ein Beispiel für ein Parameterinferenzproblem, bei dem wir die Laplace-Näherung verwenden.
In dieser exemplarischen Vorgehensweise zeigen wir, wie man eine ODE mit unserem probabilistischen Löser löst und Parameterinferenz durchführt. Wir werden zunächst den Aufbau zur Lösung der ODE veranschaulichen. Betrachten wir zu diesem Zweck das folgende ODE-Beispiel erster Ordnung ( FitzHugh-Nagumo -Modell):
wo die Lösung
Nach der Notation von (Wu und Lysy (2023)) haben wir
für
import jax
import jax . numpy as jnp
import rodeo
def fitz_fun ( X , t , ** params ):
"FitzHugh-Nagumo ODE in rodeo format."
a , b , c = params [ "theta" ]
V , R = X [:, 0 ]
return jnp . array (
[[ c * ( V - V * V * V / 3 + R )],
[ - 1 / c * ( V - a + b * R )]]
)
def fitz_init ( x0 , theta ):
"FitzHugh-Nagumo initial values in rodeo format."
x0 = x0 [:, None ]
return jnp . hstack ([
x0 ,
fitz_fun ( X = x0 , t = 0. , theta = theta ),
jnp . zeros_like ( x0 )
])
W = jnp . array ([[[ 0. , 1. , 0. ]], [[ 0. , 1. , 0. ]]]) # LHS matrix of ODE
x0 = jnp . array ([ - 1. , 1. ]) # initial value for the ODE-IVP
theta = jnp . array ([ .2 , .2 , 3 ]) # ODE parameters
X0 = fitz_init ( x0 , theta ) # initial value in rodeo format
# Time interval on which a solution is sought.
t_min = 0.
t_max = 40.
# --- Define the prior process -------------------------------------------
n_vars = 2 # number of variables in the ODE
n_deriv = 3 # max number of derivatives
sigma = jnp . array ([ .1 ] * n_vars ) # IBM process scale factor
# --- data simulation ------------------------------------------------------
n_steps = 800 # number of evaluations steps
dt = ( t_max - t_min ) / n_steps # step size
# generate the Kalman parameters corresponding to the prior
prior_Q , prior_R = rodeo . prior . ibm_init (
dt = dt_sim ,
n_deriv = n_deriv ,
sigma = sigma
)
# Produce a Pseudo-RNG key
key = jax . random . PRNGKey ( 0 )
Xt , _ = rodeo . solve_mv (
key = key ,
# define ode
ode_fun = fitz_fun ,
ode_weight = W ,
ode_init = X0 ,
t_min = t_min ,
t_max = t_max ,
theta = theta , # ODE parameters added here
# solver parameters
n_steps = n_steps ,
interrogate = rodeo . interrogate . interrogate_kramer ,
prior_weight = prior_Q ,
prior_var = prior_R
) Wir vergleichen die Lösung des Lösers mit der deterministischen Lösung, die von odeint in der Scipy -Bibliothek bereitgestellt wird.
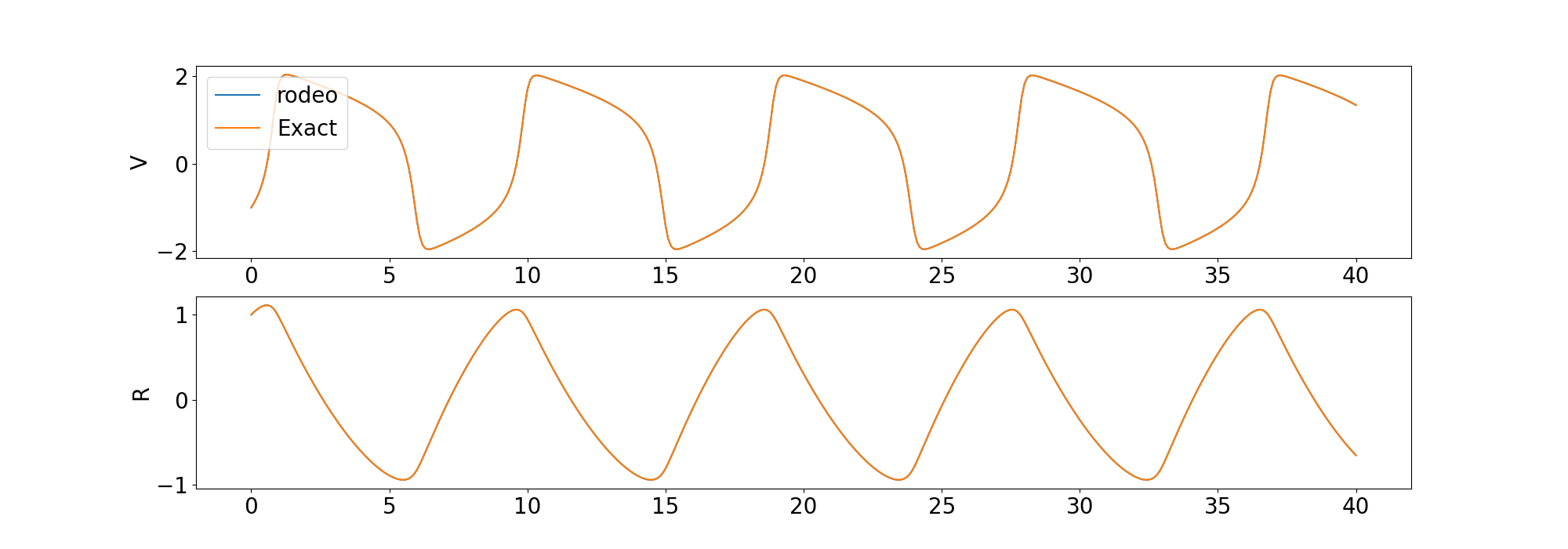
Wir enthalten auch Beispiele für die Lösung einer ODE höherer Ordnung und einer chaotischen ODE.
Wir wenden uns nun dem Problem der Parameterinferenz zu. Rodeo enthält mehrere Likelihood-Approximationsmethoden, die im Abschnitt Beschreibung zusammengefasst sind. Hier verwenden wir die basic Likelihood-Approximationsmethode. Angenommen, Beobachtungen werden über das Modell simuliert
Wo basic Likelihood-Näherung für zu erstellen
def fitz_logprior ( upars ):
"Logprior on unconstrained model parameters."
n_theta = 5 # number of ODE + IV parameters
lpi = jax . scipy . stats . norm . logpdf (
x = upars [: n_theta ],
loc = 0. ,
scale = 10.
)
return jnp . sum ( lpi )
def fitz_loglik ( obs_data , ode_data , ** params ):
"""
Loglikelihood for measurement model.
Args:
obs_data (ndarray(n_obs, n_vars)): Observations data.
ode_data (ndarray(n_obs, n_vars, n_deriv)): ODE solution.
"""
ll = jax . scipy . stats . norm . logpdf (
x = obs_data ,
loc = ode_data [:, :, 0 ],
scale = 0.005
)
return jnp . sum ( ll )
def constrain_pars ( upars , dt ):
"""
Convert unconstrained optimization parameters into rodeo inputs.
Args:
upars : Parameters vector on unconstrainted scale.
dt : Discretization grid size.
Returns:
tuple with elements:
- theta : ODE parameters.
- X0 : Initial values in rodeo format.
- Q, R : Prior matrices.
"""
theta = jnp . exp ( upars [: 3 ])
x0 = upars [ 3 : 5 ]
X0 = fitz_init ( x0 , theta )
sigma = upars [ 5 :]
Q , R = rodeo . prior . ibm_init (
dt = dt ,
n_deriv = n_deriv ,
sigma = sigma
)
return theta , X0 , Q , R
def neglogpost_basic ( upars ):
"Negative logposterior for basic approximation."
# solve ODE
theta , X0 , prior_Q , prior_R = constrain_pars ( upars , dt_sim )
# basic loglikelihood
ll = rodeo . inference . basic (
key = key ,
# ode specification
ode_fun = fitz_fun ,
ode_weight = W ,
ode_init = X0 ,
t_min = t_min ,
t_max = t_max ,
theta = theta ,
# solver parameters
n_steps = n_steps ,
interrogate = rodeo . interrogate . interrogate_kramer ,
prior_weight = prior_Q ,
prior_var = prior_R ,
# observations
obs_data = obs_data ,
obs_times = obs_times ,
obs_loglik = fitz_loglik
)
return - ( ll + fitz_logprior ( upars )) Dies ist ein einfaches Beispiel zur Demonstration der Verwendung. Wir schlagen ausgefeiltere Likelihood-Näherungen vor, die die Lösungsunsicherheit auf die Likelihood-Näherung übertragen, wie z. B. fenrir , marginal_mcmc und dalton . Weitere Informationen finden Sie im Tutorial zur Parameterinferenz.
Hier sind einige Ergebnisse, die durch verschiedene Wahrscheinlichkeitsnäherungen im Rodeo aus /examples/ erzielt wurden:
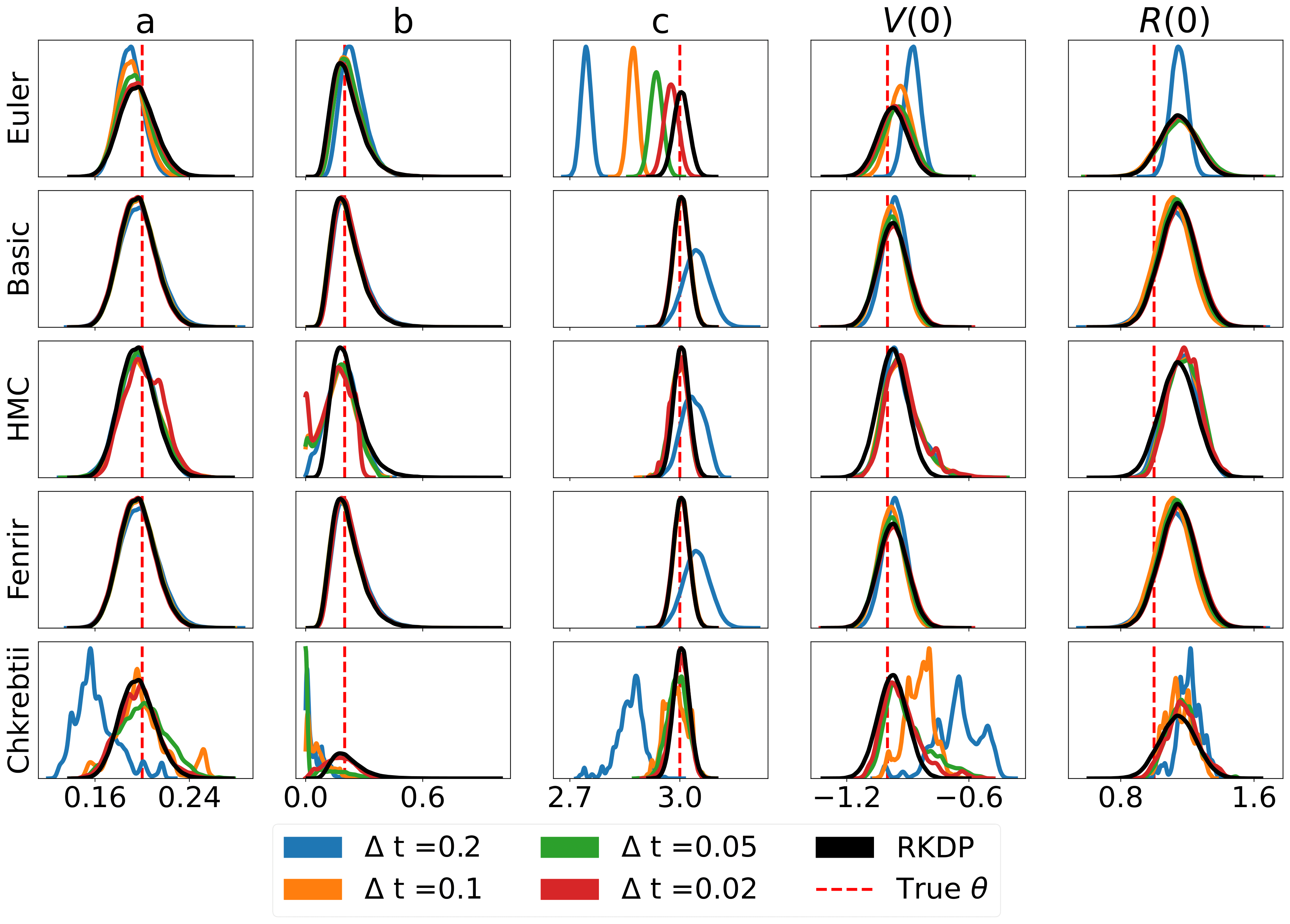
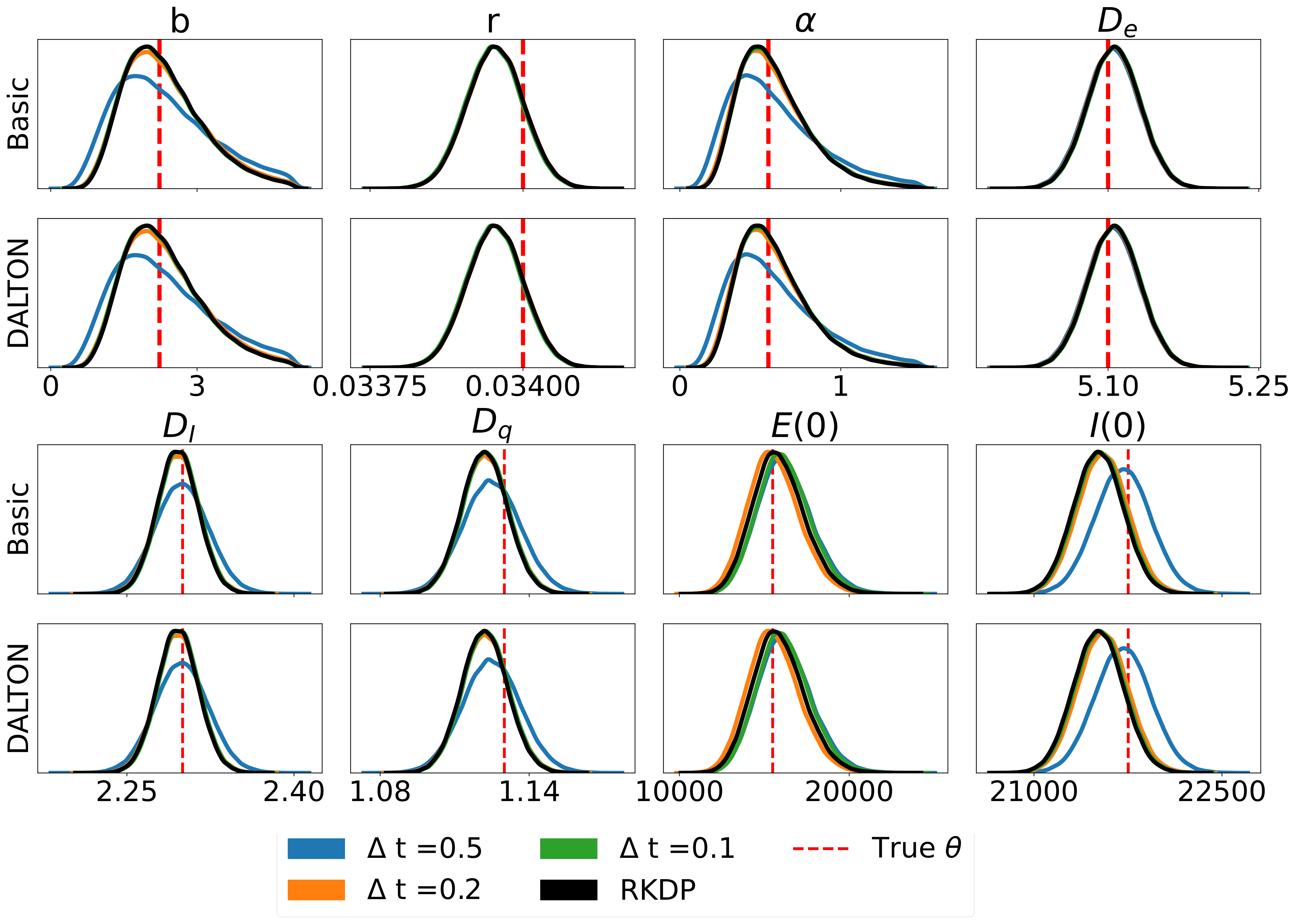
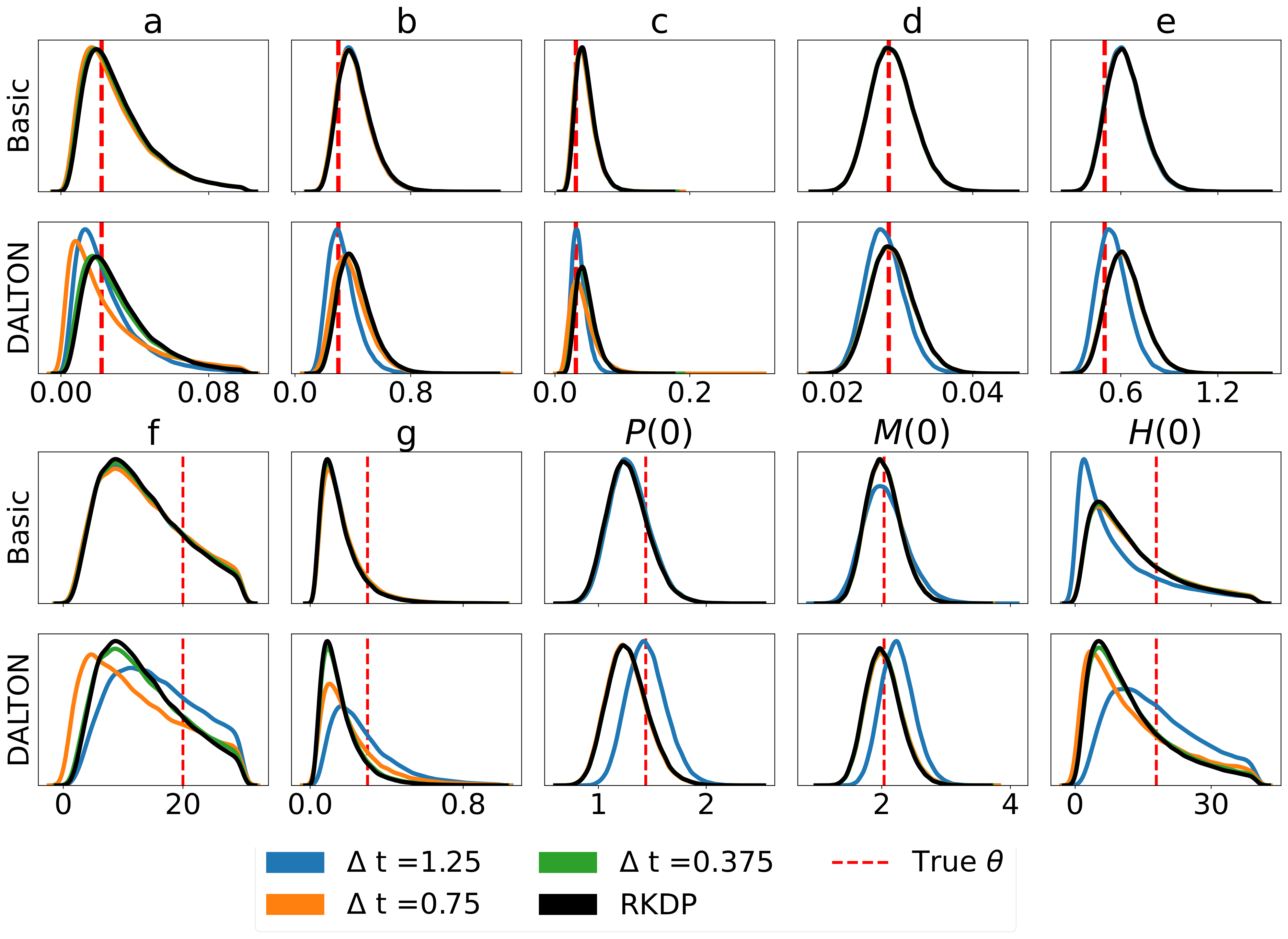
Die Unit-Tests können über die folgenden Befehle ausgeführt werden:
cd tests
python -m unittest discover -v Oder installieren Sie tox und geben Sie dann in rodeo die Befehlszeile ein: tox .
Die HTML-Dokumentation kann aus dem Stammordner kompiliert werden:
pip install .[docs]
cd docs
make html Dadurch wird die Dokumentation in docs/build erstellt.