awesome latex drawing

Tolle LaTeX-Zeichnung

Hergestellt von Xinyu Chen • https://xinychen.github.io

awesome-latex-drawing ist eine Sammlung von über 30 akademischen Zeichenbeispielen für die Verwendung von LaTeX, darunter Bayes'sche Netzwerke, Funktionsdiagramme, grafische Modelle, Tensorstruktur und technische Frameworks.

Beschreibung

LaTeX ist ein hochwertiges Schriftsatzsystem, das als kostenlose Software verfügbar ist und in den letzten Jahren häufig für die Erstellung akademischer Grafiken verwendet wurde. Seine Beliebtheit beruht auf seiner Fähigkeit, komplexe Illustrationen mit speziellen Symbolen und mathematischen Gleichungen zu verarbeiten, was es ideal zum Zeichnen detaillierter Grafiken in der Forschung macht.

Dieses Projekt stellt mehrere mit LaTeX erstellte Grafiken vor, mit Beispielen, die auf Overleaf, einer beliebten Online-LaTeX-Plattform, leicht nachzuvollziehen sind. Wenn Sie interessiert sind, können Sie unsere Beispiele gerne auf Overleaf unter overleaf.com erkunden und reproduzieren.

Inhalt

Beispieltabelle

• Bayesianische Netzwerke
  • Bayesianisches Netzwerk der Bayesianischen CP-Faktorisierung (BCPF)
  • Bayesianisches Netzwerk der Bayesian Gaußian CP (BGCP)-Faktorisierung
  • Bayesianisches Netzwerk der Bayesian Augmented Tensor Factorization (BATF)
  • Bayesianisches Netzwerk der Bayesianischen zeitlichen Matrixfaktorisierung (BTMF)
  
  
• Grafische Modelle
  • Teilweise beobachtete Zeitreihenmatrix und Tensor
  • Vorhersage von Matrix- und Tensor-Zeitreihen bei Vorhandensein fehlender Werte
  • Ungerichtete und zirkulierende Graphen auf den relationalen Datenproben mit bestimmten Graden
  • Laplace-Faltungs-Zeitreihenmodellierung
  
  
• Plotten der Funktion pgfplots
  • PDF- und CDF-Funktionen der Erlang-Verteilung
  • PDF der Normalverteilung mit unterschiedlichen Mittelwerten und Varianzen
  • (Gemeinsame) PDF-Funktionen von Lognormalverteilungen
  • Iterativer Prozess des konjugierten Gradienten zur Lösung eines linearen Gleichungssystems
  • Zufällige und nicht zufällige fehlende Muster
  • Sinus- und Cosinusfunktionen
  • Mechanismus der Zeitreihenvorhersage
  
  
• tikz für Matrixstruktur
  • Grafische Darstellung des Problems der multivariaten Zeitreihenvorhersage
  • Grafische Darstellung der zeitlichen Matrixfaktorisierung
  • Grafische Darstellung der rollierenden Zeitreihenvorhersage mit zeitlicher Matrixfaktorisierung
  
  
• tikz-3dplot für Tensorstruktur
  • Grafische Darstellung des Tensors (Ursprung, Ziel, Zeitfenster).
  • Grafische Darstellung der klassischen CP-Tensorfaktorisierung auf einem Tensor dritter Ordnung
  • Grafische Darstellung des Augmented Tensor Factorization (AuTF)-Modells
  • Grafische Darstellung der Tensor-Vervollständigungsaufgabe und ihres Rahmenwerks
  • Grafische Darstellung des niedrigrangigen autoregressiven Tensor-Vervollständigungsmodells
  • Grafische Darstellung des Singularwert-Schwellenwertbildungsprozesses der Tensordaten mit einheitlicher Transformation
  • Grafische Darstellung des Tensor-Vervollständigungsmodells mit niedrigem Rang
  • Grafische Darstellung des Low-Rank-Tensor-Regressionsmodells

Galerie

Suchen Sie nach guten LaTeX-Zeichnungsbeispielen? Hier finden Sie über 30 Grafiken, die zeigen, wie man in LaTaX zeichnet.

Bayesianische Netzwerke

LaTeX bietet einige leistungsstarke domänenspezifische Pakete und Tools wie tikz um flexible grafische Modelle zu ermöglichen. Bayesianische Netzwerke stellen eine Familie grafischer Modelle dar, die aus Variablen (normalerweise durch Knoten gekennzeichnet) und Abhängigkeitsbeziehungen (normalerweise durch Pfeile gekennzeichnet) bestehen. Glücklicherweise verfügt tikz über eine spezielle Bibliothek zum Zeichnen von Bayes'schen Netzwerken und gerichteten Faktorgraphen.

Eine weitere Toolbox in Python: https://docs.daft-pgm.org/en/latest/

Bayesianische Tensorfaktorisierung

[Beispiel 1]

Dieses Beispiel stammt aus dem folgenden Artikel:

• Qibin Zhao, Liqing Zhang, Andrzej Cichocki (2015). Bayesianische CP-Faktorisierung unvollständiger Tensoren mit automatischer Rangbestimmung. IEEE Transactions on Pattern Analysis and Machine Intelligence, 37(9): 1751-1763.

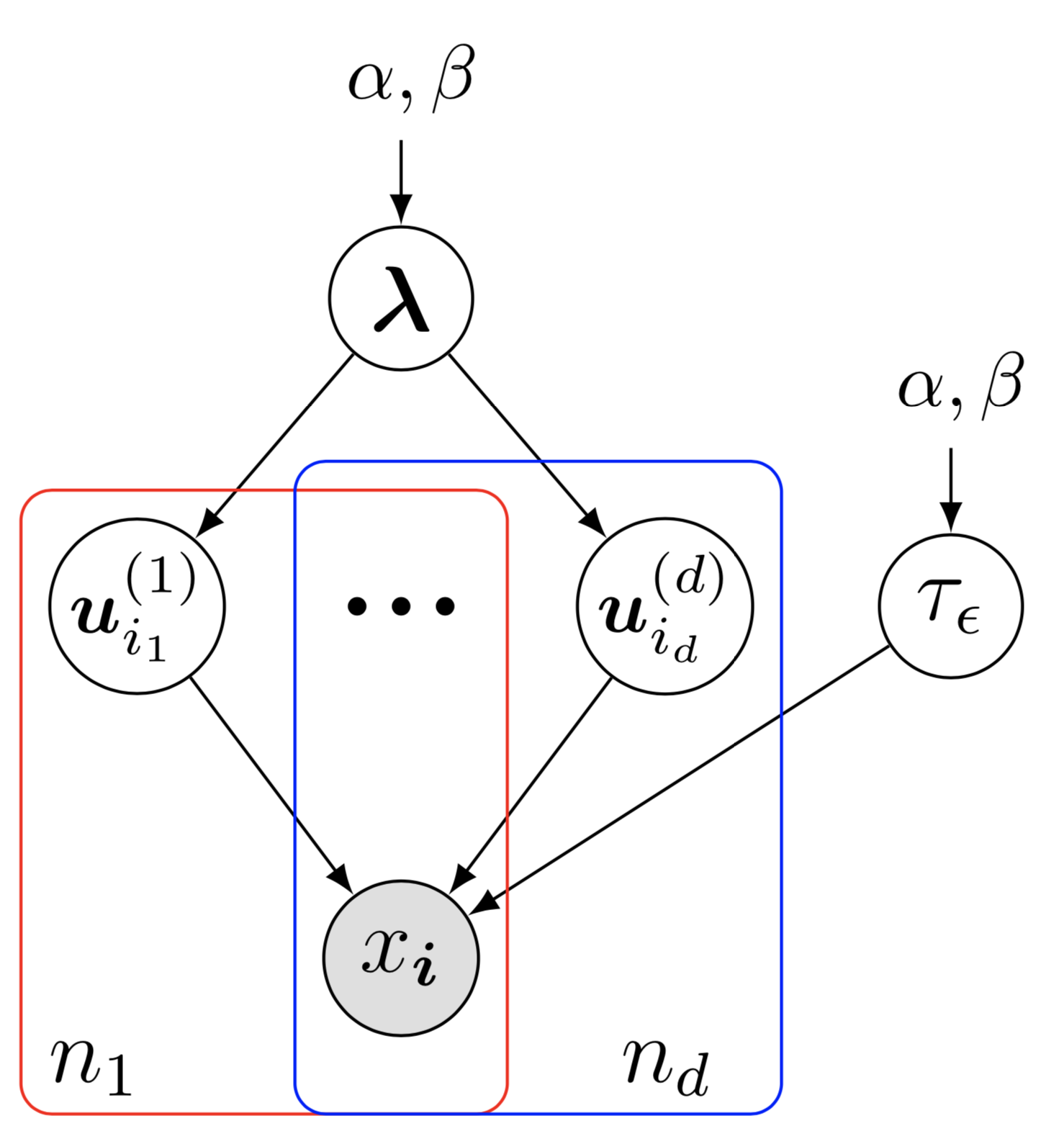Dies zeigt das Bayesian Network of Bayesian CP Factorization (BCPF)-Modell. Um dieses Beispiel für ein Bayes'sches Netzwerk zu zeichnen, müssen einige Vorbereitungen getroffen werden:

• preamble :
  1. Definieren Sie die documentclass als standalone , z. B. documentclass[border = 0.1cm]{standalone} mit 0,1 cm Rand,
  2. Verwenden Sie das Paket tikz , also usepackage{tikz} , und verwenden Sie tikz -Bibliothek wie usetikzlibrary{bayesnet} die ein wichtiges Werkzeug zum Zeichnen von Bayes'schen Netzwerken und gerichteten Faktorgraphen ist.
  3. Legen Sie den tikz -Stil mit dem Befehl tikzstyle{} fest.
  4. Verwenden Sie Umgebungen für mathematische Gleichungen, einschließlich usepackage{amsfonts, amsmath, amssymb} .
• body :
  1. Verwenden Sie begin{tikzpicture} end{tikzpicture} um mit dem Zeichnen zu beginnen.
  2. Verwenden Sie node , um Knoten und Textfelder im Bayes'schen Netzwerk zu definieren.
  3. Verwenden Sie path , um Pfeile im Bayes'schen Netzwerk zu definieren.
  4. Verwenden Sie plate um Platten im Bayes'schen Netzwerk zu definieren.

Bitte klicken Sie auf das Bild und sehen Sie sich den Quellcode an.

• Öffnen Sie BGCP.tex in Ihrem umseitigen Projekt, dann sehen Sie die folgenden Bilder zum BGCP-Modell (Bayesian Gaußian CP decomposition) als Bayesianisches Netzwerk und einen gerichteten Faktorgraphen:

[Beispiel 2]

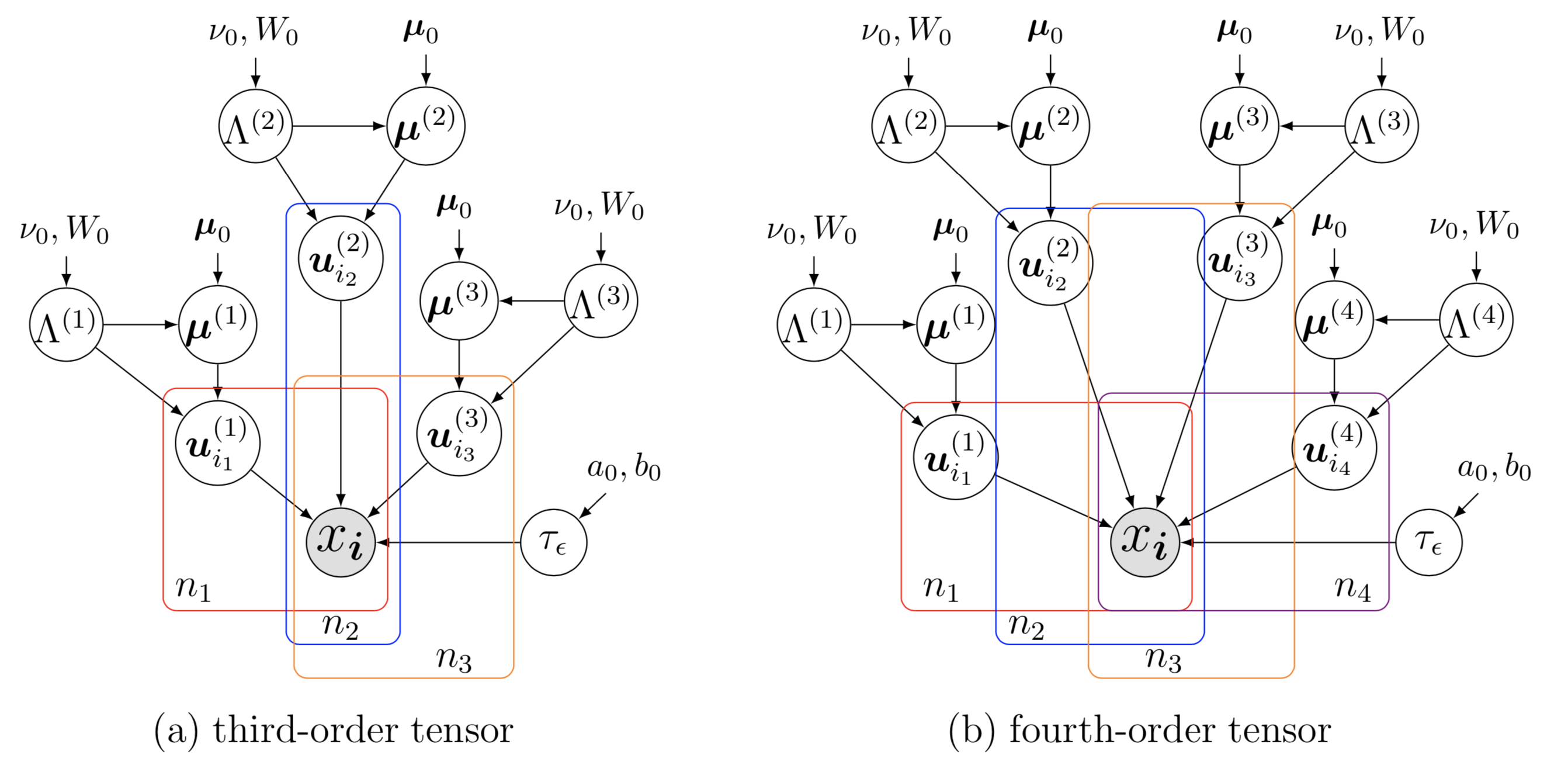
Dieses Beispiel stammt aus dem folgenden Artikel:

Xinyu Chen, Zhaocheng He, Lijun Sun (2019). Ein Bayes'scher Tensorzerlegungsansatz für die raumzeitliche Imputation von Verkehrsdaten. Transportforschung Teil C: Emerging Technologies, 98: 73-84.

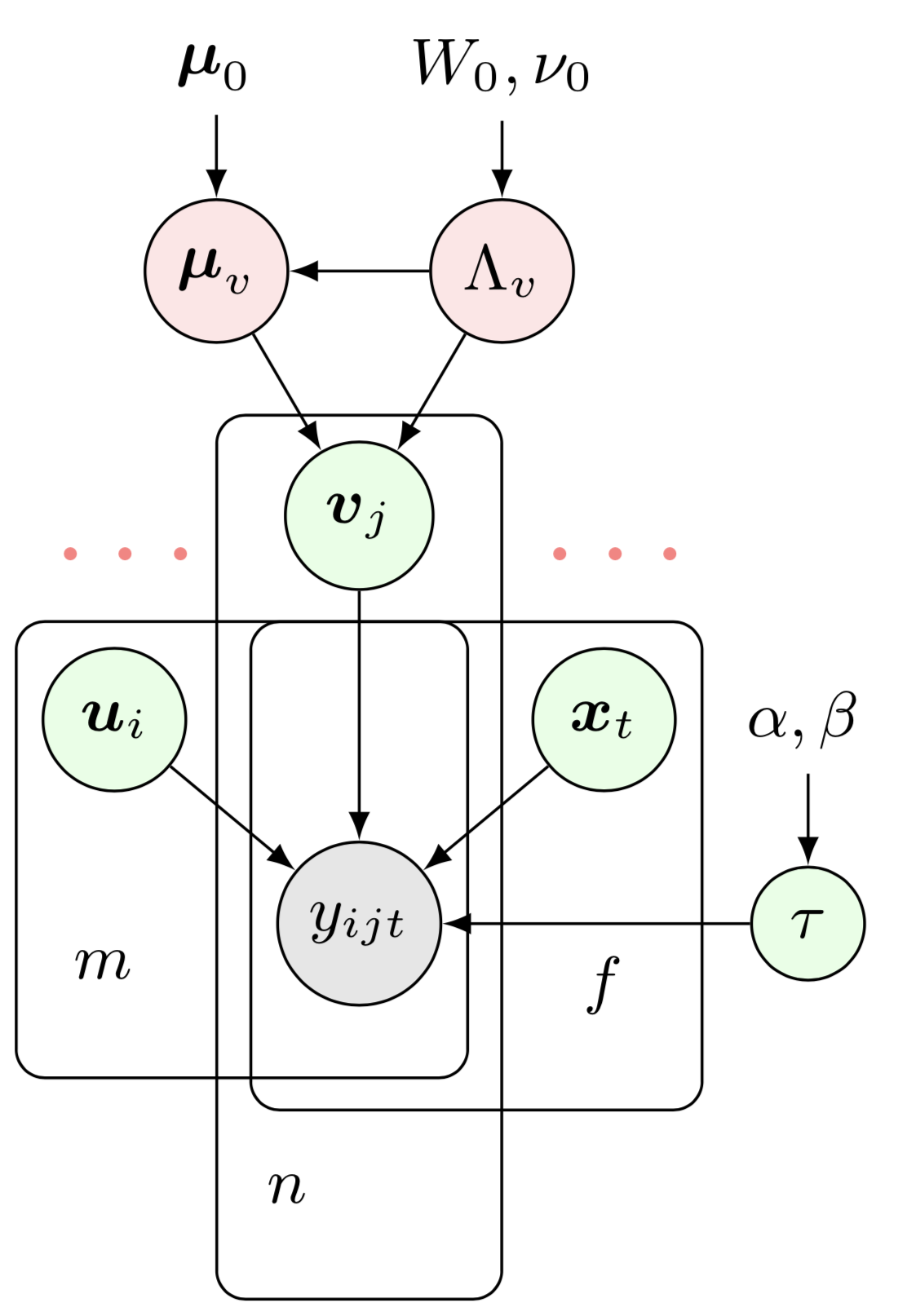Dies zeigt das Bayesian-Netzwerk des Bayesian Gaußschen CP-Faktorisierungsmodells (BGCP). Um dieses Beispiel für ein Bayes'sches Netzwerk zu zeichnen, müssen einige Vorbereitungen getroffen werden:

• preamble :
  1. Definieren Sie die documentclass als standalone , z. B. documentclass[border = 0.1cm]{standalone} mit 0,1 cm Rand,
  2. Verwenden Sie das Paket tikz , also usepackage{tikz} , und verwenden Sie tikz -Bibliothek wie usetikzlibrary{bayesnet} die ein wichtiges Werkzeug zum Zeichnen von Bayes'schen Netzwerken und gerichteten Faktorgraphen ist.
  3. Legen Sie den tikz -Stil mit dem Befehl tikzstyle{} fest.
  4. Verwenden Sie Umgebungen für mathematische Gleichungen, einschließlich usepackage{amsmath, amsfonts, amssymb} .
• body :
  1. Verwenden Sie begin{tikzpicture} end{tikzpicture} um mit dem Zeichnen zu beginnen.
  2. Verwenden Sie node , um Knoten und Textfelder im Bayes'schen Netzwerk zu definieren.
  3. Verwenden Sie path , um Pfeile im Bayes'schen Netzwerk zu definieren.
  4. Verwenden Sie plate um Platten im Bayes'schen Netzwerk zu definieren.

Bitte klicken Sie auf das Bild und sehen Sie sich den Quellcode an. Wenn Sie sich für das ursprüngliche Bayes'sche Netzwerk von BGCP im Artikel interessieren, schauen Sie sich bitte BGCP.tex an.

[Beispiel 3]

Dieses Beispiel stammt aus dem folgenden Artikel:

Xinyu Chen, Zhaocheng He, Yixian Chen, Yuhuan Lu, Jiawei Wang (2019). Imputation fehlender Verkehrsdaten und Mustererkennung mit einem Bayes'schen erweiterten Tensorfaktorisierungsmodell. Transportforschung Teil C: Emerging Technologies, 104: 66-77.

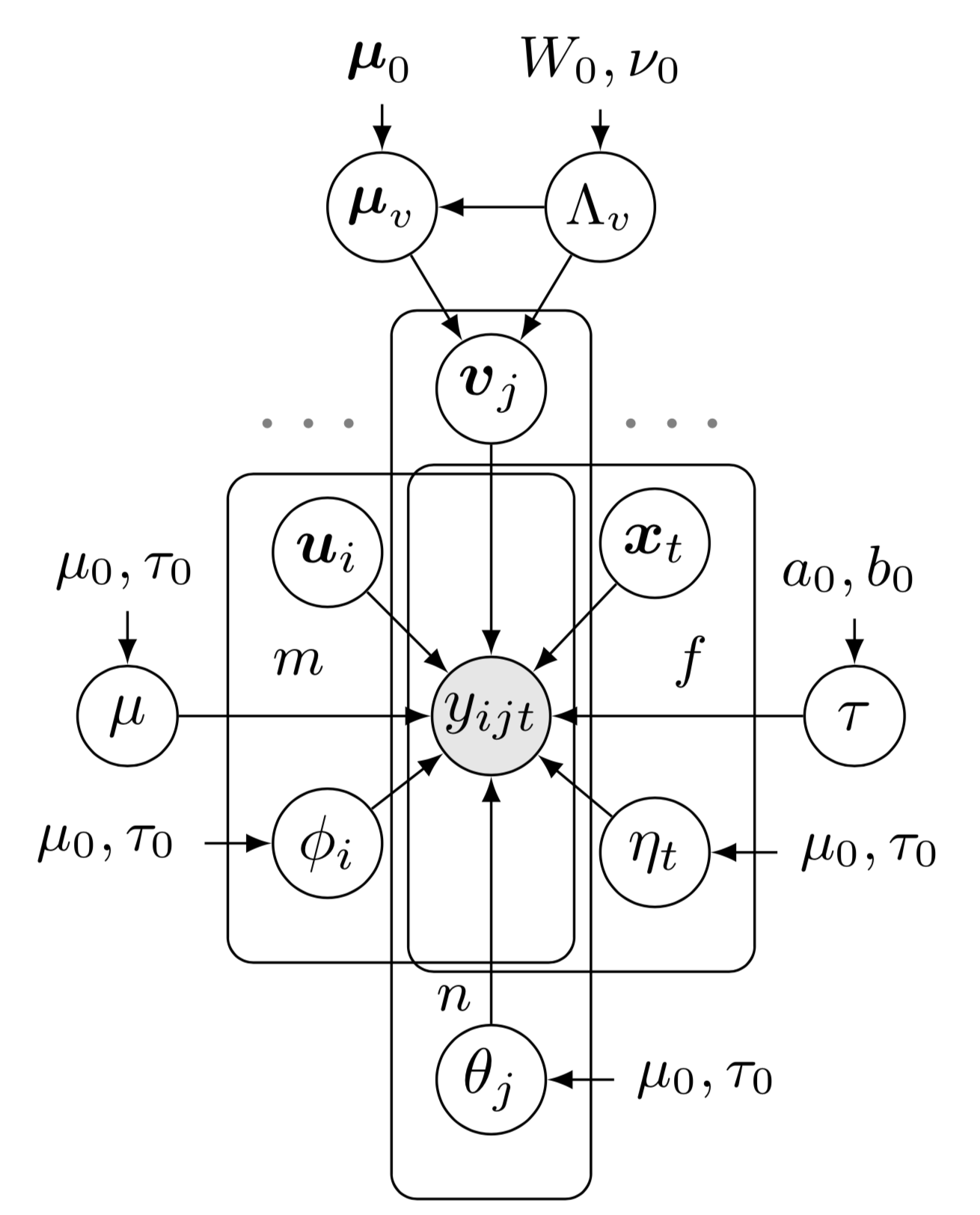Dies zeigt das Bayesianische Netzwerk des Bayesian Augmented Tensor Factorization (BATF)-Modells. Um dieses Beispiel für ein Bayes'sches Netzwerk zu zeichnen, müssen einige Vorbereitungen getroffen werden:

• preamble :
  1. Definieren Sie die documentclass als standalone , z. B. documentclass[border = 0.1cm]{standalone} mit 0,1 cm Rand,
  2. Verwenden Sie das Paket tikz , also usepackage{tikz} , und verwenden Sie tikz -Bibliothek wie usetikzlibrary{bayesnet} die ein wichtiges Werkzeug zum Zeichnen von Bayes'schen Netzwerken und gerichteten Faktorgraphen ist.
  3. Legen Sie den tikz -Stil mit dem Befehl tikzstyle{} fest.
  4. Verwenden Sie Umgebungen für mathematische Gleichungen, einschließlich usepackage{amsmath, amsfonts, amssymb} .
• body :
  1. Verwenden Sie begin{tikzpicture} end{tikzpicture} um mit dem Zeichnen zu beginnen.
  2. Verwenden Sie node , um Knoten und Textfelder im Bayes'schen Netzwerk zu definieren.
  3. Verwenden Sie path , um Pfeile im Bayes'schen Netzwerk zu definieren.
  4. Verwenden Sie plate um Platten im Bayes'schen Netzwerk zu definieren.

Bitte klicken Sie auf das Bild und sehen Sie sich den Quellcode an.

[Beispiel 4]

Dieses Beispiel stammt aus dem folgenden Artikel:

Xinyu Chen, Lijun Sun (2021). Bayesianische zeitliche Faktorisierung für mehrdimensionale Zeitreihenvorhersage. IEEE Transactions on Pattern Analysis and Machine Intelligence, 44 (9): 4659-4673.

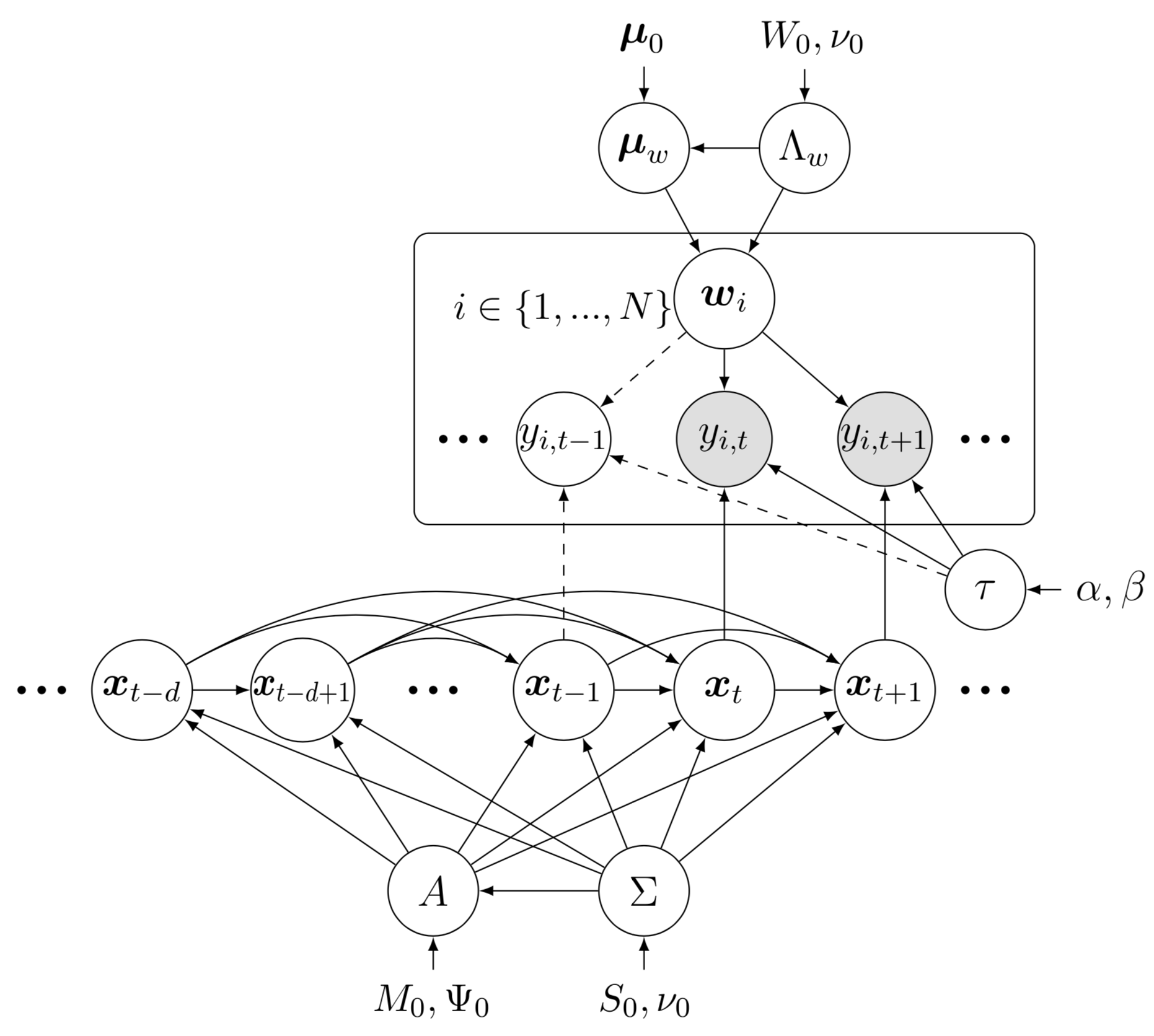Dies zeigt das Bayesianische Netzwerk des BTMF-Modells (Bayesian Temporal Matrix Factorization). Um dieses Beispiel für ein Bayes'sches Netzwerk zu zeichnen, müssen einige Vorbereitungen getroffen werden:

• preamble :
  1. Definieren Sie die documentclass als standalone , z. B. documentclass[border = 0.1cm]{standalone} mit 0,1 cm Rand,
  2. Verwenden Sie das Paket tikz , also usepackage{tikz} , und verwenden Sie tikz -Bibliothek wie usetikzlibrary{bayesnet} die ein wichtiges Werkzeug zum Zeichnen von Bayes'schen Netzwerken und gerichteten Faktorgraphen ist.
  3. Legen Sie den tikz -Stil mit dem Befehl tikzstyle{} fest.
  4. Verwenden Sie Umgebungen für mathematische Gleichungen, einschließlich usepackage{amsmath, amsfonts, amssymb} .
• body :
  1. Verwenden Sie begin{tikzpicture} end{tikzpicture} um mit dem Zeichnen zu beginnen.
  2. Verwenden Sie node , um Knoten und Textfelder im Bayes'schen Netzwerk zu definieren.
  3. Verwenden Sie path , um Pfeile im Bayes'schen Netzwerk zu definieren.
  4. Verwenden Sie plate um Platten im Bayes'schen Netzwerk zu definieren.

Bitte klicken Sie auf das Bild und sehen Sie sich den Quellcode an. Anstelle des multivariaten vektorautoregressiven Prozesses für zeitliche Faktoren können wir auch einen univariaten autoregressiven Prozess verwenden, um BTMF neu zu erstellen. Das Beyasian-Netzwerk ist unter btmf_net.png verfügbar. Sie können sich auch den Quellcode btmf_net.tex ansehen.

Grafische Modelle

[Beispiel 5]

Diese beiden Beispiele zeigen die teilweise beobachtete Zeitreihenmatrix bzw. den Tensor. Um beide Beispiele zu zeichnen, können wir die folgenden Schritte ausführen:

• preamble :

  1. Definieren Sie die documentclass als standalone .
  2. Benutze das Paket tikz .

• body :

  1. Verwenden Sie begin{tikzpicture} end{tikzpicture} um mit dem Zeichnen zu beginnen.
  2. Verwenden Sie node um Knoten und Textfelder im grafischen Modell zu definieren.
  3. Verwenden Sie path um Pfeile im grafischen Modell zu definieren.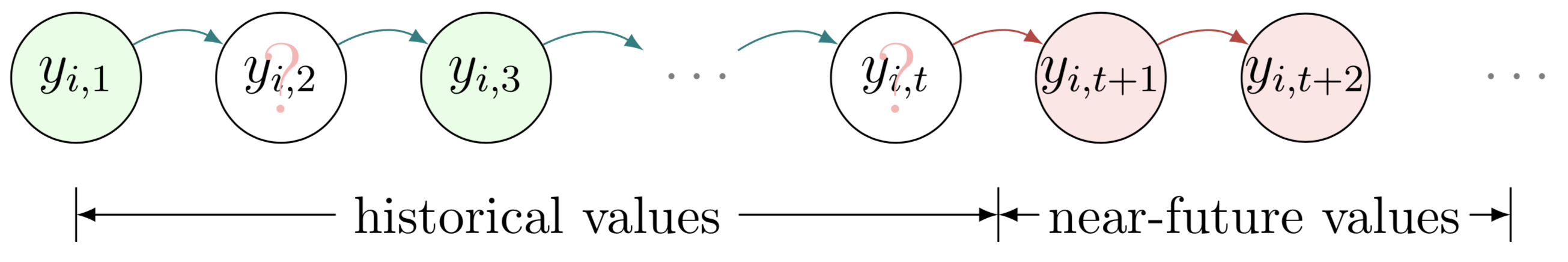

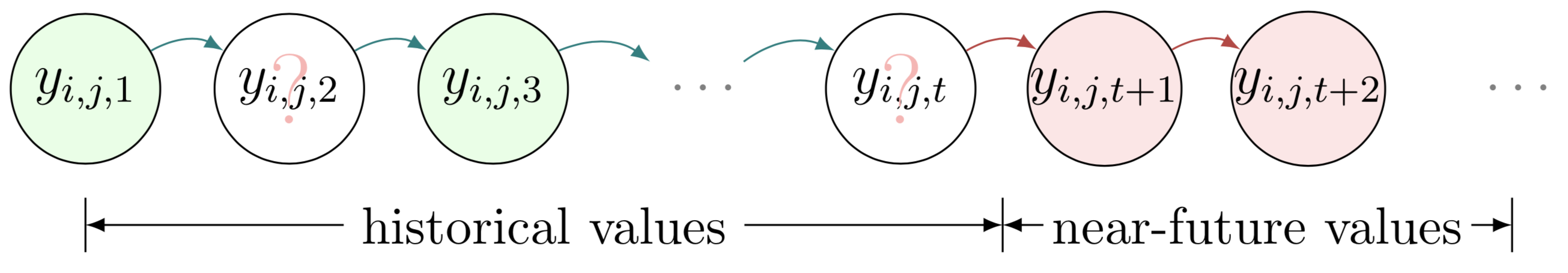
[Beispiel 6]

Diese beiden Beispiele zeigen die Zeitreihenvorhersage bei Vorhandensein fehlender Werte. Um beide Beispiele zu zeichnen, können wir die folgenden Schritte ausführen:

• preamble :

  1. Definieren Sie die documentclass als standalone .
  2. Benutze das Paket tikz .

• body :

  1. Verwenden Sie begin{tikzpicture} end{tikzpicture} um mit dem Zeichnen zu beginnen.
  2. Verwenden Sie node um Knoten und Textfelder im grafischen Modell zu definieren.
  3. Verwenden Sie path um Pfeile im grafischen Modell zu definieren.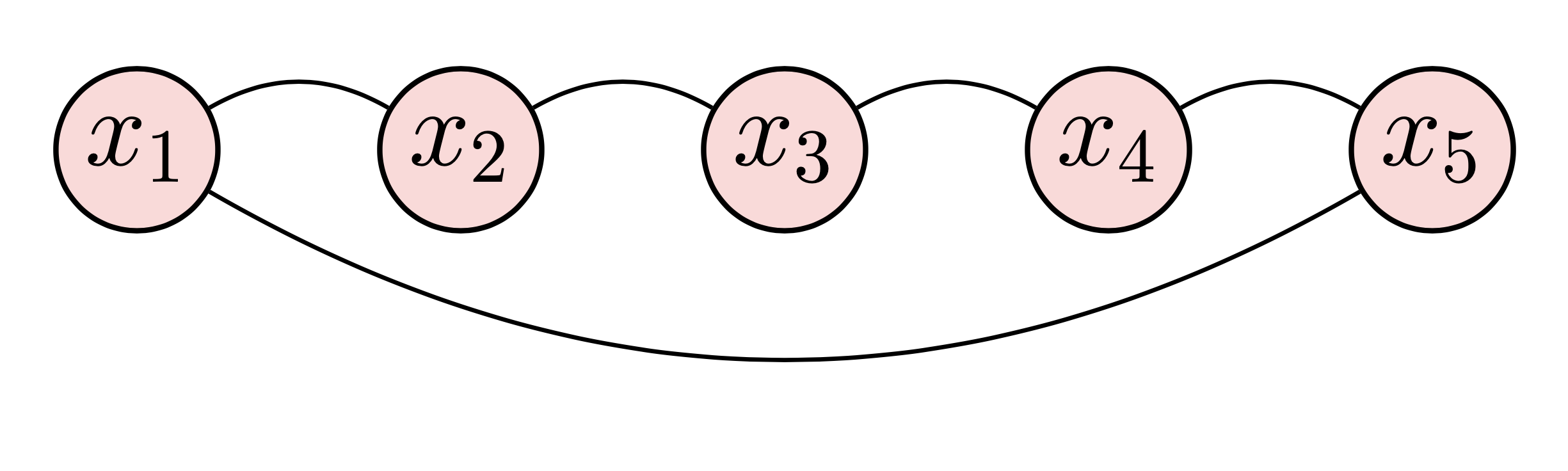

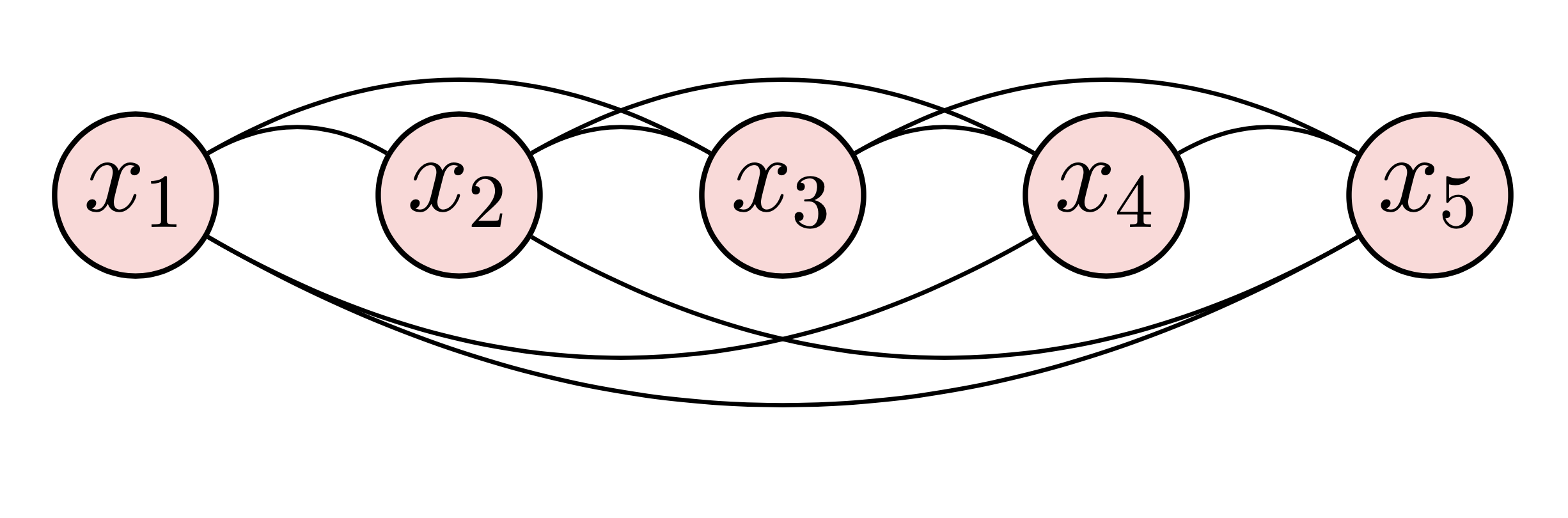
[Beispiel 7]

Diese beiden Beispiele zeigen die ungerichteten und zirkulierenden Graphen auf den relationalen Datenproben mit bestimmten Graden. Um beide Beispiele zu zeichnen, können wir die folgenden Schritte ausführen:

• preamble :

  1. Definieren Sie die documentclass als standalone .
  2. Benutze das Paket tikz .

• body :

  1. Verwenden Sie begin{tikzpicture} end{tikzpicture} um mit dem Zeichnen zu beginnen.
  2. Verwenden Sie node , um Knoten zu definieren.
  3. Verwenden Sie path um Pfeile zu definieren.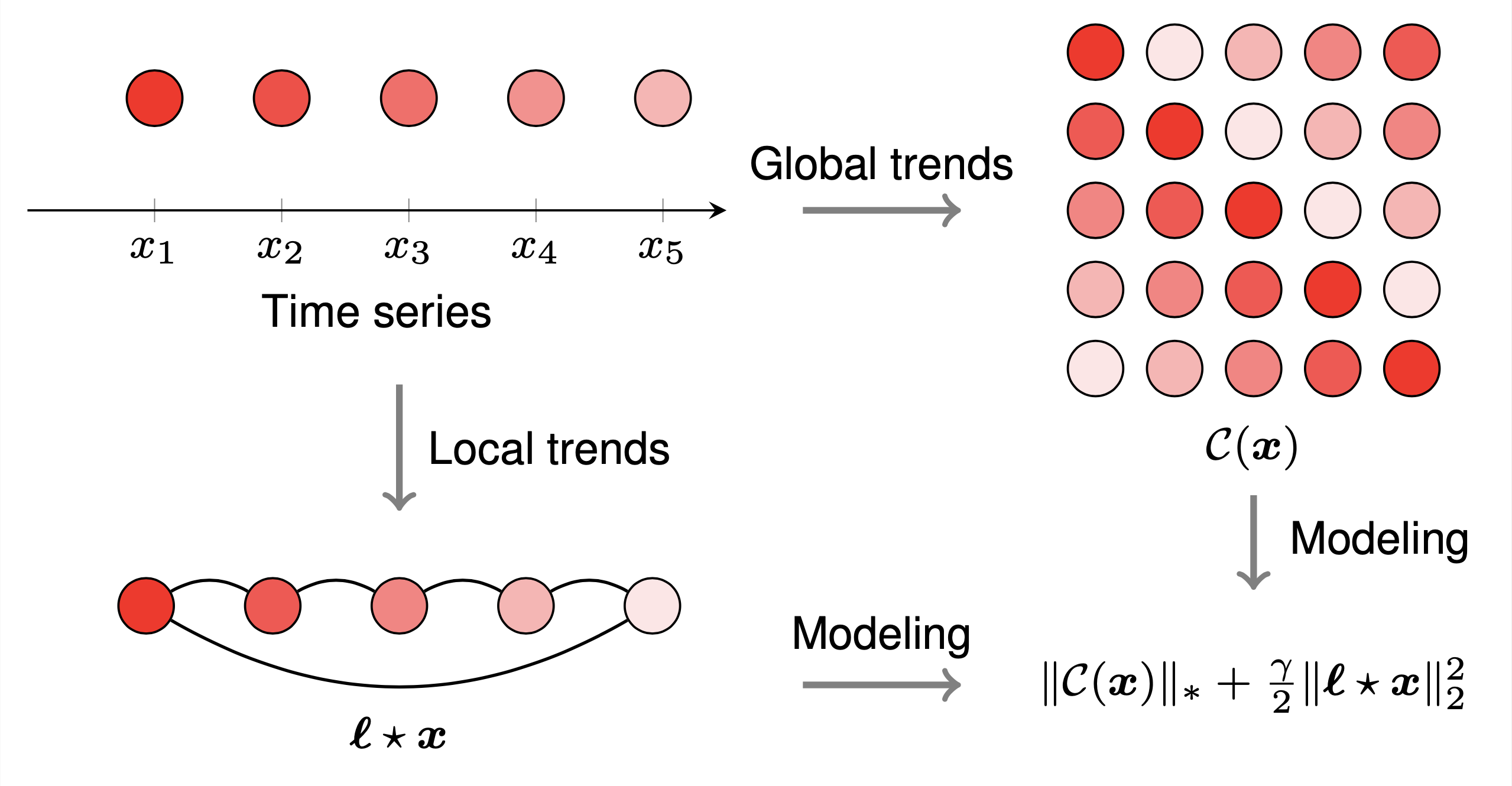

[Beispiel 8]

Dieses Beispiel stammt aus dem folgenden Artikel:

Xinyu Chen, Zhanhong Cheng, Nicolas Saunier, Lijun Sun (2022). Laplace-Faltungsdarstellung für die Imputation von Verkehrszeitreihen. arXiv-Vorabdruck arXiv: 2212.01529.

Dies gibt eine grafische Darstellung des Laplace-Faltungsmodells für die Zeitreihenimputation. Um das Beispiel zu zeichnen, können wir diesen Schritten folgen:

• preamble :
  1. Definieren Sie die documentclass als standalone .
  2. Benutze das Paket tikz .
• body :
  1. Verwenden Sie begin{tikzpicture} end{tikzpicture} um mit dem Zeichnen zu beginnen.
  2. Verwenden Sie begin{axis} end{axis} und addplot , um Koordinaten zu zeichnen,
  3. Verwenden Sie node und path um Knoten und Pfeile zu zeichnen.

pgfplots Funktionsdarstellung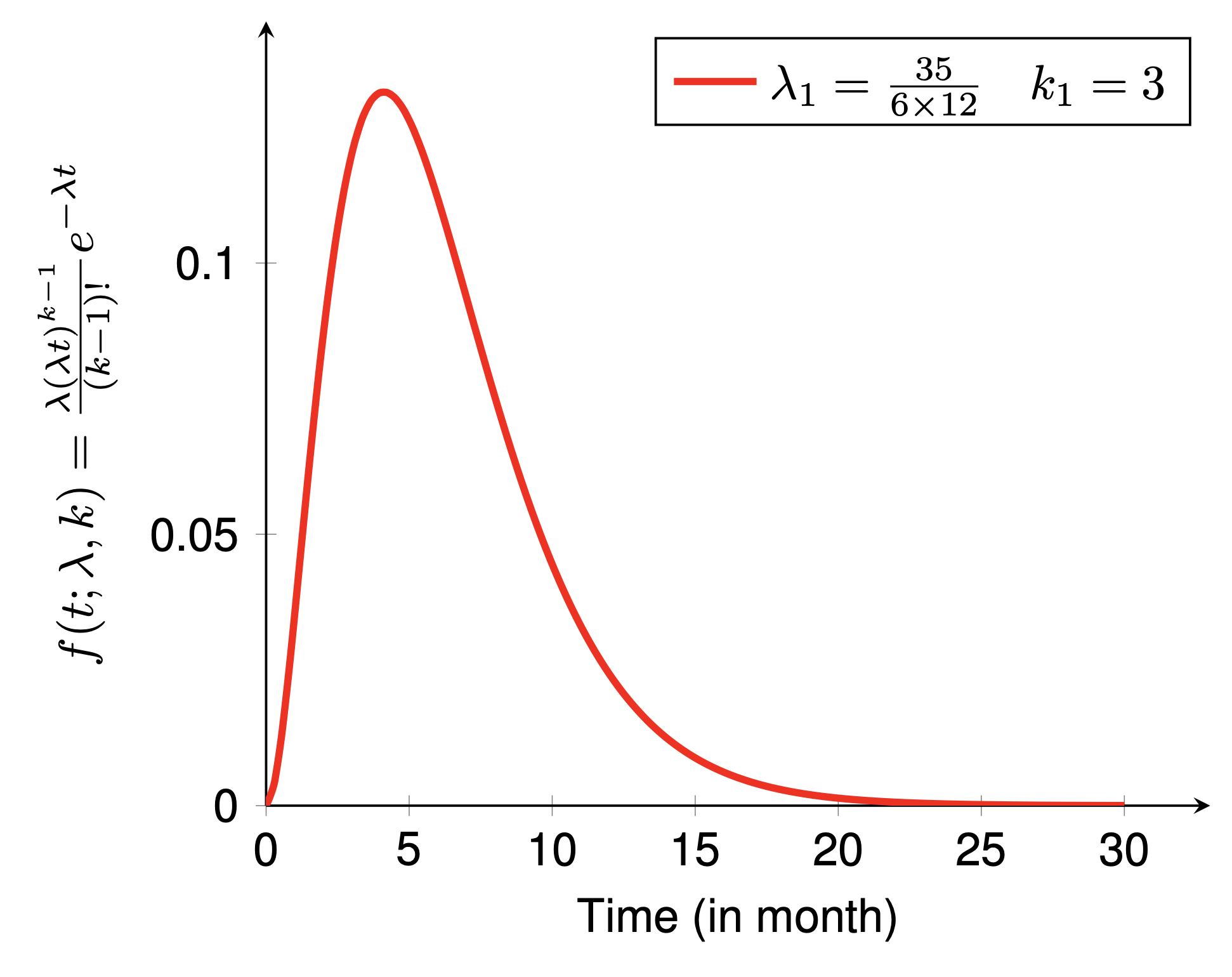

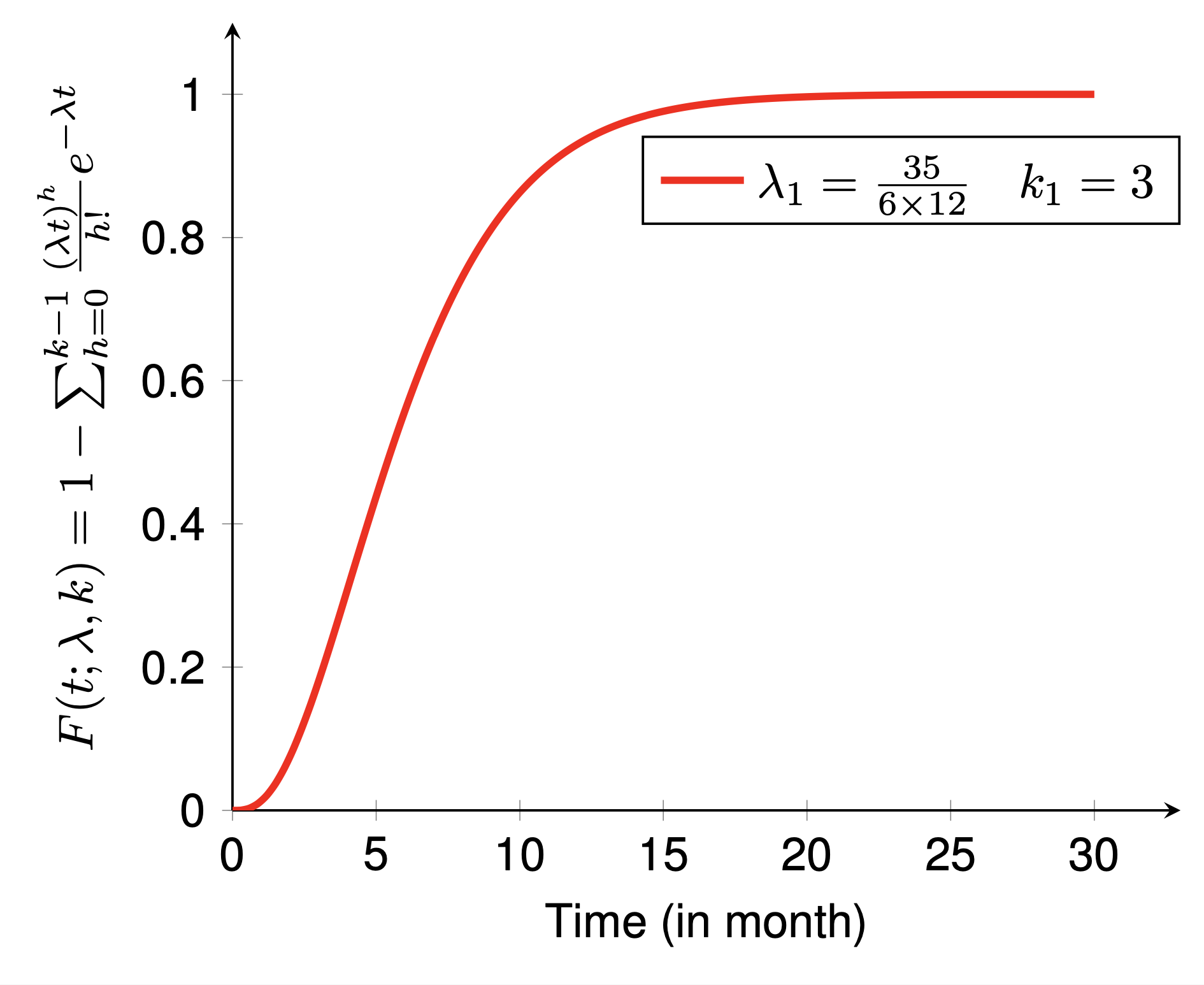
[Beispiel 9]

Diese beiden Beispiele zeigen die Wahrscheinlichkeitsdichtefunktion (PDF) bzw. die kumulative Dichtefunktion (CDF) der Erlang-Verteilung. Um das Beispiel zu zeichnen, müssen Sie einige Schritte befolgen:

• preamble :
  1. Definieren Sie die documentclass als standalone .
  2. Verwenden Sie das Paket pgfplots ,
  3. Legen Sie den Schriftstil fest und passen Sie pgfplotsset{} nach Ihren Wünschen an.
• body :
  1. Verwenden Sie begin{tikzpicture} end{tikzpicture} um mit dem Zeichnen zu beginnen.
  2. Verwenden Sie begin{axis} end{axis} um die Funktion zu zeichnen,
  3. Verwenden Sie addplot um die Funktion zum Zeichnen zu definieren.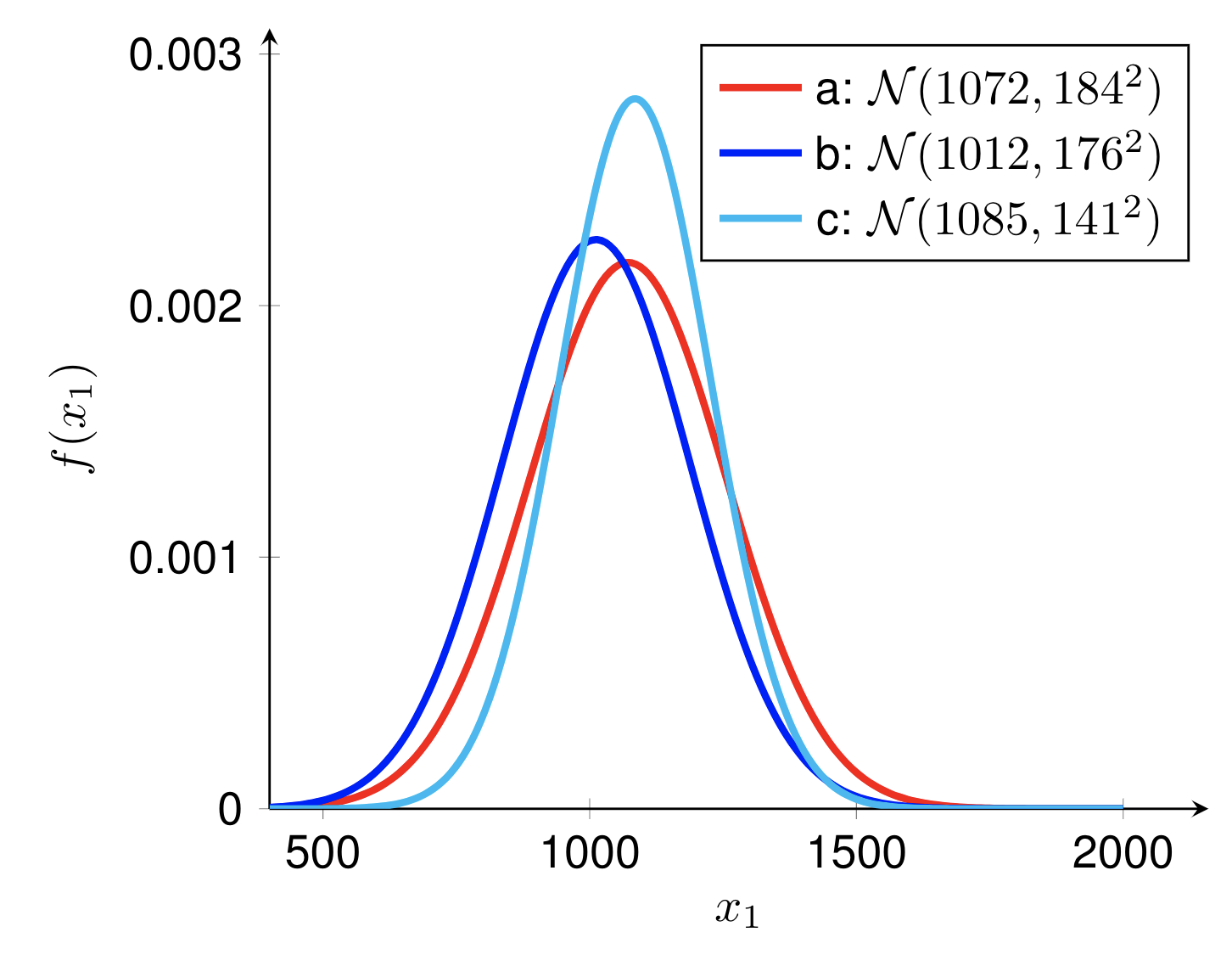

[Beispiel 10]

Dieses Beispiel zeigt das PDF der Normalverteilung mit unterschiedlichen Mittelwerten und Varianzen. Um dieses Beispiel zu zeichnen, müssen Sie einige Schritte befolgen:

• preamble :
  1. Definieren Sie die documentclass als standalone .
  2. Verwenden Sie das Paket pgfplots ,
  3. Legen Sie den Schriftstil fest und passen Sie pgfplotsset{} nach Ihren Wünschen an.
• body :
  1. Verwenden Sie pgfmathdeclarefunction , um die PDF-Funktion der Normalverteilung (Gaußverteilung) zu definieren.
  2. Verwenden Sie begin{tikzpicture} end{tikzpicture} um mit dem Zeichnen zu beginnen.
  3. Verwenden Sie begin{axis} end{axis} um die Funktion zu zeichnen,
  4. Verwenden Sie addplot um die Funktion zum Zeichnen zu definieren.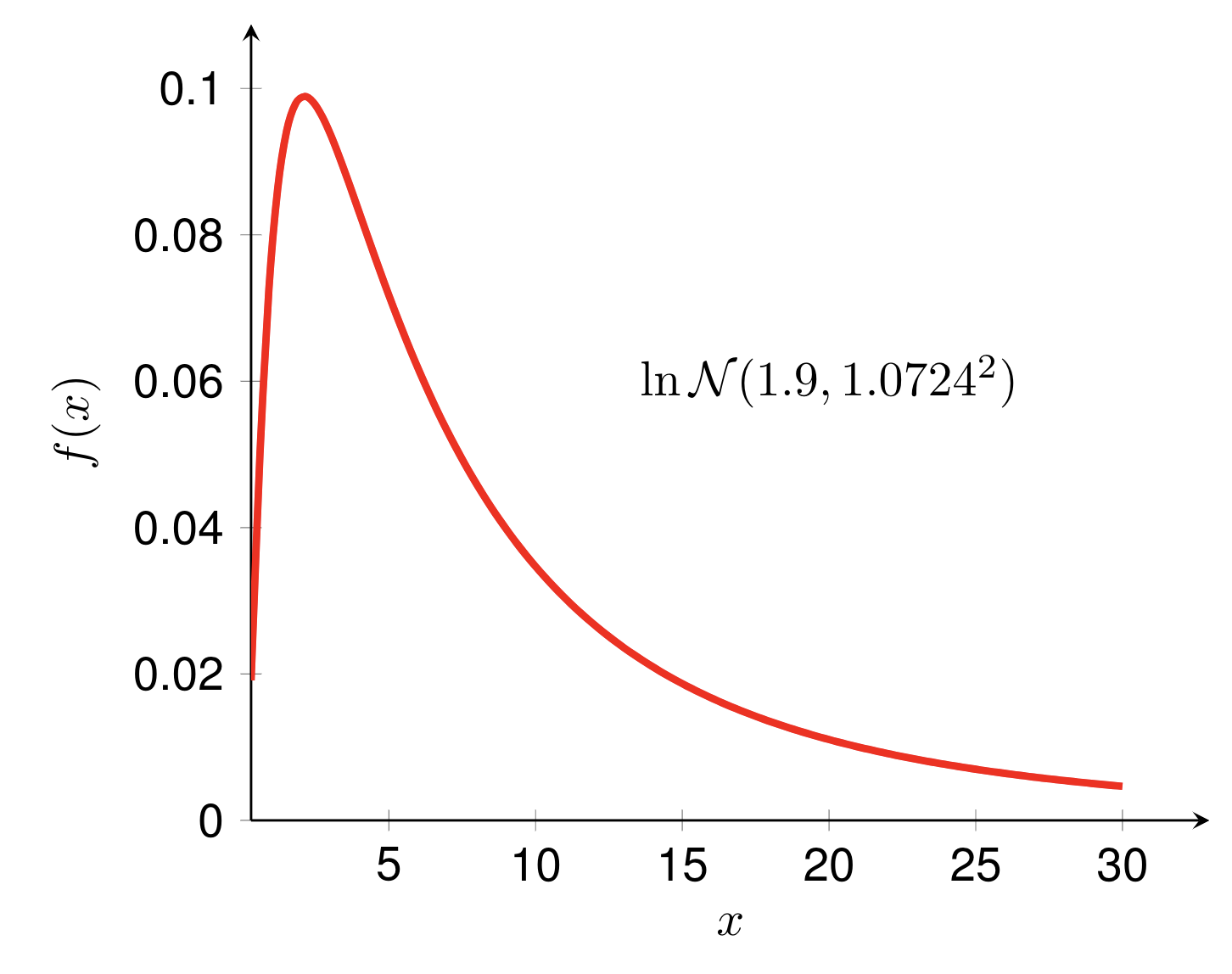
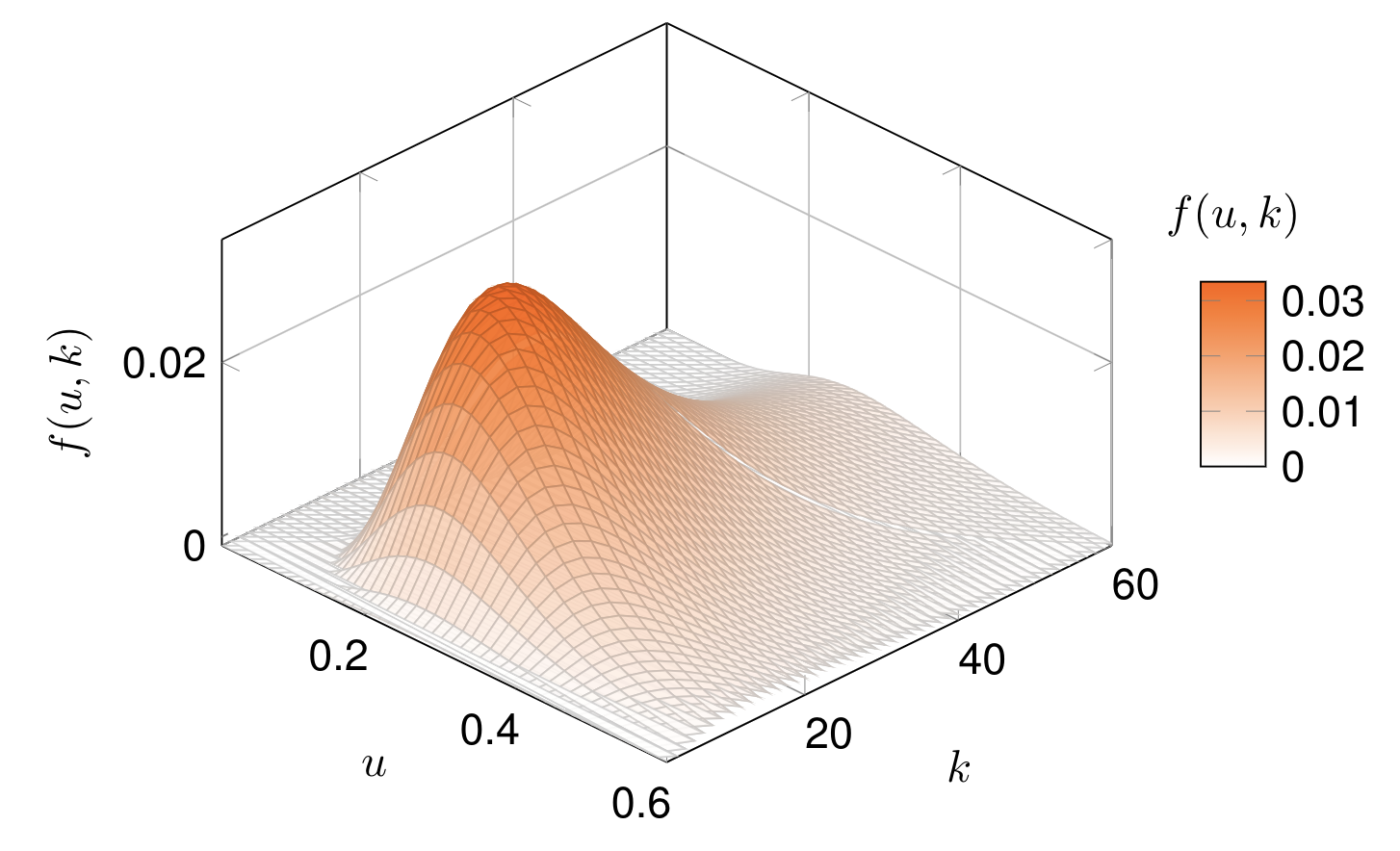
• Weitere Beiträge :
  1. Zeichnen der Normalverteilung in pgfplots
  2. Zahlenformat in der pgfplots-Achse
  3. Entfernen Sie die wissenschaftliche Notation, die unangemessen ist

[Beispiel 11]

Diese beiden Beispiele zeigen das PDF bzw. das gemeinsame PDF von Lognormalverteilungen. Es gibt einige empfohlene Materialien, um den Beispielen zu folgen:

• Weitere Beiträge :
  1. Zeichnen Sie eine bivariate Normalverteilung in TikZ
  2. Wie können zwei bivariate Normalverteilungen in einem Diagramm dargestellt werden?
  3. Zeichnen einer bivariaten Normalverteilung in Tikz
  4. Kurve mit addplot3 teilen

[Beispiel 12]

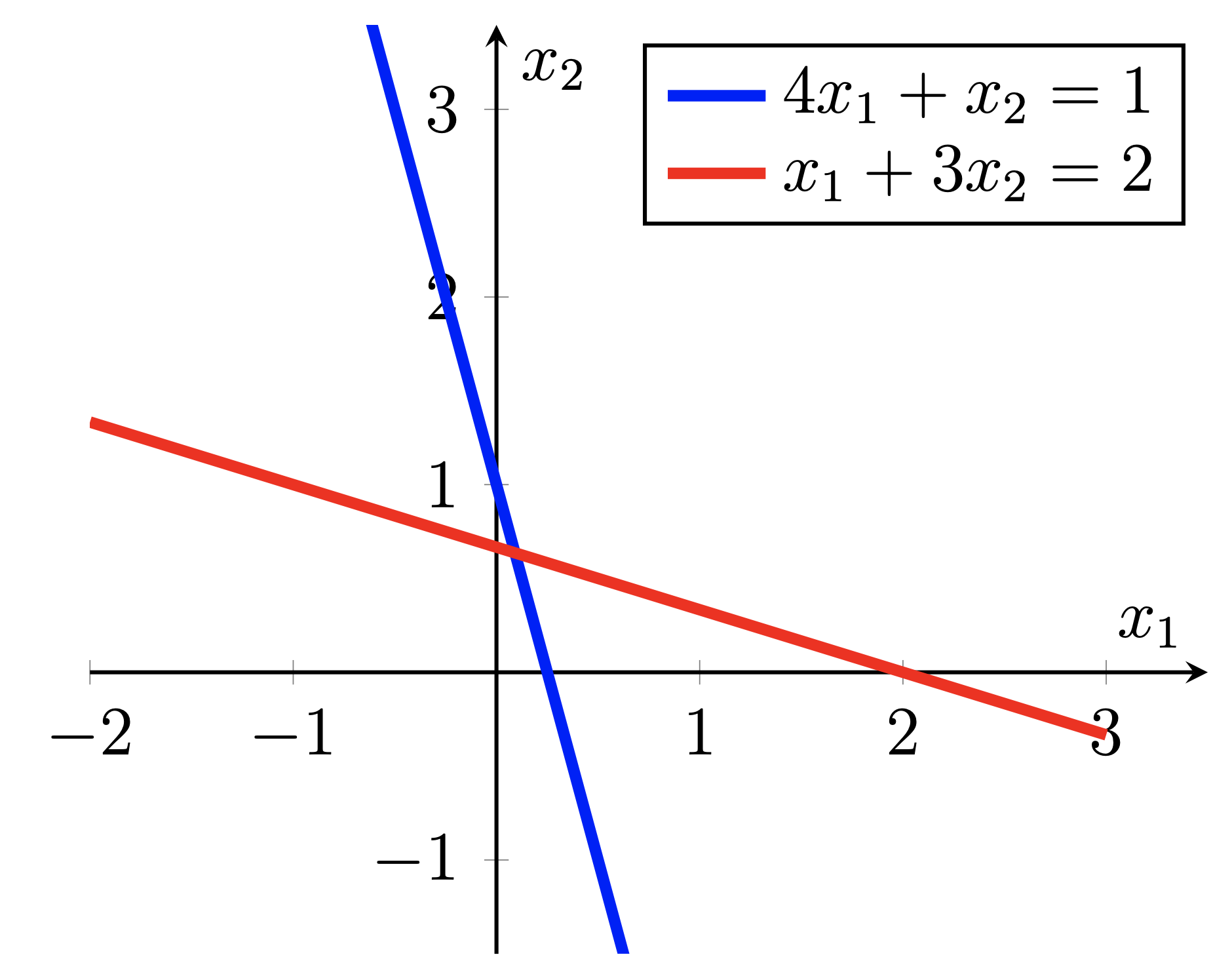
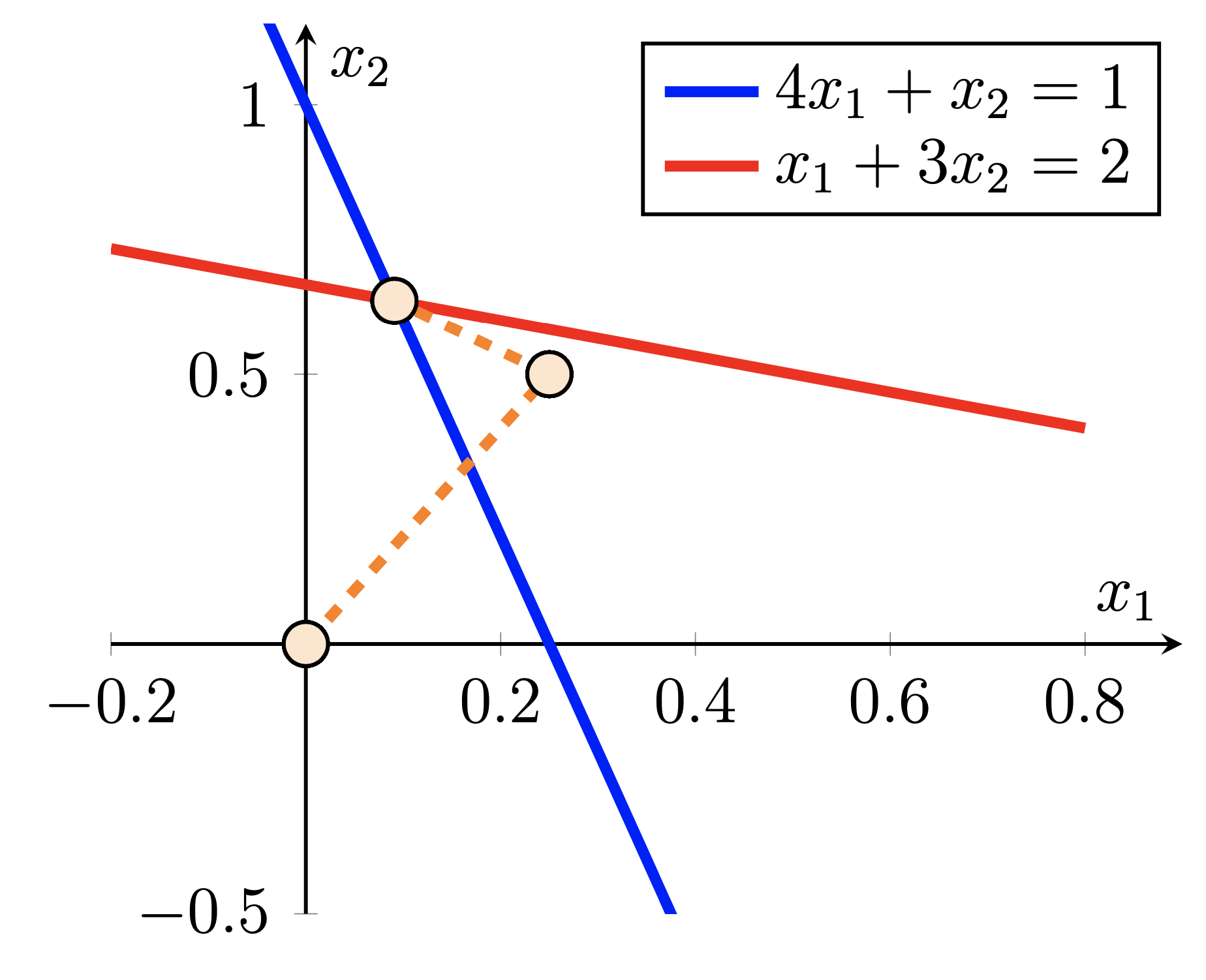
Diese beiden Beispiele zeigen den iterativen Prozess des konjugierten Gradienten zur Lösung eines linearen Gleichungssystems.

[Beispiel 13]

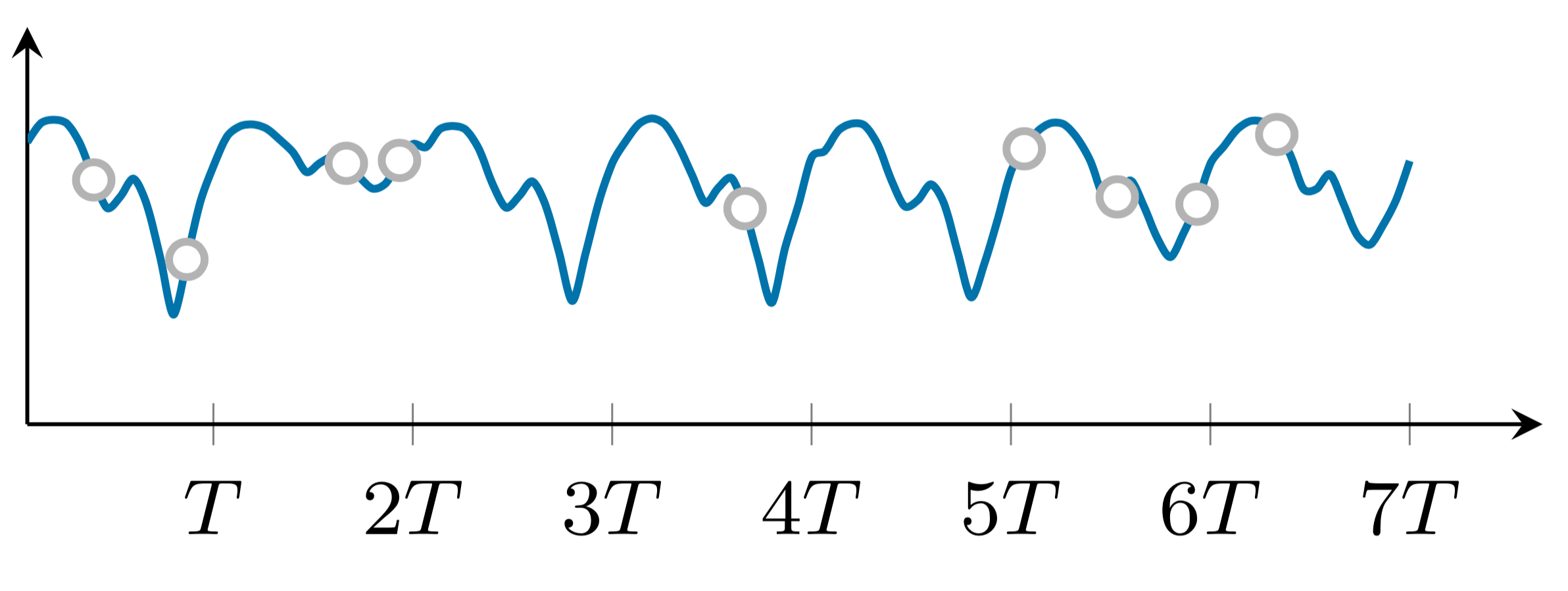
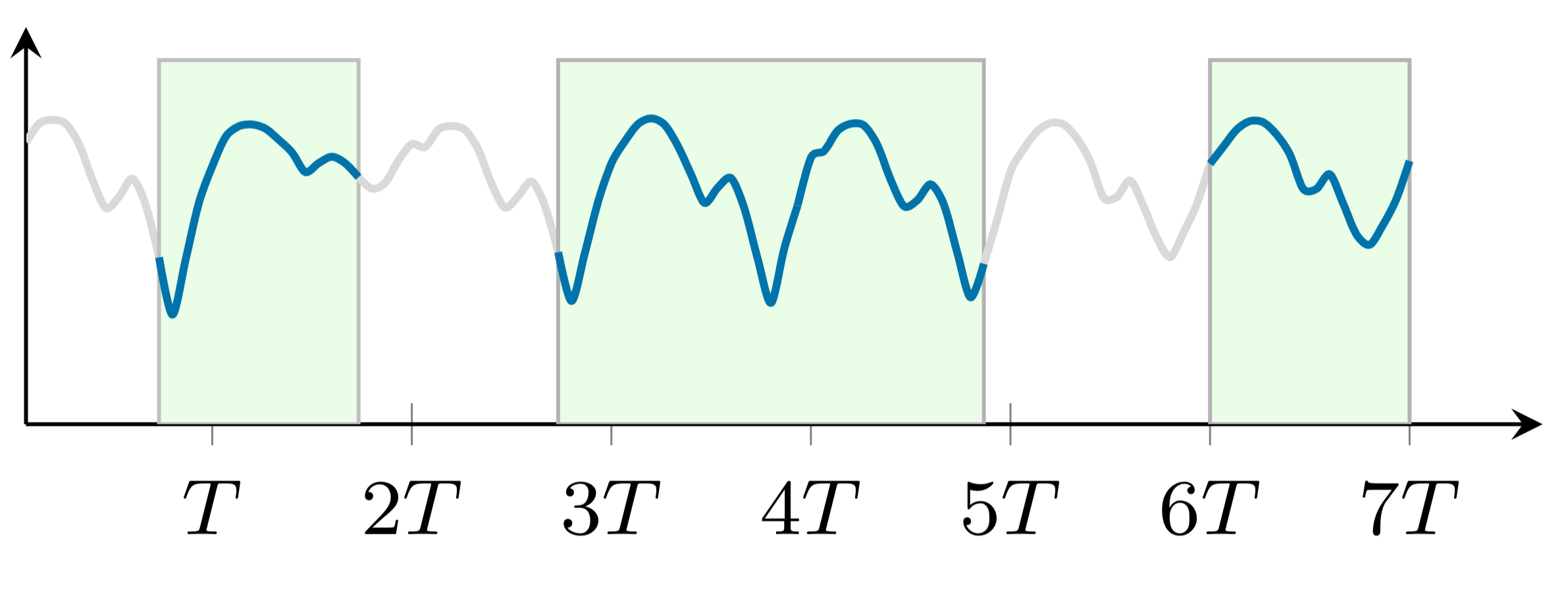
Diese beiden Beispiele zeigen die zufälligen und nicht zufälligen fehlenden Muster. Um beide Beispiele zu zeichnen, können wir die folgenden Schritte ausführen:

• preamble :
  1. Definieren Sie die documentclass als standalone .
  2. Verwenden Sie sowohl die Pakete tikz als auch pgfplots .
  3. Verwenden Sie begin{filecontents} end{filecontents} um die Daten einzuschließen.
• body :
  1. Verwenden Sie begin{tikzpicture} end{tikzpicture} um mit dem Zeichnen zu beginnen.
  2. Verwenden Sie begin{axis} end{axis} um die Funktion zu zeichnen,
  3. Verwenden Sie addplot um die Daten zu zeichnen.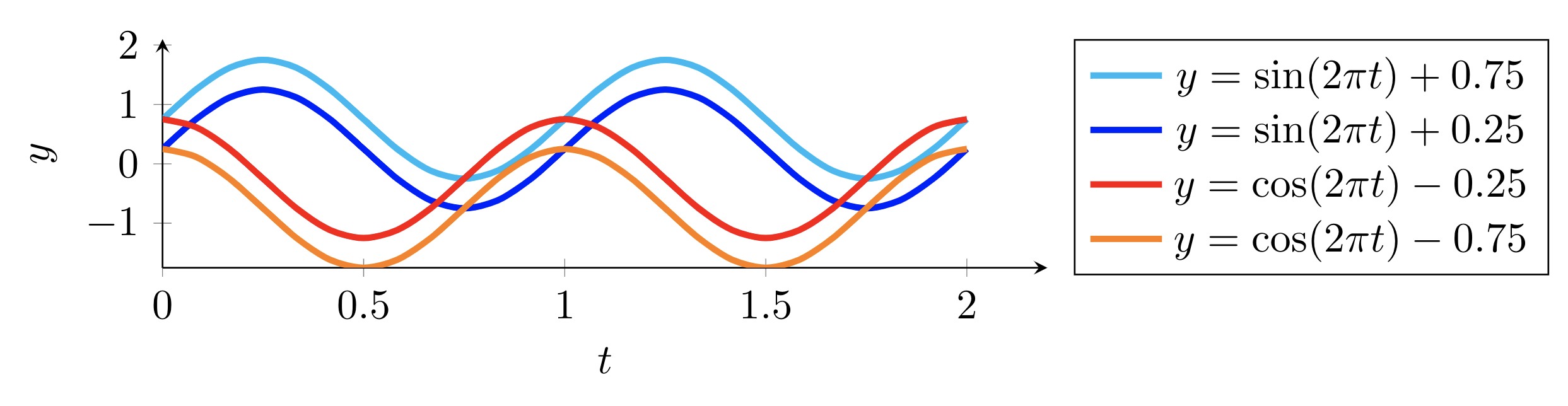

[Beispiel 14]

Dieses Beispiel zeigt vier Sequenzen bestehend aus Sinus- und Cosinusfunktionen. Wenn wir diese Sequenzen als Zeitreihen betrachten, können wir zwei Arten zeitlicher Dynamik erkennen, nämlich eine von der Sinusfunktion und eine andere von der Kosinusfunktion. Um dieses Beispiel zu zeichnen, können wir die folgenden Schritte ausführen:

• preamble :
  1. Definieren Sie die documentclass als standalone .
  2. Verwenden Sie das Paket pgfplots ,
  3. Legen Sie den Schriftstil fest und passen Sie pgfplotsset{} nach Ihren Wünschen an.
• body :
  1. Verwenden Sie pgfmathdeclarefunction , um die PDF-Funktion der Normalverteilung (Gaußverteilung) zu definieren.
  2. Verwenden Sie begin{tikzpicture} end{tikzpicture} um mit dem Zeichnen zu beginnen.
  3. Verwenden Sie begin{axis} end{axis} um die Funktion zu zeichnen,
  4. Verwenden Sie addplot um die Funktion zum Zeichnen zu definieren.

[Beispiel 15]

Dieses Beispiel veranschaulicht den Mechanismus der Zeitreihenvorhersage für Streaming-Daten in unserem Tracebase-Projekt. Um dieses Beispiel zu zeichnen, können wir die folgenden Schritte ausführen:

• preamble :
  1. Definieren Sie die documentclass als standalone .
  2. Verwenden Sie sowohl die Pakete tikz als auch pgfplots .
  3. Legen Sie den Schriftstil fest und passen Sie pgfplotsset{} nach Ihren Wünschen an.
• body :
  1. Verwenden Sie begin{tikzpicture} end{tikzpicture} um mit dem Zeichnen zu beginnen.
  2. Verwenden Sie begin{axis} end{axis} um die Grafik zu definieren.
  3. Verwenden Sie addplot um die Markierungen an einigen Koordinaten zu definieren und die Farbe dieser Markierungen anzugeben.

tikz für Matrixstruktur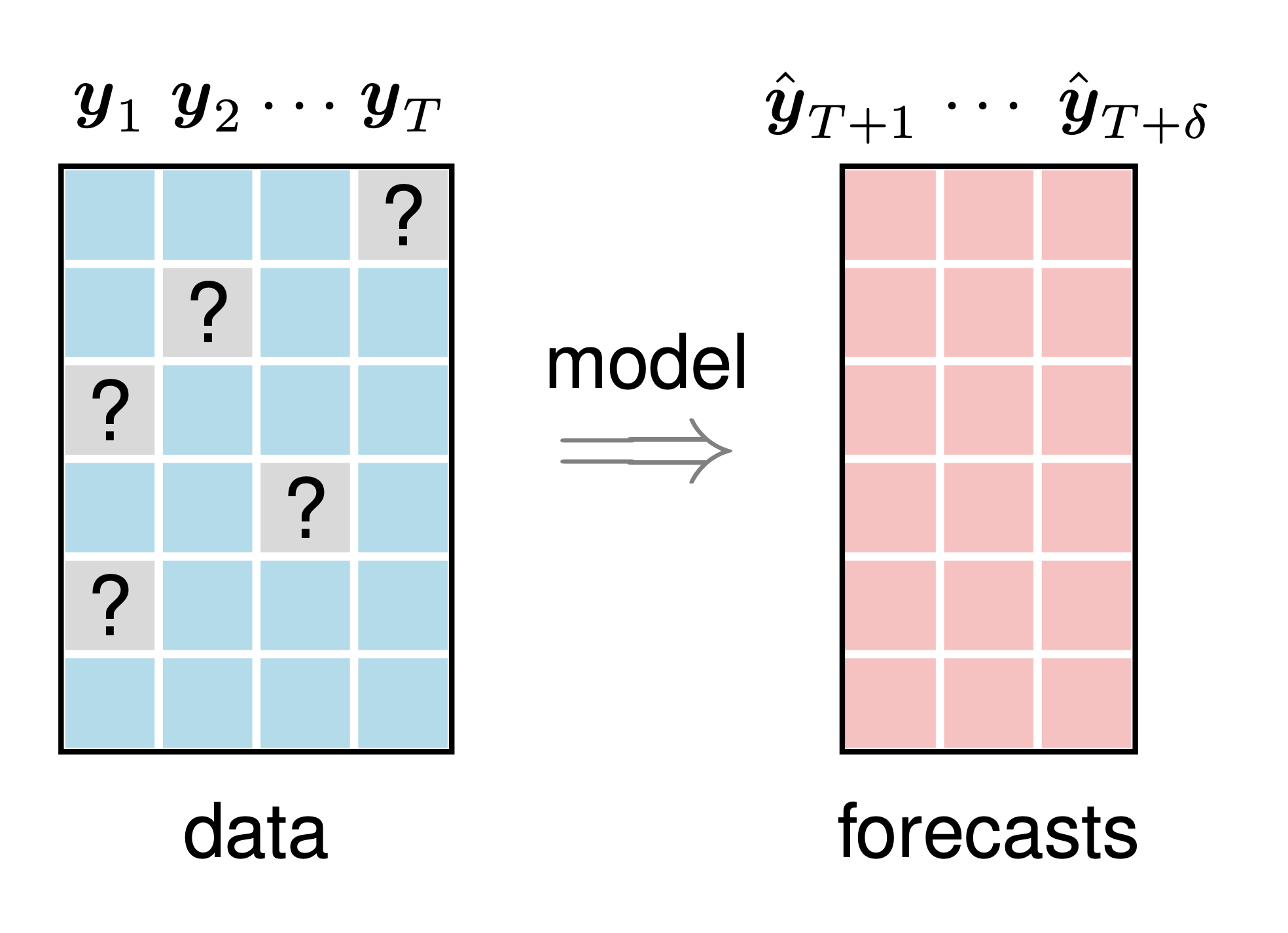

[Beispiel 16]

Dieses Beispiel veranschaulicht grafisch das Problem der multivariaten Zeitreihenvorhersage mit fehlenden Werten. Um dieses Beispiel zu zeichnen, können wir die folgenden Schritte ausführen:

• preamble :
  1. Definieren Sie die documentclass als standalone .
  2. Benutze das Paket tikz .
• body :
  1. Legen Sie die Parameter Depth , Width und Height mithilfe von newcommand fest.
  2. Verwenden Sie begin{tikzpicture} end{tikzpicture} um mit dem Zeichnen zu beginnen.
  3. Verwenden Sie die Befehle draw , filldraw und node um Rechtecke und Knoten zu definieren.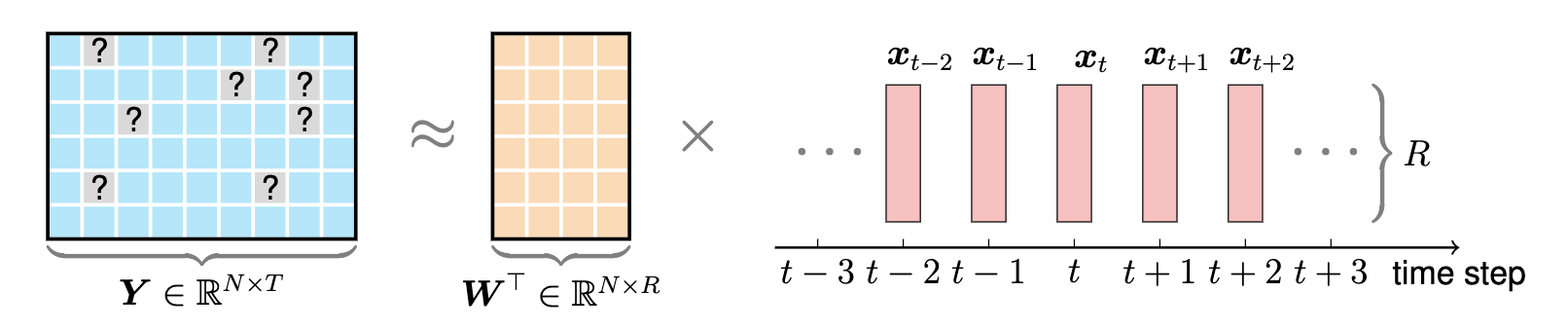

[Beispiel 17]

Dieses Beispiel veranschaulicht grafisch die zeitliche Matrixfaktorisierung. Um dieses Beispiel zu zeichnen, können wir die folgenden Schritte ausführen:

• preamble :
  1. Definieren Sie die documentclass als standalone .
  2. Benutze das Paket tikz .
• body :
  1. Verwenden Sie begin{tikzpicture} end{tikzpicture} um mit dem Zeichnen zu beginnen.
  2. Verwenden Sie draw und filldraw um Knoten und Rechtecke festzulegen.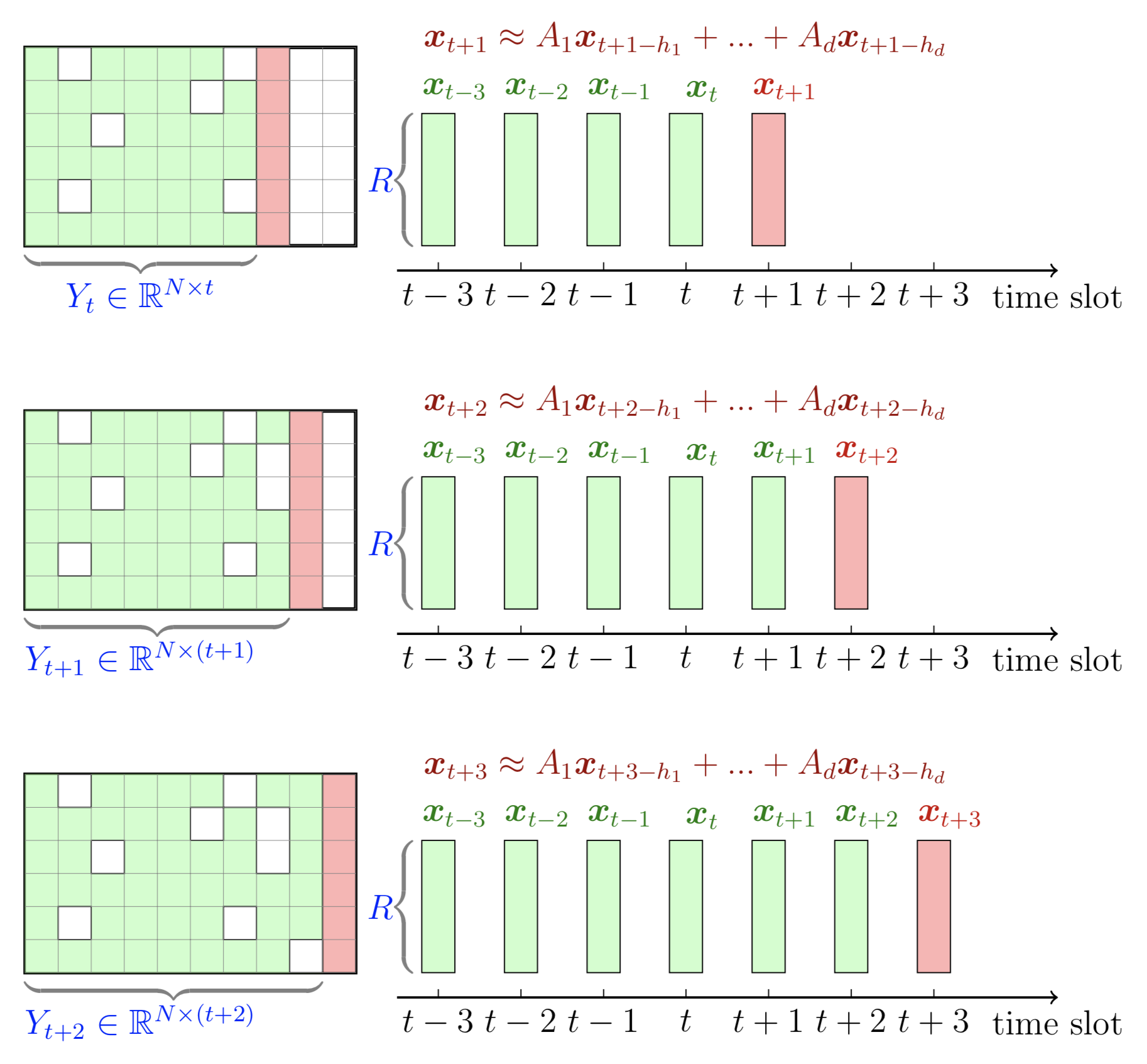

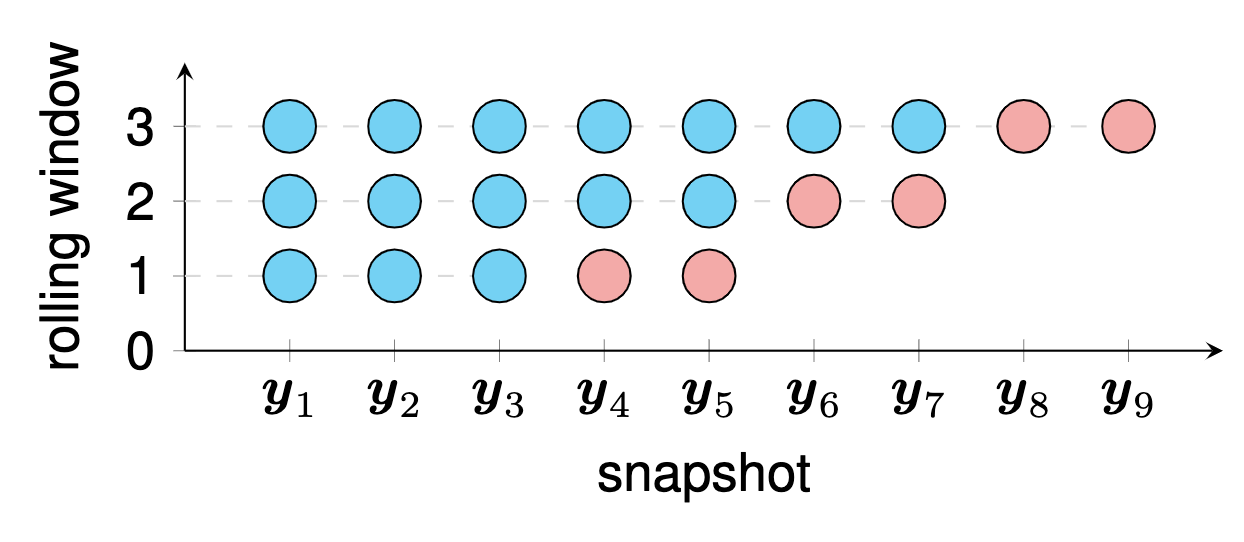
[Beispiel 18]

Dieses Beispiel zeigt eine grafische Darstellung der rollierenden Zeitreihenvorhersage mit zeitlicher Matrixfaktorisierung. Um dieses Beispiel zu zeichnen, können wir die folgenden Schritte ausführen:

• preamble :
  1. Definieren Sie die documentclass als standalone .
  2. Benutze das Paket tikz .
• body :
  1. Verwenden Sie begin{tikzpicture} end{tikzpicture} um mit dem Zeichnen zu beginnen.
  2. Verwenden Sie draw und filldraw um Knoten und Rechtecke festzulegen.

tikz-3dplot für Tensorstruktur

[Beispiel 19]

Dieses Beispiel zeigt eine grafische Darstellung eines Tensors dritter Ordnung. Um dieses Beispiel zu zeichnen, können wir die folgenden Schritte ausführen:

• preamble :
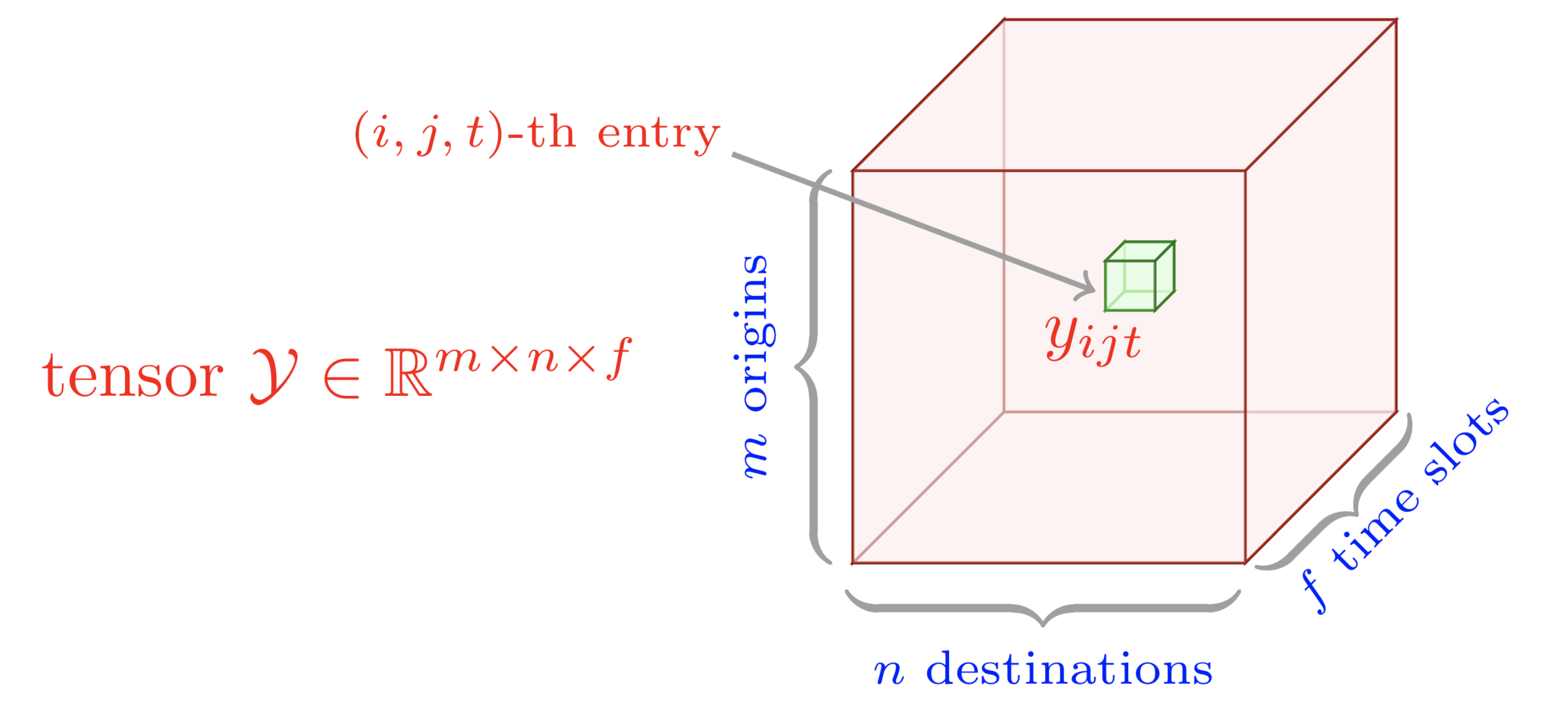
  1. Definieren Sie die documentclass als standalone .
  2. Verwenden Sie sowohl die Pakete tikz als auch tikz-3dplot .
• body :
  1. Legen Sie die Parameter Depth , Width und Height mithilfe von newcommand fest.
  2. Verwenden Sie begin{tikzpicture} end{tikzpicture} um mit dem Zeichnen zu beginnen.
  3. Definieren Sie die Koordinaten der Tensorkanten,
  4. Verwenden Sie den Befehl draw um Knoten zu definieren.

[Beispiel 20]

Dieses Beispiel veranschaulicht grafisch die klassische CP-Tensorfaktorisierung auf einem Tensor dritter Ordnung. Um dieses Beispiel zu zeichnen, können wir die folgenden Schritte ausführen:

• preamble :
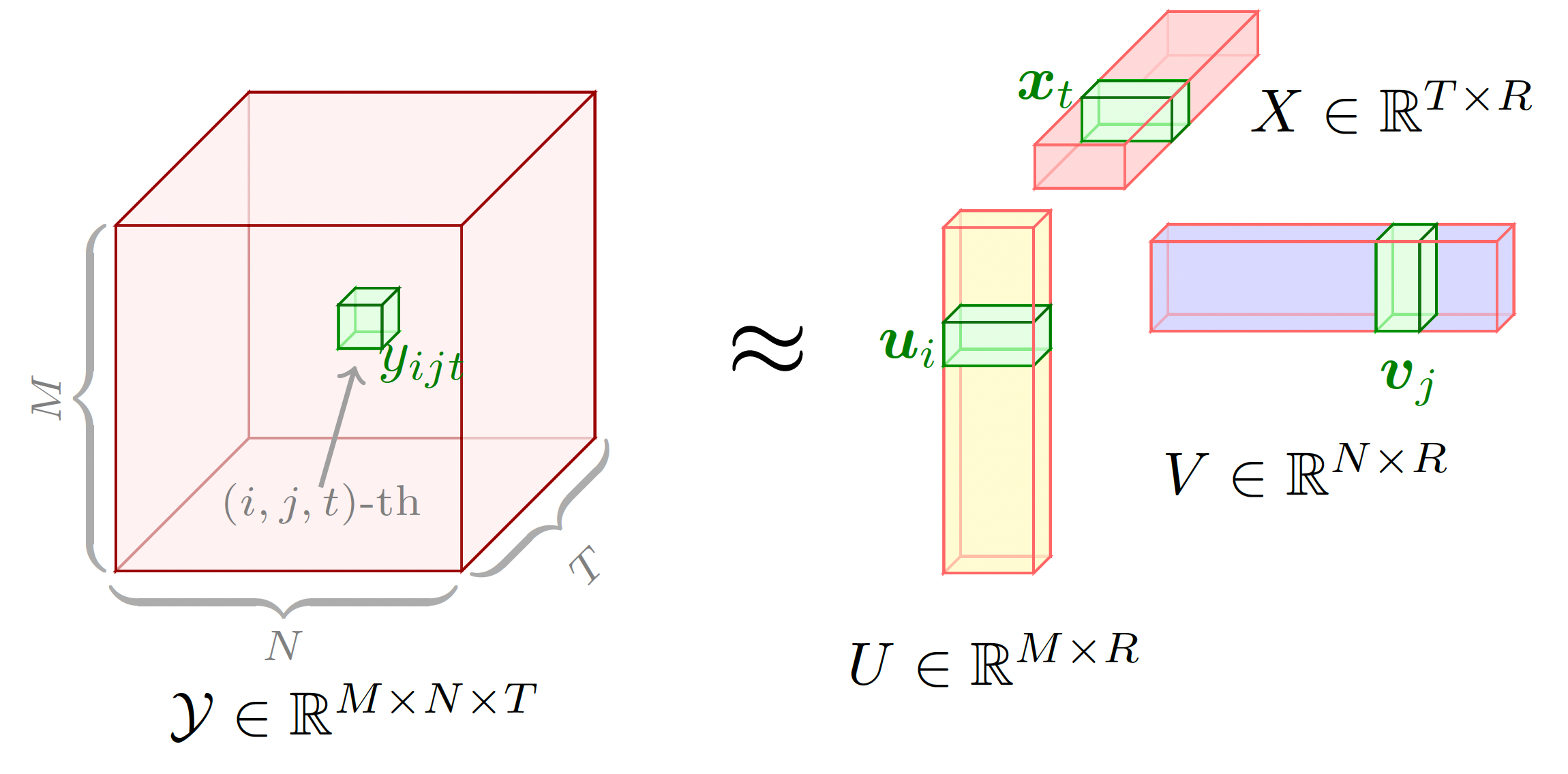
  1. Definieren Sie die documentclass als standalone .
  2. Verwenden Sie sowohl die Pakete tikz als auch tikz-3dplot .
• body :
  1. Legen Sie die Parameter Depth , Width und Height mithilfe von newcommand fest.
  2. Verwenden Sie begin{tikzpicture} end{tikzpicture} um mit dem Zeichnen zu beginnen.
  3. Definieren Sie die Koordinaten der Tensorkanten,
  4. Verwenden Sie den Befehl draw um Knoten zu definieren.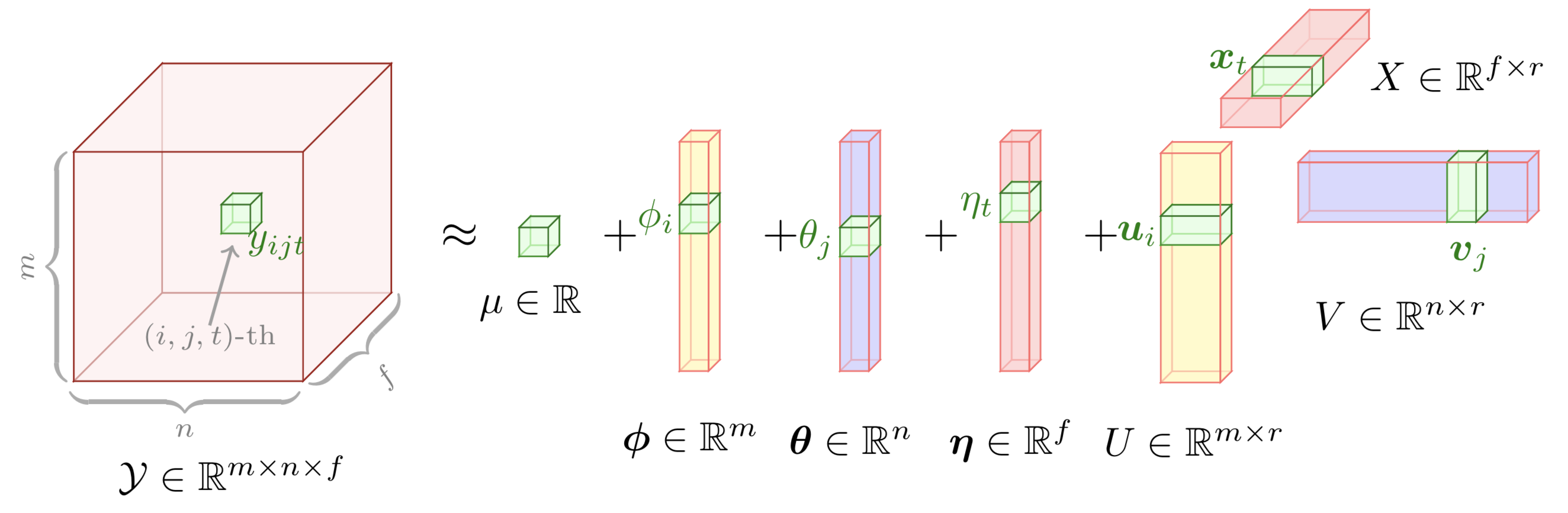

[Beispiel 21]

Dieses Beispiel zeigt eine grafische Darstellung des erweiterten Tensorfaktorisierungsmodells. Um dieses Beispiel zu zeichnen, können wir die folgenden Schritte ausführen:

• preamble :
  1. Definieren Sie die documentclass als standalone .
  2. Verwenden Sie sowohl die Pakete tikz als auch tikz-3dplot .
• body :
  1. Legen Sie die Parameter Depth , Width und Height mithilfe von newcommand fest.
  2. Verwenden Sie begin{tikzpicture} end{tikzpicture} um mit dem Zeichnen zu beginnen.
  3. Definieren Sie die Koordinaten der Tensorkanten,
  4. Verwenden Sie den Befehl draw um Knoten zu definieren.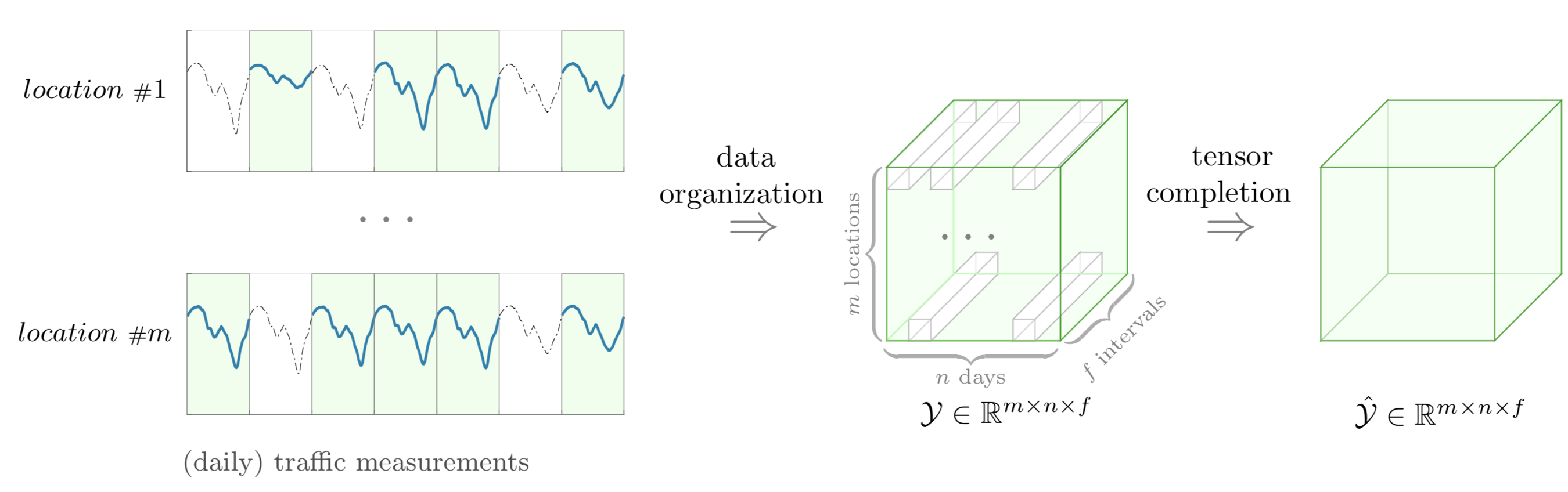

[Beispiel 22]

Dieses Beispiel zeigt eine grafische Darstellung der Tensor-Vervollständigungsaufgabe und ihres Rahmenwerks, einschließlich der Datenorganisation und Tensor-Vervollständigung, wobei Verkehrsmessungen teilweise beobachtet werden. Um dieses Beispiel zu zeichnen, können wir die folgenden Schritte ausführen:

• Anfrage :
  1. Kurve1.pdf hochladen,
  2. Kurve2.pdf hochladen.
• preamble :
  1. Definieren Sie die documentclass als standalone .
  2. Verwenden Sie sowohl die Pakete tikz als auch tikz-3dplot .
• body :
  1. Legen Sie die Parameter Depth , Width und Height mithilfe von newcommand fest.
  2. Verwenden Sie begin{tikzpicture} end{tikzpicture} um mit dem Zeichnen zu beginnen.
  3. Definieren Sie die Koordinaten der Tensorkanten,
  4. Verwenden Sie den Befehl draw um Knoten zu definieren.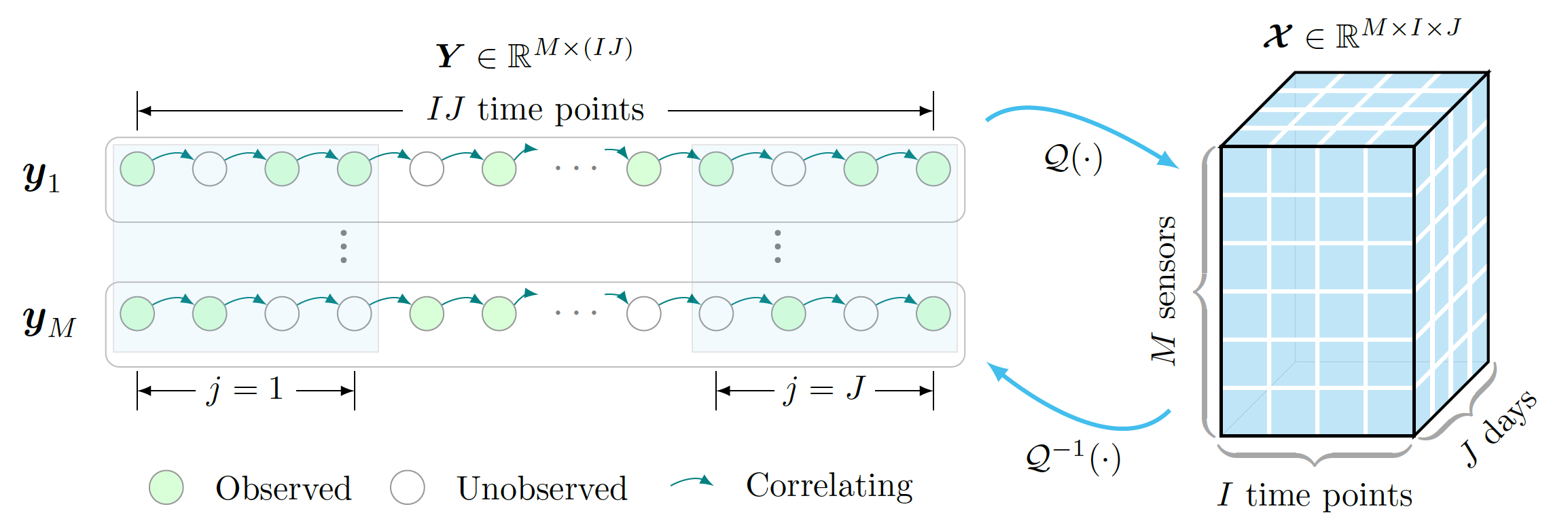

[Beispiel 23]

Dieses Beispiel zeigt grafisch das autoregressive Tensor-Vervollständigungsmodell mit niedrigem Rang. Um dieses Beispiel zu zeichnen, können wir die folgenden Schritte ausführen:

• preamble :
  1. Definieren Sie die documentclass als standalone .
  2. Verwenden Sie sowohl die Pakete tikz als auch tikz-3dplot .
• body :
  1. Legen Sie die Parameter Depth , Width und Height mithilfe von newcommand fest.
  2. Verwenden Sie begin{tikzpicture} end{tikzpicture} um mit dem Zeichnen zu beginnen.
  3. Verwenden Sie die Befehle node , path plate um Knoten, Pfeile und Platten zu definieren.
  4. Definieren Sie die Koordinaten der Tensorkanten,
  5. Verwenden Sie den Befehl draw um Knoten zu definieren.

[Beispiel 24]

Dieses Beispiel zeigt grafisch den Singulärwert-Schwellenwertprozess der Tensordaten mit einheitlicher Transformation. Um dieses Beispiel zu zeichnen, können wir die folgenden Schritte ausführen:

• preamble :
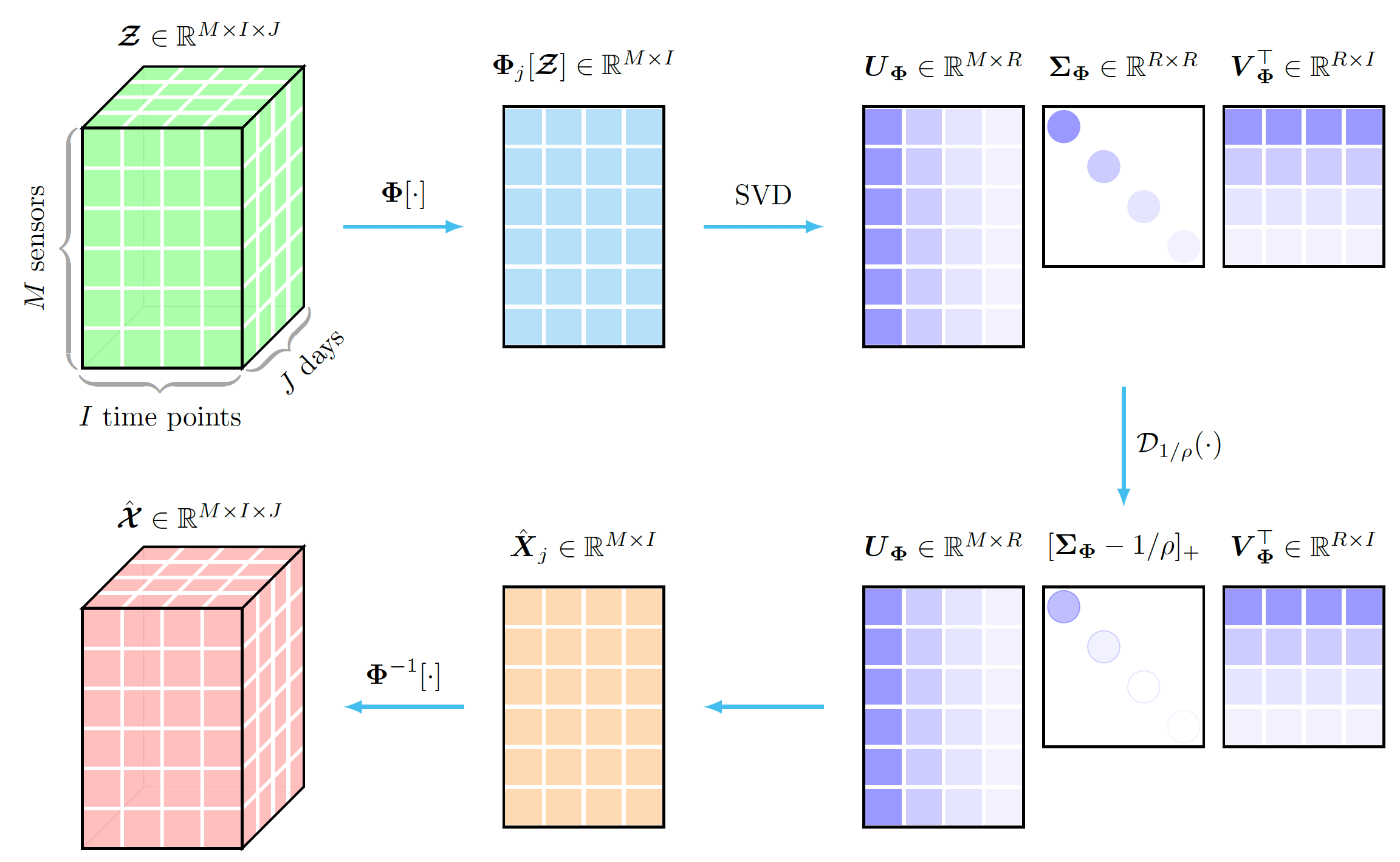
  1. Definieren Sie die documentclass als standalone .
  2. Verwenden Sie sowohl die Pakete tikz als auch tikz-3dplot .
• body :
  1. Legen Sie die Parameter Depth , Width und Height mithilfe von newcommand fest.
  2. Verwenden Sie begin{tikzpicture} end{tikzpicture} um mit dem Zeichnen zu beginnen.
  3. Verwenden Sie den Befehl node , um Knoten zu definieren.
  4. Definieren Sie die Koordinaten der Tensorkanten,
  5. Verwenden Sie den Befehl draw , um Knoten zu definieren.
  6. Verwenden Sie den Befehl filldraw um die Farben von Rechtecken zu definieren.

[Beispiel 25]

Dieses Beispiel zeigt eine grafische Darstellung des Tensor-Vervollständigungsmodells mit niedrigem Rang. Um dieses Beispiel zu zeichnen, können wir die folgenden Schritte ausführen:

• Anfrage :
  1. input_tensor.pdf hochladen,
  2. Laden Sie „output_tensor.pdf“ hoch.
• preamble :
  1. Definieren Sie die documentclass als standalone .
  2. Verwenden Sie sowohl die Pakete tikz als auch tikz-3dplot .
  3. Verwenden Sie das algorithm2e Paket.
  4. Verwenden Sie usetikzlibrary{positioning, matrix, fit, calc} .
• body :
  1. Verwenden Sie die Umgebung begin{algorithm} end{algorithm} , um den Algorithmus zu definieren.
  2. Verwenden Sie den Befehl matrix , um die Komponenten zu positionieren.
  3. Verwenden Sie begin{scope} end{scope} um die Ebenen einzuschließen.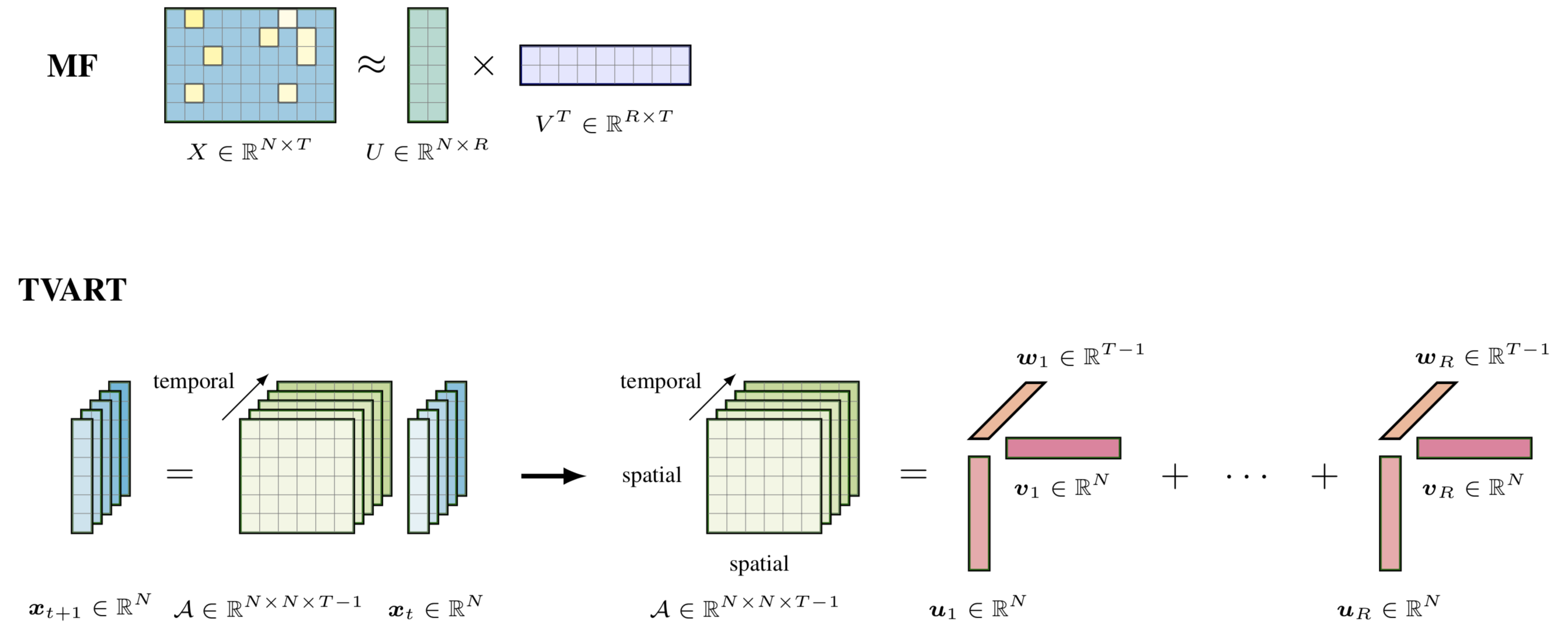

[Beispiel 26]

Dieses Beispiel zeigt eine grafische Darstellung des Tensor-Regressionsmodells mit niedrigem Rang. Um dieses Beispiel zu zeichnen, können wir die folgenden Schritte ausführen:

• preamble :
  1. Definieren Sie die documentclass als standalone .
  2. Verwenden Sie sowohl die Pakete tikz als auch tikz-3dplot .
• body :
  1. Legen Sie die Parameter Depth , Width und Height mithilfe von newcommand fest.
  2. Verwenden Sie begin{tikzpicture} end{tikzpicture} um mit dem Zeichnen zu beginnen.
  3. Verwenden Sie den Befehl draw um Knoten zu definieren.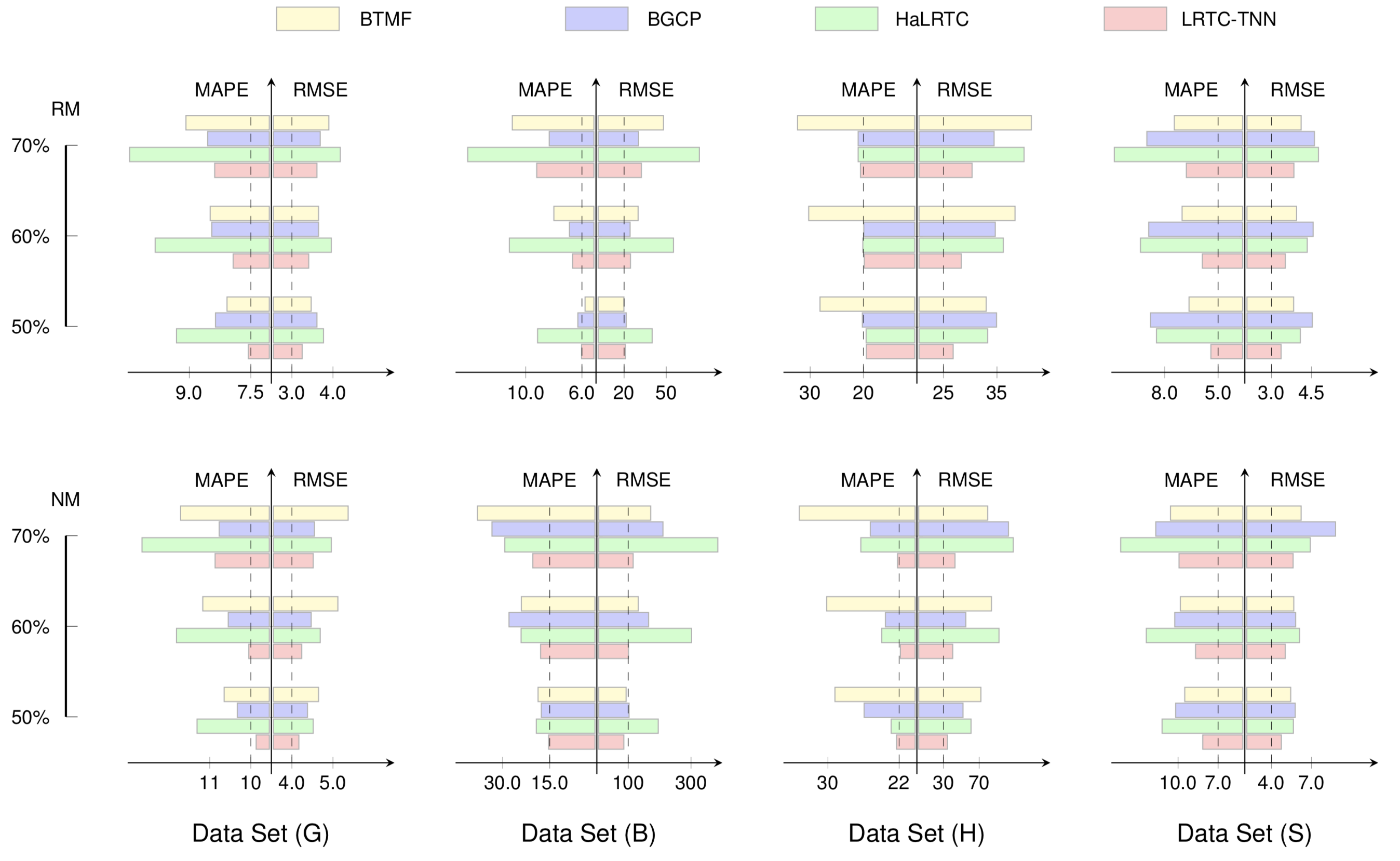

Datenvisualisierung

[Beispiel 27]

Dieses Beispiel zeigt die Imputationsgenauigkeit einiger Matrix- und Tensormodelle. Um dieses Beispiel zu zeichnen, können wir die folgenden Schritte ausführen:

• preamble :
  1. Definieren Sie die documentclass als standalone .
  2. Benutze das Paket tikz .
• body :
  1. Verwenden Sie begin{tikzpicture} end{tikzpicture} um mit dem Zeichnen zu beginnen.
  2. Verwenden Sie den Befehl draw , um Knoten zu definieren.
  3. Verwenden Sie den Befehl pgfuseimage um Bilder zu importieren.

Verwandte Projekte

• tikz-bayesnet
• genial-tikz
• transdim

Veröffentlichungen

Die meisten dieser Beispiele stammen aus unseren Arbeiten:

• Xinyu Chen, Zhanhong Cheng, HanQin Cai, Nicolas Saunier, Lijun Sun (2024). Laplace-Faltungsdarstellung für die Imputation von Verkehrszeitreihen . IEEE Transactions on Knowledge and Data Engineering, 36 (11): 6490-6502. [Vorabdruck] [DOI] [Folien] [Daten & Python-Code]

• Xinyu Chen, Lijun Sun (2022). Bayesianische zeitliche Faktorisierung für mehrdimensionale Zeitreihenvorhersage . IEEE Transactions on Pattern Analysis and Machine Intelligence, 44 (9): 4659-4673. [Vorabdruck] [DOI] [Folien] [Daten & Python-Code]

• Xinyu Chen, Mengying Lei, Nicolas Saunier, Lijun Sun (2022). Autoregressive Tensorvervollständigung mit niedrigem Rang für die Imputation von raumzeitlichen Verkehrsdaten . IEEE Transactions on Intelligent Transportation Systems, 23 (8): 12301-12310. [Preprint] [DOI] [Daten & Python-Code] (Auch teilweise für den MiLeTS-Workshop von KDD 2021 akzeptiert, siehe Workshop-Papier)

• Xinyu Chen, Yixian Chen, Nicolas Saunier, Lijun Sun (2021). Skalierbares Low-Rank-Tensor-Lernen für die raumzeitliche Imputation von Verkehrsdaten . Transportation Research Teil C: Emerging Technologies, 129: 103226. [Preprint] [DOI] [Daten] [Python-Code]

• Xinyu Chen, Lijun Sun (2020). Autoregressive Tensorvervollständigung mit niedrigem Rang für multivariate Zeitreihenvorhersagen . arXiv-Vorabdruck arXiv: 2006.10436. [Vorabdruck] [Daten & Python-Code]

• Xinyu Chen, Jinming Yang, Lijun Sun (2020). „Ein nichtkonvexes Tensor-Vervollständigungsmodell mit niedrigem Rang für die raumzeitliche Verkehrsdatenimputation“ . Transportation Research Teil C: Emerging Technologies, 117: 102673. [Preprint] [DOI] [Daten & Python-Code]

• Xinyu Chen, Zhaocheng He, Yixian Chen, Yuhuan Lu, Jiawei Wang (2019). Imputation fehlender Verkehrsdaten und Mustererkennung mit einem Bayes'schen erweiterten Tensorfaktorisierungsmodell . Transportforschung Teil C: Emerging Technologies, 104: 66-77. [DOI] [Folien] [Daten] [Matlab-Code] [Python-Code]

• Xinyu Chen, Zhaocheng He, Lijun Sun (2019). „Ein Bayes’scher Tensorzerlegungsansatz für die Imputation raumzeitlicher Verkehrsdaten“ . Transportforschung Teil C: Emerging Technologies, 98: 73-84. [Vordruck] [DOI] [Daten] [Matlab-Code] [Python-Code]