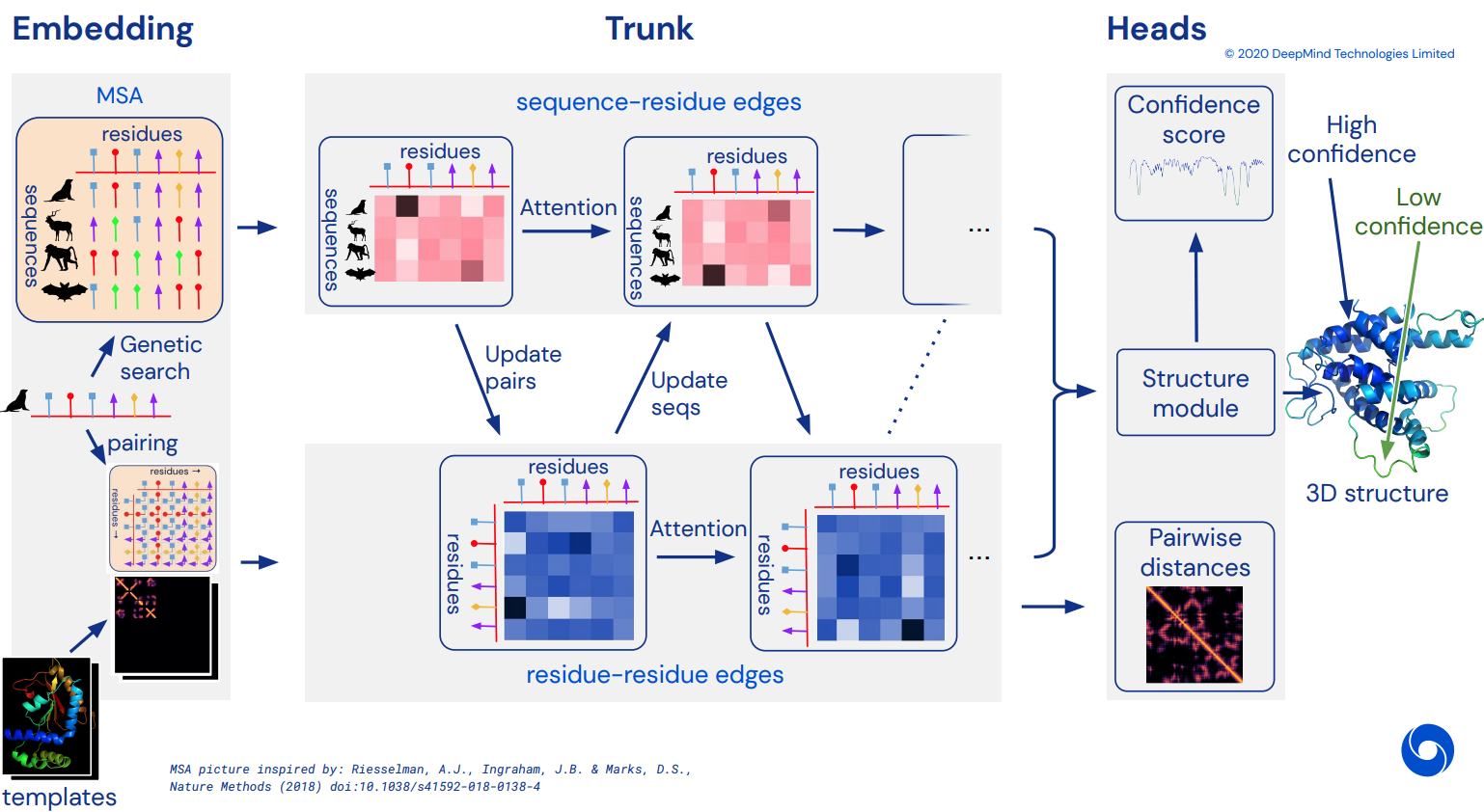
Um schließlich eine inoffizielle funktionierende Pytorch-Implementierung von Alphafold2 zu werden, dem atemberaubenden Aufmerksamkeitsnetzwerk, das CASP14 gelöst hat. Wird schrittweise implementiert, sobald weitere Details der Architektur veröffentlicht werden.
Sobald dies repliziert ist, beabsichtige ich, alle verfügbaren Aminosäuresequenzen in-silico zu falten und sie als akademischen Strom zur Förderung der Wissenschaft freizugeben. Wenn Sie an Replikationsbemühungen interessiert sind, schauen Sie bitte bei #alphafold auf diesem Discord-Kanal vorbei
Update: Deepmind hat den offiziellen Code in Jax zusammen mit den Gewichten als Open Source bereitgestellt! Dieses Repository wird nun auf eine reine Pytorch-Übersetzung mit einigen Verbesserungen bei der Positionskodierung ausgerichtet sein
ArxivInsights-Video
$ pip install alphafold2-pytorchlhatsk hat berichtet, dass ein modifizierter Trunk dieses Repositorys mit demselben Setup wie trRosetta trainiert wurde, mit konkurrenzfähigen Ergebnissen
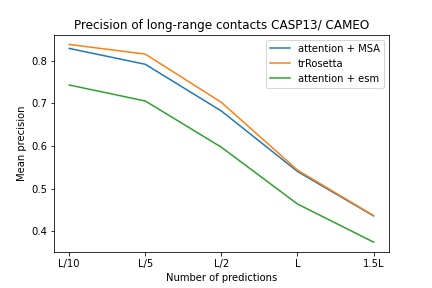
blue used the the trRosetta input (MSA -> potts -> axial attention), green used the ESM embedding (only sequence) -> tiling -> axial attention - lhatsk
Vorhersage des Distogramms, wie Alphafold-1, aber mit Aufmerksamkeit
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
reversible = False # set this to True for fully reversible self / cross attention for the trunk
). cuda ()
seq = torch . randint ( 0 , 21 , ( 1 , 128 )). cuda () # AA length of 128
msa = torch . randint ( 0 , 21 , ( 1 , 5 , 120 )). cuda () # MSA doesn't have to be the same length as primary sequence
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
distogram = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) # (1, 128, 128, 37) Sie können die Vorhersage für die Winkel auch aktivieren, indem Sie predict_angles = True bei init übergeben. Das folgende Beispiel wäre äquivalent zu trRosetta, jedoch mit Selbst-/Queraufmerksamkeit.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
predict_angles = True # set this to True
). cuda ()
seq = torch . randint ( 0 , 21 , ( 1 , 128 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 1 , 5 , 120 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
distogram , theta , phi , omega = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
)
# distogram - (1, 128, 128, 37),
# theta - (1, 128, 128, 25),
# phi - (1, 128, 128, 13),
# omega - (1, 128, 128, 25) In Fabians aktuellem Aufsatz wird vorgeschlagen, dass die iterative Rückführung der Koordinaten in den SE3 Transformer mit geteilter Gewichtung funktionieren könnte. Ich habe beschlossen, diese Idee umzusetzen, auch wenn noch unklar ist, wie sie tatsächlich funktioniert.
Sie können zur Strukturverfeinerung auch E(n)-Transformer oder EGNN verwenden.
Update: Bakers Labor hat gezeigt, dass eine End-to-End-Architektur von Sequenz- und MSA-Einbettungen bis hin zu SE3-Transformern trRosetta am besten kann und die Lücke zu Alphafold2 schließt. Wir werden den Graph Transformer verwenden, der auf die Stammeinbettungen einwirkt, um den anfänglichen Koordinatensatz zu generieren, der an das äquivariante Netzwerk gesendet wird. (Dies wird von Costa et al. in ihrer Arbeit weiter bestätigt, in der sie 3D-Koordinaten aus MSA Transformer-Einbettungen in einem Aufsatz aus der Zeit vor dem Baker-Labor ermittelten.)
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
predict_coords = True ,
structure_module_type = 'se3' , # use SE3 Transformer - if set to False, will use E(n)-Transformer, Victor and Max Welling's new paper
structure_module_dim = 4 , # se3 transformer dimension
structure_module_depth = 1 , # depth
structure_module_heads = 1 , # heads
structure_module_dim_head = 16 , # dimension of heads
structure_module_refinement_iters = 2 , # number of equivariant coordinate refinement iterations
structure_num_global_nodes = 1 # number of global nodes for the structure module, only works with SE3 transformer
). cuda ()
seq = torch . randint ( 0 , 21 , ( 2 , 64 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 2 , 5 , 60 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
coords = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) # (2, 64 * 3, 3) <-- 3 atoms per residue Die zugrunde liegende Annahme ist, dass der Stamm auf der Restebene arbeitet und dann die atomare Ebene für das Strukturmodul darstellt, unabhängig davon, ob es sich um SE3-Transformer, E(n)-Transformer oder EGNN handelt, die die Verfeinerung durchführen. Diese Bibliothek enthält standardmäßig die drei Grundgerüstatome (C, Ca, N), aber Sie können sie so konfigurieren, dass sie jedes andere Atom Ihrer Wahl enthält, einschließlich Cb und der Seitenketten.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
predict_coords = True ,
atoms = 'backbone-with-cbeta'
). cuda ()
seq = torch . randint ( 0 , 21 , ( 2 , 64 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 2 , 5 , 60 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
coords = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) # (2, 64 * 4, 3) <-- 4 atoms per residue (C, Ca, N, Cb) Zu den gültigen Optionen für atoms gehören:
backbone – 3 Rückgratatome (C, Ca, N) [Standard]backbone-with-cbeta – 3 Rückgratatome und C Betabackbone-with-oxygen – 3 Rückgratatome und Sauerstoff aus Carboxylbackbone-with-cbeta-and-oxygen – 3 Rückgratatome mit C-Beta und Sauerstoffall – Rückgrat und alle anderen Atome aus der SeitenketteSie können auch einen Tensor der Form (14,) übergeben, der definiert, welche Atome Sie einbeziehen möchten
ex.
atoms = torch . tensor ([ 1 , 1 , 1 , 1 , 1 , 1 , 0 , 1 , 0 , 0 , 0 , 0 , 0 , 1 ])Dieses Repository bietet Ihnen eine einfache Ergänzung des Netzwerks mit vorab trainierten Einbettungen von Facebook AI. Es enthält Wrapper für die vorab trainierten ESM-, MSA-Transformer oder Protein-Transformer.
Es gibt einige Voraussetzungen. Sie müssen sicherstellen, dass Sie die Apex-Bibliothek von Nvidia installiert haben, da die vorab trainierten Transformatoren einige Fusionsoperationen verwenden.
Oder Sie können versuchen, das folgende Skript auszuführen
git clone https://github.com/NVIDIA/apex
cd apex
pip install -v --disable-pip-version-check --no-cache-dir --global-option= " --cpp_ext " --global-option= " --cuda_ext " ./ Als Nächstes müssen Sie lediglich Ihre Alphafold2 -Instanz importieren und mit einem ESMEmbedWrapper , MSAEmbedWrapper oder ProtTranEmbedWrapper umschließen. Dieser kümmert sich dann um die Einbettung sowohl der Sequenz als auch der Ausrichtungen mehrerer Sequenzen für Sie (und projiziert sie auf die auf Ihrer Website angegebenen Dimensionen). Modell). Außer dem Hinzufügen des Wrappers muss nichts geändert werden.
import torch
from alphafold2_pytorch import Alphafold2
from alphafold2_pytorch . embeds import MSAEmbedWrapper
alphafold2 = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64
)
model = MSAEmbedWrapper (
alphafold2 = alphafold2
). cuda ()
seq = torch . randint ( 0 , 21 , ( 2 , 16 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa = torch . randint ( 0 , 21 , ( 2 , 5 , 16 )). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
distogram = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) Selbst wenn der Wrapper den Trunk mit der Sequenz und den MSA-Einbettungen versorgt, werden diese standardmäßig mit den üblichen Token-Einbettungen summiert. Wenn Sie Alphafold2 ohne Token-Einbettungen trainieren möchten (verlassen Sie sich nur auf vorab trainierte Einbettungen), müssen Sie disable_token_embed bei Alphafold2 Initialisierung auf True setzen.
alphafold2 = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
disable_token_embed = True
) In einem Aufsatz von Jinbo Sie können dies nutzen, indem Sie ein Flag predict_real_value_distances aktivieren. In diesem Fall hat die zurückgegebene Distanzvorhersage eine Dimension von 2 für den Mittelwert bzw. die Standardabweichung.
Wenn predict_coords ebenfalls aktiviert ist, akzeptiert der MDS die Mittelwert- und Standardabweichungsvorhersagen direkt, ohne dass diese aus den Distogramm-Bins berechnet werden müssen.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
predict_coords = True ,
predict_real_value_distances = True , # set this to True
structure_module_type = 'se3' ,
structure_module_dim = 4 ,
structure_module_depth = 1 ,
structure_module_heads = 1 ,
structure_module_dim_head = 16 ,
structure_module_refinement_iters = 2
). cuda ()
seq = torch . randint ( 0 , 21 , ( 2 , 64 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 2 , 5 , 60 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
coords = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) # (2, 64 * 3, 3) <-- 3 atoms per residue Sie können Faltungsblöcke sowohl für die Primärsequenz als auch für die MSA hinzufügen, indem Sie einfach ein zusätzliches Schlüsselwortargument use_conv = True festlegen
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
use_conv = True # set this to True
). cuda ()
seq = torch . randint ( 0 , 21 , ( 1 , 128 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 1 , 5 , 120 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
distogram = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) # (1, 128, 128, 37)Die Faltungskerne folgen dem Beispiel dieses Artikels und kombinieren 1D- und 2D-Kernel in einem Resnet-ähnlichen Block. Sie können die Kernel als solche vollständig anpassen.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
use_conv = True , # set this to True
conv_seq_kernels = (( 9 , 1 ), ( 1 , 9 ), ( 3 , 3 )), # kernels for N x N primary sequence
conv_msa_kernels = (( 1 , 9 ), ( 3 , 3 )), # kernels for {num MSAs} x N MSAs
). cuda ()
seq = torch . randint ( 0 , 21 , ( 1 , 128 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 1 , 5 , 120 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
distogram = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) # (1, 128, 128, 37) Sie können die Zykluserweiterung auch mit einem zusätzlichen Schlüsselwortargument durchführen. Die Standarddilatation ist 1 für alle Ebenen.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
use_conv = True , # set this to True
dilations = ( 1 , 3 , 5 ) # cycle between dilations of 1, 3, 5
). cuda ()
seq = torch . randint ( 0 , 21 , ( 1 , 128 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 1 , 5 , 120 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
distogram = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) # (1, 128, 128, 37) Anstatt schließlich dem Muster aus Windungen, Selbstaufmerksamkeit und Queraufmerksamkeit pro Tiefenwiederholung zu folgen, können Sie mit dem Schlüsselwort custom_block_types jede gewünschte Reihenfolge anpassen
ex. Ein Netzwerk, in dem Sie hauptsächlich Faltungen zuerst durchführen, gefolgt von Selbstaufmerksamkeits- und Kreuzaufmerksamkeitsblöcken
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
heads = 8 ,
dim_head = 64 ,
custom_block_types = (
* (( 'conv' ,) * 6 ),
* (( 'self' , 'cross' ) * 6 )
)
). cuda ()
seq = torch . randint ( 0 , 21 , ( 1 , 128 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 1 , 5 , 120 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
distogram = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) # (1, 128, 128, 37) Sie können mit Sparse Attention von Microsoft Deepspeed trainieren, müssen jedoch den Installationsprozess über sich ergehen lassen. Es ist zweistufig.
Zuerst müssen Sie Deepspeed mit Sparse Attention installieren
$ sh install_deepspeed.sh Als nächstes müssen Sie das Pip-Paket triton installieren
$ pip install tritonWenn beide oben genannten Schritte erfolgreich waren, können Sie jetzt mit Sparse Attention trainieren!
Leider dient die spärliche Aufmerksamkeit nur der Selbstaufmerksamkeit und nicht der Queraufmerksamkeit. Ich werde eine andere Lösung einbringen, um die Kreuzaufmerksamkeit leistungsfähig zu machen.
model = Alphafold2 (
dim = 256 ,
depth = 12 ,
heads = 8 ,
dim_head = 64 ,
max_seq_len = 2048 , # the maximum sequence length, this is required for sparse attention. the input cannot exceed what is set here
sparse_self_attn = ( True , False ) * 6 # interleave sparse and full attention for all 12 layers
). cuda ()Ich habe auch eine der besten linearen Aufmerksamkeitsvarianten hinzugefügt, in der Hoffnung, die Belastung durch gegenseitige Aufmerksamkeit zu verringern. Ich persönlich finde, dass Performer nicht so gut funktioniert, aber da in der Arbeit einige gute Zahlen für Protein-Benchmarks angegeben wurden, dachte ich, ich würde es einbeziehen und anderen das Experimentieren ermöglichen.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
cross_attn_linear = True # simply set this to True to use Performer for all cross attention
). cuda ()Sie können auch die genauen Ebenen angeben, für die Sie lineare Aufmerksamkeit verwenden möchten, indem Sie ein Tupel mit der gleichen Länge wie die Tiefe übergeben
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 6 ,
heads = 8 ,
dim_head = 64 ,
cross_attn_linear = ( True , False ) * 3 # interleave linear and full attention
). cuda ()Dieser Artikel schlägt vor, dass Sie bei Abfragen oder Kontexten, die über definierte Achsen verfügen (z. B. ein Bild), die erforderliche Aufmerksamkeit reduzieren können, indem Sie über diese Achsen (Höhe und Breite) mitteln und die gemittelten Achsen in einer Sequenz verketten. Sie können dies als speichersparende Technik für die Queraufmerksamkeit aktivieren, insbesondere für die Primärsequenz.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 6 ,
heads = 8 ,
dim_head = 64 ,
cross_attn_kron_primary = True # make sure primary sequence undergoes the kronecker operator during cross attention
). cuda () Sie können den gleichen Operator auch während der Queraufmerksamkeit mit dem Flag cross_attn_kron_msa auf die MSAs anwenden, wenn Ihre MSAs ausgerichtet sind und die gleiche Breite haben.
Todo
Um Speicherplatz für unerwünschte Aufmerksamkeit zu sparen, können Sie ein Komprimierungsverhältnis für die Schlüssel/Werte festlegen, indem Sie dem in diesem Dokument beschriebenen Schema folgen. Ein Komprimierungsverhältnis von 2–4 ist normalerweise akzeptabel.
model = Alphafold2 (
dim = 256 ,
depth = 12 ,
heads = 8 ,
dim_head = 64 ,
cross_attn_compress_ratio = 3
). cuda ()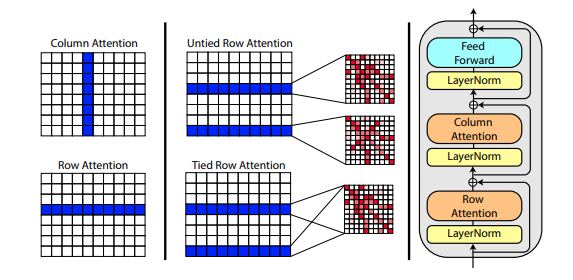
In einem neuen Artikel von Roshan Rao wird vorgeschlagen, die axiale Aufmerksamkeit für das Vortraining auf MSAs zu nutzen. Angesichts der starken Ergebnisse wird dieses Repository dasselbe Schema im Trunk verwenden, insbesondere für die MSA-Selbstaufmerksamkeit.
Sie können die Zeilenaufmerksamkeiten des MSA auch mit der Einstellung msa_tie_row_attn = True bei der Initialisierung von Alphafold2 verknüpfen. Um dies nutzen zu können, müssen Sie jedoch sicherstellen, dass bei einer ungeraden Anzahl von MSAs pro Primärsequenz die MSA-Maske für die nicht verwendeten Zeilen ordnungsgemäß auf False gesetzt ist.
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
msa_tie_row_attn = True # just set this to true
)Die Vorlagenverarbeitung erfolgt ebenfalls weitgehend mit axialer Aufmerksamkeit, wobei die Queraufmerksamkeit entlang der Dimension „Anzahl der Vorlagen“ erfolgt. Dies folgt im Großen und Ganzen dem gleichen Schema wie der hier gezeigte aktuelle All-Attention-Ansatz zur Videoklassifizierung.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 5 ,
heads = 8 ,
dim_head = 64 ,
reversible = True ,
sparse_self_attn = False ,
max_seq_len = 256 ,
cross_attn_compress_ratio = 3
). cuda ()
seq = torch . randint ( 0 , 21 , ( 1 , 16 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa = torch . randint ( 0 , 21 , ( 1 , 10 , 16 )). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
templates_seq = torch . randint ( 0 , 21 , ( 1 , 2 , 16 )). cuda ()
templates_coors = torch . randint ( 0 , 37 , ( 1 , 2 , 16 , 3 )). cuda ()
templates_mask = torch . ones_like ( templates_seq ). bool (). cuda ()
distogram = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask ,
templates_seq = templates_seq ,
templates_coors = templates_coors ,
templates_mask = templates_mask
)Wenn auch Seitenketteninformationen in Form des Einheitsvektors zwischen den C- und C-Alpha-Koordinaten jedes Rests vorhanden sind, können Sie diese auch wie folgt übergeben.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 5 ,
heads = 8 ,
dim_head = 64 ,
reversible = True ,
sparse_self_attn = False ,
max_seq_len = 256 ,
cross_attn_compress_ratio = 3
). cuda ()
seq = torch . randint ( 0 , 21 , ( 1 , 16 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa = torch . randint ( 0 , 21 , ( 1 , 10 , 16 )). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
templates_seq = torch . randint ( 0 , 21 , ( 1 , 2 , 16 )). cuda ()
templates_coors = torch . randn ( 1 , 2 , 16 , 3 ). cuda ()
templates_mask = torch . ones_like ( templates_seq ). bool (). cuda ()
templates_sidechains = torch . randn ( 1 , 2 , 16 , 3 ). cuda () # unit vectors of difference of C and C-alpha coordinates
distogram = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask ,
templates_seq = templates_seq ,
templates_mask = templates_mask ,
templates_coors = templates_coors ,
templates_sidechains = templates_sidechains
)Ich habe eine Neuimplementierung von SE3 Transformer vorbereitet, wie Fabian Fuchs in einem spekulativen Blogbeitrag erklärt.
Darüber hinaus verwendet ein neues Papier von Victor und Welling invariante Merkmale für die E(n)-Äquivarianz, erreicht SOTA und übertrifft SE3 Transformer bei einer Reihe von Benchmarks, während es gleichzeitig viel schneller ist. Ich habe die Hauptideen dieses Dokuments übernommen und es in einen Transformator umgewandelt (wobei sowohl den Funktionen Aufmerksamkeit geschenkt als auch Aktualisierungen koordiniert wurden).
Alle drei oben genannten äquivarianten Netzwerke wurden integriert und können im Repository zur Verfeinerung atomarer Koordinaten verwendet werden, indem einfach ein Hyperparameter structure_module_type festgelegt wird.
se3 SE3 Transformator
egnn EGNN
en E(n)-Transformer
Interessant für die Leser ist, dass jedes der drei Frameworks auch von Forschern zu verwandten Problemen validiert wurde.
$ python setup.py test Diese Bibliothek wird die großartige Arbeit von Jonathan King in diesem Repository nutzen. Danke Jonathan!
Wir haben auch die MSA-Daten im Wert von ca. 3,5 TB, die von Archivar, dem Eigentümer des The-Eye-Projekts, heruntergeladen und gehostet wurden. (Sie hosten auch die Daten und Modelle für Eleuther AI.) Bitte erwägen Sie eine Spende, wenn Sie sie hilfreich finden.
$ curl -s https://the-eye.eu/eleuther_staging/globus_stuffs/tree.txthttps://xukui.cn/alphafold2.html
https://moalquraishi.wordpress.com/2020/12/08/alphafold2-casp14-it-feels-like-ones-child-has-left-home/

https://www.biorxiv.org/content/10.1101/2020.12.10.419994v1.full.pdf
https://pubmed.ncbi.nlm.nih.gov/33637700/
tFold-Präsentation von Tencent AI Labs
cd downloads_folder > pip install pyrosetta_wheel_filename.whlOpenMM Amber
@misc { unpublished2021alphafold2 ,
title = { Alphafold2 } ,
author = { John Jumper } ,
year = { 2020 } ,
archivePrefix = { arXiv } ,
primaryClass = { q-bio.BM }
} @article { Rao2021.02.12.430858 ,
author = { Rao, Roshan and Liu, Jason and Verkuil, Robert and Meier, Joshua and Canny, John F. and Abbeel, Pieter and Sercu, Tom and Rives, Alexander } ,
title = { MSA Transformer } ,
year = { 2021 } ,
publisher = { Cold Spring Harbor Laboratory } ,
URL = { https://www.biorxiv.org/content/early/2021/02/13/2021.02.12.430858 } ,
journal = { bioRxiv }
} @article { Rives622803 ,
author = { Rives, Alexander and Goyal, Siddharth and Meier, Joshua and Guo, Demi and Ott, Myle and Zitnick, C. Lawrence and Ma, Jerry and Fergus, Rob } ,
title = { Biological Structure and Function Emerge from Scaling Unsupervised Learning to 250 Million Protein Sequences } ,
year = { 2019 } ,
doi = { 10.1101/622803 } ,
publisher = { Cold Spring Harbor Laboratory } ,
journal = { bioRxiv }
} @article { Elnaggar2020.07.12.199554 ,
author = { Elnaggar, Ahmed and Heinzinger, Michael and Dallago, Christian and Rehawi, Ghalia and Wang, Yu and Jones, Llion and Gibbs, Tom and Feher, Tamas and Angerer, Christoph and Steinegger, Martin and BHOWMIK, DEBSINDHU and Rost, Burkhard } ,
title = { ProtTrans: Towards Cracking the Language of Life{textquoteright}s Code Through Self-Supervised Deep Learning and High Performance Computing } ,
elocation-id = { 2020.07.12.199554 } ,
year = { 2021 } ,
doi = { 10.1101/2020.07.12.199554 } ,
publisher = { Cold Spring Harbor Laboratory } ,
URL = { https://www.biorxiv.org/content/early/2021/05/04/2020.07.12.199554 } ,
eprint = { https://www.biorxiv.org/content/early/2021/05/04/2020.07.12.199554.full.pdf } ,
journal = { bioRxiv }
} @misc { king2020sidechainnet ,
title = { SidechainNet: An All-Atom Protein Structure Dataset for Machine Learning } ,
author = { Jonathan E. King and David Ryan Koes } ,
year = { 2020 } ,
eprint = { 2010.08162 } ,
archivePrefix = { arXiv } ,
primaryClass = { q-bio.BM }
} @misc { alquraishi2019proteinnet ,
title = { ProteinNet: a standardized data set for machine learning of protein structure } ,
author = { Mohammed AlQuraishi } ,
year = { 2019 } ,
eprint = { 1902.00249 } ,
archivePrefix = { arXiv } ,
primaryClass = { q-bio.BM }
} @misc { gomez2017reversible ,
title = { The Reversible Residual Network: Backpropagation Without Storing Activations } ,
author = { Aidan N. Gomez and Mengye Ren and Raquel Urtasun and Roger B. Grosse } ,
year = { 2017 } ,
eprint = { 1707.04585 } ,
archivePrefix = { arXiv } ,
primaryClass = { cs.CV }
} @misc { fuchs2021iterative ,
title = { Iterative SE(3)-Transformers } ,
author = { Fabian B. Fuchs and Edward Wagstaff and Justas Dauparas and Ingmar Posner } ,
year = { 2021 } ,
eprint = { 2102.13419 } ,
archivePrefix = { arXiv } ,
primaryClass = { cs.LG }
} @misc { satorras2021en ,
title = { E(n) Equivariant Graph Neural Networks } ,
author = { Victor Garcia Satorras and Emiel Hoogeboom and Max Welling } ,
year = { 2021 } ,
eprint = { 2102.09844 } ,
archivePrefix = { arXiv } ,
primaryClass = { cs.LG }
} @misc { su2021roformer ,
title = { RoFormer: Enhanced Transformer with Rotary Position Embedding } ,
author = { Jianlin Su and Yu Lu and Shengfeng Pan and Bo Wen and Yunfeng Liu } ,
year = { 2021 } ,
eprint = { 2104.09864 } ,
archivePrefix = { arXiv } ,
primaryClass = { cs.CL }
} @article { Gao_2020 ,
title = { Kronecker Attention Networks } ,
ISBN = { 9781450379984 } ,
url = { http://dx.doi.org/10.1145/3394486.3403065 } ,
DOI = { 10.1145/3394486.3403065 } ,
journal = { Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining } ,
publisher = { ACM } ,
author = { Gao, Hongyang and Wang, Zhengyang and Ji, Shuiwang } ,
year = { 2020 } ,
month = { Jul }
} @article { Si2021.05.10.443415 ,
author = { Si, Yunda and Yan, Chengfei } ,
title = { Improved protein contact prediction using dimensional hybrid residual networks and singularity enhanced loss function } ,
elocation-id = { 2021.05.10.443415 } ,
year = { 2021 } ,
doi = { 10.1101/2021.05.10.443415 } ,
publisher = { Cold Spring Harbor Laboratory } ,
URL = { https://www.biorxiv.org/content/early/2021/05/11/2021.05.10.443415 } ,
eprint = { https://www.biorxiv.org/content/early/2021/05/11/2021.05.10.443415.full.pdf } ,
journal = { bioRxiv }
} @article { Costa2021.06.02.446809 ,
author = { Costa, Allan and Ponnapati, Manvitha and Jacobson, Joseph M. and Chatterjee, Pranam } ,
title = { Distillation of MSA Embeddings to Folded Protein Structures with Graph Transformers } ,
year = { 2021 } ,
doi = { 10.1101/2021.06.02.446809 } ,
publisher = { Cold Spring Harbor Laboratory } ,
URL = { https://www.biorxiv.org/content/early/2021/06/02/2021.06.02.446809 } ,
eprint = { https://www.biorxiv.org/content/early/2021/06/02/2021.06.02.446809.full.pdf } ,
journal = { bioRxiv }
} @article { Baek2021.06.14.448402 ,
author = { Baek, Minkyung and DiMaio, Frank and Anishchenko, Ivan and Dauparas, Justas and Ovchinnikov, Sergey and Lee, Gyu Rie and Wang, Jue and Cong, Qian and Kinch, Lisa N. and Schaeffer, R. Dustin and Mill{'a}n, Claudia and Park, Hahnbeom and Adams, Carson and Glassman, Caleb R. and DeGiovanni, Andy and Pereira, Jose H. and Rodrigues, Andria V. and van Dijk, Alberdina A. and Ebrecht, Ana C. and Opperman, Diederik J. and Sagmeister, Theo and Buhlheller, Christoph and Pavkov-Keller, Tea and Rathinaswamy, Manoj K and Dalwadi, Udit and Yip, Calvin K and Burke, John E and Garcia, K. Christopher and Grishin, Nick V. and Adams, Paul D. and Read, Randy J. and Baker, David } ,
title = { Accurate prediction of protein structures and interactions using a 3-track network } ,
year = { 2021 } ,
doi = { 10.1101/2021.06.14.448402 } ,
publisher = { Cold Spring Harbor Laboratory } ,
URL = { https://www.biorxiv.org/content/early/2021/06/15/2021.06.14.448402 } ,
eprint = { https://www.biorxiv.org/content/early/2021/06/15/2021.06.14.448402.full.pdf } ,
journal = { bioRxiv }
}