@article{chen2020neurodiffeq,
title={NeuroDiffEq: A Python package for solving differential equations with neural networks},
author={Chen, Feiyu and Sondak, David and Protopapas, Pavlos and Mattheakis, Marios and Liu, Shuheng and Agarwal, Devansh and Di Giovanni, Marco},
journal={Journal of Open Source Software},
volume={5},
number={46},
pages={1931},
year={2020}
}Wussten Sie, dass neurodiffeq Lösungspakete unterstützt und zur Lösung umgekehrter Probleme verwendet werden kann? Sehen Sie hier!
? Kennen Sie schon neurodiffeq? ? Gehen Sie zu den FAQs.
neurodiffeq ist ein Paket zur Lösung von Differentialgleichungen mit neuronalen Netzen. Differentialgleichungen sind Gleichungen, die eine Funktion mit ihren Ableitungen in Beziehung setzen. Sie entstehen in verschiedenen wissenschaftlichen und technischen Bereichen. Traditionell können diese Probleme mit numerischen Methoden (z. B. Finite-Differenzen, Finite-Elemente) gelöst werden. Obwohl diese Methoden effektiv und angemessen sind, ist ihre Aussagekraft durch ihre Funktionsdarstellung begrenzt. Es wäre interessant, wenn wir Lösungen für Differentialgleichungen berechnen könnten, die stetig und differenzierbar sind.
Künstliche neuronale Netze haben als universelle Funktionsnäherungen nachweislich das Potenzial, gewöhnliche Differentialgleichungen (ODEs) und partielle Differentialgleichungen (PDEs) mit bestimmten Anfangs-/Randbedingungen zu lösen. Das Ziel von neurodiffeq besteht darin, diese bestehenden Techniken zur Verwendung von KNN zur Lösung von Differentialgleichungen so zu implementieren, dass die Software flexibel genug ist, um ein breites Spektrum benutzerdefinierter Probleme zu bearbeiten.
Wie die meisten Standardbibliotheken wird neurodiffeq auf PyPI gehostet. Um die neueste stabile Version zu installieren,
pip install -U neurodiffeq # '-U' bedeutet Update auf die neueste Version
Alternativ können Sie die Bibliothek manuell installieren, um frühzeitig Zugriff auf unsere neuen Funktionen zu erhalten. Dies ist die empfohlene Methode für Entwickler, die zur Bibliothek beitragen möchten.
Git-Klon https://github.com/NeuroDiffGym/neurodiffeq.gitcd neurodiffeq && pip install -r Anforderungen pip install . # Um Änderungen an der Bibliothek vorzunehmen, verwenden Sie `pip install -e .`pytest tests/ # Führen Sie Tests aus. Optional.
Bei Fragen helfen wir Ihnen gerne weiter. In der Zwischenzeit können Sie sich die FAQs ansehen.
Die vollständigen Tutorials und die Dokumentation von neurodiffeq finden Sie in der offiziellen Dokumentation.
Zusätzlich zu den Dokumentationen haben wir kürzlich ein kurzes Demo-Video mit Folien erstellt.
aus neurodiffeq import diffaus neurodiffeq.solvers import Solver1D, Solver2Daus neurodiffeq.conditions import IVP, DirichletBVP2Daus neurodiffeq.networks import FCNN, SinActv
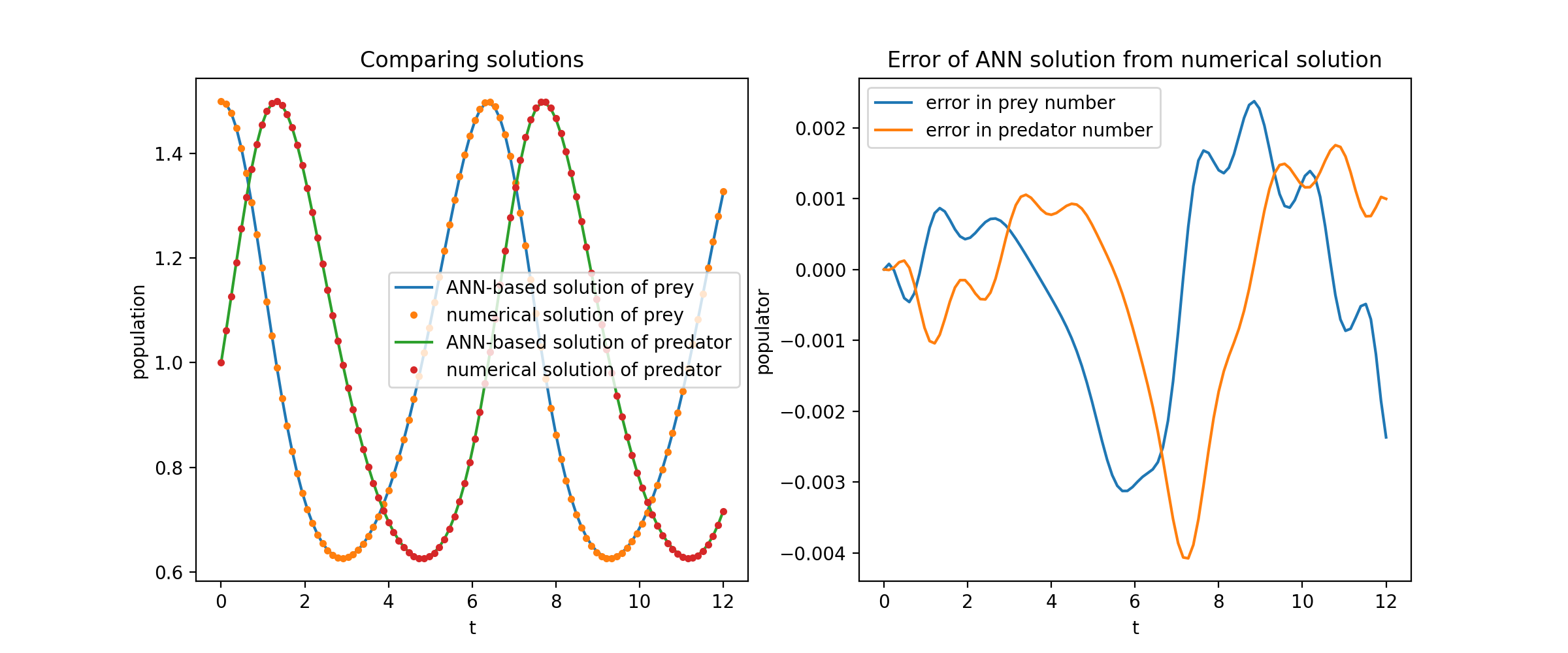
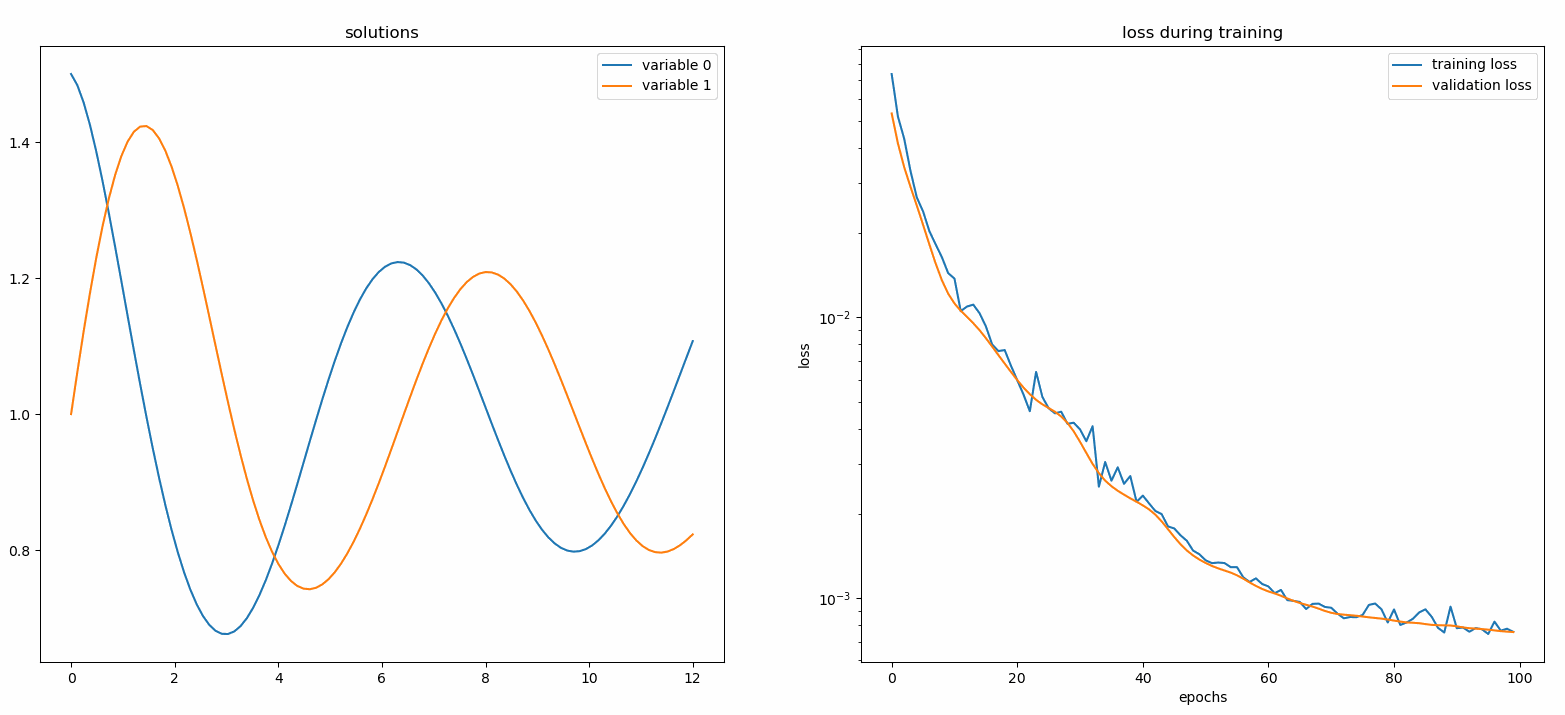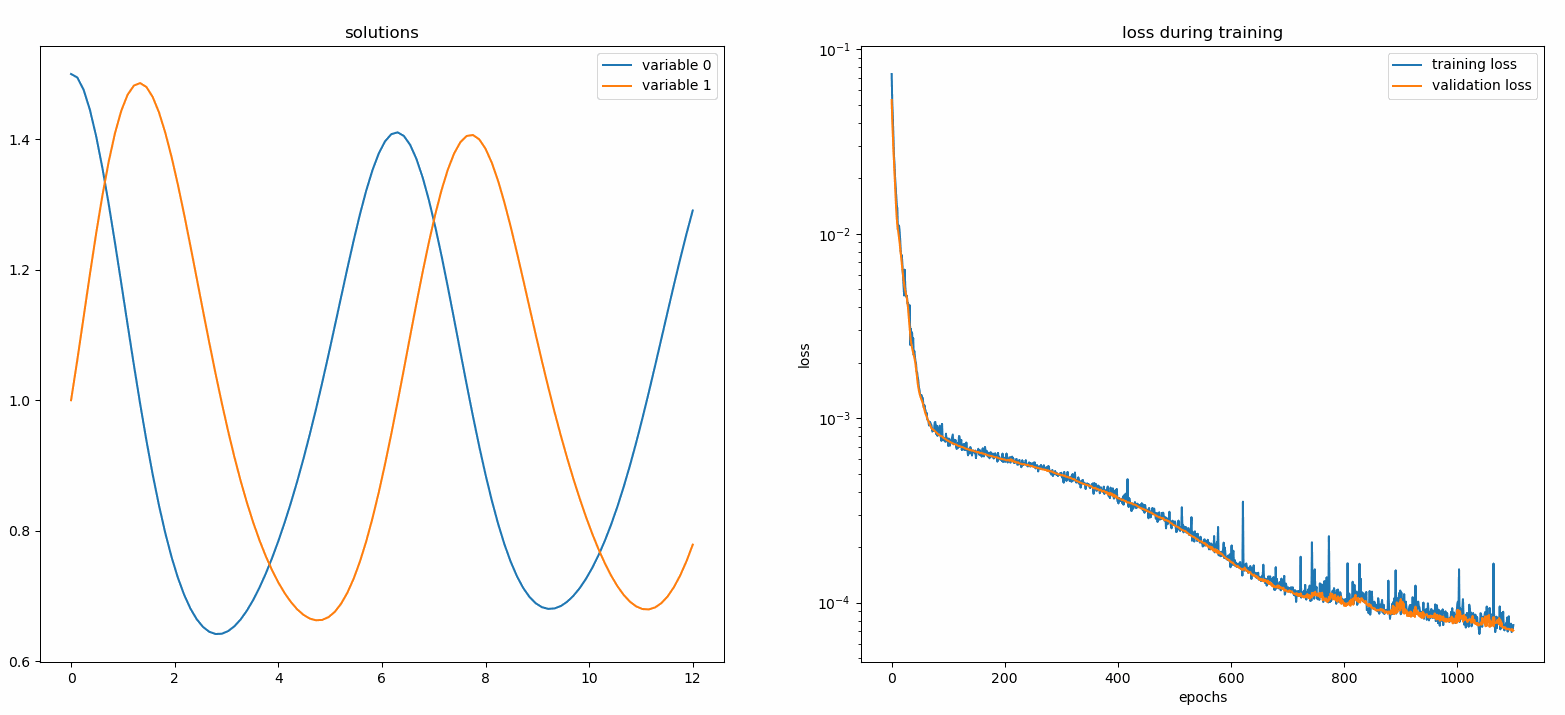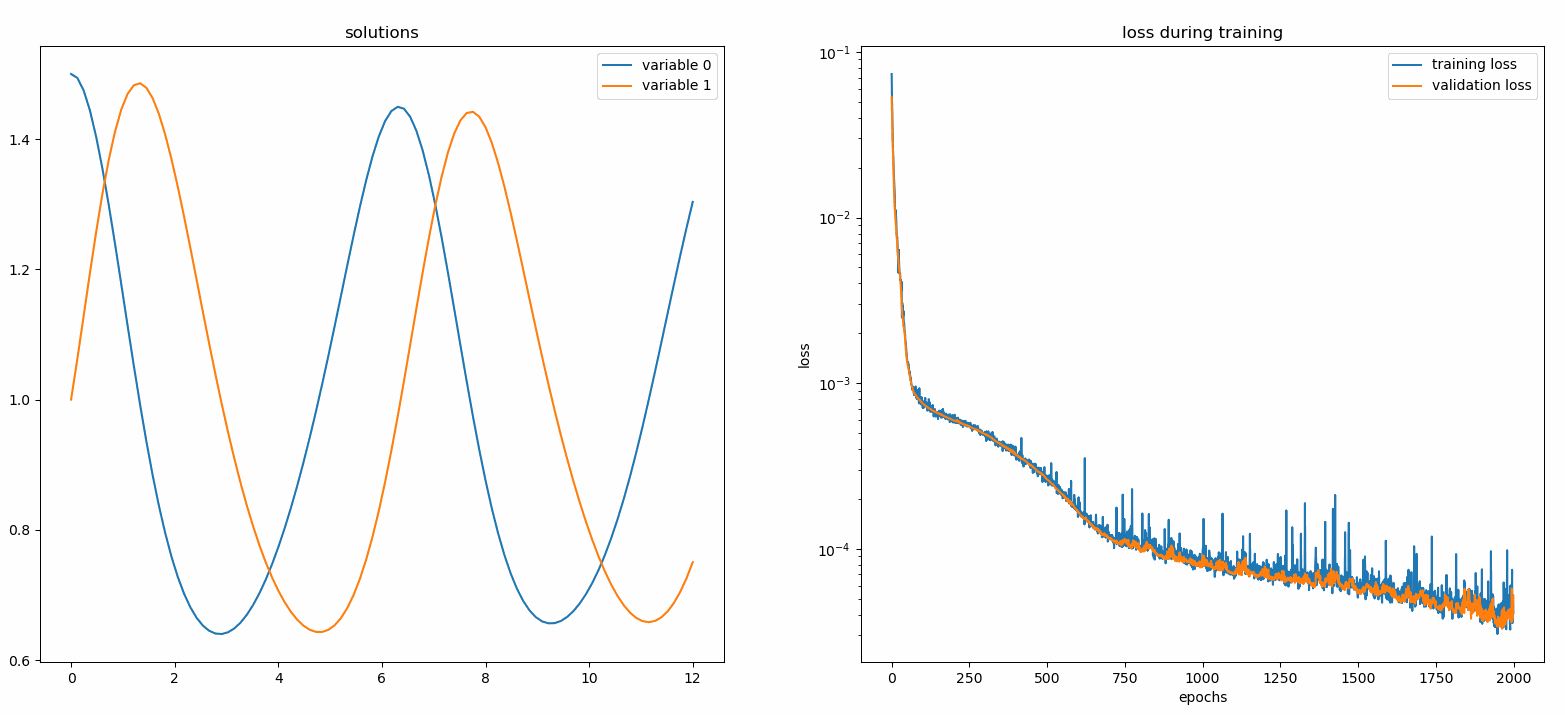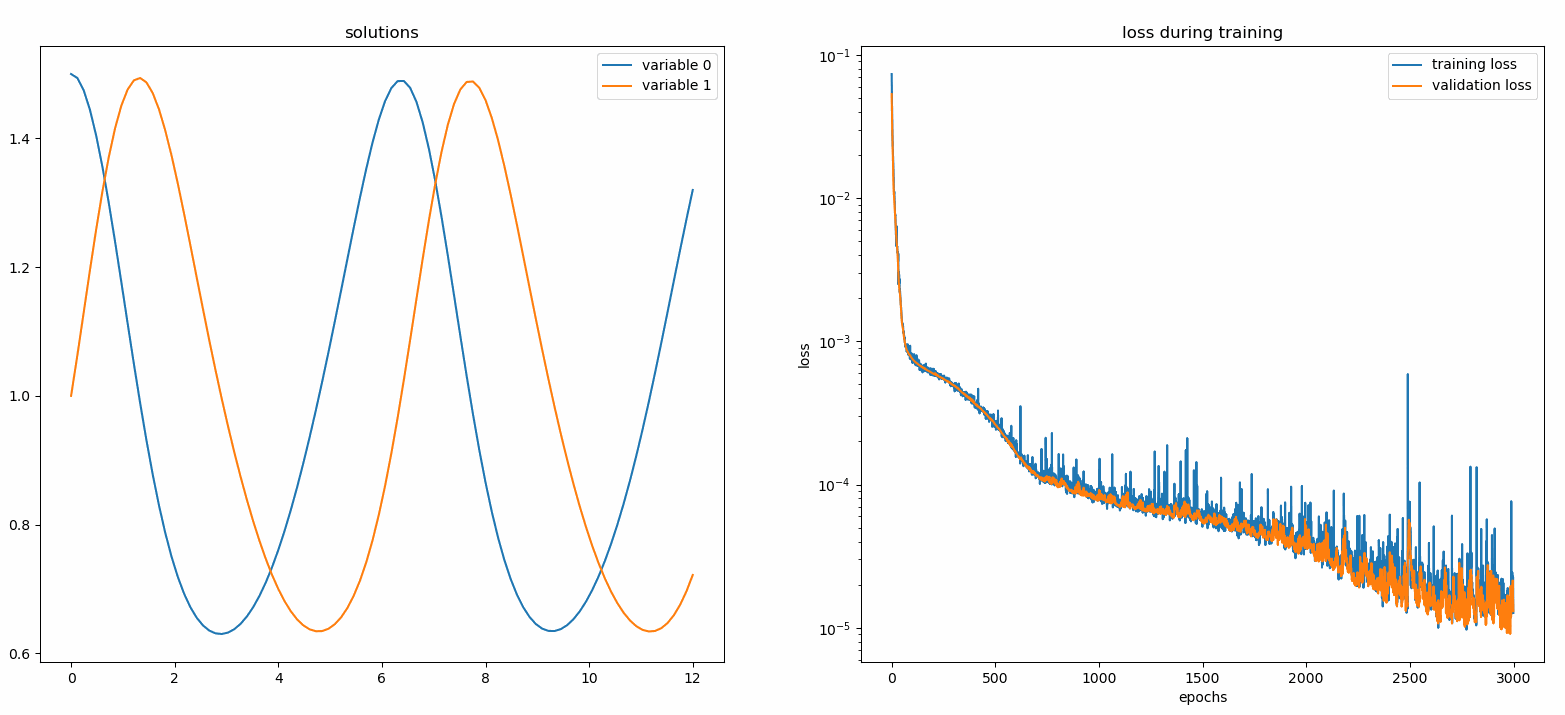
Hier lösen wir ein nichtlineares System aus zwei ODEs, bekannt als Lotka-Volterra-Gleichungen. Es gibt zwei unbekannte Funktionen ( u und v ) und eine einzelne unabhängige Variable ( t ).
def ode_system(u, v, t): return [diff(u,t)-(uu*v), diff(v,t)-(u*vv)]conditions = [IVP(t_0=0.0, u_0=1.5 ), IVP(t_0=0.0, u_0=1.0)]nets = [FCNN(actv=SinActv), FCNN(actv=SinActv)]solver = Solver1D(ode_system, Bedingungen, t_min=0,1, t_max=12,0, Netze=Netze)solver.fit(max_epochs=3000)solution =solver.get_solution()
Da solution ein aufrufbares Objekt ist, können Sie Numpy-Arrays oder Torch-Tensoren daran übergeben
u, v = Solution(t, to_numpy=True) # t kann np.ndarray oder Torch.Tensor sein
Das Auftragen u und v gegen ihre analytischen Lösungen ergibt etwa Folgendes:
Hier lösen wir eine Laplace-Gleichung mit Dirichlet-Randbedingungen auf einem Rechteck. Beachten Sie, dass wir die Laplace-Gleichung aufgrund der Einfachheit der Berechnung der analytischen Lösung gewählt haben. In der Praxis können Sie alle nichtlinearen, chaotischen PDEs ausprobieren , vorausgesetzt, Sie optimieren den Löser gut genug.
Das Lösen eines 2D-PDE-Systems ist dem Lösen von ODEs ziemlich ähnlich, außer dass es zwei Variablen x und y für Randwertprobleme oder x und t für anfängliche Randwertprobleme gibt, die beide unterstützt werden.
def pde_system(u, x, y):return [diff(u, x, order=2) + diff(u, y, order=2)]conditions = [DirichletBVP2D(x_min=0, x_min_val=lambda y: Torch. sin(np.pi*y),x_max=1, x_max_val=lambda y: 0, y_min=0, y_min_val=Lambda x: 0, y_max=1, y_max_val=Lambda x: 0,
)
]nets = [FCNN(n_input_units=2, n_output_units=1, versteckte_einheiten=(512,))]solver = Solver2D(pde_system, Bedingungen, xy_min=(0, 0), xy_max=(1, 1), nets=nets) Solver.fit(max_epochs=2000)solution = Solver.get_solution() Die solution einer 2D-PDE unterscheidet sich geringfügig von der einer ODE. Auch hier werden entweder Numpy-Arrays oder Torch-Tensoren verwendet.
u = Lösung(x, y, to_numpy=True)
Die Auswertung von u auf [0,1] × [0,1] ergibt die folgenden Diagramme
| ANN-basierte Lösung | Rest von PDE |
|---|---|
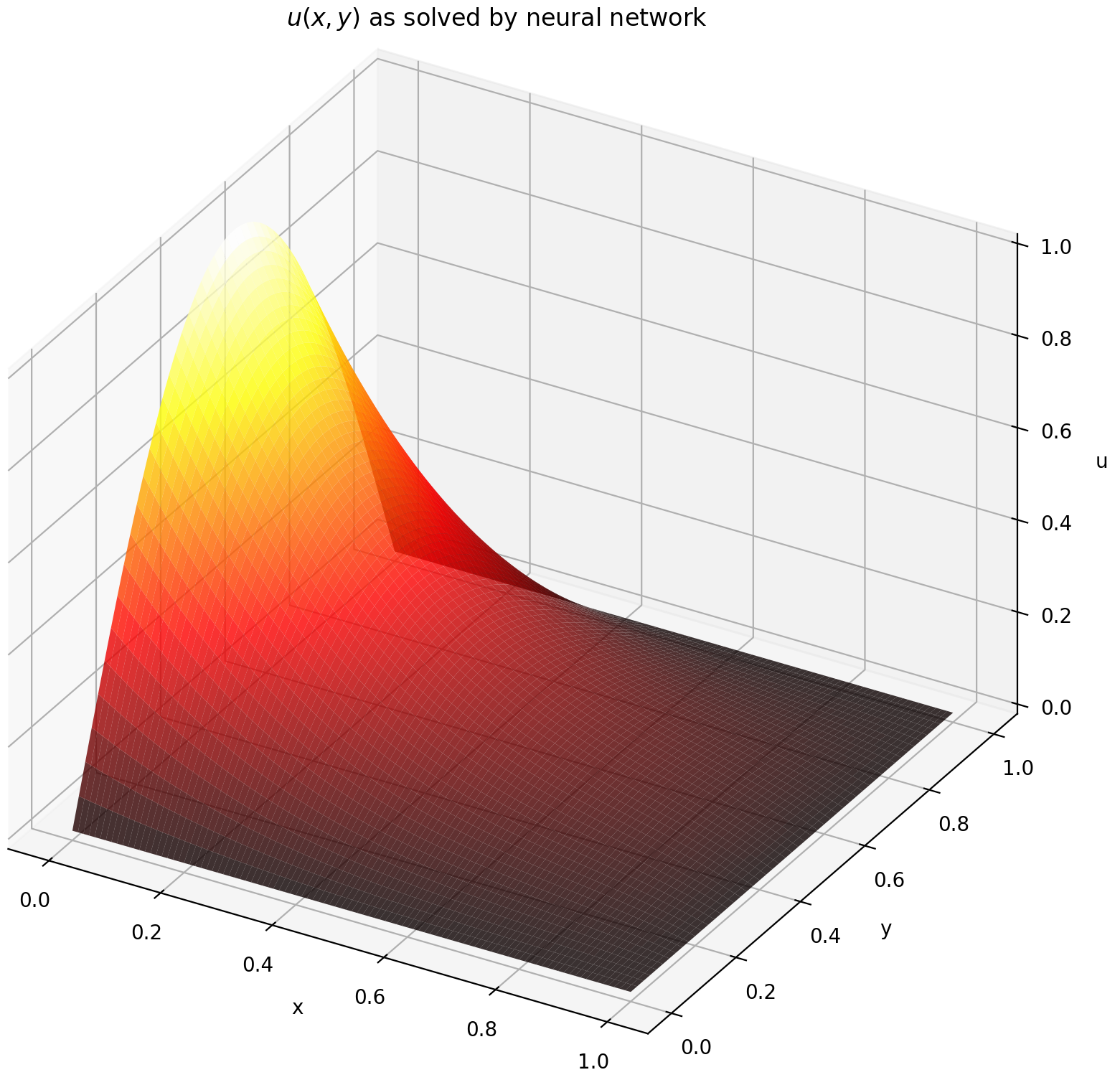 | 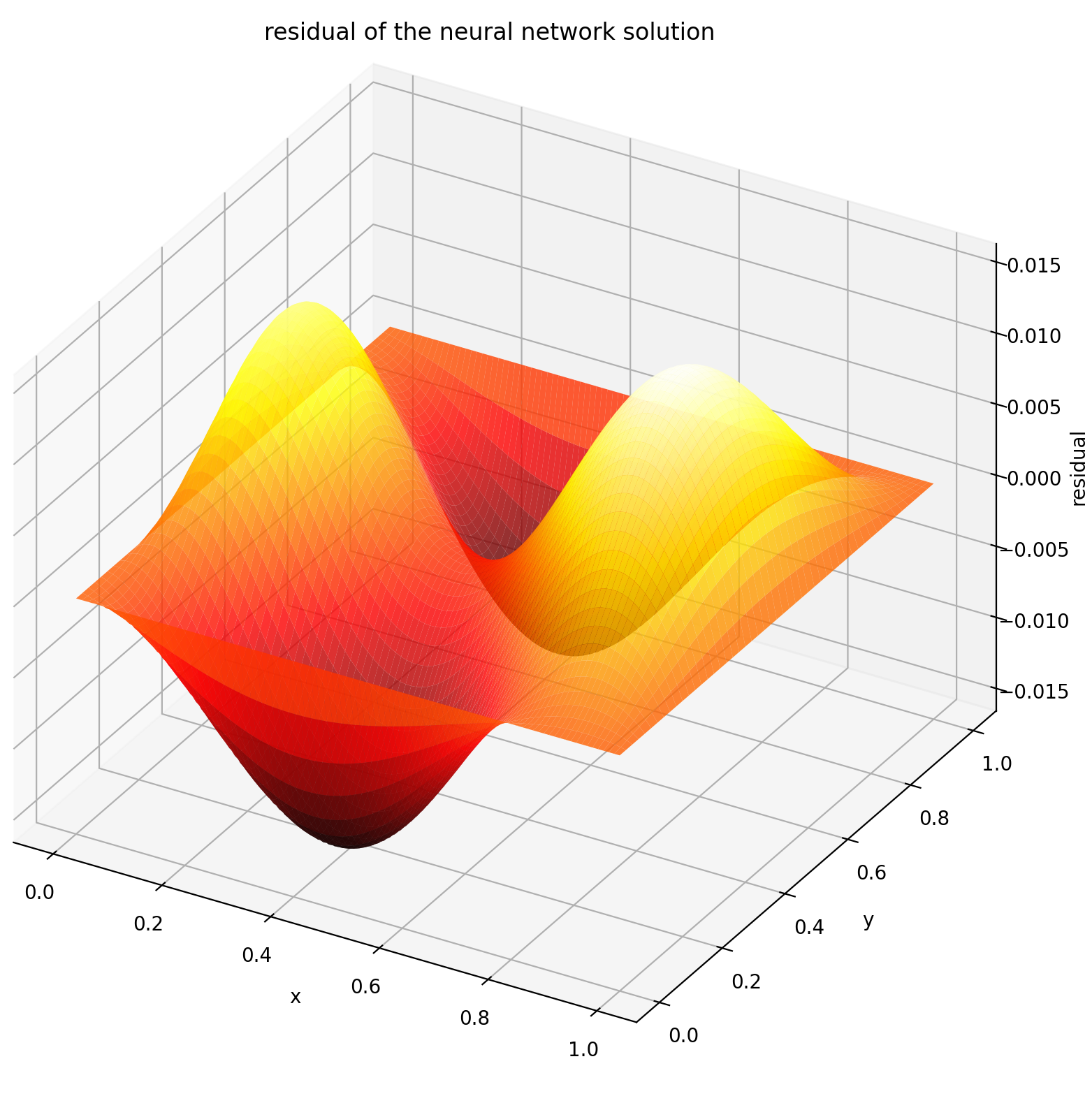 |
Ein Monitor ist ein Tool zur Visualisierung von PDE/ODE-Lösungen sowie der Verlusthistorie und benutzerdefinierten Metriken während des Trainings. Benutzer von Jupyter Notebooks müssen die %matplotlib notebook ausführen. Probieren Sie für Jupyter Lab-Benutzer %matplotlib widget aus.
aus neurodiffeq.monitors import Monitor1D...monitor = Monitor1D(t_min=0.0, t_max=12.0, check_every=100)solver.fit(..., callbacks=[monitor.to_callback()])
Sie sollten sehen, dass die Diagramme alle 100 Epochen sowie in der letzten Epoche aktualisiert werden und zwei Diagramme anzeigen – eines für die Lösungsvisualisierung im Intervall [0,12] und das andere für den Verlustverlauf (Training und Validierung).
Der Einfachheit halber haben wir ein FCNN implementiert – ein vollständig verbundenes neuronales Netzwerk, dessen versteckte Einheiten und Aktivierungsfunktionen angepasst werden können.
aus neurodiffeq.networks import FCNN# Standard: n_input_units=1, n_output_units=1, versteckte_Einheiten=[32, 32], Aktivierung=torch.nn.Tanhnet1 = FCNN(n_input_units=..., n_output_units=..., versteckte_Einheiten=[ ..., ..., ...], Aktivierung=...) ...Netze = [Netz1, Netz2, ...]
FCNN ist normalerweise ein guter Ausgangspunkt. Für fortgeschrittene Benutzer sind Solver mit jedem benutzerdefinierten torch.nn.Module kompatibel. Die einzigen Einschränkungen sind:
Die Module nehmen einen Formtensor (None, n_coords) auf und geben einen Formtensor (None, 1) aus.
Es müssen insgesamt n_funcs -Module in nets vorhanden sein, die an solver = Solver(..., nets=nets) übergeben werden sollen.
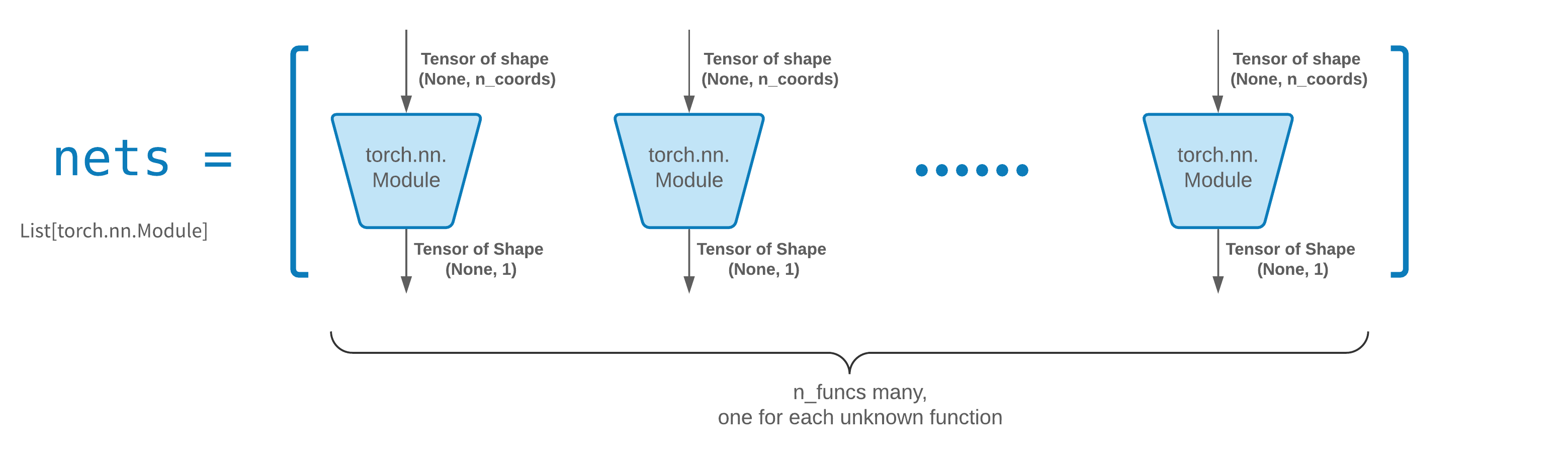
Tatsächlich verfügt neurodiffeq über eine Funktion „single_net“ , die die oben genannten Regeln nicht befolgt und hier nicht behandelt wird.
Lesen Sie das PyTorch-Tutorial zum Aufbau Ihrer eigenen Netzwerkarchitektur (auch Modularchitektur genannt).
Das Transferlernen lässt sich leicht durchführen, indem old_solver.nets (eine Liste von Torch-Modulen) auf der Festplatte serialisiert, dann geladen und an einen neuen Solver übergeben wird:
old_solver.fit(max_epochs=...)# ... speichere „old_solver.nets“ auf der Festplatte# ... lade die Netzwerke von der Festplatte und speichere sie in einigen „loaded_nets“-Variablennew_solver = Solver(..., nets=loaded_nets )new_solver.fit(max_epochs=...)
Wir arbeiten derzeit an Wrapper-Funktionen zum Speichern/Laden von Netzwerken und anderen internen Variablen von Solvers. In der Zwischenzeit können Sie das PyTorch-Tutorial zum Speichern und Laden Ihrer Netzwerke lesen.
In neurodiffeq werden die Netzwerke durch die Minimierung von Verlusten (ODE/PDE-Residuen) trainiert, die an einer Reihe von Punkten in der Domäne ausgewertet werden. Die Punkte werden jedes Mal zufällig neu abgetastet. Um die Anzahl, Verteilung und den Begrenzungsbereich der abgetasteten Punkte zu steuern, können Sie Ihre eigenen Trainings-/ generator angeben.
from neurodiffeq.generators import Generator1D# Default t_min=0.0, t_max=1.0, method='uniform', Noise_std=Noneg1 = Generator1D(size=..., t_min=..., t_max=..., method=.. ., Noise_std=...)g2 = Generator1D(size=..., t_min=..., t_max=..., method=..., Noise_std=...)solver = Solver1D(..., train_generator=g1, valid_generator=g2)
Hier sind einige Beispielverteilungen eines Generator1D .
Generator1D(8192, 0.0, 1.0, method='uniform') | Generator1D(8192, -1.0, 0.0, method='log-spaced-noisy', noise_std=1e-3) |
|---|---|
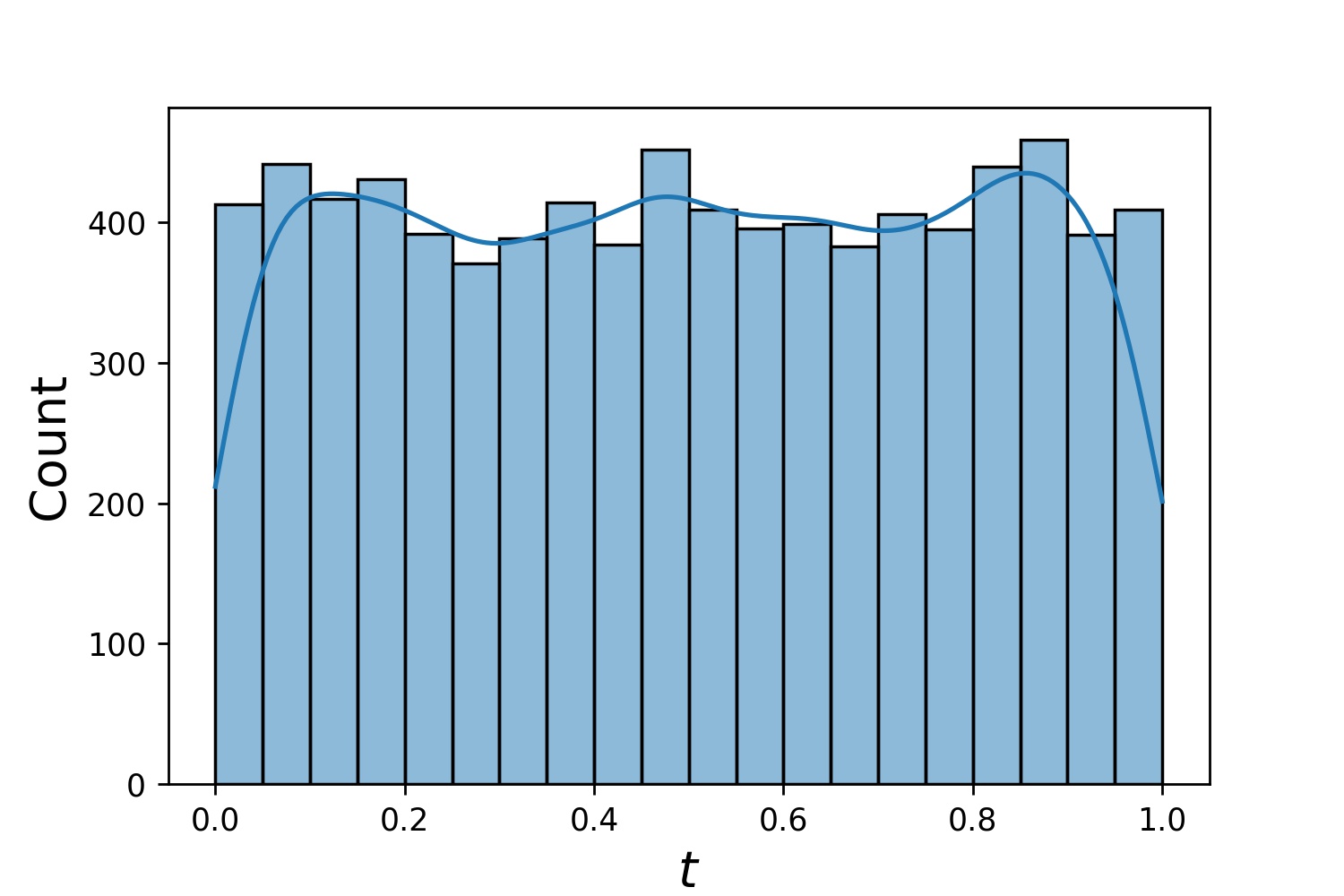 | 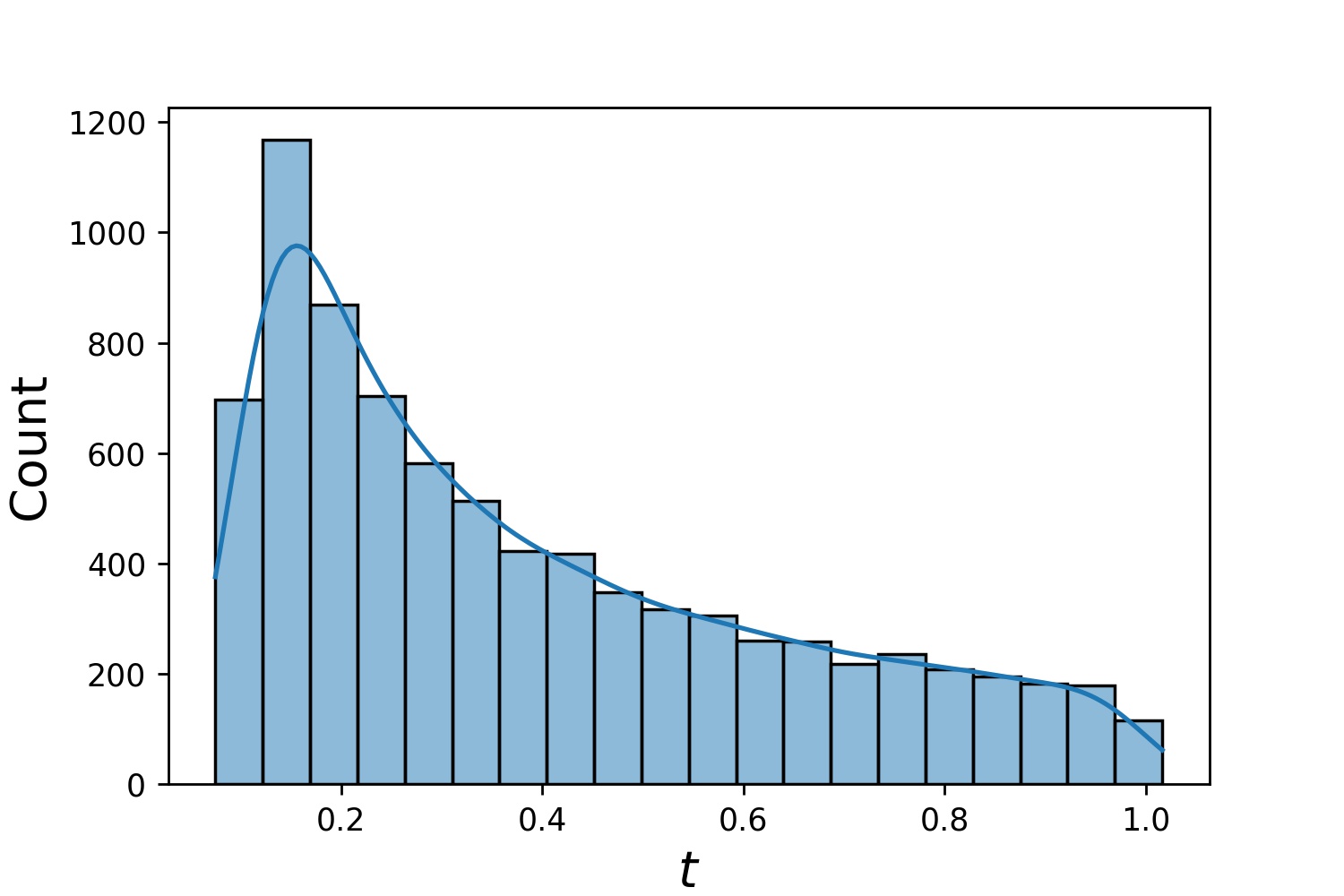 |
Beachten Sie, dass t_min und t_max in Solver1D(...) weggelassen werden können, wenn sowohl train_generator als auch valid_generator angegeben sind. Selbst wenn Sie t_min , t_max , train_generator , valid_generator zusammen übergeben, werden t_min und t_max weiterhin ignoriert.
Ein weiteres nettes Feature der Generatoren ist, dass man sie beispielsweise verketten kann
g1 = Generator2D((16, 16), xy_min=(0, 0), xy_max=(1, 1))g2 = Generator2D((16, 16), xy_min=(1, 1), xy_max=(2, 2 ))g = g1 + g2
Hier ist g ein Generator, der die kombinierten Abtastwerte von g1 und g2 ausgibt
g1 | g2 | g1 + g2 |
|---|---|---|
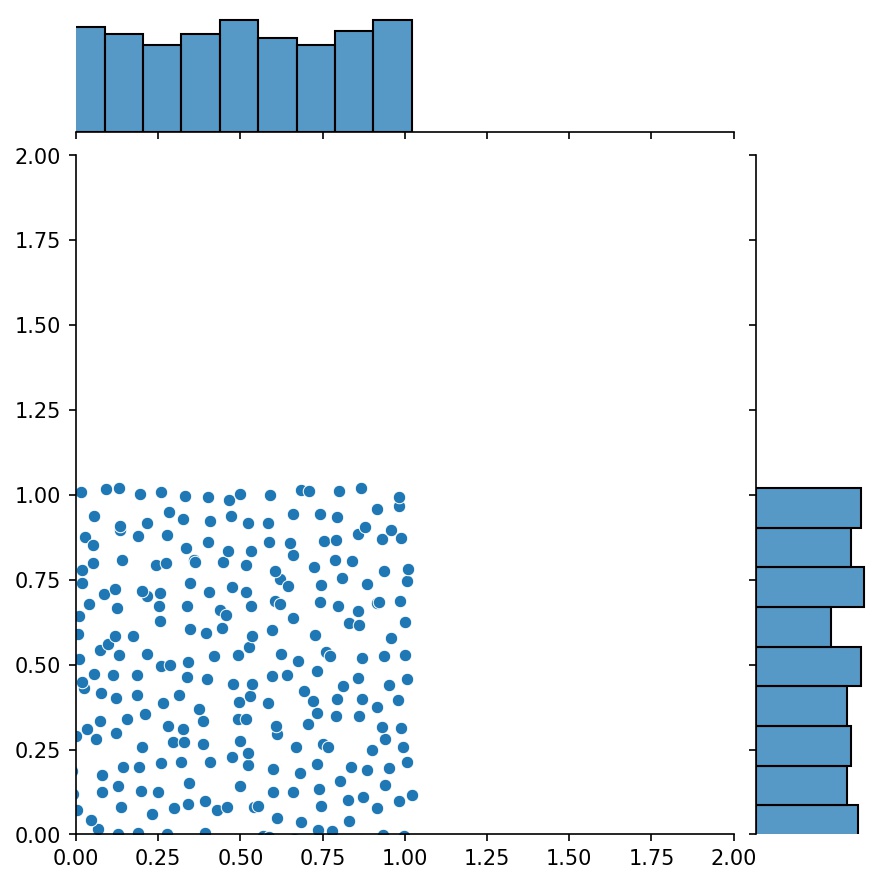 | 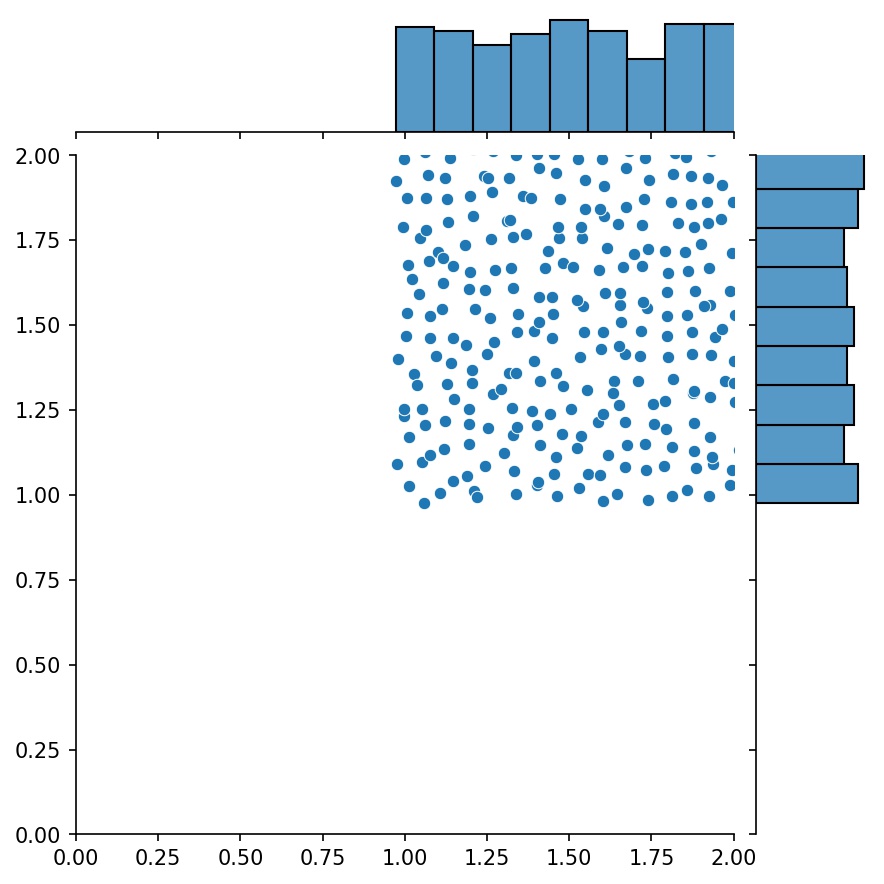 | 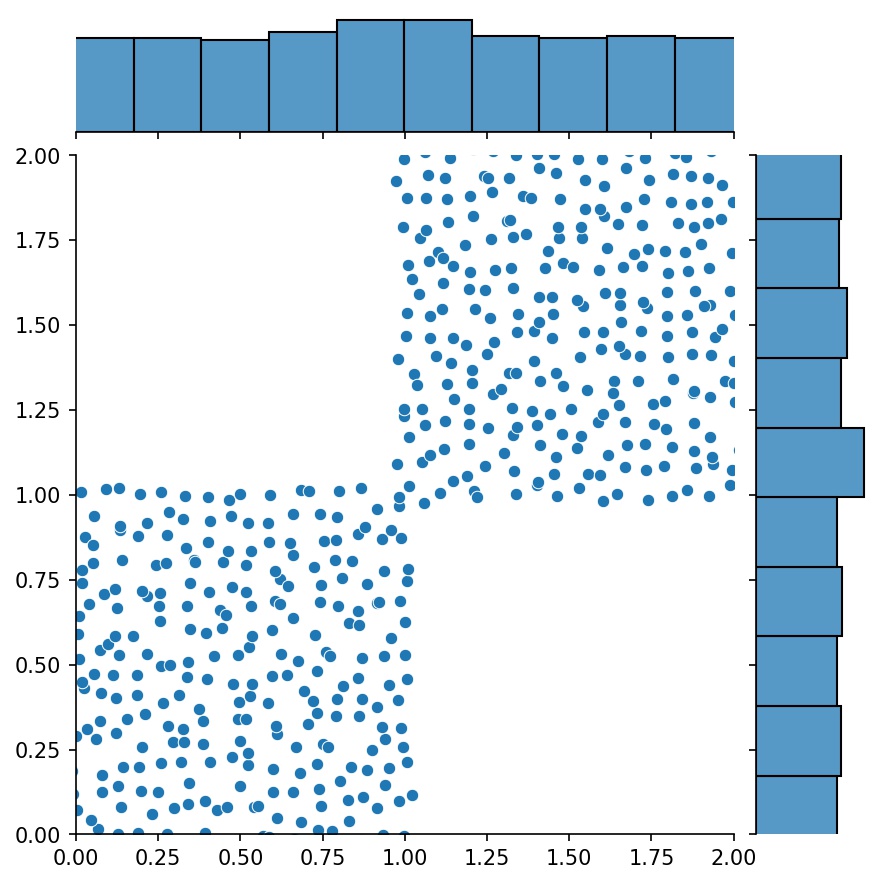 |
Sie können Generator2D , Generator3D usw. verwenden, um Punkte in höheren Dimensionen abzutasten. Aber es gibt auch einen anderen Weg
g1 = Generator1D(1024, 2.0, 3.0, method='uniform')g2 = Generator1D(1024, 0.1, 1.0, method='log-spaced-noisy', Noise_std=0.001)g = g1 * g2
Hier ist g ein Generator, der jedes Mal 1024 Punkte in einem 2D-Rechteck (2,3) × (0.1,1) liefert. Ihre x-Koordinaten werden aus (2,3) mithilfe der Strategie uniform und die y-Koordinaten aus (0.1,1) mithilfe der Strategie log-spaced-noisy ermittelt.
g1 | g2 | g1 * g2 |
|---|---|---|
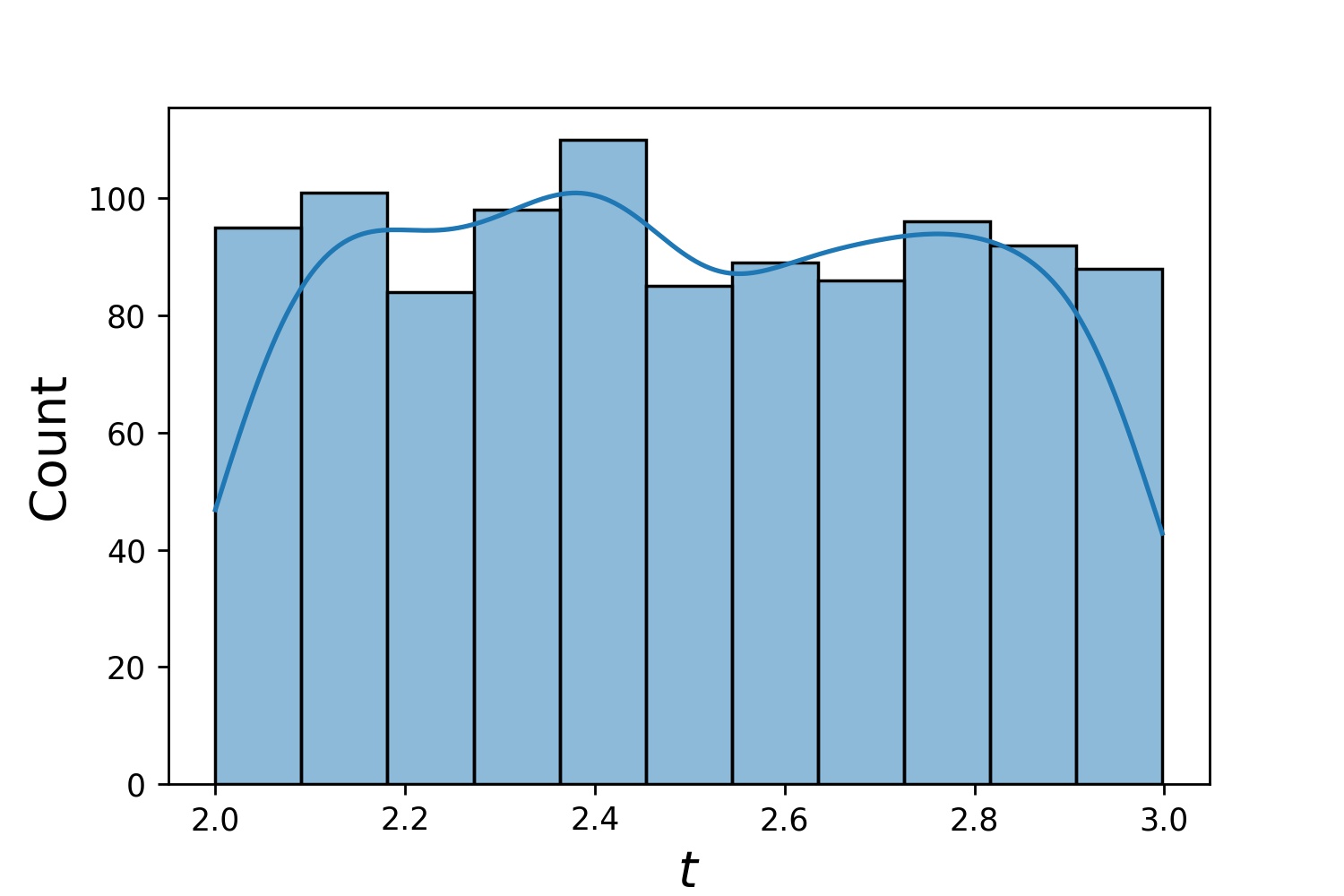 | 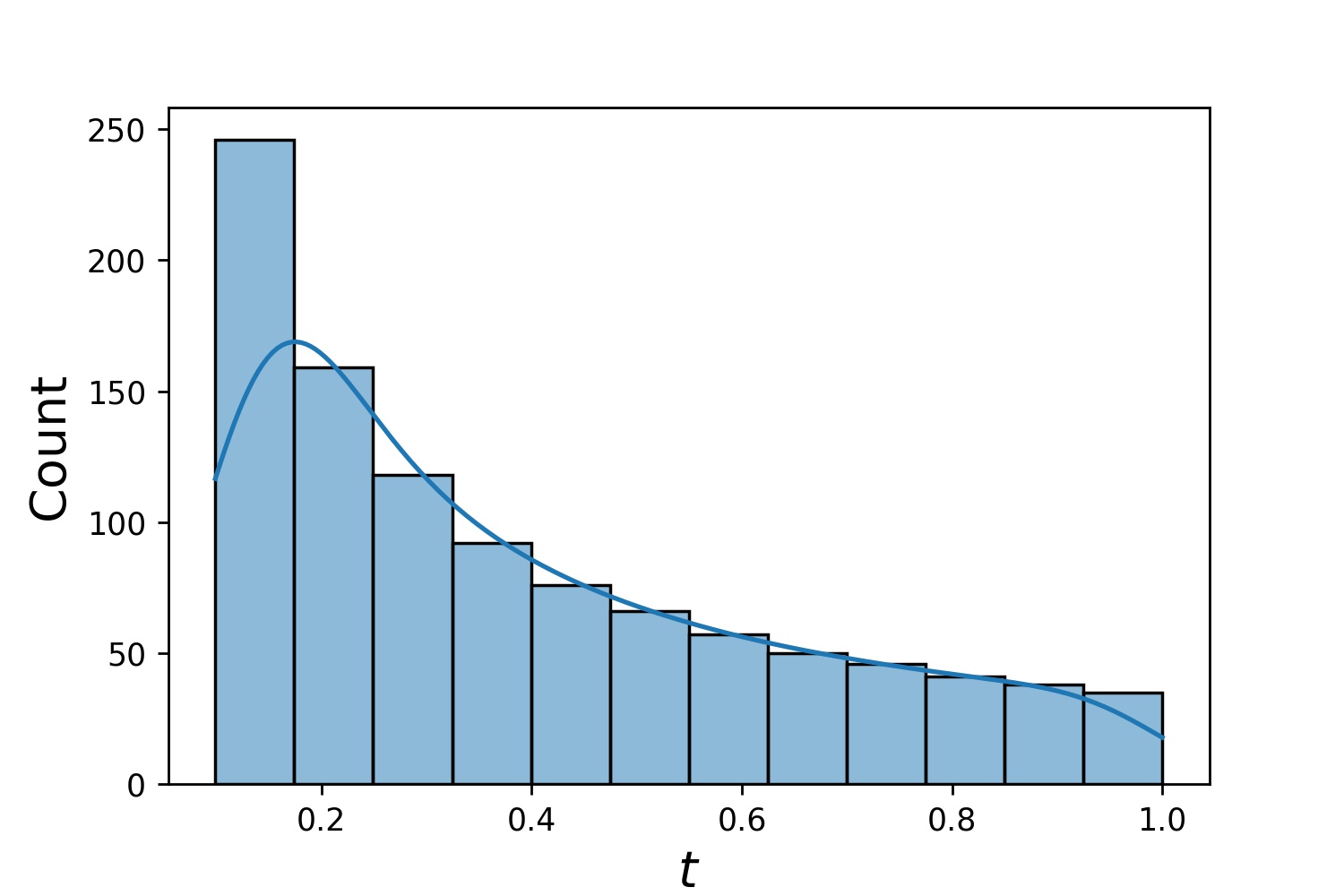 | 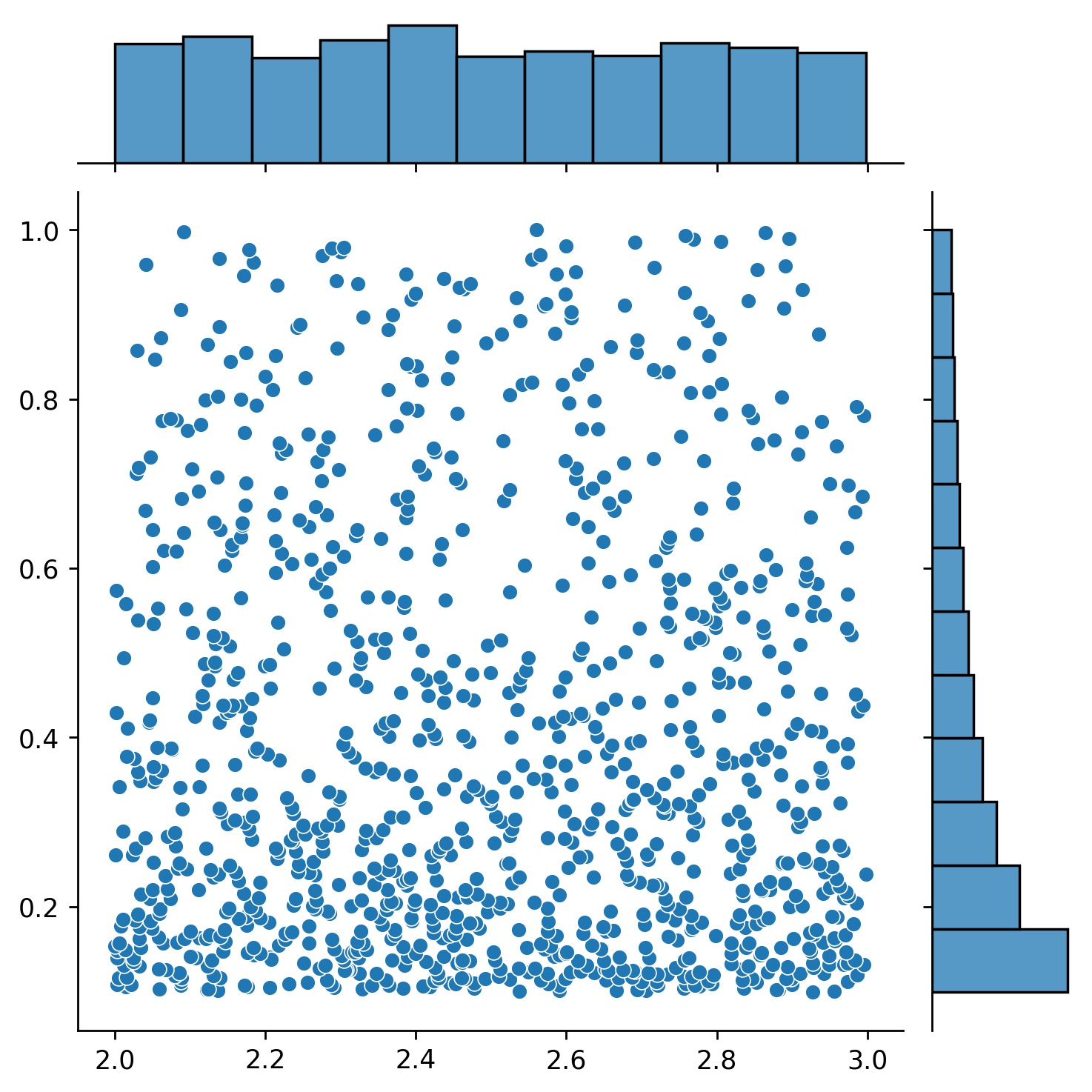 |
Manchmal ist es interessant, ein Bündel von Gleichungen auf einmal zu lösen. Beispielsweise möchten Sie möglicherweise Differentialgleichungen der Form du/dt + λu = 0 unter der Anfangsbedingung u(0) = U0 lösen. Möglicherweise möchten Sie dies für alle λ und U0 auf einmal lösen, indem Sie sie als Eingaben für die neuronalen Netze behandeln.
Eine solche Anwendung sind chemische Reaktionen, bei denen die Reaktionsgeschwindigkeit unbekannt ist. Unterschiedliche Reaktionsgeschwindigkeiten entsprechen unterschiedlichen Lösungen, und nur eine Lösung stimmt mit den beobachteten Datenpunkten überein. Vielleicht möchten Sie zunächst nach einem Bündel von Lösungen suchen und dann die besten Reaktionsgeschwindigkeiten (auch Gleichungsparameter genannt) ermitteln. Der zweite Schritt ist als inverses Problem bekannt.
Hier ist ein Beispiel dafür, wie man dies mit neurodiffeq macht:
Nehmen wir an, wir haben eine Gleichung du/dt + λu = 0 und die Anfangsbedingung u(0) = U0 wobei λ und U0 unbekannte Konstanten sind. Wir haben auch eine Reihe von Beobachtungen t_obs und u_obs . Wir importieren zunächst BundleSolver und BundleIVP die zum Erhalten eines Lösungspakets erforderlich sind:
from neurodiffeq.conditions import BundleIVPfrom neurodiffeq.solvers import BundleSolver1Dimport matplotlib.pyplot as pltimport numpy as npimport Torchfrom neurodiffeq import diff
Wir bestimmen den Bereich der Eingabe t sowie den Bereich der Parameter λ und U0 . Wir müssen auch eine Entscheidung über die Reihenfolge der Parameter treffen. Nämlich, welcher der erste Parameter sein sollte und welcher der zweite sein sollte. Für diese Demo wählen wir λ als ersten Parameter (Index 0) und U0 als zweiten (Index 1). Es ist sehr wichtig, die Indizes der Parameter im Auge zu behalten.
T_MIN, T_MAX = 0, 1LAMBDA_MIN, LAMBDA_MAX = 3, 5 # erster Parameter, Index = 0U0_MIN, U0_MAX = 0,2, 0,6 # zweiter Parameter, Index = 1
Anschließend definieren wir die conditions und solver wie gewohnt, mit der Ausnahme, dass wir BundleIVP und BundleSolver1D anstelle von IVP und Solver1D verwenden. Die Schnittstelle dieser beiden ist IVP und Solver1D sehr ähnlich. Weitere Informationen finden Sie in der API-Referenz.
# Gleichungsparameter kommen nach Eingaben (normalerweise zeitliche und räumliche Koordinaten)diff_eq = lambda u, t, lmd: [diff(u, t) + lmd * u]# Das Schlüsselwortargument muss in BundleIVP „u_0“ heißen. Wenn Sie etwas anderes verwenden, z. B. „y0“, „u0“ usw., funktioniert es nicht.conditions = [BundleIVP(t_0=0, u_0=None, bundle_param_lookup={'u_0': 1}) # u_0 has index 1]solver = BundleSolver1D(ode_system=diff_eq,conditions=conditions,t_min=T_MIN, t_max=T_MAX, theta_min=[LAMBDA_MIN, U0_MIN], # λ hat Index 1theta_max=[LAMBDA_MAX, U0_MAX], # λ hat Index 0; u_0 hat Index 1eq_param_index=(0,), # λ ist der einzige Gleichungsparameter, der den Index 0n_batches_valid=1 hat,
) Da λ ein Parameter in der Gleichung und U0 ein Parameter in der Anfangsbedingung ist , müssen wir λ in diff_eq und U0 in die Bedingung einbeziehen. Wenn ein Parameter sowohl in der Gleichung als auch in der Bedingung vorhanden ist, muss er an beiden Stellen enthalten sein. Alle an BundleSovler1D übergebenen Elemente von conditions müssen Bundle* -Bedingungen sein, auch wenn sie keine Parameter haben.
Jetzt können wir es wie gewohnt trainieren und die Lösung erhalten.
Solver.fit(max_epochs=1000)solution = Solver.get_solution(best=True)
Die Lösung erwartet drei Eingaben – t , λ und U0 . Alle Eingaben müssen die gleiche Form haben. Wenn Sie beispielsweise daran interessiert sind, λ=4 und U0=0.4 festzulegen und die Lösung u gegen t ∈ [0,1] darzustellen, können Sie Folgendes tun
t = np.linspace(0, 1)lmd = 4 * np.ones_like(t)u0 = 0,4 * np.ones_like(t)u = Solution(t, lmd, u0, to_numpy=True)matplotlib.pyplot als pltplt importieren .plot(t, u)
Sobald Sie eine gebündelte solution haben, können Sie einen Parametersatz (λ, U0) finden, der den beobachteten Datenpunkten (t_i, u_i) am ehesten entspricht. Dies wird durch einen einfachen Gradientenabstieg erreicht. Im folgenden Spielzeugbeispiel gehen wir davon aus, dass es nur drei Datenpunkte gibt u(0.2) = 0.273 , u(0.5)=0.129 und u(0.8) = 0.0609 . Das Folgende ist der klassische PyTorch-Workflow.
# beobachtete Datenpunktest_obs = Torch.tensor([0.2, 0.5, 0.8]).reshape(-1, 1)u_obs = Torch.tensor([0.273, 0.129, 0.0609]).reshape(-1, 1)# zufällige Initialisierung von λ und U0; Verfolgen Sie ihren Gradientenlmd_tensor = Torch.rand(1) * (LAMBDA_MAX - LAMBDA_MIN) + LAMBDA_MINu0_tensor = Torch.rand(1) * (U0_MAX - U0_MIN) + U0_MINadam = Torch.optim.Adam([lmd_tensor.requires_grad_(True), u0_tensor.requires_grad_(True)], lr=1e-2)# Gradientenabstieg für 10000 Epochen ausführenfor _ in range(10000):output =solution(t_obs, lmd_tensor * Torch.ones_like(t_obs), u0_tensor * Torch.ones_like(t_obs))loss = ((output - u_obs) ** 2).mean()loss.backward()adam.step()adam.zero_grad()
print(f"λ = {lmd_tensor.item()}, U0={u0_tensor.item()}, loss = {loss.item()}") Einfach. Beim Importieren von neurodiffeq erkennt die Bibliothek automatisch, ob CUDA auf Ihrem Computer verfügbar ist. Da die Bibliothek auf PyTorch basiert, wird der Standard-Tensortyp auf torch.cuda.DoubleTensor gesetzt, wenn ein kompatibles GPU-Gerät gefunden wird.
Weitere Informationen finden Sie in den Abschnitten „Benutzerdefinierte Netzwerke“ und „Transfer-Lernen“.
Der Standard-PyTorch-Weg.
Erstellen Sie Ihre Netzwerke wie unter „Benutzerdefinierte Netzwerke“ erläutert: nets = [FCNN(), FCN(), ...]
Instanziieren Sie einen benutzerdefinierten Optimierer und übergeben Sie ihm alle Parameter dieser Netzwerke
Parameter = [p für Netz in Netze für p in net.parameters()] # Liste der Parameter aller NetzwerkeMY_LEARNING_RATE = 5e-3optimizer = Torch.optim.Adam(Parameters, lr=MY_LEARNING_RATE, ...)
Übergeben Sie BEIDE Ihre nets und Ihren optimizer an den Löser: solver = Solver1D(..., nets=nets, optimizer=optimizer)
Im Gegensatz zu herkömmlichen numerischen Methoden (FEM, FVM usw.) erfordert die NN-basierte Lösung ein gewisses Hypertuning. Die Bibliothek bietet die größtmögliche Flexibilität, jede beliebige Kombination von Hyperparametern auszuprobieren.
Um eine andere Netzwerkarchitektur zu verwenden, können Sie Ihre benutzerdefinierten torch.nn.Module s übergeben.
Um einen anderen Optimierer zu verwenden, können Sie Ihren eigenen Optimierer an solver = Solver(..., optimizer=my_optim) übergeben.
Um eine andere Sampling-Verteilung zu verwenden, können Sie integrierte Generatoren verwenden oder Ihre eigenen Generatoren von Grund auf schreiben.
Um eine andere Stichprobengröße zu verwenden, können Sie die Generatoren optimieren oder solver = Solver(..., n_batches_train) ändern.
Um Hyperparameter während des Trainings dynamisch zu ändern, sehen Sie sich unsere Rückruffunktion an.
Verwenden Sie ReLU nicht zur Aktivierung, da seine Ableitung zweiter Ordnung identisch 0 ist.
Skalieren Sie Ihre PDE/ODE in dimensionsloser Form neu, vorzugsweise alles im Bereich [0,1] . Das Arbeiten mit einer Domäne wie [0,1000000] ist fehleranfällig, da a) PyTorch die Modulgewichte relativ klein initialisiert und b) die meisten Aktivierungsfunktionen (wie Sigmoid, Tanh, Swish) nahe 0 am meisten nichtlinear sind.
Wenn Ihr PDE/ODE zu kompliziert ist, sollten Sie es mit dem Lehrplanlernen versuchen. Beginnen Sie mit dem Training Ihrer Netzwerke auf einer kleineren Domäne und erweitern Sie sie dann schrittweise, bis die gesamte Domäne abgedeckt ist.
Jeder ist herzlich willkommen, zu diesem Projekt beizutragen.
Bei Beiträgen zu diesem Repository berücksichtigen wir den folgenden Prozess:
Öffnen Sie ein Problem, um die Änderung zu besprechen, die Sie vornehmen möchten.
Lesen Sie die Beitragsrichtlinien durch.
Nehmen Sie die Änderung an einem geforkten Repository vor und aktualisieren Sie die README.md, wenn Änderungen an der Schnittstelle vorgenommen werden.
Öffnen Sie eine Pull-Anfrage.