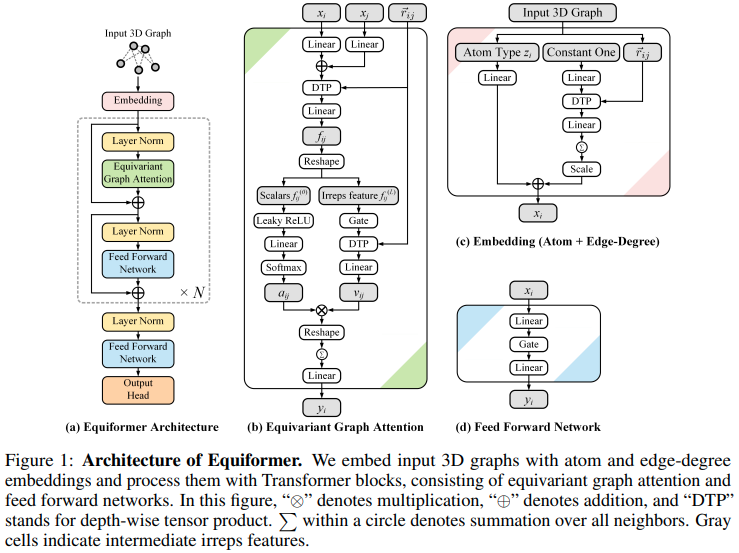
equiformer pytorch herunterladen - equiformer pytorch Quellcode herunterladen

Equiformer – Pytorch (wip)

Implementierung des Equiformer, SE3/E3-Äquivarianten-Aufmerksamkeitsnetzwerks, das neue SOTA erreicht und zur Verwendung durch EquiFold (Prescient Design) für die Proteinfaltung übernommen wird

Das Design scheint auf SE3-Transformern aufzubauen, wobei die Dot-Product-Aufmerksamkeit durch MLP-Aufmerksamkeit und die nichtlineare Nachrichtenübermittlung von GATv2 ersetzt wurde. Für etwas mehr Effizienz wird auch ein Tiefentensorprodukt erstellt. Wenn Sie glauben, dass ich mich irre, schreiben Sie mir bitte eine E-Mail.

Update: Es gab eine neue Entwicklung, die die Skalierung der Gradzahl für SE3-äquivariante Netzwerke erheblich verbessert! In diesem Artikel wurde zunächst darauf hingewiesen, dass durch die Ausrichtung der Darstellungen entlang der Z-Achse (oder gemäß einer anderen Konvention der Y-Achse) die sphärischen Harmonischen dünner werden. Dadurch wird die m _f -Dimension aus der Gleichung entfernt. Ein Folgepapier von Passaro et al. stellte fest, dass auch die Clebsch-Gordan-Matrix dünner geworden ist, was zur Entfernung von m _i und l _f führt. Sie stellten auch den Zusammenhang her, dass das Problem von SO(3) auf SO(2) reduziert wurde, nachdem die Wiederholungen auf einer Achse ausgerichtet wurden. Equiformer v2 (Offizielles Repository) nutzt dies in einem transformatorähnlichen Framework, um neue SOTA zu erreichen.

Ich werde auf jeden Fall noch mehr Arbeit/Erkundung hineinstecken. Vorerst habe ich die Tricks aus den ersten beiden Artikeln für Equiformer v1 übernommen, abgesehen von der vollständigen Konvertierung in SO(2).

Update 2: Es scheint ein neues SOTA ohne Interaktion zwischen Wiederholungen höheren Grades zu geben (mit anderen Worten, alle Tensorprodukt-/Clebsch-Gordan-Mathematik entfällt). GotenNet, das eine transformatorische Version von HEGNN zu sein scheint

Installieren

$ pip install equiformer-pytorch

Verwendung

 import torch
from equiformer_pytorch import Equiformer

model = Equiformer (
    num_tokens = 24 ,
    dim = ( 4 , 4 , 2 ),               # dimensions per type, ascending, length must match number of degrees (num_degrees)
    dim_head = ( 4 , 4 , 4 ),          # dimension per attention head
    heads = ( 2 , 2 , 2 ),             # number of attention heads
    num_linear_attn_heads = 0 ,     # number of global linear attention heads, can see all the neighbors
    num_degrees = 3 ,               # number of degrees
    depth = 4 ,                     # depth of equivariant transformer
    attend_self = True ,            # attending to self or not
    reduce_dim_out = True ,         # whether to reduce out to dimension of 1, say for predicting new coordinates for type 1 features
    l2_dist_attention = False      # set to False to try out MLP attention
). cuda ()

feats = torch . randint ( 0 , 24 , ( 1 , 128 )). cuda ()
coors = torch . randn ( 1 , 128 , 3 ). cuda ()
mask  = torch . ones ( 1 , 128 ). bool (). cuda ()

out = model ( feats , coors , mask ) # (1, 128)

out . type0 # invariant type 0    - (1, 128)
out . type1 # equivariant type 1  - (1, 128, 3)

Dieses Repository enthält auch eine Möglichkeit, die Speichernutzung mithilfe reversibler Netzwerke von der Tiefe zu entkoppeln. Mit anderen Worten: Wenn Sie die Tiefe erhöhen, bleiben die Speicherkosten bei der Verwendung eines äquiformeren Transformatorblocks (Aufmerksamkeit und Feedforward) konstant.

 import torch
from equiformer_pytorch import Equiformer

model = Equiformer (
    num_tokens = 24 ,
    dim = ( 4 , 4 , 2 ),
    dim_head = ( 4 , 4 , 4 ),
    heads = ( 2 , 2 , 2 ),
    num_degrees = 3 ,
    depth = 48 ,          # depth of 48 - just to show that it runs - in reality, seems to be quite unstable at higher depths, so architecture stil needs more work
    reversible = True ,   # just set this to True to use https://arxiv.org/abs/1707.04585
). cuda ()

feats = torch . randint ( 0 , 24 , ( 1 , 128 )). cuda ()
coors = torch . randn ( 1 , 128 , 3 ). cuda ()
mask  = torch . ones ( 1 , 128 ). bool (). cuda ()

out = model ( feats , coors , mask )

out . type0 . sum (). backward ()

Kanten

mit Kanten, z.B. Atombindungen

 import torch
from equiformer_pytorch import Equiformer

model = Equiformer (
    num_tokens = 28 ,
    dim = 64 ,
    num_edge_tokens = 4 ,       # number of edge type, say 4 bond types
    edge_dim = 16 ,             # dimension of edge embedding
    depth = 2 ,
    input_degrees = 1 ,
    num_degrees = 3 ,
    reduce_dim_out = True
)

atoms = torch . randint ( 0 , 28 , ( 2 , 32 ))
bonds = torch . randint ( 0 , 4 , ( 2 , 32 , 32 ))
coors = torch . randn ( 2 , 32 , 3 )
mask  = torch . ones ( 2 , 32 ). bool ()

out = model ( atoms , coors , mask , edges = bonds )

out . type0 # (2, 32)
out . type1 # (2, 32, 3)

mit Adjazenzmatrix

 import torch
from equiformer_pytorch import Equiformer

model = Equiformer (
    dim = 32 ,
    heads = 8 ,
    depth = 1 ,
    dim_head = 64 ,
    num_degrees = 2 ,
    valid_radius = 10 ,
    reduce_dim_out = True ,
    attend_sparse_neighbors = True ,  # this must be set to true, in which case it will assert that you pass in the adjacency matrix
    num_neighbors = 0 ,               # if you set this to 0, it will only consider the connected neighbors as defined by the adjacency matrix. but if you set a value greater than 0, it will continue to fetch the closest points up to this many, excluding the ones already specified by the adjacency matrix
    num_adj_degrees_embed = 2 ,       # this will derive the second degree connections and embed it correctly
    max_sparse_neighbors = 8         # you can cap the number of neighbors, sampled from within your sparse set of neighbors as defined by the adjacency matrix, if specified
)

feats = torch . randn ( 1 , 128 , 32 )
coors = torch . randn ( 1 , 128 , 3 )
mask  = torch . ones ( 1 , 128 ). bool ()

# placeholder adjacency matrix
# naively assuming the sequence is one long chain (128, 128)

i = torch . arange ( 128 )
adj_mat = ( i [:, None ] <= ( i [ None , :] + 1 )) & ( i [:, None ] >= ( i [ None , :] - 1 ))

out = model ( feats , coors , mask , adj_mat = adj_mat )

out . type0 # (1, 128)
out . type1 # (1, 128, 3)

Anerkennung

StabilityAI für das großzügige Sponsoring sowie meine anderen Sponsoren da draußen

Testen

Tests auf Äquivarianz usw

$ python setup.py test

Beispiel

Installieren Sie zuerst sidechainnet

$ pip install sidechainnet

Führen Sie dann die Aufgabe zur Rauschunterdrückung des Protein-Backbones aus

$ python denoise.py

Todo

Zitate

 @article { Liao2022EquiformerEG ,
    title   = { Equiformer: Equivariant Graph Attention Transformer for 3D Atomistic Graphs } ,
    author  = { Yi Liao and Tess E. Smidt } ,
    journal = { ArXiv } ,
    year    = { 2022 } ,
    volume  = { abs/2206.11990 }
}

 @article { Lee2022.10.07.511322 ,
    author  = { Lee, Jae Hyeon and Yadollahpour, Payman and Watkins, Andrew and Frey, Nathan C. and Leaver-Fay, Andrew and Ra, Stephen and Cho, Kyunghyun and Gligorijevic, Vladimir and Regev, Aviv and Bonneau, Richard } ,
    title   = { EquiFold: Protein Structure Prediction with a Novel Coarse-Grained Structure Representation } ,
    elocation-id = { 2022.10.07.511322 } ,
    year    = { 2022 } ,
    doi     = { 10.1101/2022.10.07.511322 } ,
    publisher = { Cold Spring Harbor Laboratory } ,
    URL     = { https://www.biorxiv.org/content/early/2022/10/08/2022.10.07.511322 } ,
    eprint  = { https://www.biorxiv.org/content/early/2022/10/08/2022.10.07.511322.full.pdf } ,
    journal = { bioRxiv }
}

 @article { Shazeer2019FastTD ,
    title   = { Fast Transformer Decoding: One Write-Head is All You Need } ,
    author  = { Noam M. Shazeer } ,
    journal = { ArXiv } ,
    year    = { 2019 } ,
    volume  = { abs/1911.02150 }
}

 @misc { ding2021cogview ,
    title   = { CogView: Mastering Text-to-Image Generation via Transformers } ,
    author  = { Ming Ding and Zhuoyi Yang and Wenyi Hong and Wendi Zheng and Chang Zhou and Da Yin and Junyang Lin and Xu Zou and Zhou Shao and Hongxia Yang and Jie Tang } ,
    year    = { 2021 } ,
    eprint  = { 2105.13290 } ,
    archivePrefix = { arXiv } ,
    primaryClass = { cs.CV }
}

 @inproceedings { Kim2020TheLC ,
    title   = { The Lipschitz Constant of Self-Attention } ,
    author  = { Hyunjik Kim and George Papamakarios and Andriy Mnih } ,
    booktitle = { International Conference on Machine Learning } ,
    year    = { 2020 }
}

 @article { Zitnick2022SphericalCF ,
    title   = { Spherical Channels for Modeling Atomic Interactions } ,
    author  = { C. Lawrence Zitnick and Abhishek Das and Adeesh Kolluru and Janice Lan and Muhammed Shuaibi and Anuroop Sriram and Zachary W. Ulissi and Brandon C. Wood } ,
    journal = { ArXiv } ,
    year    = { 2022 } ,
    volume  = { abs/2206.14331 }
}

 @article { Passaro2023ReducingSC ,
  title     = { Reducing SO(3) Convolutions to SO(2) for Efficient Equivariant GNNs } ,
  author    = { Saro Passaro and C. Lawrence Zitnick } ,
  journal   = { ArXiv } ,
  year      = { 2023 } ,
  volume    = { abs/2302.03655 }
}

 @inproceedings { Gomez2017TheRR ,
    title   = { The Reversible Residual Network: Backpropagation Without Storing Activations } ,
    author  = { Aidan N. Gomez and Mengye Ren and Raquel Urtasun and Roger Baker Grosse } ,
    booktitle = { NIPS } ,
    year    = { 2017 }
}

 @article { Bondarenko2023QuantizableTR ,
    title   = { Quantizable Transformers: Removing Outliers by Helping Attention Heads Do Nothing } ,
    author  = { Yelysei Bondarenko and Markus Nagel and Tijmen Blankevoort } ,
    journal = { ArXiv } ,
    year    = { 2023 } ,
    volume  = { abs/2306.12929 } ,
    url     = { https://api.semanticscholar.org/CorpusID:259224568 }
}

 @inproceedings { Arora2023ZoologyMA ,
  title   = { Zoology: Measuring and Improving Recall in Efficient Language Models } ,
  author  = { Simran Arora and Sabri Eyuboglu and Aman Timalsina and Isys Johnson and Michael Poli and James Zou and Atri Rudra and Christopher R'e } ,
  year    = { 2023 } ,
  url     = { https://api.semanticscholar.org/CorpusID:266149332 }
}