Eine Implementierung des Minimax-KI-Algorithmus im Tic-Tac-Toe-Spiel (oder Noughts and Crosses-Spiel). Probieren Sie es aus: Tic-Tac-Toe - Minimax
Um Spiele mithilfe von KI zu lösen, führen wir das Konzept eines Spielbaums gefolgt von einem Minimax-Algorithmus ein. Die verschiedenen Zustände des Spiels werden durch Knoten im Spielbaum dargestellt, sehr ähnlich den oben genannten Planungsproblemen. Die Idee ist nur etwas anders. Im Spielbaum sind die Knoten in Ebenen angeordnet, die den Spielzügen jedes Spielers entsprechen, sodass der „Wurzel“-Knoten des Baums (normalerweise oben im Diagramm dargestellt) die Anfangsposition im Spiel darstellt. Bei Tic-Tac-Toe wäre dies das leere Raster, auf dem noch keine Xs oder Os gespielt wurden. Unter Wurzel, auf der zweiten Ebene, befinden sich die möglichen Zustände, die sich aus den Zügen des ersten Spielers ergeben können, sei es X oder O. Wir nennen diese Knoten die „Kinder“ des Wurzelknotens.
Jeder Knoten auf der zweiten Ebene hätte außerdem als untergeordnete Knoten die Zustände, die von ihm aus durch die Bewegungen des gegnerischen Spielers erreicht werden können. Dies wird Level für Level fortgesetzt, bis Zustände erreicht werden, in denen das Spiel beendet ist. Beim Tic-Tac-Toe bedeutet das, dass entweder einer der Spieler eine Dreierreihe bekommt und gewinnt, oder das Spielbrett voll ist und das Spiel unentschieden endet.
Minimax ist eine künstliche Intelligenz, die in Spielen für zwei Spieler wie Tic-Tac-Toe, Dame, Schach und Go eingesetzt wird. Diese Spiele werden als Nullsummenspiele bezeichnet, weil in einer mathematischen Darstellung: ein Spieler gewinnt (+1) und der andere Spieler verliert (-1) oder beide Spieler nicht gewinnen (0).
Der Algorithmus sucht rekursiv nach dem besten Zug, der dazu führt, dass der Max -Spieler gewinnt oder nicht verliert (Unentschieden). Es berücksichtigt den aktuellen Status des Spiels und die verfügbaren Züge in diesem Status und führt dann jeden gültigen Zug aus (abwechselnd Min. und Max. ), bis ein Endstatus gefunden wird (Gewinnen, Unentschieden oder Verlieren).
Der Algorithmus wurde im Buch Algorithms in a Nutshell (George Heineman; Gary Pollice; Stanley Selkow, 2009) untersucht. Pseudocode (angepasst):
minimax(state, depth, player)
if (player = max) then
best = [null, -infinity]
else
best = [null, +infinity]
if (depth = 0 or gameover) then
score = evaluate this state for player
return [null, score]
for each valid move m for player in state s do
execute move m on s
[move, score] = minimax(s, depth - 1, -player)
undo move m on s
if (player = max) then
if score > best.score then best = [move, score]
else
if score < best.score then best = [move, score]
return best
end
Jetzt sehen wir jeden Teil dieses Pseudocodes mit Python-Implementierung. Die Python-Implementierung ist in diesem Repository verfügbar. Bedenken Sie zunächst Folgendes:
Brett = [ [0, 0, 0], [0, 0, 0], [0, 0, 0] ]
MAX = +1
MIN = -1
Der MAX kann X oder O sein und der MIN kann O oder X sein, was auch immer. Das Brett ist 3x3.
def minimax ( state , depth , player ): if player == MAX :
return [ - 1 , - 1 , - infinity ]
else :
return [ - 1 , - 1 , + infinity ]Beide Spieler beginnen mit Ihrem schlechtesten Ergebnis. Wenn der Spieler MAX ist, beträgt seine Punktzahl -unendlich. Wenn der Spieler andernfalls MIN ist, beträgt seine Punktzahl +unendlich. Hinweis: infinity ist ein Alias für inf (aus dem Mathematikmodul in Python).
Der beste Zug auf dem Brett ist [-1, -1] (Zeile und Spalte) für alle.
if depth == 0 or game_over ( state ):
score = evaluate ( state )
return scoreWenn die Tiefe gleich Null ist, gibt es auf dem Spielbrett keine neuen leeren Zellen zum Ausspielen. Oder wenn ein Spieler gewinnt, endet das Spiel für MAX oder MIN. Daher wird die Punktzahl für diesen Staat zurückgegeben.
Jetzt sehen wir den Hauptteil dieses Codes, der die Rekursion enthält.
for cell in empty_cells ( state ):
x , y = cell [ 0 ], cell [ 1 ]
state [ x ][ y ] = player
score = minimax ( state , depth - 1 , - player )
state [ x ][ y ] = 0
score [ 0 ], score [ 1 ] = x , yFür jeden gültigen Zug (leere Zellen):
Der Zug (+1 oder -1) auf dem Brett wird rückgängig gemacht und die Zeile und Spalte werden eingesammelt.
Der nächste Schritt besteht darin, die Punktzahl mit der Besten zu vergleichen.
if player == MAX :
if score [ 2 ] > best [ 2 ]:
best = score
else :
if score [ 2 ] < best [ 2 ]:
best = scoreFür MAX-Spieler wird eine höhere Punktzahl erzielt. Für einen MIN-Spieler wird eine niedrigere Punktzahl erzielt. Und am Ende wird der beste Zug zurückgegeben. Endgültiger Algorithmus:
def minimax ( state , depth , player ):
if player == MAX :
best = [ - 1 , - 1 , - infinity ]
else :
best = [ - 1 , - 1 , + infinity ]
if depth == 0 or game_over ( state ):
score = evaluate ( state )
return [ - 1 , - 1 , score ]
for cell in empty_cells ( state ):
x , y = cell [ 0 ], cell [ 1 ]
state [ x ][ y ] = player
score = minimax ( state , depth - 1 , - player )
state [ x ][ y ] = 0
score [ 0 ], score [ 1 ] = x , y
if player == MAX :
if score [ 2 ] > best [ 2 ]:
best = score
else :
if score [ 2 ] < best [ 2 ]:
best = score
return best Unten ist die beste Bewegung in der Mitte, da der Maximalwert am 2. Knoten links liegt.
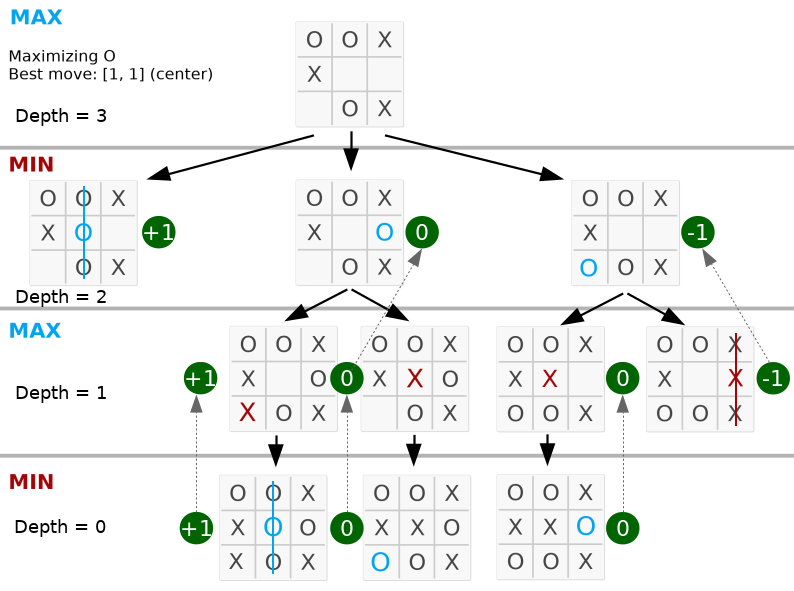
Achten Sie darauf, dass die Tiefe den gültigen Zügen auf dem Brett entspricht. Der vollständige Code ist in py_version/ verfügbar.
Vereinfachter Spielbaum:
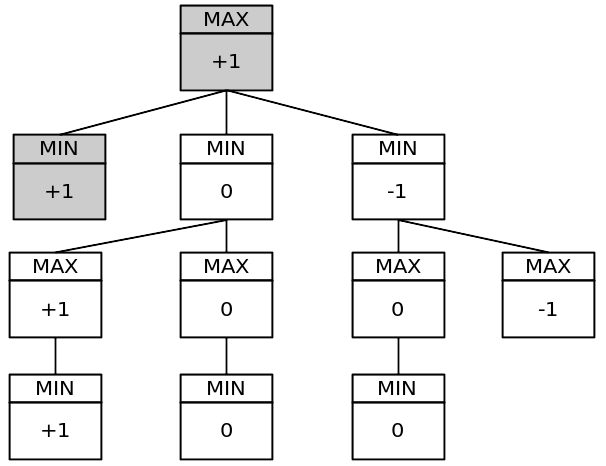
Dieser Baum hat 11 Knoten. Der vollständige Spielbaum hat 549.946 Knoten! Sie können es testen, indem Sie eine statische globale Variable in Ihr Programm einfügen und diese für jeden Minimax-Funktionsaufruf pro Runde erhöhen.
Bei einem komplexeren Spiel wie Schach ist es schwierig, den gesamten Spielbaum zu durchsuchen. Allerdings ist Alpha-Beta-Pruning eine Optimierungsmethode für den Minimax-Algorithmus, die es uns ermöglicht, einige Zweige im Suchbaum zu ignorieren, da er bei der Suche irrelevante Knoten (Teilbäume) schneidet. Weitere Informationen finden Sie unter: