se3 transformer pytorch

SE3-Transformator – Pytorch

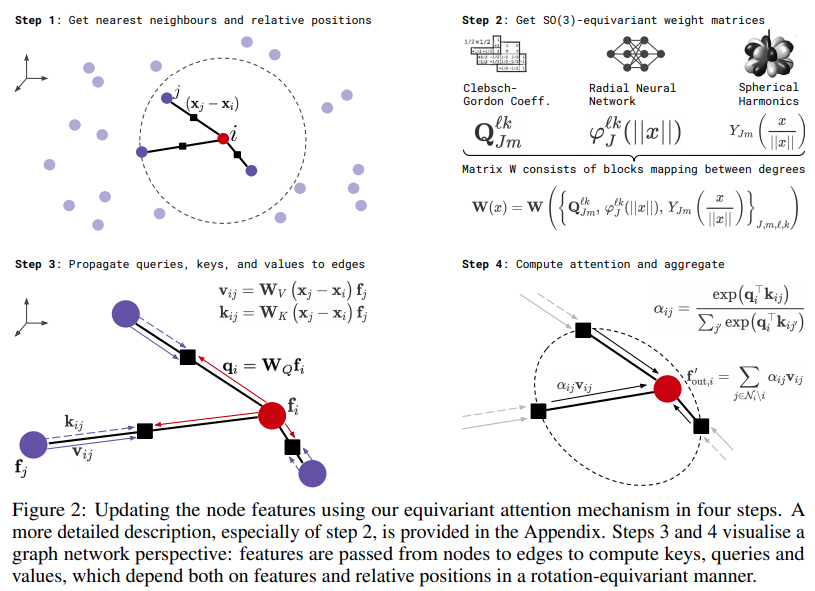
Implementierung von SE3-Transformatoren für äquivariante Selbstaufmerksamkeit in Pytorch. Wird möglicherweise für die Replikation von Alphafold2-Ergebnissen und anderen Anwendungen in der Arzneimittelforschung benötigt.

Beispiel für Äquivarianz

Wenn Sie eine Version von SE3 Transformers vor Version 0.6.0 verwendet haben, aktualisieren Sie diese bitte. Ein großer Fehler wurde von @MattMcPartlon aufgedeckt, wenn Sie nicht die Adjacency-Sparse-Neighbors-Einstellungen verwendet haben und sich auf die Funktionalität der Nearest Neighbors verlassen haben

Update: Es wird empfohlen, stattdessen Equiformer zu verwenden

Installieren

$ pip install se3-transformer-pytorch

Verwendung

 import torch
from se3_transformer_pytorch import SE3Transformer

model = SE3Transformer (
    dim = 512 ,
    heads = 8 ,
    depth = 6 ,
    dim_head = 64 ,
    num_degrees = 4 ,
    valid_radius = 10
)

feats = torch . randn ( 1 , 1024 , 512 )
coors = torch . randn ( 1 , 1024 , 3 )
mask  = torch . ones ( 1 , 1024 ). bool ()

out = model ( feats , coors , mask ) # (1, 1024, 512)

Mögliche Beispielverwendung in Alphafold2, wie hier beschrieben

 import torch
from se3_transformer_pytorch import SE3Transformer

model = SE3Transformer (
    dim = 64 ,
    depth = 2 ,
    input_degrees = 1 ,
    num_degrees = 2 ,
    output_degrees = 2 ,
    reduce_dim_out = True ,
    differentiable_coors = True
)

atom_feats = torch . randn ( 2 , 32 , 64 )
coors = torch . randn ( 2 , 32 , 3 )
mask  = torch . ones ( 2 , 32 ). bool ()

refined_coors = coors + model ( atom_feats , coors , mask , return_type = 1 ) # (2, 32, 3)

Sie können die Basistransformatorklasse auch mit der Einbettung der übergebenen Typ-0-Features beauftragen. Vorausgesetzt, es handelt sich um Atome

 import torch
from se3_transformer_pytorch import SE3Transformer

model = SE3Transformer (
    num_tokens = 28 ,       # 28 unique atoms
    dim = 64 ,
    depth = 2 ,
    input_degrees = 1 ,
    num_degrees = 2 ,
    output_degrees = 2 ,
    reduce_dim_out = True
)

atoms = torch . randint ( 0 , 28 , ( 2 , 32 ))
coors = torch . randn ( 2 , 32 , 3 )
mask  = torch . ones ( 2 , 32 ). bool ()

refined_coors = coors + model ( atoms , coors , mask , return_type = 1 ) # (2, 32, 3)

Wenn Sie der Meinung sind, dass das Netz von der Positionskodierung weiter profitieren könnte, können Sie Ihre Positionen im Raum kennzeichnen und wie folgt übergeben.

 import torch
from se3_transformer_pytorch import SE3Transformer

model = SE3Transformer (
    dim = 64 ,
    depth = 2 ,
    input_degrees = 2 ,
    num_degrees = 2 ,
    output_degrees = 2 ,
    reduce_dim_out = True  # reduce out the final dimension
)

atom_feats  = torch . randn ( 2 , 32 , 64 , 1 ) # b x n x d x type0
coors_feats = torch . randn ( 2 , 32 , 64 , 3 ) # b x n x d x type1

# atom features are type 0, predicted coordinates are type 1
features = { '0' : atom_feats , '1' : coors_feats }
coors = torch . randn ( 2 , 32 , 3 )
mask  = torch . ones ( 2 , 32 ). bool ()

refined_coors = coors + model ( features , coors , mask , return_type = 1 ) # (2, 32, 3) - equivariant to input type 1 features and coordinates 

Kanten

Um SE3-Transformern Kanteninformationen (z. B. Bindungstypen zwischen Atomen) bereitzustellen, müssen Sie bei der Initialisierung lediglich zwei weitere Schlüsselwortargumente übergeben.

 import torch
from se3_transformer_pytorch import SE3Transformer

model = SE3Transformer (
    num_tokens = 28 ,
    dim = 64 ,
    num_edge_tokens = 4 ,       # number of edge type, say 4 bond types
    edge_dim = 16 ,             # dimension of edge embedding
    depth = 2 ,
    input_degrees = 1 ,
    num_degrees = 3 ,
    output_degrees = 1 ,
    reduce_dim_out = True
)

atoms = torch . randint ( 0 , 28 , ( 2 , 32 ))
bonds = torch . randint ( 0 , 4 , ( 2 , 32 , 32 ))
coors = torch . randn ( 2 , 32 , 3 )
mask  = torch . ones ( 2 , 32 ). bool ()

pred = model ( atoms , coors , mask , edges = bonds , return_type = 0 ) # (2, 32, 1)

Wenn Sie kontinuierliche Werte für Ihre Kanten übergeben möchten, können Sie num_edge_tokens nicht festlegen, Ihre diskreten Bindungstypen codieren und diese dann mit den Fourier-Merkmalen dieser kontinuierlichen Werte verknüpfen

 import torch
from se3_transformer_pytorch import SE3Transformer
from se3_transformer_pytorch . utils import fourier_encode

model = SE3Transformer (
    dim = 64 ,
    depth = 1 ,
    attend_self = True ,
    num_degrees = 2 ,
    output_degrees = 2 ,
    edge_dim = 34           # edge dimension must match the final dimension of the edges being passed in
)

feats = torch . randn ( 1 , 32 , 64 )
coors = torch . randn ( 1 , 32 , 3 )
mask  = torch . ones ( 1 , 32 ). bool ()

pairwise_continuous_values = torch . randint ( 0 , 4 , ( 1 , 32 , 32 , 2 ))  # say there are 2

edges = fourier_encode (
    pairwise_continuous_values ,
    num_encodings = 8 ,
    include_self = True
) # (1, 32, 32, 34) - {2 * (2 * 8 + 1)}

out = model ( feats , coors , mask , edges = edges , return_type = 1 )

Spärliche Nachbarn

Wenn Sie die Konnektivität Ihrer Punkte kennen (z. B. Sie arbeiten mit Molekülen), können Sie eine Adjazenzmatrix in Form einer booleschen Maske übergeben (wobei True die Konnektivität angibt).

 import torch
from se3_transformer_pytorch import SE3Transformer

model = SE3Transformer (
    dim = 32 ,
    heads = 8 ,
    depth = 1 ,
    dim_head = 64 ,
    num_degrees = 2 ,
    valid_radius = 10 ,
    attend_sparse_neighbors = True ,  # this must be set to true, in which case it will assert that you pass in the adjacency matrix
    num_neighbors = 0 ,               # if you set this to 0, it will only consider the connected neighbors as defined by the adjacency matrix. but if you set a value greater than 0, it will continue to fetch the closest points up to this many, excluding the ones already specified by the adjacency matrix
    max_sparse_neighbors = 8         # you can cap the number of neighbors, sampled from within your sparse set of neighbors as defined by the adjacency matrix, if specified
)

feats = torch . randn ( 1 , 128 , 32 )
coors = torch . randn ( 1 , 128 , 3 )
mask  = torch . ones ( 1 , 128 ). bool ()

# placeholder adjacency matrix
# naively assuming the sequence is one long chain (128, 128)

i = torch . arange ( 128 )
adj_mat = ( i [:, None ] <= ( i [ None , :] + 1 )) & ( i [:, None ] >= ( i [ None , :] - 1 ))

out = model ( feats , coors , mask , adj_mat = adj_mat ) # (1, 128, 512)

Sie können das Netzwerk auch automatisch die Nachbarn N-ten Grades mit einem zusätzlichen Schlüsselwort num_adj_degrees ableiten lassen. Wenn Sie möchten, dass das System den Grad der Nachbarn als Kanteninformationen unterscheidet, übergeben Sie außerdem einen adj_dim ungleich Null.

 import torch
from se3_transformer_pytorch . se3_transformer_pytorch import SE3Transformer

model = SE3Transformer (
    dim = 64 ,
    depth = 1 ,
    attend_self = True ,
    num_degrees = 2 ,
    output_degrees = 2 ,
    num_neighbors = 0 ,
    attend_sparse_neighbors = True ,
    num_adj_degrees = 2 ,    # automatically derive 2nd degree neighbors
    adj_dim = 4             # embed 1st and 2nd degree neighbors (as well as null neighbors) with edge embeddings of this dimension
)

feats = torch . randn ( 1 , 32 , 64 )
coors = torch . randn ( 1 , 32 , 3 )
mask  = torch . ones ( 1 , 32 ). bool ()

# placeholder adjacency matrix
# naively assuming the sequence is one long chain (128, 128)

i = torch . arange ( 128 )
adj_mat = ( i [:, None ] <= ( i [ None , :] + 1 )) & ( i [:, None ] >= ( i [ None , :] - 1 ))

out = model ( feats , coors , mask , adj_mat = adj_mat , return_type = 1 )

Um eine genaue Kontrolle über die Dimensionalität jedes Typs zu haben, können Sie die Schlüsselwörter hidden_fiber_dict und out_fiber_dict verwenden, um ein Wörterbuch mit dem Grad an Dimensionswerte als Schlüssel/Werte zu übergeben.

 import torch
from se3_transformer_pytorch import SE3Transformer

model = SE3Transformer (
    num_tokens = 28 ,
    dim = 64 ,
    num_edge_tokens = 4 ,
    edge_dim = 16 ,
    depth = 2 ,
    input_degrees = 1 ,
    num_degrees = 3 ,
    output_degrees = 1 ,
    hidden_fiber_dict = { 0 : 16 , 1 : 8 , 2 : 4 },
    out_fiber_dict = { 0 : 16 , 1 : 1 },
    reduce_dim_out = False
)

atoms = torch . randint ( 0 , 28 , ( 2 , 32 ))
bonds = torch . randint ( 0 , 4 , ( 2 , 32 , 32 ))
coors = torch . randn ( 2 , 32 , 3 )
mask  = torch . ones ( 2 , 32 ). bool ()

pred = model ( atoms , coors , mask , edges = bonds )

pred [ '0' ] # (2, 32, 16)
pred [ '1' ] # (2, 32, 1, 3) 

Nachbarn

Sie können weiter steuern, welche Knoten berücksichtigt werden können, indem Sie eine Nachbarmaske übergeben. Alle False Werte werden aus Gründen der Berücksichtigung maskiert.

 import torch
from se3_transformer_pytorch . se3_transformer_pytorch import SE3Transformer

model = SE3Transformer (
    dim = 16 ,
    dim_head = 16 ,
    attend_self = True ,
    num_degrees = 4 ,
    output_degrees = 2 ,
    num_edge_tokens = 4 ,
    num_neighbors = 8 ,      # make sure you set this value as the maximum number of neighbors set by your neighbor_mask, or it will throw a warning
    edge_dim = 2 ,
    depth = 3
)

feats = torch . randn ( 1 , 32 , 16 )
coors = torch . randn ( 1 , 32 , 3 )
mask  = torch . ones ( 1 , 32 ). bool ()
bonds = torch . randint ( 0 , 4 , ( 1 , 32 , 32 ))

neighbor_mask = torch . ones ( 1 , 32 , 32 ). bool () # set the nodes you wish to be masked out as False

out = model (
    feats ,
    coors ,
    mask ,
    edges = bonds ,
    neighbor_mask = neighbor_mask ,
    return_type = 1
)

Globale Knoten

Mit dieser Funktion können Sie Vektoren übergeben, die als globale Knoten angesehen werden können, die von allen anderen Knoten gesehen werden. Die Idee wäre, Ihr Diagramm in ein paar Merkmalsvektoren zusammenzufassen, die auf alle Aufmerksamkeitsebenen im Netzwerk auf Schlüssel/Werte projiziert werden. Alle Knoten haben uneingeschränkten Zugriff auf globale Knoteninformationen, unabhängig von den nächsten Nachbarn oder der Adjazenzberechnung.

 import torch
from torch import nn
from se3_transformer_pytorch import SE3Transformer

model = SE3Transformer (
    dim = 64 ,
    depth = 1 ,
    num_degrees = 2 ,
    num_neighbors = 4 ,
    valid_radius = 10 ,
    global_feats_dim = 32 # this must be set to the dimension of the global features, in this example, 32
)

feats = torch . randn ( 1 , 32 , 64 )
coors = torch . randn ( 1 , 32 , 3 )
mask  = torch . ones ( 1 , 32 ). bool ()

# naively derive global features
# by pooling features and projecting
global_feats = nn . Linear ( 64 , 32 )( feats . mean ( dim = 1 , keepdim = True )) # (1, 1, 32)

out = model ( feats , coors , mask , return_type = 0 , global_feats = global_feats )

Todo:

• Ermöglichen Sie globalen Knoten, sich um alle anderen Knoten zu kümmern, um dem Netzwerk einen globalen Kanal für Informationen zu geben. (Ähnlich wie BigBird, ETC, Longformer usw.)

Autoregressiv

Sie können SE3 Transformers autoregressiv mit nur einem zusätzlichen Flag verwenden

 import torch
from se3_transformer_pytorch import SE3Transformer

model = SE3Transformer (
    dim = 512 ,
    heads = 8 ,
    depth = 6 ,
    dim_head = 64 ,
    num_degrees = 4 ,
    valid_radius = 10 ,
    causal = True          # set this to True
)

feats = torch . randn ( 1 , 1024 , 512 )
coors = torch . randn ( 1 , 1024 , 3 )
mask  = torch . ones ( 1 , 1024 ). bool ()

out = model ( feats , coors , mask ) # (1, 1024, 512) 

Experimentelle Funktionen

Nicht paarweise gefaltete Schlüssel

Ich habe herausgefunden, dass die Verwendung linear projizierter Schlüssel (anstelle der paarweisen Faltung) bei einer Spielzeug-Rauschunterdrückungsaufgabe in Ordnung zu sein scheint. Dies führt zu einer Speichereinsparung von 25 %. Sie können diese Funktion ausprobieren, indem Sie linear_proj_keys = True festlegen

 import torch
from se3_transformer_pytorch import SE3Transformer

model = SE3Transformer (
    dim = 64 ,
    depth = 1 ,
    num_degrees = 4 ,
    num_neighbors = 8 ,
    valid_radius = 10 ,
    splits = 4 ,
    linear_proj_keys = True # set this to True
). cuda ()

feats = torch . randn ( 1 , 32 , 64 ). cuda ()
coors = torch . randn ( 1 , 32 , 3 ). cuda ()
mask  = torch . ones ( 1 , 32 ). bool (). cuda ()

out = model ( feats , coors , mask , return_type = 0 )

Gemeinsamer Schlüssel/Werte über alle Köpfe hinweg

Es gibt eine relativ unbekannte Technik für Transformatoren, bei der man einen Schlüssel-/Wertkopf für alle Köpfe der Abfragen gemeinsam nutzen kann. Nach meiner Erfahrung mit NLP führt dies normalerweise zu einer schlechteren Leistung, aber wenn Sie wirklich auf Gedächtnisverlust für mehr Tiefe oder eine höhere Anzahl von Graden verzichten müssen, kann dies eine gute Option sein.

 import torch
from se3_transformer_pytorch import SE3Transformer

model = SE3Transformer (
    dim = 64 ,
    depth = 8 ,
    num_degrees = 4 ,
    num_neighbors = 8 ,
    valid_radius = 10 ,
    splits = 4 ,
    one_headed_key_values = True  # one head of key / values shared across all heads of the queries
). cuda ()

feats = torch . randn ( 1 , 32 , 64 ). cuda ()
coors = torch . randn ( 1 , 32 , 3 ). cuda ()
mask  = torch . ones ( 1 , 32 ). bool (). cuda ()

out = model ( feats , coors , mask , return_type = 0 )

Gebundener Schlüssel/Werte

Sie können die Schlüssel/Werte auch verknüpfen (sie müssen gleich sein), um die Hälfte des Speichers zu sparen

 import torch
from se3_transformer_pytorch import SE3Transformer

model = SE3Transformer (
    dim = 64 ,
    depth = 8 ,
    num_degrees = 4 ,
    num_neighbors = 8 ,
    valid_radius = 10 ,
    splits = 4 ,
    tie_key_values = True # set this to True
). cuda ()

feats = torch . randn ( 1 , 32 , 64 ). cuda ()
coors = torch . randn ( 1 , 32 , 3 ). cuda ()
mask  = torch . ones ( 1 , 32 ). bool (). cuda ()

out = model ( feats , coors , mask , return_type = 0 )

Verwendung von EGNN

Dies ist eine experimentelle Version von EGNN, die für höhere Typen und eine größere Dimensionalität als nur 1 (für die Koordinaten) funktioniert. Der Klassenname lautet immer noch SE3Transformer , da er bereits vorhandene Logik wiederverwendet. Ignorieren Sie ihn also vorerst, bis ich ihn später bereinige.

 import torch
from se3_transformer_pytorch import SE3Transformer

model = SE3Transformer (
    dim = 32 ,
    num_neighbors = 8 ,
    num_edge_tokens = 4 ,
    edge_dim = 4 ,
    num_degrees = 4 ,       # number of higher order types - will use basis on a TCN to project to these dimensions
    use_egnn = True ,       # set this to true to use EGNN instead of equivariant attention layers
    egnn_hidden_dim = 64 ,  # egnn hidden dimension
    depth = 4 ,             # depth of EGNN
    reduce_dim_out = True  # will project the dimension of the higher types to 1
). cuda ()

feats = torch . randn ( 2 , 32 , 32 ). cuda ()
coors = torch . randn ( 2 , 32 , 3 ). cuda ()
bonds = torch . randint ( 0 , 4 , ( 2 , 32 , 32 )). cuda ()
mask  = torch . ones ( 2 , 32 ). bool (). cuda ()

refinement = model ( feats , coors , mask , edges = bonds , return_type = 1 ) # (2, 32, 3)

coors = coors + refinement  # update coors with refinement

Wenn Sie für jeden der höheren Typen individuelle Dimensionen angeben möchten, übergeben Sie einfach hidden_fiber_dict , wobei das Wörterbuch im Format {<degree>:<dim>} anstelle von num_degrees vorliegt

 import torch
from se3_transformer_pytorch import SE3Transformer

model = SE3Transformer (
    dim = 32 ,
    num_neighbors = 8 ,
    hidden_fiber_dict = { 0 : 32 , 1 : 16 , 2 : 8 , 3 : 4 },
    use_egnn = True ,
    depth = 4 ,
    egnn_hidden_dim = 64 ,
    egnn_weights_clamp_value = 2 , 
    reduce_dim_out = True
). cuda ()

feats = torch . randn ( 2 , 32 , 32 ). cuda ()
coors = torch . randn ( 2 , 32 , 3 ). cuda ()
mask  = torch . ones ( 2 , 32 ). bool (). cuda ()

refinement = model ( feats , coors , mask , return_type = 1 ) # (2, 32, 3)

coors = coors + refinement  # update coors with refinement 

Skalierung (Wip)

In diesem Abschnitt werden die laufenden Bemühungen aufgeführt, die Skalierung von SE3 Transformer etwas zu verbessern.

Erstens habe ich reversible Netzwerke hinzugefügt. Dadurch kann ich etwas mehr Tiefe hinzufügen, bevor ich auf die üblichen Speicherhindernisse stoße. In den Tests wird der Erhalt der Äquivarianz nachgewiesen.

 import torch
from se3_transformer_pytorch import SE3Transformer

model = SE3Transformer (
    num_tokens = 20 ,
    dim = 32 ,
    dim_head = 32 ,
    heads = 4 ,
    depth = 12 ,             # 12 layers
    input_degrees = 1 ,
    num_degrees = 3 ,
    output_degrees = 1 ,
    reduce_dim_out = True ,
    reversible = True       # set reversible to True
). cuda ()

atoms = torch . randint ( 0 , 4 , ( 2 , 32 )). cuda ()
coors = torch . randn ( 2 , 32 , 3 ). cuda ()
mask  = torch . ones ( 2 , 32 ). bool (). cuda ()

pred = model ( atoms , coors , mask = mask , return_type = 0 )

loss = pred . sum ()
loss . backward ()

Beispiele

Installieren Sie zuerst sidechainnet

$ pip install sidechainnet

Führen Sie dann die Aufgabe zur Rauschunterdrückung des Protein-Backbones aus

$ python denoise.py

Caching

Standardmäßig werden die Basisvektoren zwischengespeichert. Sollte jedoch jemals die Notwendigkeit bestehen, den Cache zu leeren, müssen Sie beim Starten des Skripts lediglich das Umgebungsflag CLEAR_CACHE auf einen bestimmten Wert setzen

$ CLEAR_CACHE=1 python train.py

Oder Sie können versuchen, das Cache-Verzeichnis zu löschen, das unter vorhanden sein sollte

$ rm -rf ~ /.cache.equivariant_attention

Sie können auch Ihr eigenes Verzeichnis festlegen, in dem die Caches gespeichert werden sollen, falls im Standardverzeichnis möglicherweise Berechtigungsprobleme bestehen

CACHE_PATH=./path/to/my/cache python train.py

Testen

$ python setup.py pytest

Kredit

Diese Bibliothek ist größtenteils eine Portierung von Fabians offiziellem Repository, jedoch ohne die DGL-Bibliothek.

Zitate

 @misc { fuchs2020se3transformers ,
    title   = { SE(3)-Transformers: 3D Roto-Translation Equivariant Attention Networks } , 
    author  = { Fabian B. Fuchs and Daniel E. Worrall and Volker Fischer and Max Welling } ,
    year    = { 2020 } ,
    eprint  = { 2006.10503 } ,
    archivePrefix = { arXiv } ,
    primaryClass = { cs.LG }
}

 @misc { satorras2021en ,
    title   = { E(n) Equivariant Graph Neural Networks } ,
    author  = { Victor Garcia Satorras and Emiel Hoogeboom and Max Welling } ,
    year    = { 2021 } ,
    eprint  = { 2102.09844 } ,
    archivePrefix = { arXiv } ,
    primaryClass = { cs.LG }
}

 @misc { gomez2017reversible ,
    title     = { The Reversible Residual Network: Backpropagation Without Storing Activations } ,
    author    = { Aidan N. Gomez and Mengye Ren and Raquel Urtasun and Roger B. Grosse } ,
    year      = { 2017 } ,
    eprint    = { 1707.04585 } ,
    archivePrefix = { arXiv } ,
    primaryClass = { cs.CV }
}

 @misc { shazeer2019fast ,
    title   = { Fast Transformer Decoding: One Write-Head is All You Need } ,
    author  = { Noam Shazeer } ,
    year    = { 2019 } ,
    eprint  = { 1911.02150 } ,
    archivePrefix = { arXiv } ,
    primaryClass = { cs.NE }
}