
Der Team -Moderator: Kahraman Kostas
Um Ihnen den Einstieg zu erleichtern, haben wir ein einfaches Problem zusammengestellt, um einige wichtige Innenpositionierungskonzepte einzuführen. Betrachten Sie die folgende Umgebung: Ein Benutzer reist in Vorhandensein 3 WLAN -Emitter im offenen Raum (wir nennen die von diesem Benutzer erstellten Daten eine Flugbahn). Jeder Emitter hat eine eindeutige MAC -Adresse. Der Benutzer ist mit einem Smartphone ausgestattet, das regelmäßig die WLAN -Umgebung scannt und die RSSI jedes erkannten Mac (in DB) aufzeichnet.
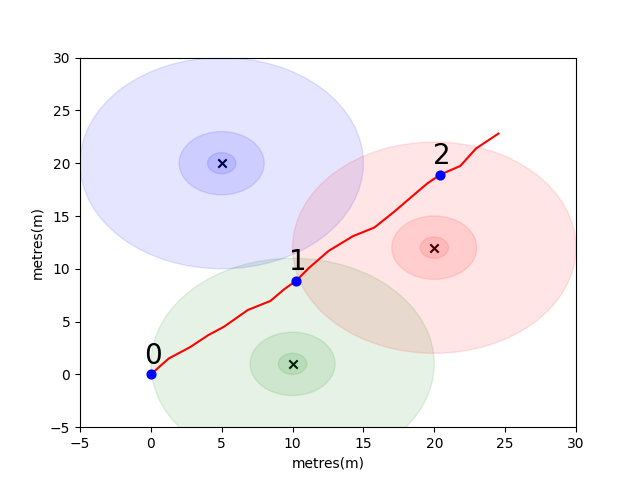
Für dieses Modell haben wir für jeden der Emitter ein Standardmodell für protokontrische Log-Loss-Freiraum verwendet. Dies ist ein simpeltes Modell, das im freien Raum gut funktioniert, aber in realen Innenumgebungen mit Wänden und anderen Hindernissen zusammenbricht, die die Signale auf komplexere Weise abprallen können. Im Allgemeinen erwarten wir einen steilen Rückgang von RSSI über die Entfernung, da die feste Energie aus der emittierenden Antenne über einen zunehmenden Bereich ausbreitet, wenn sich die Welle ausbreitet. Im Diagramm unter jedem Kreis bezeichnet ein Tropfen von 10 dB.
Der Benutzer geht von Punkt (0,0) nach Nordosten und dort telefoniert drei Scans der Umgebung. Die bei jedem Scan aufgezeichneten Daten sind unten angezeigt.
scan 0 -> {'green': -60, 'blue': -66, 'red': -67}
scan 1 -> {'green': -58, 'blue': -61, 'red': -60}
scan 2 -> {'green': -66, 'blue': -62, 'red': -59}
Die komplexen und lokal einzigartigen Eigenschaften der WLAN -Umgebung machen es für Innenpositionierungssysteme sehr nützlich. Zum Beispiel misst im folgenden Bild scan 1 Daten in ungefähr dem Schwerpunkt der drei Emitter, und es gibt keinen anderen Ort in dieser Umgebung, in dem man eine Lesung einnehmen könnte, die ähnliche RSSI -Werte registrieren würde. Angesichts einer Reihe von Scans oder "Fingerabdrücken" aus unabhängigen Trajektorien möchten wir berechnen, wie ähnlich sie im WLAN -Raum sind, da dies ein Hinweis darauf ist, wie nahe sie im realen Raum sind.
Ihre erste Herausforderung besteht darin, eine Funktion zur Berechnung der euklidischen Distanz- und Manhattan -Distanzmetriken zwischen den beiden oben eingeführten Scans in der von uns eingeführten Stichprobenentfernung zu schreiben. Die Verwendung der Daten aus einer einzelnen Flugbahn ist eine gute Möglichkeit, die Qualität einer Ähnlichkeitsmetrik zu testen, da wir mit den Daten aus der Gezeitenmesseinheit des Telefons (IMU), die von einer fußgängeren Toten -Abrechnung verwendet werden, ziemlich genaue Schätzungen der tatsächlichen Entfernung erhalten können. (PDR) Modul.
def euclidean ( fp1 , fp2 ):
raise NotImplementedError
def manhattan ( fp1 , fp2 ):
raise NotImplementedError # solution of the above functions
from scipy . spatial import distance
def euclidean ( fp1 , fp2 ):
fp1 = list ( fp1 . values ())
fp2 = list ( fp2 . values ())
return distance . euclidean ( fp1 , fp2 )
def manhattan ( fp1 , fp2 ):
fp1 = list ( fp1 . values ())
fp2 = list ( fp2 . values ())
return distance . cityblock ( fp1 , fp2 ) import json
import numpy as np
import matplotlib . pyplot as plt
from metrics import eval_dist_metric
with open ( "intro_trajectory_1.json" ) as f :
traj = json . load ( f )
## Pre-calculate the pair indexes we are interested in
keys = []
for fp1 in traj [ 'fps' ]:
for fp2 in traj [ 'fps' ]:
# only calculate the upper triangle
if fp1 [ 'step_index' ] > fp2 [ 'step_index' ]:
keys . append (( fp1 [ 'step_index' ], fp2 [ 'step_index' ]))
## Get the distances from PDR
true_d = {}
for step1 in traj [ 'steps' ]:
for step2 in traj [ 'steps' ]:
key = ( step1 [ 'step_index' ], step2 [ 'step_index' ])
if key in keys :
true_d [ key ] = abs ( step1 [ 'di' ] - step2 [ 'di' ])
euc_d = {}
man_d = {}
for fp1 in traj [ 'fps' ]:
for fp2 in traj [ 'fps' ]:
key = ( fp1 [ 'step_index' ], fp2 [ 'step_index' ])
if key in keys :
euc_d [ key ] = euclidean ( fp1 [ 'profile' ], fp2 [ 'profile' ])
man_d [ key ] = manhattan ( fp1 [ 'profile' ], fp2 [ 'profile' ])
print ( "Euclidean Average Error" )
print ( f' { eval_dist_metric ( euc_d , true_d ):.2f } ' )
print ( "Manhattan Average Error" )
print ( f' { eval_dist_metric ( man_d , true_d ):.2f } ' ) Euclidean Average Error
9.29
Manhattan Average Error
4.90
Wenn Sie die Funktionen korrekt implementiert haben, sollten Sie feststellen, dass der durchschnittliche Fehler für die euklidische Metrik 9.29 betrug, während der Manhattan nur 4.90 betrug. Für diese Daten ist die Distanz von Manhattan eine bessere Schätzung der wahren Entfernung.
Dies ist natürlich ein sehr simple Modell. In der Tat gibt es auf diese Weise keine direkte Beziehung zwischen den RSSI -Werten und der freien Raumstrecke. Wenn wir unsere eigenen Schätzungen für die Entfernung erstellen, würden wir die bekannten PDR -Entfernungen innerhalb einer Flugbahn so verwenden, um die numerische Punktzahl in eine physische Entfernungsschätzung anzupassen.
Für Ihre Hauptherausforderung möchten wir, dass Sie Ihre eigene Metrik entwickeln, um die reale Distanz zwischen zwei Scans abzuschätzen, die ausschließlich auf ihren WLAN-Fingerabdrücken basieren. Wir werden Ihnen echte Crowdsourced -Daten zur Verfügung stellen, die Anfang 2021 aus einem einzigen Einkaufszentrum gesammelt wurden. Die Daten enthalten 114661 Fingerabdrücke Scans und 879824 Entfernungen zwischen den Scans. Die Entfernungen sind unsere beste Schätzung der tatsächlichen Entfernung bei zusätzlichen Informationen, die wir berücksichtigen werden.
Wir werden einen Testsatz von Fingerabdruckpaaren bereitstellen und Sie müssen eine Funktion schreiben, die uns sagt, wie weit sie sind.
Diese Funktion könnte so einfach sein wie eine Variation einer der oben eingeführten Metriken oder so komplex wie eine vollständige maschinelle Lernlösung, die in verschiedenen Situationen unterschiedlich lernt, verschiedene MAC -Adressen (oder MAC -Adresskombinationen) unterschiedlich zu gewichten.
Einige letzte Punkte zu berücksichtigen:
Die Daten werden als drei Dateien für Sie zusammengestellt.
Die task1_fingerprints.json enthält alle Fingerabdruckinformationen für das Problem. Das ist, dass jeder Eintrag einen echten Scan der WLAN -Emitter in einem Bereich des Einkaufszentrums darstellt. Sie werden feststellen, dass in vielen Fingerabdrücken dieselben MAC -Adressen vorhanden sein werden.
Der task1_train.csv enthält die gültigen Trainingspaare, mit denen Sie Ihren Algorithmus entwerfen/trainieren können. Jedes id1-id2 -Paar hat eine markierte Bodenwahrheitsabstand (in Metern) und jede ID entspricht Fingerabdrücken von task1_fingerprints.json .
Das task1_test.csv ist das gleiche Format wie task1_train.csv verfügt jedoch nicht über die Verschiebungen. Dies sind das, was wir vorhersagen möchten, dass Sie die Informationen über die Rohfingerabdruckinformationen verwenden.
import csv
import json
import os
from tqdm import tqdm
path_to_data = "for_contestants"
with open ( os . path . join ( path_to_data , "task1_fingerprints.json" )) as f :
fps = json . load ( f )
with open ( os . path . join ( path_to_data , "task1_train.csv" )) as f :
train_data = []
train_h = csv . DictReader ( f )
for pair in tqdm ( train_h ):
train_data . append ([ pair [ 'id1' ], pair [ 'id2' ], float ( pair [ 'displacement' ])])
with open ( os . path . join ( path_to_data , "task1_test.csv" )) as f :
test_h = csv . DictReader ( f )
test_ids = []
for pair in tqdm ( test_h ):
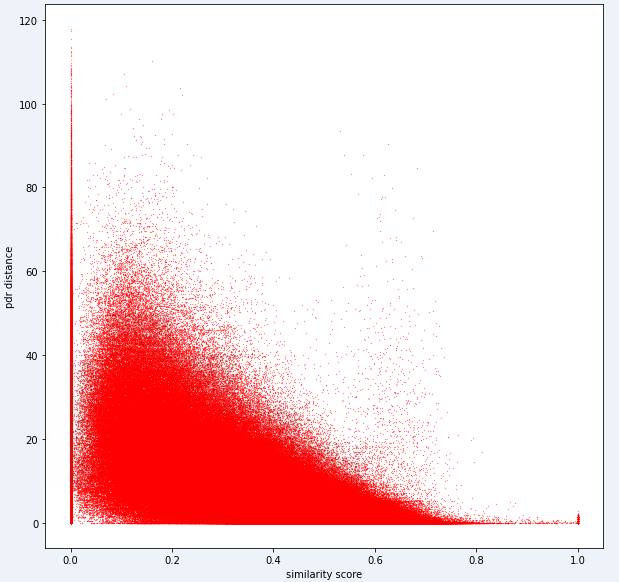
test_ids . append ([ pair [ 'id1' ], pair [ 'id2' ]])Letztendlich sollte das ideale Modell in der Lage sein, eine exakte Zuordnung zwischen dem hochdimensionalen Fingerabdruckraum (1 Fingerabdruck kann viele Messungen enthalten) und dem 1 -dimensionalen Abstandsraum zu finden. Es kann nützlich sein, die PDR -Distanz (aus den Trainingsdaten) gegen eine berechnete Ähnlichkeitsmetrik zu zeichnen, um festzustellen, ob die Metrik einen offensichtlichen Trend zeigt. Eine hohe Ähnlichkeit sollte mit einem geringen Abstand korrelieren.
Unten finden Sie eine Entfernungsmetrik, die wir für diese Aufgabe intern verwenden. Sie können sehen, dass wir selbst für diese Metrik eine beträchtliche Menge an Lärm haben.
Aufgrund dieses Rauschens wird unsere Bewertungsmetrik für Aufgabe 1 in Richtung Präzision gegenüber dem Rückruf voreingenommen
Ihre Einreichung sollte die genauen IDs aus der Datei test1_test.csv verwenden und die dritte (derzeit leere) Verschiebungsspalte mit Ihrer geschätzten Entfernung (in Messgeräten) für dieses Fingerabdruckpaar füllen.
def my_distance_function ( fp1 , fp2 ):
raise NotImplementedError output_data = [[ "id1" , "id2" , "displacement" ]]
for id1 , id2 in tqdm ( test_ids ):
fp1 = fps [ id1 ]
fp2 = fps [ id2 ]
distance_estimate = my_distance_function ( fp1 , fp2 )
output_data . append ([ id1 , id2 , distance_estimate ])
with open ( "MySubmission.csv" , "w" , newline = '' ) as f :
writer = csv . writer ( f )
writer . writerows ( output_data )Die Schritte in der ersten Aufgabe können wie folgt zusammengefasst werden.
Diese Schritte sind im Bild unten dargestellt.

Wir haben Python 3.6.5 verwendet, um die Anwendungsdatei zu erstellen. Wir haben einige zusätzliche Module aufgenommen, die zu Beginn des Wettbewerbs nicht in die Beispieldatei enthalten waren. Diese Module können als:
| Molules | Aufgabe |
|---|---|
| Tensorflow | Tiefes Lernen |
| Pandas | Datenanalyse |
| Scipy | Entfernungscomputer |
Wir begannen mit der Installation dieser Module als erster Schritt.
## 1.1 Installing modules
!p ip install tensorflow == 2.6 . 2
!p ip install scipy
!p ip install pandas In diesem Schritt haben wir den zu verwendeten zufälligen Saatgut festgelegt, um wiederholbare Ergebnisse zu erzielen. Auf diese Weise haben wir einen deterministischen Weg geliefert, auf dem wir in jedem Lauf dasselbe Ergebnis erzielen. Nach unseren Beobachtungen können die mit unterschiedlichen Computer erhaltenen Ergebnisse jedoch geringfügig unterscheiden (± 1%)
## 1.2 Setting Random Seeds
seed_value = 0
import os
os . environ [ 'PYTHONHASHSEED' ] = str ( seed_value )
import random
random . seed ( seed_value )
import numpy as np
np . random . seed ( seed_value )
import tensorflow as tf
tf . random . set_seed ( seed_value )
import tensorflow as tf
session_conf = tf . compat . v1 . ConfigProto ( intra_op_parallelism_threads = 1 , inter_op_parallelism_threads = 1 )
sess = tf . compat . v1 . Session ( graph = tf . compat . v1 . get_default_graph (), config = session_conf ) In diesem Abschnitt laden wir die von uns verwendeten Daten. Wir haben den Code und die Erläuterungen aus der angegebenen Beispieldatei ( Task1-IPS-Challenge-2021.ipynb ) genommen.
Die task1_fingerprints.json enthält alle Fingerabdruckinformationen für das Problem. Das ist, dass jeder Eintrag einen echten Scan der WLAN -Emitter in einem Bereich des Einkaufszentrums darstellt. Sie werden feststellen, dass in vielen Fingerabdrücken dieselben MAC -Adressen vorhanden sein werden.
Der task1_train.csv enthält die gültigen Trainingspaare, mit denen Sie Ihren Algorithmus entwerfen/trainieren können. Jedes id1-id2 -Paar hat eine markierte Bodenwahrheitsabstand (in Metern) und jede ID entspricht Fingerabdrücken von task1_fingerprints.json .
Das task1_test.csv ist das gleiche Format wie task1_train.csv verfügt jedoch nicht über die Verschiebungen.
## 1.3 Loading the data
import csv
import json
import os
from tqdm import tqdm
path_to_data = "for_contestants"
with open ( os . path . join ( path_to_data , "task1_fingerprints.json" )) as f :
fps = json . load ( f )
with open ( os . path . join ( path_to_data , "task1_train.csv" )) as f :
train_data = []
train_h = csv . DictReader ( f )
for pair in tqdm ( train_h ):
train_data . append ([ pair [ 'id1' ], pair [ 'id2' ], float ( pair [ 'displacement' ])])
with open ( os . path . join ( path_to_data , "task1_test.csv" )) as f :
test_h = csv . DictReader ( f )
test_ids = []
for pair in tqdm ( test_h ):
test_ids . append ([ pair [ 'id1' ], pair [ 'id2' ]]) 879824it [05:16, 2778.31it/s]
5160445it [01:00, 85269.27it/s]
In diesem Schritt führen wir die Feature -Extraktion mit zwei Funktionen durch. Die Funktion feature_extraction_file zieht einfach die relevanten Werte der Fingerabdrücke (paarweise) aus der JSON -Datei und sendet sie an die Funktion feature_extraction , um die Berechnungen durchzuführen.
In der Funktion feature_extraction , wenn sich diese beiden Fingerabdrücke in Bezug auf die Größe und die von ihnen enthaltenen Geräte unterscheiden, werden alle in den beiden Fingerabdrücken enthaltenen Geräte zusammengeführt, um eine gemeinsame Sequenz zu bilden, ohne sich wieder zu wiederholen. In jedem Array machen wir diese beiden Arrays identisch (in Bezug auf Geräte, die sie einschließen) identisch, indem wir den Wert 0 den nicht korrekten Geräten zuweisen. Dieser Prozess wird mit einem Beispiel im folgenden Bild erklärt.
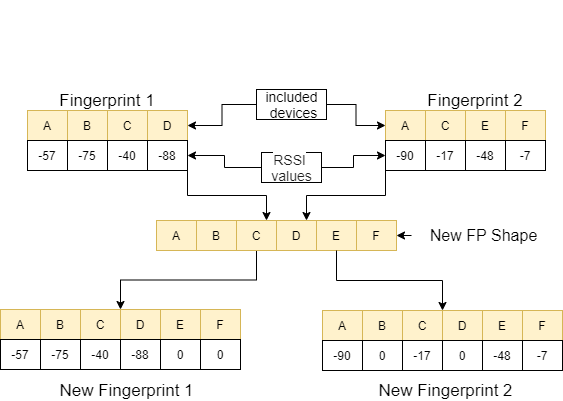
Der Abstand zwischen diesen beiden ähnlichen Fingerabdrücken wird unter Verwendung von 11 verschiedenen Methoden berechnet [1]. Diese Methoden sind:
Anschließend werden diese Werte in die Funktion feature_extraction_file gerichtet und als CSV -Datei in dieser Funktion gespeichert. Mit anderen Worten, Fingerabdrücke verschiedener Größen verwandeln sich infolge dieses Prozesses in eine CSV-Datei mit 11 Featuren. Das zu verwendende Modell wird mit diesen neu erstellten Funktionen trainiert und getestet.
## 1.4 Feature Extraction
def feature_extraction_file ( data , name , flag ):
features = [[ "braycurtis" ,
"canberra" ,
"chebyshev" ,
"cityblock" ,
"correlation" ,
"cosine" ,
"euclidean" ,
"jensenshannon" ,
"minkowski" ,
"sqeuclidean" ,
"wminkowski" , "real" ]]
for i in tqdm (( data ), position = 0 , leave = True ):
fp1 = fps [ i [ 0 ]]
fp2 = fps [ i [ 1 ]]
feature = feature_extraction ( fp1 , fp2 )
if flag :
feature . append ( i [ 2 ])
else : feature . append ( 0 )
features . append ( feature )
with open ( name , "w" , newline = '' ) as f :
writer = csv . writer ( f )
writer . writerows ( features )
#print(features) ## 1.4 Feature Extraction
def feature_extraction ( fp1 , fp2 ):
mac = set ( list ( fp1 . keys ()) + list ( fp2 . keys ()))
mac = { i : 0 for i in mac }
f1 = mac . copy ()
f2 = mac . copy ()
for key in fp1 :
f1 [ key ] = fp1 [ key ]
for key in fp2 :
f2 [ key ] = fp2 [ key ]
f1 = list ( f1 . values ())
f2 = list ( f2 . values ())
braycurtis = scipy . spatial . distance . braycurtis ( f1 , f2 )
canberra = scipy . spatial . distance . canberra ( f1 , f2 )
chebyshev = scipy . spatial . distance . chebyshev ( f1 , f2 )
cityblock = scipy . spatial . distance . cityblock ( f1 , f2 )
correlation = scipy . spatial . distance . correlation ( f1 , f2 )
cosine = scipy . spatial . distance . cosine ( f1 , f2 )
euclidean = scipy . spatial . distance . euclidean ( f1 , f2 )
jensenshannon = scipy . spatial . distance . jensenshannon ( f1 , f2 )
minkowski = scipy . spatial . distance . minkowski ( f1 , f2 )
sqeuclidean = scipy . spatial . distance . sqeuclidean ( f1 , f2 )
wminkowski = scipy . spatial . distance . wminkowski ( f1 , f2 , 1 , np . ones ( len ( f1 )))
output_data = [ braycurtis ,
canberra ,
chebyshev ,
cityblock ,
correlation ,
cosine ,
euclidean ,
jensenshannon ,
minkowski ,
sqeuclidean ,
wminkowski ]
output_data = [ 0 if x != x else x for x in output_data ]
return output_data In dieser Aufgabe gibt es Fingerabdrücke Scans mit RRSI -Signalen von WiFi -Emitter -Umgebungen im Einkaufszentrum. First Challange möchte, dass wir den Abstand zwischen zwei Fingerabdrücken Scans schätzen, was eine Regressionsaufgabe ist. Wir haben Ann (künstliche neuronale Netzwerke) verwendet, die vom biologischen neuronalen Netzwerk inspiriert sind. Ann besteht aus drei Schichten; Eingangsschicht, versteckte Schichten (mehr als eine) und Ausgangsschicht. Ann beginnt mit Eingabeschicht, die die Trainingsdaten (mit Merkmalen) enthält, übergeben die Daten an die erste versteckte Ebene, in der die Daten durch die Gewichte der ersten versteckten Schicht berechnet werden. In versteckten Schichten gibt es eine Iteration der Berechnung von Gewichten auf die Eingänge und wenden sie dann eine Aktivierungsfunktion an [2]. Da unser Problem die Regression ist, ist unsere letzte Schicht ein einzelnes Ausgangsneuron: Die Ausgabe ist die vorhergesagte Entfernungen zwischen Paaren von Fingerabdruck -Scans. Unsere erste versteckte Schicht hat 64 und die zweite hat 128 Neuronen. Die alle Architektur dieses Modells wird wie folgt geteilt. 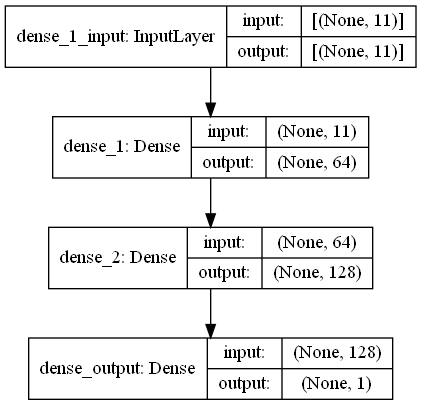
Wir führen Deep Learning unter Verwendung von zwei Funktionen durch. Die Funktion create_model formt die Trainingsdaten, um das Modell zu trainieren, und bestimmt die Struktur des Modells. Die Funktion model_features erzeugt ein Modell mit der angegebenen Struktur. Das erstellte Modell wird gespeichert, um nach der Schulung durch die Funktion create_model verwendet zu werden.
## 1.5 Model
import scipy . spatial
import pandas as pd
import numpy as np
import matplotlib . pyplot as plt
from tensorflow import keras
from tensorflow . keras . models import Sequential
from tensorflow . keras . layers import Dense
#from keras.utils.vis_utils import plot_model
% matplotlib inline
def model_features ( i , ii ):
model = Sequential ()
model . add ( Dense ( i , input_shape = ( 11 , ), activation = 'relu' , name = 'dense_1' ))
model . add ( Dense ( ii , activation = 'relu' , name = 'dense_2' ))
model . add ( Dense ( 1 , activation = 'linear' , name = 'dense_output' ))
model . compile ( optimizer = 'adam' , loss = 'mse' , metrics = [ 'mae' ])
model . summary ()
#plot_model(model, to_file='model_plot.png', show_shapes=True, show_layer_names=True)
#print(model.get_config())
return model
def create_model ( name ):
df = pd . read_csv ( name )
df . replace ([ np . inf , - np . inf ], np . nan , inplace = True )
df = df . fillna ( 0 )
X = df [ df . columns [ 0 : - 1 ]]
X_train = np . array ( X )
y_train = np . array ( df [ df . columns [ - 1 ]])
model = model_features ( 64 , 128 )
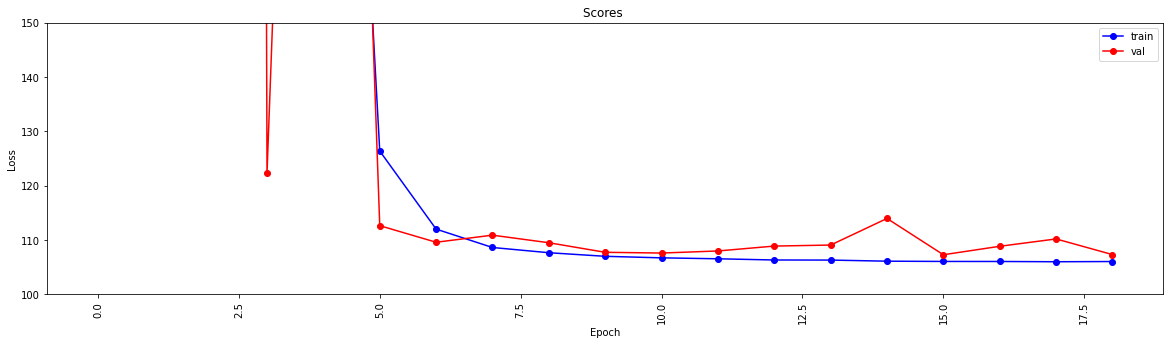
history = model . fit ( X_train , y_train , epochs = 19 , validation_split = 0.5 ) #,batch_size=1)
loss = history . history [ 'loss' ]
val_loss = history . history [ 'val_loss' ]
my_xticks = list ( range ( len ( loss )))
plt . figure ( figsize = ( 20 , 5 ))
plt . plot ( my_xticks , loss , linestyle = '-' , marker = 'o' , color = 'b' , label = "train" )
plt . plot ( my_xticks , val_loss , linestyle = '-' , marker = 'o' , color = 'r' , label = "val" )
plt . title ( "Scores " )
plt . legend ( numpoints = 1 )
plt . ylabel ( "Loss" )
plt . xlabel ( "Epoch" )
plt . xticks ( rotation = 90 )
plt . ylim ([ 100 , 150 ])
plt . show ()
madelname = "./THEMODEL"
model . save ( madelname )
print ( "Model Created!" )
Diese Funktion prüft, ob die Trainings- und Testdaten die Funktionextraktion durchlaufen haben. Wenn dies nicht der Fall ist, wird diese Dateien und das Modell erstellt, indem die entsprechenden Funktionen aufgerufen werden. Nach dem Umgang mit dem Modell und der gesamten Merkmalextraktion formatiert es die Testdaten, um die endgültigen Ergebnisse zu erzielen.
## 1.6 Checking the inputs
from numpy import inf
from numpy import nan
def create_new_files ( train , test ):
model_path = "./THEMODEL/"
my_train_file = 'new_train_features.csv'
my_test_file = 'new_test_features.csv'
if os . path . isfile ( my_train_file ) :
pass
else :
print ( "Please wait! Training data feature extraction is in progress... n it will take about 10 minutes" )
feature_extraction_file ( train , my_train_file , 1 )
print ( "TThe training feature extraction completed!!!" )
if os . path . isfile ( my_test_file ) :
pass
else :
print ( "Please wait! Testing data feature extraction is in progress... n it will take about 100-120 minutes" )
feature_extraction_file ( test , my_test_file , 0 )
print ( "The testing feature extraction completed!!!" )
if os . path . isdir ( model_path ):
pass
else :
print ( "Please wait! Creating the deep learning model... n it will take about 10 minutes" )
create_model ( my_train_file )
print ( "The model file created!!! n n n " )
model = keras . models . load_model ( model_path )
df = pd . read_csv ( my_test_file )
df . replace ([ np . inf , - np . inf ], np . nan , inplace = True )
df = df . fillna ( 0 )
X_train = df [ df . columns [ 0 : - 1 ]]
X_train = np . array ( X_train )
y_train = np . array ( df [ df . columns [ - 1 ]])
predicted = model . predict ( X_train )
print ( "Please wait! Creating resuşts... " )
return predicted Dieser Schritt löst die Feature -Extraktion und die Modellerstellungsprozesse aus und ermöglicht es allen Prozessen. Mit den IDs aus der Datei test1_test.csv wird die dritte (Verschiebung) Spalte mit der geschätzten Entfernung für diese Fingerabdruckpaare gefüllt und diese Datei im Verzeichnis mit dem Namen TASK1-MySubmission.csv gespeichert.
## 1.7 Submission
distance_estimate = create_new_files ( train_data , test_ids )
count = 0
output_data = [[ "id1" , "id2" , "displacement" ]]
for id1 , id2 in tqdm ( test_ids ):
output_data . append ([ id1 , id2 , distance_estimate [ count ][ 0 ]])
count += 1
print ( "Process finished. Preparing result file ..." )
with open ( "TASK1-MySubmission.csv" , "w" , newline = '' ) as f :
writer = csv . writer ( f )
writer . writerows ( output_data )
print ( "The results are ready. n See MySubmission.csv" ) Please wait! Creating the deep learning model...
it will take about 10 minutes
Model: "sequential_3"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_1 (Dense) (None, 64) 768
_________________________________________________________________
dense_2 (Dense) (None, 128) 8320
_________________________________________________________________
dense_output (Dense) (None, 1) 129
=================================================================
Total params: 9,217
Trainable params: 9,217
Non-trainable params: 0
_________________________________________________________________
Epoch 1/19
13748/13748 [==============================] - 30s 2ms/step - loss: 2007233.6250 - mae: 161.3013 - val_loss: 218.8822 - val_mae: 11.5630
Epoch 2/19
13748/13748 [==============================] - 27s 2ms/step - loss: 24832.6309 - mae: 53.9385 - val_loss: 123437.0859 - val_mae: 307.2885
Epoch 3/19
13748/13748 [==============================] - 26s 2ms/step - loss: 4028.0859 - mae: 29.9960 - val_loss: 3329.2024 - val_mae: 49.9126
Epoch 4/19
13748/13748 [==============================] - 27s 2ms/step - loss: 904.7919 - mae: 17.6284 - val_loss: 122.3358 - val_mae: 6.8169
Epoch 5/19
13748/13748 [==============================] - 25s 2ms/step - loss: 315.7050 - mae: 11.9098 - val_loss: 404.0973 - val_mae: 15.2033
Epoch 6/19
13748/13748 [==============================] - 26s 2ms/step - loss: 126.3843 - mae: 7.8173 - val_loss: 112.6499 - val_mae: 7.6804
Epoch 7/19
13748/13748 [==============================] - 27s 2ms/step - loss: 112.0149 - mae: 7.4220 - val_loss: 109.5987 - val_mae: 7.1964
Epoch 8/19
13748/13748 [==============================] - 26s 2ms/step - loss: 108.6342 - mae: 7.3271 - val_loss: 110.9016 - val_mae: 7.6862
Epoch 9/19
13748/13748 [==============================] - 26s 2ms/step - loss: 107.6721 - mae: 7.2827 - val_loss: 109.5083 - val_mae: 7.5235
Epoch 10/19
13748/13748 [==============================] - 27s 2ms/step - loss: 107.0110 - mae: 7.2290 - val_loss: 107.7498 - val_mae: 7.1105
Epoch 11/19
13748/13748 [==============================] - 29s 2ms/step - loss: 106.7296 - mae: 7.2158 - val_loss: 107.6115 - val_mae: 7.1178
Epoch 12/19
13748/13748 [==============================] - 26s 2ms/step - loss: 106.5561 - mae: 7.2039 - val_loss: 107.9937 - val_mae: 6.9932
Epoch 13/19
13748/13748 [==============================] - 26s 2ms/step - loss: 106.3344 - mae: 7.1905 - val_loss: 108.8941 - val_mae: 7.4530
Epoch 14/19
13748/13748 [==============================] - 27s 2ms/step - loss: 106.3188 - mae: 7.1927 - val_loss: 109.0832 - val_mae: 7.5309
Epoch 15/19
13748/13748 [==============================] - 27s 2ms/step - loss: 106.1150 - mae: 7.1829 - val_loss: 113.9741 - val_mae: 7.9496
Epoch 16/19
13748/13748 [==============================] - 26s 2ms/step - loss: 106.0676 - mae: 7.1788 - val_loss: 107.2984 - val_mae: 7.2192
Epoch 17/19
13748/13748 [==============================] - 27s 2ms/step - loss: 106.0614 - mae: 7.1733 - val_loss: 108.8553 - val_mae: 7.4640
Epoch 18/19
13748/13748 [==============================] - 28s 2ms/step - loss: 106.0113 - mae: 7.1790 - val_loss: 110.2068 - val_mae: 7.6562
Epoch 19/19
13748/13748 [==============================] - 27s 2ms/step - loss: 106.0519 - mae: 7.1791 - val_loss: 107.3276 - val_mae: 7.0981
INFO:tensorflow:Assets written to: ./THEMODELassets
Model Created!
The model file created!!!
Please wait! Creating resuşts...
100%|████████████████████████████████████████████████████████████████████| 5160445/5160445 [00:08<00:00, 610910.29it/s]
Process finished. Preparing result file ...
The results are ready.
See MySubmission.csv
Angesichts der Tatsache, dass wir jetzt eine Metrik für die Bewertung der WLAN , aber wir würden stark einen Graph -Clustering -Ansatz vorschlagen.
Betrachten Sie jeden WLAN -Fingerabdruck in den Daten als Knoten in einem Diagramm und können mit anderen Fingerabdrücken im Diagramm eine Kante bilden, indem wir die Ähnlichkeit zweier Fingerabdrücke bewerten. Wir können Kanten ein hohes Gewicht zuweisen, an denen wir eine hohe Ähnlichkeit zwischen Fingerabdrücken und einem niedrigen Gewicht (oder keinem Rand) zwischen denjenigen haben, die nicht ähnlich sind. Theoretisch würde eine perfekt genaue Ähnlichkeitsmetrik trivial trennen, da wir alle Kanten von mehr als 4 Metern ausschließen konnten (ungefähr die Höhe von 1 Stockwerk eines Gebäudes). In Wirklichkeit ist es wahrscheinlich, dass wir falsche Kanten zwischen den Böden machen und diese Kanten irgendwie brechen müssen.
Beginnen wir mit einem einfachen Beispiel. Betrachten Sie das Diagramm unten, in dem die Knotenfarben die wahre Bodenklassifizierung des Fingerabdrucks zeigen und die Kanten widerspiegeln, dass wir glauben, dass diese Knoten auf demselben Boden existieren. Für diese Übung haben wir jede Kante mit seiner "zwischengezogenen Punktzahl" vorbewertet, eine Metrik, die zählt, wie oft diese Kante durch den kürzesten Weg zwischen zwei beliebigen Knoten im Diagramm gegangen ist. In der Regel werden Kanten angezeigt, die auf eine hohe Konnektivität hinweisen und Kandidaten für die Entfernung sein können.
Verwenden Sie in diesem Beispiel den Randwechselness-Score, um die Graph-Kommunen zu erkennen. Geben Sie eine Liste von Listen zurück, in denen jeder Sublist die Knoten -IDs der Gemeinschaften enthält. Beachten Sie, dass dies nur Ihr Verständnis des Problems hilft und nicht für die tatsächliche Lösung zählt.
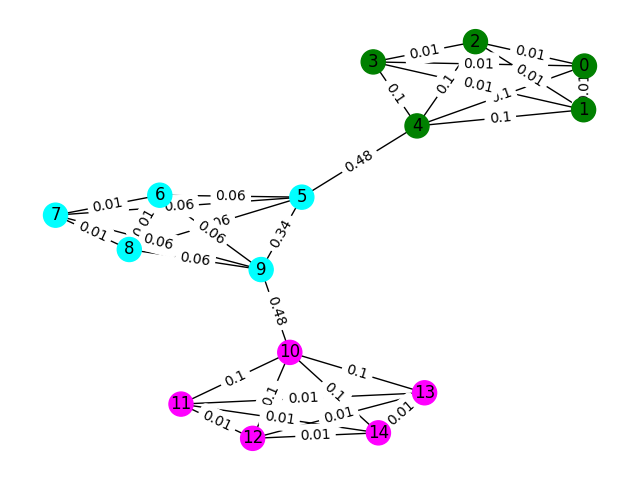
def detect_communities ( Graph ):
## This function should return a list of lists containing
## the node ids of the communities that you have detected.
eb_score = nx . edge_betweenness_centrality ( G )
raise NotImplementedError import networkx as nx
from metrics import check_result
G = nx . read_adjlist ( "graph.adjlist" )
communities = detect_communities ( G )
if check_result ( communities ):
print ( "Correct!" )
else :
print ( "Try again" ) Die Beispieltrainingsdaten für dieses Problem sind ein Satz von 106981 Fingerabdrücken ( task2_train_fingerprints.json ) und einige Kanten zwischen ihnen. Wir haben Dateien bereitgestellt, die drei verschiedene Kantentypen anzeigen, die alle unterschiedlich behandelt werden sollten.
task2_train_steps.csv zeigt Kanten an, die nachfolgende Schritte in einer Flugbahn verbinden. Diese Kanten sollten sehr vertrauenswürdig sein, da sie auf die Gewissheit hinweisen, dass zwei Fingerabdrücke aus demselben Boden aufgezeichnet wurden.
task2_train_elevations.csv geben das Gegenteil der Schritte an. Diese Erhebungen zeigen, dass die Fingerabdrücke fast definitiv aus einem anderen Boden stammen. Sie können das so extrapolieren, wenn Fingerabdruck
task2_train_estimated_wifi_distances.csv sind die vorbereiteten Entfernungen, die wir mit unserer eigenen Distanzmetrik berechnet haben. Diese Metrik ist unvollkommen und als solche wissen wir, dass viele dieser Kanten falsch sein werden (dh sie werden zwei Stockwerke miteinander verbinden). Wir schlagen vor, dass Sie zunächst die Kanten in dieser Datei verwenden, um Ihren Anfangsdiagramm zu konstruieren und eine Lösung zu berechnen. Wenn Sie jedoch eine hohe Punktzahl für Task1 erhalten, können Sie Ihre eigenen WLAN -Entfernungen berechnen, um ein Diagramm zu erstellen.
Ihr Diagramm kann auf einer von zwei Detailebenen liegen, entweder auf der Flugbahnstufe oder auf Fingerabdruckebene. Die Flugbahnstufe hätte jeden Knoten als Flugbahn und Kanten zwischen Knoten würden auftreten, wenn Fingerabdrücke in ihren Flugbahnen eine hohe Ähnlichkeit hätten. Fingerabdruckpegel hätte jeden Fingerabdruck als Knoten. Sie können die Trajektorien -ID des Fingerabdrucks mithilfe der task2_train_lookup.json nach Darstellungen nach Darstellungen suchen.
Um Ihnen zu helfen, Ihre Lösung zu debuggen und zu trainieren, haben wir einige der Trajektorien in task2_train_GT.json eine Grundwahrheit geliefert. In dieser Datei sind die Schlüssel die Trajektorien -IDs (die gleichen wie in task2_train_lookup.json ) und die Werte sind die reale Boden -ID des Gebäudes.
Der Testsatz ist genau das gleiche Format wie das Trainingssatz (für ein separates Gebäude, wir würden es nicht so einfach machen;)), aber wir haben die äquivalente Bodes -Wahrheitsdatei nicht aufgenommen. Dies wird zurückgehalten, damit wir Ihre Lösung bewerten können.
Punkte zu berücksichtigen
In diesem Abschnitt geben wir einen Beispielcode an, um die Dateien zu öffnen und beide Arten von Diagrammen zu konstruieren.
import os
import json
import csv
import networkx as nx
from tqdm import tqdm
path_to_data = "task2_for_participants/train"
with open ( os . path . join ( path_to_data , "task2_train_estimated_wifi_distances.csv" )) as f :
wifi = []
reader = csv . DictReader ( f )
for line in tqdm ( reader ):
wifi . append ([ line [ 'id1' ], line [ 'id2' ], float ( line [ 'estimated_distance' ])])
with open ( os . path . join ( path_to_data , "task2_train_elevations.csv" )) as f :
elevs = []
reader = csv . DictReader ( f )
for line in tqdm ( reader ):
elevs . append ([ line [ 'id1' ], line [ 'id2' ]])
with open ( os . path . join ( path_to_data , "task2_train_steps.csv" )) as f :
steps = []
reader = csv . DictReader ( f )
for line in tqdm ( reader ):
steps . append ([ line [ 'id1' ], line [ 'id2' ], float ( line [ 'displacement' ])])
fp_lookup_path = os . path . join ( path_to_data , "task2_train_lookup.json" )
gt_path = os . path . join ( path_to_data , "task2_train_GT.json" )
with open ( fp_lookup_path ) as f :
fp_lookup = json . load ( f )
with open ( gt_path ) as f :
gt = json . load ( f )
Dies ist eine Möglichkeit, den Diagramm auf Fingerabdruckebene zu konstruieren, wobei jeder Knoten im Diagramm ein Fingerabdruck ist. Wir haben Kantengewichte hinzugefügt, die den geschätzten/echten Entfernungen aus den WLAN- bzw. PDR -Kanten entsprechen. Wir haben auch Höhenkanten hinzugefügt, um diese Beziehung anzuzeigen. Möglicherweise möchten Sie bei der Entwicklung Ihrer Lösung explizit durchsetzen, dass es keine dieser Kanten (oder eine gültige Höhenkante zwischen den Trajektorien) gibt.
G = nx . Graph ()
for id1 , id2 , dist in tqdm ( steps ):
G . add_edge ( id1 , id2 , ty = "s" , weight = dist )
for id1 , id2 , dist in tqdm ( wifi ):
G . add_edge ( id1 , id2 , ty = "w" , weight = dist )
for id1 , id2 in tqdm ( elevs ):
G . add_edge ( id1 , id2 , ty = "e" )Die Flugbahndiagramm ist wohl nicht so einfach, wie Sie sich über eine Möglichkeit nachdenken müssen, um viele WLAN -Verbindungen zwischen Trajektorien darzustellen. In der folgenden Beispielgrafik nehmen wir nur die mittlere Entfernung als Gewicht an, aber ist das wirklich die beste Darstellung?
B = nx . Graph ()
# Get all the trajectory ids from the lookup
valid_nodes = set ( fp_lookup . values ())
for node in valid_nodes :
B . add_node ( node )
# Either add an edge or append the distance to the edge data
for id1 , id2 , dist in tqdm ( wifi ):
if not B . has_edge ( fp_lookup [ str ( id1 )], fp_lookup [ str ( id2 )]):
B . add_edge ( fp_lookup [ str ( id1 )],
fp_lookup [ str ( id2 )],
ty = "w" , weight = [ dist ])
else :
B [ fp_lookup [ str ( id1 )]][ fp_lookup [ str ( id2 )]][ 'weight' ]. append ( dist )
# Compute the mean edge weight
for edge in B . edges ( data = True ):
B [ edge [ 0 ]][ edge [ 1 ]][ 'weight' ] = sum ( B [ edge [ 0 ]][ edge [ 1 ]][ 'weight' ]) / len ( B [ edge [ 0 ]][ edge [ 1 ]][ 'weight' ])
# If you have made a wifi connection between trajectories with an elev, delete the edge
for id1 , id2 in tqdm ( elevs ):
if B . has_edge ( fp_lookup [ str ( id1 )], fp_lookup [ str ( id2 )]):
B . remove_edge ( fp_lookup [ str ( id1 )],
fp_lookup [ str ( id2 )])Ihre Einreichung sollte eine CSV -Datei sein, in der Trajektorien, von denen Sie glauben, dass sie sich auf demselben Boden befinden, ihren Index in derselben Reihe von Kommas getrennt haben. Jeder neue Cluster wird in eine neue Reihe eingegeben.
Siehe zum Beispiel den folgenden zufälligen Eintrag.
import random
random_data = []
n_clusters = random . randint ( 50 , 100 )
for i in range ( 0 , n_clusters ):
random_data . append ([])
for traj in set ( fp_lookup . values ()):
cluster = random . randint ( 0 , n_clusters - 1 )
random_data [ cluster ]. append ( traj )
with open ( "MyRandomSubmission.csv" , "w" , newline = '' ) as f :
csv_writer = csv . writer ( f )
csv_writer . writerows ( random_data )Die Schritte in Aufgabe 2 können wie folgt zusammengefasst werden:
Node2vec vektorisiert.TASK2-Mysubmission.csv ) wird gemäß der Flugbahn von IDs erstellt.Diese Schritte sind im Bild unten dargestellt.

Wir haben Python 3.6.5 verwendet, um die Anwendungsdatei zu erstellen. Wir haben einige zusätzliche Module aufgenommen, die zu Beginn des Wettbewerbs nicht in die Beispieldatei enthalten waren. Diese Module können als:
| Molules | Aufgabe |
|---|---|
| Scikit-Learn | Maschinelles Lernen und Datenvorbereitung |
| node2Vec | Skalierbares Feature -Lernen für Netzwerke |
| Numpy | Mathematische Operationen |
Wir begannen mit der Installation dieser Module als erster Schritt.
## 2.1 Installing modules
!p ip install node2vec
!p ip install scikit - learn
!p ip install numpy In diesem Schritt haben wir den zu verwendeten zufälligen Saatgut festgelegt, um wiederholbare Ergebnisse zu erzielen. Auf diese Weise haben wir einen deterministischen Weg geliefert, auf dem wir in jedem Lauf dasselbe Ergebnis erzielen. Nach unseren Beobachtungen können sich jedoch die Ergebnisse auf verschiedenen Computern leicht unterscheiden (± 1%)
## 2.2 Setting Random Seeds
seed_value = 0
import os
os . environ [ 'PYTHONHASHSEED' ] = str ( seed_value )
import random
random . seed ( seed_value )
import numpy as np
np . random . seed ( seed_value )In diesem Abschnitt werden die für die Testdaten angegebenen Dateien geladen.
wifi -Variable enthält IDs und Gewichte aus der task2_test_estimated_wifi_distances.csv .steps nimmt IDs und Gewichte von Datei task2_test_steps.csv an.elevs Variable entnimmt IDs von Datei auf task2_test_elevations.csv .fp_lookup -Variable erhält IDs und Trajektorien aus der Datei task2_test_lookup.json . Wir haben die Methode zur Neuberechnung der in WLAN angegebenen geschätzten Abstände mit dem in Task1 erhaltenen Modell nicht bevorzugt, da die Ergebnisse, die wir aus diesem Prozess erhalten haben, keinen signifikanten Unterschied machten. Deshalb haben wir die Datei task2_test_fingerprints.json in unserer ultimativen Arbeit nicht verwendet.
## 2.3 Loading the data
import os
import json
import csv
import networkx as nx
from tqdm import tqdm
path_to_data = "task2_for_participants/test"
with open ( os . path . join ( path_to_data , "task2_test_estimated_wifi_distances.csv" )) as f :
wifi = []
reader = csv . DictReader ( f )
for line in tqdm ( reader ):
wifi . append ([ line [ 'id1' ], line [ 'id2' ], float ( line [ 'estimated_distance' ])])
with open ( os . path . join ( path_to_data , "task2_test_elevations.csv" )) as f :
elevs = []
reader = csv . DictReader ( f )
for line in tqdm ( reader ):
elevs . append ([ line [ 'id1' ], line [ 'id2' ]])
with open ( os . path . join ( path_to_data , "task2_test_steps.csv" )) as f :
steps = []
reader = csv . DictReader ( f )
for line in tqdm ( reader ):
steps . append ([ line [ 'id1' ], line [ 'id2' ], float ( line [ 'displacement' ])])
fp_lookup_path = os . path . join ( path_to_data , "task2_test_lookup.json" )
with open ( fp_lookup_path ) as f :
fp_lookup = json . load ( f ) 3773297it [00:19, 191689.25it/s]
2767it [00:00, 52461.27it/s]
139537it [00:00, 180082.01it/s]
Wir nehmen die durchschnittliche Entfernung als Gewicht bei, wenn wir das Flugbahndiagramm erstellen. Wir haben das Beispiel für Aufgabe 2 ( Task2-IPS-Challenge-2021.ipynb ) für diesen Prozess verwendet. Wir haben das resultierende Diagramm ( B ) als Adjazenzliste im Verzeichnis (als my.adjlist ) gespeichert.
## 2.3 Generating the Trajectory graph.
B = nx . Graph ()
# Get all the trajectory ids from the lookup
valid_nodes = set ( fp_lookup . values ())
for node in valid_nodes :
B . add_node ( node )
# Either add an edge or append the distance to the edge data
for id1 , id2 , dist in tqdm ( wifi ):
if not B . has_edge ( fp_lookup [ str ( id1 )], fp_lookup [ str ( id2 )]):
B . add_edge ( fp_lookup [ str ( id1 )],
fp_lookup [ str ( id2 )],
ty = "w" , weight = [ dist ])
else :
B [ fp_lookup [ str ( id1 )]][ fp_lookup [ str ( id2 )]][ 'weight' ]. append ( dist )
# Compute the mean edge weight
for edge in B . edges ( data = True ):
B [ edge [ 0 ]][ edge [ 1 ]][ 'weight' ] = sum ( B [ edge [ 0 ]][ edge [ 1 ]][ 'weight' ]) / len ( B [ edge [ 0 ]][ edge [ 1 ]][ 'weight' ])
# If you have made a wifi connection between trajectories with an elev, delete the edge
for id1 , id2 in tqdm ( elevs ):
if B . has_edge ( fp_lookup [ str ( id1 )], fp_lookup [ str ( id2 )]):
B . remove_edge ( fp_lookup [ str ( id1 )],
fp_lookup [ str ( id2 )])
nx . write_adjlist ( B , "my.adjlist" ) 100%|████████████████████████████████████████████████████████████████████| 3773297/3773297 [00:27<00:00, 135453.95it/s]
100%|██████████████████████████████████████████████████████████████████████████████████████| 2767/2767 [00:00<?, ?it/s]
Bevor wir die Adjazenzliste als Eingabe für die Algorithmen für maschinelles Lernen geben, wandeln wir die Knoten in Vektor um. In unserer Arbeit verwendeten wir Node2VEC als Graph -Einbettungsalgorithmus -Methodik, die 2016 von Grover & Leskovec vorgeschlagen wurde [3]. NODE2VEC ist ein halbüberwachender Algorithmus zum Lernen der Knoten im Netzwerk. NODE2VEC wird basierend auf der Skip-Gram-Technik erstellt, bei der es sich um einen NLP-Ansatz handelt, der auf der Verteilungsstrukturkonzept motiviert ist. Wenn Sie sich in ähnlichen Kontexten in ähnlichen Kontexten befinden, haben sie wahrscheinlich eine ähnliche Bedeutung und es gibt eine offensichtliche Beziehung zwischen ihnen. Skip-Gram-Technik verwendet das Mittelwort (Eingabe), um Nachbarn (Ausgabe) vorherzusagen, während die Wahrscheinlichkeiten der Umgebung basierend auf einer bestimmten Fenstergröße (zusammenhängende Abfolge von Elementen zuvor nach der Mitte) berechnet werden, mit anderen Worten n-Gramm. Im Gegensatz zum NLP -Ansatz wird das NODE2VEC -System nicht mit Wörtern gefüttert, die eine lineare Struktur haben, sondern Knoten und Kanten, die eine verteilte grafische Struktur haben. Diese mehrdimensionale Struktur macht Einbettdings komplex und rechnerisch teuer, aber NODE2VEC verwendet negative Abtastungen mit optimierender stochastischer Gradientenabstieg (SGD), um damit umzugehen. Darüber hinaus wird der zufällige Walk -Ansatz verwendet, um die benachbarten Probeknoten des Quellknotens in einer nichtlinearen Struktur zu erkennen.
In unserer Studie führten wir zunächst die Vektorrepräsentation von Knotenbeziehungen im niedrigdimensionalen Raum durch, indem wir mit NODE2VEC aus dem gegebenen Abstand von zwei Knoten (Gewichten) modellieren. Anschließend verwendeten wir den Ausgang von NODE2VEC (Graph-Einbettungen), das Vektoren von Knoten enthält, um den traditionellen K-Mittel-Clustering-Algorithmus zu füttern.
Die Parameter, die wir in NOD2VEC verwenden, können wie folgt aufgeführt werden:
| Hyperparameter | Wert |
|---|---|
| Abmessungen | 32 |
| Walk_length | 15 |
| num_walks | 100 |
| Arbeiter | 1 |
| Samen | 0 |
| Fenster | 10 |
| min_count | 1 |
| batch_words | 4 |
Das Node2VEC-Modell nimmt die Adjazenzliste als Eingabe an und gibt einen Vektor mit 32 Größe aus. In diesem Teil wird die Datei node.py erstellt und im Jupyter Notebook ausgeführt. Es gibt zwei Gründe, warum es vorzuziehen ist, extern und in einer Jupyter -Notebook -Zelle extern zu laufen.
Node2vec ist eine sehr rechnerisch teure Methode. Der RAM -Überlauffehler ist durchaus möglich, wenn Sie in Jupyter Notebook ausgeführt werden. Das Erstellen und Ausführen Node2vec -Modell im Freien vermeidet diesen Fehler. Die folgende Zelle erstellt die Datei mit dem Namen node.py. Diese Datei erstellt das node2VEC -Modell. Dieses Modell nimmt die Adjazenzliste ( my.adjlist ) als Eingabe an und erstellt eine 32-dimensionale Vektordatei als Ausgabe ( vectors.emb ).
Wichtig! Der folgende Code sollte in Linux -Verteilungen ausgeführt werden (getestet in Google Colab und Ubuntu).
# 2.4 Converting nodes to vectors
# A folder named tmp is created. This folder is essential for the node2vec model to use less RAM.
try :
if not os . path . exists ( "tmp" ):
os . makedirs ( "tmp" )
except OSError :
print ( "The folder could not be created! n Please manually create the " tmp " folder in the directory" )
node = """
# importing related modules
from node2vec import Node2Vec
import networkx as nx
#importing adjacency list file as B
B = nx.read_adjlist("my.adjlist")
seed_value=0
# Specifying the input and hyperparameters of the node2vec model
node2vec = Node2Vec(B, dimensions=32, walk_length=15, num_walks=100, workers=1,seed=seed_value,temp_folder = './tmp')
#Assigning/specifying random seeds
import os
os.environ['PYTHONHASHSEED']=str(seed_value)
import random
random.seed(seed_value)
import numpy as np
np.random.seed(seed_value)
# creation of the model
model = node2vec.fit(window=10, min_count=1, batch_words=4,seed=seed_value)
# saving the output vector
model.wv.save_word2vec_format("vectors.emb")
# save the model
model.save("vectorMODEL")
"""
f = open ( "node.py" , "w" )
f . write ( node )
f . close ()
! PYTHONHASHSEED = 0 python3 node . py Nachdem unsere Vektordatei erstellt wurde, lesen wir diese Datei ( vectors.emb ). Diese Datei besteht aus 33 Spalten. Die erste Spalte ist die Knotennummer (IDS) und die Reste sind Vektorwerte. Durch Sortieren der gesamten Datei nach der ersten Spalte geben wir die Knoten in ihre ursprüngliche Bestellung zurück. Dann löschen wir diese ID -Spalte, die wir nicht mehr verwenden werden. Wir geben also die endgültige Form unserer Daten an. Unsere Daten können in Anwendungen für maschinelles Lernen verwendet werden.
# 2.4 Reshaping data
vec = np . loadtxt ( "vectors.emb" , skiprows = 1 )
print ( "shape of vector file: " , vec . shape )
print ( vec )
vec = vec [ vec [:, 0 ]. argsort ()];
vec = vec [ 0 : vec . shape [ 0 ], 1 : vec . shape [ 1 ]] shape of vector file: (11162, 33)
[[ 9.1200000e+03 3.9031842e-01 -4.7147268e-01 ... -5.7490986e-02
1.3059708e-01 -5.4280665e-02]
[ 6.5320000e+03 -3.5591956e-02 -9.8558587e-01 ... -2.7217887e-02
5.6435770e-01 -5.7787680e-01]
[ 5.6580000e+03 3.5879680e-01 -4.7564098e-01 ... -9.7607370e-02
1.5506668e-01 1.1333219e-01]
...
[ 2.7950000e+03 1.1724627e-02 1.0272172e-02 ... -4.5596390e-04
-1.1507459e-02 -7.6738600e-04]
[ 4.3380000e+03 1.2865483e-02 1.2103912e-02 ... 1.6619096e-03
1.3672550e-02 1.4605848e-02]
[ 1.1770000e+03 -1.3707868e-03 1.5238028e-02 ... -5.9994194e-04
-1.2986251e-02 1.3706315e-03]]
Task-2 ist ein Clustering-Problem. Die Prämisse, die wir bei der Lösung dieses Problems entscheiden müssen, ist, wie viele Cluster wir teilen sollten. Dafür haben wir verschiedene Cluster -Zahlen ausprobiert und die Punkte verglichen, die wir erhielten. Die folgende Grafik zeigt den Vergleich der Anzahl der Cluster und der erhaltenen Punktzahl. Wie aus dieser Grafik hervorgeht, stieg die Anzahl der Cluster mit einigen Ausnahmeschwankungen kontinuierlich zwischen 5 und 21 und stabilisierte sich nach 21 Jahren. Aus diesem Grund haben wir uns auf die Anzahl der Cluster zwischen 21 und 23 in unserer Studie konzentriert.
# 2.5 Determine the number of clusters
import numpy as np
import matplotlib . pyplot as plt
import seaborn as sns
import matplotlib
% matplotlib inline
sns . set_style ( "whitegrid" )
agglom = [ 24.69 , 28.14 , 28.14 , 28.14 , 30 , 33.33 , 40.88 , 38.70 , 40 , 40 , 40 , 29.12 , 45.85 , 45.85 , 48.00 , 50.17 , 57.83 , 57.83 , 57.83 ]
plt . figure ( figsize = ( 10 , 5 ))
plt . plot ( range ( 5 , 24 ), agglom )
matplotlib . pyplot . xticks ( range ( 5 , 24 ))
plt . title ( 'Number of clusters and performance relationship' )
plt . xlabel ( 'Number of clusters' )
plt . ylabel ( 'Score' )
plt . show ()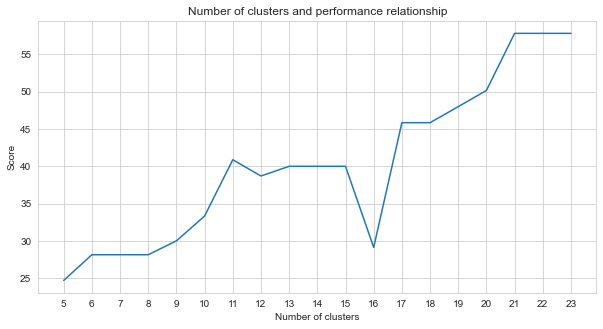
Unter den unbeaufsichtigten Methoden des maschinellen Lernens, die wir ausprobiert haben (z. mit 23 Clustern.
K-Means ist ein Clustering-Algorithmus. Cluster sollen Punkte (Knoten in unseren Daten) gruppieren, die bestimmte Ähnlichkeiten aufweisen. K-Means benötigt die Zielzahl von Schwerpunkten, was sich darauf bezieht, wie viele Gruppen die Daten unterteilt werden sollten. Der Algorithmus beginnt mit der Gruppe zufällig zugewiesener Zentroide und setzt dann die Iterationen fort, um die besten Positionen davon zu finden. Der Algorithmus weist den festgelegten Zentroiden die Punkte/Knoten mit der Summe der Quadrate des Mitglieds von Punkten zu. Dies wird weiterhin aktualisiert und verschoben [4]. In unserem Beispiel spiegelt die Anzahl der Schwerpunkte die Anzahl der Böden wider. Es ist zu beachten, dass dies keine Informationen über die Reihenfolge der Böden liefert.
Im Folgenden wurde die K-Means-Anwendung für 23 Cluster gestellt.
# 2.5 Best result
from sklearn import cluster
import time
ML_results = []
k_clusters = 23
algorithms = {}
algorithms [ 'KMeans' ] = cluster . KMeans ( n_clusters = k_clusters , random_state = 10 )
second = time . time ()
for model in algorithms . values ():
model . fit ( vec )
ML_results = list ( model . labels_ )
print ( model , time . time () - second ) KMeans(n_clusters=23, random_state=10) 1.082334280014038
Die Ausgabe des Algorithmus für maschinelles Lernen bestimmt, zu welchem Cluster die Fingerabdrücke gehören. Aber was von uns verlangt wird, ist, die Flugbahnen zu gruppieren. Daher werden diese Fingerabdrücke unter Verwendung der Variablen fp_lookup in ihre Trajektorien -Gegenstücke konvertiert. Diese Ausgabe wird in die Datei TASK2-Mysubmission.csv verarbeitet.
## 2.6 Submission
result = {}
for ii , i in enumerate ( set ( fp_lookup . values ())):
result [ i ] = ML_results [ ii ]
ters = {}
for i in result :
if result [ i ] not in ters :
ters [ result [ i ]] = []
ters [ result [ i ]]. append ( i )
else :
ters [ result [ i ]]. append ( i )
final_results = []
for i in ters :
final_results . append ( ters [ i ])
name = "TASK2-Mysubmission.csv"
with open ( name , "w" , newline = '' ) as f :
csv_writer = csv . writer ( f )
csv_writer . writerows ( final_results )
print ( name , "file is ready!" ) TASK2-Mysubmission.csv file is ready!
[1] P. Virtanen und Scipy 1.0 -Mitwirkende. Scipy 1.0: Grundlegende Algorithmen für wissenschaftliches Computer in Python. Naturmethoden, 17: 261--272, 2020.
[2] A. Geron, praktisches maschinelles Lernen mit Scikit-Learn, Keras und Tensorflow: Konzepte, Werkzeuge und Techniken zum Aufbau intelligenter Systeme. O'Reilly Media, 2019
[3] A. Grover, J. Leskovec. ACM SIGKDD Internationaler Konferenz über Wissensentdeckung und Data Mining (KDD), 2016.
[4] Jin X., Han J. (2011) K-Means-Clustering. In: Sammut C., Webb GI (Hrsg.) Encyclopedia des maschinellen Lernens. Springer, Boston, MA. https://doi.org/10.1007/978-0-387-30164-8_425