
Über das Projekt
Tech Stack
Dateistruktur
Erste Schritte
Ergebnisse und Demo
Zukünftige Arbeit
Mitwirkende
Anerkennung und Ressourcen
Lizenz
Das Geräusch musste entfernt werden, das natürlich induziert ist wie das nicht umweltbezogene Rauschen, das mit dem Denoing des Signals entfernt wird. Siehe diese Dokumentation auch diesen Blog zur Reduzierung von AI -Rauschen
Die Librosa -Bibliothek für Audio -Manupulation wird verwendet.
Für die Audiosignale haben wir Scipy verwendet
Matplotlib verwendet, um die Daten zu manipulieren und das Signal zu visualisieren.
Der Rest ist numpy für mathematische Operationen, Welle für das Betrieb in der Wellendatei.
Noise Reduction ├───docs ## Documents and Images │ └───Input Audio file ├─── Project Details │ | │ ├─── │ │ ├───Research papers │ │ ├───Linear Algebra │ │ ├───Neural networks & Deep Learning │ │ ├───Project Documentation │ │ ├───AI Noise Reduction Blog │ │ ├───AI Noise Reduction Report │ │ └───Code Implementation │ │ ├───AI Noise Reduction.py │ │ ├───audio.wav │ │ ├───Resources
Unter Windows getestet
Git Clone https://github.com/dhriti03/noise-rection.gitcd Rauschen-rektion
Installieren Sie in Ihrem Notebook bestimmte Bibliotheken
PIP -Welle installieren PIP Installieren Sie Librosa pip install install scipy.io PIP Installieren Sie Matplotlib.PyPlot
*Dies ist die ursprüngliche Audiodatei * *  *Nach Zugabe des Rauschens * *
*Nach Zugabe des Rauschens * *  *Das endgültige Audiosignal nach dem Entfernen von Rauschen * *
*Das endgültige Audiosignal nach dem Entfernen von Rauschen * *  *Flowdiagramm für das Projekt *
*Flowdiagramm für das Projekt * 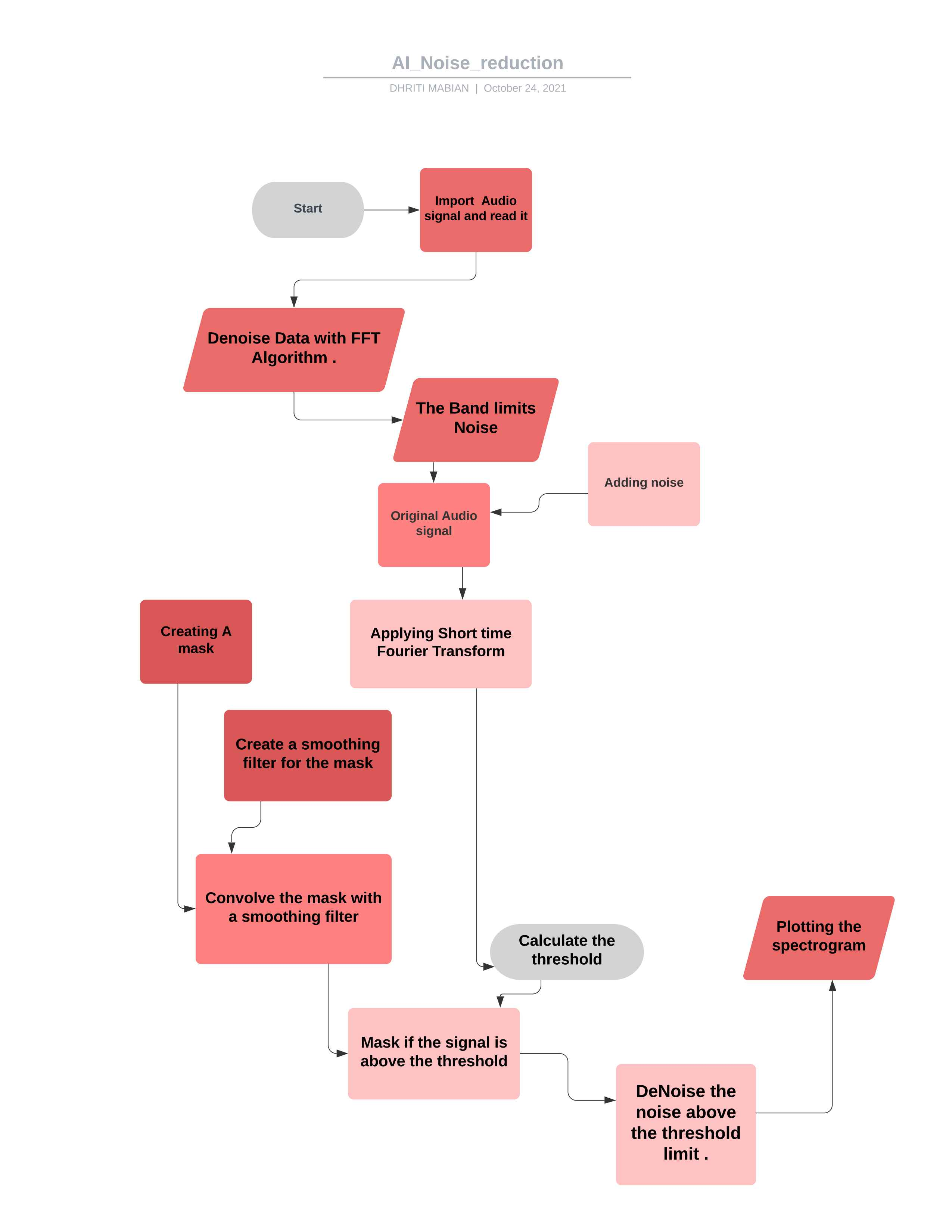
Wenn Sie den Code entsprechend Ihren Anforderungen manipulieren, können Sie ihn verwenden, um die meisten Audio -Signlas zu steuern. ##Theorie
Ein FFT wird über den Rausch -Audioclip berechnet
Statistiken werden über FFT des Rauschens berechnet (in Frequenz)
Ein Schwellenwert wird basierend auf den Statistiken des Rauschens (und der gewünschten Empfindlichkeit des Algorithmus) berechnet.
Eine Maske wird durch Vergleich des Signal -FFT mit der Schwelle bestimmt
Die Maske wird über Frequenz und Zeit mit einem Filter geglättet
Die Maske wird auf die FFT des Signals angereichert und invertiert
Import Ipython von scipy.io import WavFileMport scipy.Signalimport
Hier importieren wir die Bibliotheken wie die ipython lib, die verwendet wird, um eine umfassende Umgebung für interaktives und exploratives Computing zu schaffen.
Aus der scipy.IO -Bibliothek wird zur Manipulation der Daten und zur Visualisierung der Daten mithilfe einer Vielzahl von Python -Befehlen verwendet.
Numpy enthält ein mehrdimensionales Array- und Matrixdatenstrukturen. Es kann verwendet werden, um eine Reihe von mathematischen Operationen in Arrays wie trigonometrischen, statistischen und algebraischen Routinen auszuführen. Daher ist eine sehr nützliche Bibliothek.
Matplotlib.PyPlot -Bibliothek hilft, die große Menge an Daten durch unterschiedliche Visualisierungen zu verstehen.
Librosa verwendet, wenn wir mit Audiodaten wie in der Musikgenerierung (mit LSTMs) arbeiten, automatische Spracherkennung. Es bietet die Bausteine, die zur Erstellung der Abrufsysteme für Musikinformationen erforderlich sind.
%Matplotlib -Inline, um das Inline -Ploting zu aktivieren, wobei die Diagramme/Diagramme direkt unter der Zelle angezeigt werden, in der Ihre Handlungsbefehle geschrieben werden. Es bietet Interaktivität mit dem Backend in den Frontenden wie dem Jupyter -Notizbuch.
WAV_LOC = R '/HOME/ROICE_REDUKTION/DOWNLOWS/WAVE/DATEI.WAV'RATE, DATA = WAVFILE.READ (WAV_LOC, MMAP = FALSCH)
Hier nehmen wir den WAW -Dateipfadspeicherort an und lesen dann diese WAW -Datei mit dem Wavefile -Modul, das aus der Scipy.io -Bibliothek stammt. Mit Parametern (Dateiname - String oder Öffnen von Dateihandle, die eine Eingabered -WAV -Datei ist). Dann (MMAP: bool, optional, ob Daten als Speicher -Made (Standard: Falsch) gelesen werden sollen.
Def fftnoise (f): f = np.Array (f, dtype = "komplex") np = (len (f) - 1) // 2phasen = np.random.rand (np) * 2 * np.piphasen = np .Cos (Phasen) + 1J * np.sin (Phasen) f [1: np + 1] * = PhaseSF [-1: -1 -np: -1] = np.conj (f [1: np + 1] ) return np.fft.ifft (f) .real
Hier definieren wir zunächst die FFT -Rauschfunktion kurz, eine schnelle Fourier -Transformation (FFT) ist ein Algorithmus, der die diskrete Fourier -Transformation (DFT) einer Sequenz oder ihre Inverse (IDFT) berechnet. Die Fourier -Analyse wandelt ein Signal aus seiner ursprünglichen Domäne (oft Zeit oder Raum) in eine Darstellung in der Frequenzdomäne um und umgekehrt. Das DFT wird erhalten, indem eine Sequenz von Werten in Komponenten unterschiedlicher Frequenzen zerlegt wird.
Verwenden von Fast Fourier -Transformation und Definieren einer Funktion des Datentypkomplexes und schließlich Berechnung des tatsächlichen Teils der Funktion. Darin werden die Frequenzen zwischen der Mindestfrequenz und der maximalen Frequenz auf 1 eingestellt und ruhen unerwünscht.
Angeben des Dateispeichers
Lesen der WAV -Datei
-32767 bis +32767 ist ordnungsgemäßes Audio (symmetrisch) und 32768 bedeutet, dass der Audio an diesem Punkt abgeschnitten wurde
WAV-File ist 16-Bit-Ganzzahl, der Bereich beträgt [-32768, 32767], wodurch durch 32768 (2^15) den ordnungsgemäßen Bereich von [-1, 1] geteilt wird.
DEF band_limited_noise (min_freq, max_freq, sample = 1024, sampled = 1): freqs = np.abs (np.fft.fftfreq (proben, 1 / sample) f = np.zeros (Samples) f [np.logical_and (freeqs (freeqs > = min_freq, freqs <= max_freq)] = 1return fftnoise (f)
Eine Funktions- oder Zeitreihe, deren Fourier -Transformation auf einen endlichen Bereich von Frequenzen oder Wellenlängen beschränkt ist.
Definieren des FREQ mit dem Standard -Freq mit der min- und maximalen Grenze.
Rauschen_len = 2 # SecondsNoise = band_limited_noise (min_freq = 4000, max_freq = 12000, sample = len (data), sampled = rate)*10noise_clip = rauschen [: rate*rauschen] audio_clip_limited = data+rauschen
Der bandbegrenzte weiße Rauschblock gibt ein zweiseitiges Spektrum an, bei dem die Einheiten Hz sind.
wobei der maximale von 12000 und min Freq von 4000 mit dem Rauschen und den bereitgestellten Daten verglichen wird.
Hier schneiden wir das Rauschsignal aus, indem wir ein Produkt der Geschwindigkeit und des Len -Rauschsignals haben.
So addieren Sie das Rauschen und die angegebenen Daten
Das Hinzufügen von Rauschen erweitert die Größe des Trainingsdatensatzes.
Zu den Eingangsvariablen wird zufälliges Rauschen hinzugefügt, wodurch sie jedes Mal unterschiedlich sind, wenn es dem Modell ausgesetzt ist.
Das Hinzufügen von Rauschen zu Eingangsproben ist eine einfache Form der Datenerweiterung.
Hinzufügen von Rauschen bedeutet, dass das Netzwerk weniger in der Lage ist, sich Trainingsproben auswendig zu merken, da es die ganze Zeit verändert.
Dies führt zu kleineren Netzwerkgewichten und einem robusteren Netzwerk mit geringeren Verallgemeinerungsfehlern.
Zeit von DateTime importieren timedelta als td importieren
Importzeit Dieses Modul bietet verschiedene zeitbezogene Funktionen. Für die verwandte Funktionalität siehe auch die Module DateTime und Kalender. Klasse DateTime.Timedelta
Eine Dauer, die den Unterschied zwischen zwei Datums-, Uhrzeit- oder DateTime -Instanzen zur Auflösung von Mikrosekunden ausdrückt.
def _stft (y, n_fft, hop_length, win_length): return librosa.stft (y = y, n_fft = n_fft, hop_length = hop_length, Win_Length = Win_Length)
Kurzzeit -Fourier -Transformation kann verwendet werden, um die Änderung der Frequenz und des Phasengehalts eines nichtstationären Signals im Laufe der Zeit zu quantifizieren.
Die Hopfenlänge sollte sich auf die Anzahl der Proben zwischen aufeinanderfolgenden Rahmen beziehen. Für die Signalanalyse sollte die Hopfenlänge geringer sein als die Rahmengröße, so dass sich die Rahmen überlappen.
Parameter ynp.ndarray [Shape = (n,)], reales Eingangssignal
n_fftint> 0 [Scalar]
Länge des Fenstersignals nach dem Polsterung mit Nullen. Die Anzahl der Zeilen in der STFT -Matrix d ist (1 + n_fft/2) . Der Standardwert n_fft = 2048 Proben entspricht einer physischen Dauer von 93 Millisekunden mit einer Stichprobenrate von 22050 Hz, dh der Standardabstichrate in Librosa. Dieser Wert ist gut für Musiksignale angepasst. In der Sprachverarbeitung beträgt der empfohlene Wert jedoch 512, was 23 Millisekunden mit einer Stichprobenrate von 22050 Hz entspricht. In jedem Fall empfehlen wir, N_FFT auf eine Leistung von zwei zu setzen, um die Geschwindigkeit des FAST Fourier -Transformationsalgorithmus (FFT) zu optimieren.
hop_lengthint> 0 [scalar]
Anzahl der Audioproben zwischen benachbarten STFT -Spalten.
Kleinere Werte erhöhen die Anzahl der Spalten in D, ohne die Frequenzauflösung des STFT zu beeinflussen.
Bei nicht spezifiziertem Standardwert zu Win_Length // 4 (siehe unten).
win_lengthint <= n_fft [scalar]
Jeder Audio -Frame wird mit einem Fenster der Länge win_length fenstert und dann mit Nullen gepolstert, um mit N_FFT übereinzustimmen.
Kleinere Werte verbessern die zeitliche Auflösung des STFT (dh die Fähigkeit, Impulse zu unterscheiden, die zeitlich eng verteilt sind) auf Kosten der Frequenzauflösung (dh die Fähigkeit, reine Töne zu unterscheiden, die in der Frequenz eng verteilt sind). Dieser Effekt wird als Kompromiss für die Zeitfrequenzlokalisierung bezeichnet und muss entsprechend den Eigenschaften des Eingangssignals y angepasst werden.
Bei nicht spezifiziertem Standardwert zu Win_Length = n_fft .
return librosa.istft (y, hop_length, win_length)
Inverse Kurzzeit-Fourier-Transformation (ISTFT). Konvertiert komplexe Wertschöpfungsspektrogramm STFT_MATRIX in die Zeitreihe Y, indem der mittlere quadratische Fehler zwischen STFT_MATRIX und STFT von Y minimiert wird, wie in beschrieben in beschrieben
Im Allgemeinen sollten die Fensterfunktion, die Hopfenlänge und andere Parameter wie in STFT sein, was hauptsächlich zu einer perfekten Rekonstruktion eines Signals von unmodifiziertem STFT_Matrix führt.
Def _amp_to_db (x): return librosa.core.amplitude_to_db (x, ref = 1.0, amin = 1e-20, top_db = 80.0)
1. Verbinden Sie ein Amplitudenspektrogramm in das DB-skalierte Spektrogramm. Dies entspricht Power_to_db (S ** 2), wird jedoch für die Bequemlichkeit bereitgestellt.
return librosa.core.db_to_amplitude (x, ref = 1.0)
Konvertieren Sie ein DB-skaliertes Spektrogramm in ein Amplitudenspektrogramm.
Dies kehrt effektiv amplitude_to_db um:
db_to_amplitude (s_db) ~ = 10.0 (0,5* (s_db + log10 (ref)/10)) **
DEF -Plot_Spectrogramm (Signal, Titel): Abb, ax = plt.subPlots (AbbSize = (20, 4)) Cax = Ax.Matshow (Signal, Origin = "Lower", Aspekt = "Auto", CMAP = PLT.CM. seismisch, vmin = -1 * np.max (np.abs (Signal)), vmax = np.max (np.abs (Signal)),,
)Das Spektogramm mit Signal als Eingang darstellen.
Die Achsenklasse enthält die meisten Figurenelemente: Achse, Tick, Zeile2d, Text, Polygon usw. und legt das Koordinatensystem fest.
Es bietet mehrere Farbkarten in Matplotlib, die über diese Funktion zugänglich sind.
Abb.Colorbar (CAX) AX.SET_TITLE (Titel)
Der beste Weg, um zu sehen, was passiert, besteht darin, eine Farbleiste hinzuzufügen (PLT.Colorbar (), nachdem er das Streudiagramm erstellt hat). Sie werden feststellen, dass Ihre Out -Werte zwischen 0 und 10000 unter dem niedrigsten Teil der Stange liegen, wo die Dinge sehr hellgrün sind.
Im Allgemeinen werden die Werte unter VMIN mit der niedrigsten Farbe gefärbt, und die Werte über VMAX erhalten die höchste Farbe.
Wenn Sie VMAX kleiner als Vmin einstellen, werden sie intern ausgetauscht. Abhängig von der genauen Version von Matplotlib und den genannten genauen Funktionen kann Matplotlib eine Fehlerwarnung geben. Also am besten, um Vmin immer niedriger zu machen als Vmax.
Def Plot_Statistics_and_filter (Mean_Freq_noise, STD_FREQ_NOISE, Rauschen_Thresh, Smoothing_filter): Abb, ax = plt.subplots (ncols = 2, figsize = (20, 4) PLT_STD, = AX [0]. von Rauschen ")
PLT_STD, = AX [0] .PLOT (Rauschen_Thresh, Label = "Rauschschwelle (nach Frequenz)") AX [0] .set_title ("Schwelle für Maske")
ax [0] .Legend () CAX = AX [1] .MATSHOW (glättlich_filter, Origin = "Lower") Abb.Colorbar (CAX) AX [1] .set_title ("Filter für die Glättungsmaske"))Grundstücke grundlegende Statistiken zur Rauschreduzierung.
Das Signal-Rausch-Verhältnis (SNR oder S/N) ist ein Maß in Wissenschaft und Ingenieurwesen, das den Niveau eines gewünschten Signals mit dem Niveau des Hintergrundrauschens vergleicht.
SNR ist definiert als das Verhältnis der Signalleistung zur Rauschleistung, die häufig in Dezibel exprimiert wird.
Ein Verhältnis von mehr als 1: 1 (größer als 0 dB) zeigt mehr Signal als Rauschen an.
Einrichten der Häufigkeit von Schwächen für die Lärmmaskierung.
Die Maskierungsschwelle bezieht sich auf einen Prozess, bei dem ein Klang aufgrund der Anwesenheit eines anderen Klangs unhörbar gemacht wird.
Die Maskierungsschwelle ist also der Schalldruckpegel eines Geräusches, das benötigt wird, um das Sound in Gegenwart eines anderen Rauschens, der als "Masker" bezeichnet wird, hörbar zu machen.
So fügte die Schwelle hinzu.
Unschärfe -Geräuschsignale mit verschiedenen Passfiltern
Wenden Sie kundenspezifische Filter auf Bilder an (2D-Faltung)
Def removenoise ( # zum Durchschnitt des Signals (Spannung) des positiven Slope-Teils (Anstieg) einer Dreieckswelle, um zu versuchen, so viel Rauschen wie möglich zu entfernen. Audio_Clip, # Diese Clips sind die verwendet Operations Rauschen_Clip, n_grad_freq = 2, # Wie viele Frequenzkanäle, die mit der Maske glätten sollen. N_grad_time = 4, # Wie viele Zeitkanäle, die mit der Maske glätten können. 2048, # Jeder Audio -Rahmen wird von `window ()` besiedelt. n_std_thresh = 1.5, # Wie viele Standardabweichungen lauter als der mittlere dB des Rauschens (bei jedem Frequenzstufe) als SignalProp_decrease = 1.0, #to, in welchem Ausmaß, in welchem Ausmaß Sie das Rauschen verringern sollten (1 = alle, 0 = keine) Verbose = false Mit # Flag können Sie regelmäßige Ausdrücke schreiben, die präsablevisual = false aussehen, #fall, um die Schritte des Algorithmus zu zeichnen):
Def removenoise ( zum Durchschnitt des Signals (Spannung) des positiven Slope-Teils (Anstieg) einer Dreieckswelle, um zu versuchen, so viel Rauschen wie möglich zu entfernen.
audio_clip,
Diese Clips sind die verwendeten Parameter, für die wir die jeweiligen Operationen ausführen würden
Noise_clip, n_grad_freq = 2 Wie viele Frequenzkanäle, die mit der Maske geglättet sind.
n_grad_time = 4, wie viele Zeitkanäle, die mit der Maske geglättet sind.
n_fft = 2048
Nummer Audio von Frames zwischen STFT -Spalten.
win_length = 2048, jeder Audio -Frame wird von window() fensteriert. Das Fenster wird von Länge win_length und dann mit Nullen gepolstert, um n_fft zu entsprechen.
Hop_length = 512, Zahl Audio von Frames zwischen STFT -Spalten.
n_std_thresh = 1.5 Wie viele Standardabweichungen lauter als der mittlere dB des Rauschens (zu jedem Frequenzpegel) als Signal betrachtet werden
prop_decrease = 1.0, in welchem Umfang sollte Sie das Rauschen verringern (1 = alle, 0 = keine)
wörtlich = falsch,
Mit Flag können Sie regelmäßige Ausdrücke schreiben, die präsentierbar aussehen, visual = false, ob die Schritte des Algorithmus geplant werden können):
Noise_Stft = _stft (Rauschen_Clip, N_fft, Hop_Length, Win_Length) Rauschen_stft_db = _amp_to_db (np.abs (Rauschen_Stft))
Stft über Lärm
in DB konvertieren
Mean_freq_noise = np.mean (rauschen_stft_db, axis = 1) std_freq_noise = np.std (rauschen_stft_db, axis = 1) rauschen_thresh = mean_freq_noise + std_freq_noise * n_std_thresh_thresh_thresh_thresh_thresh
Berechnen Sie die Statistiken über Rauschen
Hier fügen wir für das Thresh -Rauschen den Mittelwert und das Standardrauschen und das N_STD -Rauschen hinzu.
sig_stft = _stft (audio_clip, n_fft, hop_length, win_length) sig_stft_db = _amp_to_db (np.abs (sig_stft))
STFT über Signal
mask_gain_db = np.min (_amp_to_db (np.abs (sig_stft)))
Berechnen Sie den Wert, um DB auf zu maskieren
Smoothing_Filter = NP.OUTER (NP.Concatenate (
[np.linspace (0, 1, n_grad_freq + 1, endpoint = false), np.linspace (1, 0, n_grad_freq + 2),
]
) [1: -1], np.concatenate (
[np.linspace (0, 1, n_grad_time + 1, endpoint = false), np.linspace (1, 0, n_grad_time + 2),
]
) [1: -1],
) Smoothing_Filter = Smoothing_filter / np.sum (Smoothing_Filter)Erstellen Sie einen Glättungsfilter für die Maske in Zeit und Frequenz
db_thresh = np.repeat (np.reshape (rauschen_thresh, [1, len (mean_freq_noise)]), np.shape (sig_stft_db) [1], axis = 0,
).TBerechnen Sie den Schwellenwert für jeden Frequenz-/Zeitbehälter
sig_mask = sig_stft_db <db_thresh
Maske für das Signal
SIG_Mask = scipy.Signal.fftconvolve (Sig_mask, Smoothing_filter, modus = "gleich") sig_mask = sig_mask * prop_decrease
Maske Faltung mit Glättungsfilter
# Mask the SignalSIG_STFT_DB_Masked = (sig_stft_db _to_amp (sig_stft_db_masked) * np.sign (sig_stft)) + (1j * sig_imag_masked)
Maskieren Sie das Signal
# Wiederherstellen Sie die SignalRecovered_signal = _istft (sig_stft_amp, hop_length, Win_Length) Recoteed_spec = _amp_to_db (np.abs (_stft (recoteed_signal, n_fft, hop_length, win_length))
)das Signal wiederherstellen
Wenden Sie also die Maske an, wenn das Signal über der Schwelle liegt
Verpacken Sie die Maske mit einem Glättungsfilter
Anwenden des Rauschreduzierungsalgorithums für die bereits heruntergeladene WAV -Datei.
Anwenden der FFT über die Live -Aufzeichnung des Audiosignals.
Weitere tiefe Umsetzung der KI für die Rauschunterdrückung.
Anwenden des Rauschreduzierungsalgorithums für verschiedene Formate von Audiodateien.
Das Live -Audiosignal mit dem Mikrofon und der ESP32 und somit wird die WAV -Datei für die weitere Berechnung und Signalverarbeitung erhalten.
Dhriti Mabian
Priyal Awankar
*Sra vjti_eklavya 2021
Shreyas atre
Hart Shah
Kühnheit
Rauschunterdrückungsmethode
Nahm die Kesselplatte von Martin Heinz
Tim Sainburg
Lizenz