Dieses Projekt hat sich auf die Steigerung verschoben (Math/Differenzierung/Autodiff) und dieses Repository wird nicht mehr aktualisiert.
| Zweig | Travis | Appveyor | Codecov.io |
|---|---|---|---|
master | |||
develop |
Autodiff ist eine C ++-C ++-Bibliothek mit Header, die die automatische Differenzierung (Vorwärtsmodus) der mathematischen Funktionen einzelner und mehrerer Variablen erleichtert.
Diese Implementierung basiert auf der Expansion einer Analysefunktion F am Punkt X₀ :
Die wesentliche Idee des Autodiffs ist die Substitution von Zahlen durch Polynome bei der Bewertung von F (x₀) . Durch das Ersetzen der Zahl x₀ durch das Polynom x₀+ε erster Ordnung und die Verwendung desselben Algorithmus zur Berechnung f (x₀+ε) enthält das resultierende Polynom in ε die Ableitungen der Funktion f '(x₀) , f' '(x₀) , f '' '(x₀) , ... innerhalb der Koeffizienten. Jeder Koeffizient entspricht der Ableitung seiner jeweiligen Ordnung, geteilt durch das Faktor der Ordnung.
Angenommen, man möchte die ersten N -Derivate von F bei x₀ berechnen. Ohne Präzisionsverlust für die Berechnung der Derivate können alle Begriffe O (ε n+1 ), die Kräfte von ε größer als n enthalten, verworfen werden. (Dies ist auf die Tatsache zurückzuführen, dass jeder Begriff in einem Polynom nur von den Begriffen gleicher und geringerer Ordnung unter arithmetischen Operationen abhängt.) Nach diesen Kürzungsregeln liefert F eine Polynom-zu-Polynom-Transformation:
Die Fähigkeit von C ++, Operatoren und Funktionen zu überlasten, ermöglicht die Erstellung einer Klasse fvar , die Polynome in ε darstellt. Daher wird der gleiche Algorithmus f, der den numerischen Wert von y₀ = f (x₀) berechnet, wenn es geschrieben wird , um Variablen eines generischen (Template) Typs zu akzeptieren und zurückzugeben ε) . Die Derivate f (n) (x₀) werden dann aus dem Produkt des jeweiligen faktoriellen n gefunden! und Koeffizient y n :

#include <Boost/Math/Differenzierung/autodiff.hpp> #include <iostream> Vorlage <typername t>
T vierte_power (t const & x) {
T x4 = x * x; // RetVal im Operator*() verwendet den Speicher von X4 über NRVO.
x4 *= x4; // Kopien von x4 werden im Operator*= () selbst beim Quadrieren durchgeführt.
Rückgabe x4; // x4 verwendet den Speicher von y in main () über nrvo.} int main () {verwenden namespace boost :: math :: differenzierung;
Unsigned Order = 5; // Ableitung mit höchster Ordnung, die berechnet werden sollen.
auto const x = make_fvar <double, order> (2.0); // Finden Sie Ableitungen bei x = 2.
auto const y = viertes_power (x); für (nicht signiert i = 0; i <= order; ++ i)
std :: cout << "y.derivative (" << i << ") =" << y.derivative (i) << std :: endl; Rückkehr 0;
}/*Ausgabe: y.derivativ (0) = 16y.derivat (1) = 32y.derivat (2) = 48y.derivat (3) = 48y.derivat (4) = 24 Jahre (5) = 0*//Das obige berechnet
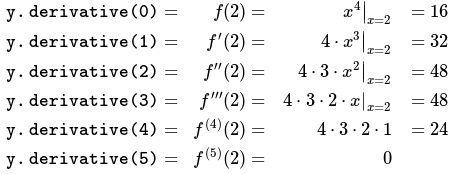
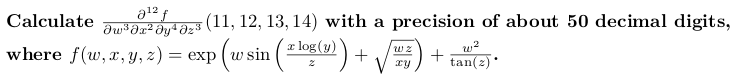
#include <boost/math/differenzierung/autodiff.hpp> #include <boost/multipRecision/cpp_bin_float.hpp> #include <iostream> Verwenden von Namespace Boost :: Math :: Differenzierung; Vorlage <Typename Typname z>
Werben Sie <w, x, y, z> f (const w & w, const x & x, const y & y, const z & z) {Verwenden von Namespace std;
return exp (w * sin (x * log (y) / z) + sqrt (w * z / (x * y))) + w * w / tan (z);
} int main () {use float50 = boost :: multipRecision :: cpp_bin_float_50; stolpexpr nicht signiert nw = 3; // maxe Ableitungsreihenfolge für W.
konstetexpr nicht signiert nx = 2; // maxe Ableitungsreihenfolge für x zu berechnen
konstetexpr unsigned ny = 4; // maximale Ableitungsreihenfolge für y zu berechnen
konstestexpr nicht signiert nz = 3; // maxe Ableitungsreihenfolge für z zur Berechnung für z
// 4 unabhängige Variablen zusammen in ein std :: tupel deklarieren.
auto const variablen = make_ftuple <float50, nw, nx, ny, nz> (11, 12, 13, 14); Auto const & w = std :: Get <0> (Variablen); // bis zu NW -Derivaten bei w = 11
Auto const & x = std :: Get <1> (Variablen); // bis zu NX -Derivaten bei x = 12
Auto const & y = std :: Get <2> (Variablen); // bis zu NY -Derivaten bei y = 13
Auto const & z = std :: Get <3> (Variablen); // bis zu NZ -Derivaten bei z = 14
Auto const v = f (w, x, y, z); // aus mathematischer symbolischer Differenzierung berechnet.
Float50 const Antwort ("1976.319600747797717798881875290418720908121189218755");
std :: cout << std :: setPrecision (std :: numeric_limits <float50> :: digits10)
<< "Mathematica:" << Antwort << 'n' << "Autodiff:" << V.derivative (NW, NX, NY, NZ) << 'N' << std :: setPrecision (3)
<< "Relativer Fehler:" << (V.derivative (NW, NX, NY, NZ) / Antwort - 1) << 'n'; Rückkehr 0;
}/*Ausgabe: Mathematica: 1976.3196007477977177798818752904187209081211892188Autodiff: 1976.3196007477777779881875290418720908121121189218relative #include <Boost/Math/Differenzierung/autodiff.hpp> #include <IoStream> Verwenden von Namespace Boost :: Math :: Constants; Verwenden von Namespace Boost :: Math :: Differenzierung; // Gleichungen und Funktionen/Variablennamen stammen von // https://en.wikipedia.org/wiki/greeks_(finance)#formulas_for_european_option_greeks// Standard Normale kumulative Verteilungsfunktionsablage <ypename x>
X phi (x const & x) {return 0,5 * ERFC (-one_div_root_two <x> () * x);
} Enum -Klasse CP {call, put}; // Null jährliche Dividend -Rendite (q = 0) .Template <Typename Preis, Typname Sigma, TypName Tau, TypEname Rate>
Fördern Sie <Preis, Sigma, Tau, Rate> Black_scholes_Option_price (CP CP, Double K,
Preis const & s,
Sigma Const & Sigma,
Tau const & Tau,
Rate const & r) {namespace std;
auto const d1 = (log (s / k) + (r + sigma * sigma / 2) * tau) / (sigma * sqrt (Tau)); auto const d2 = (log (s / k) + (r - Sigma * Sigma / 2) * tau) / (Sigma * Sqrt (Tau)); Switch (cp) {case cp :: call: return s * phi (d1)-exp (-r * tau) * k * phi (d2); case cp :: put: return exp (-r * tau) * k * Phi (-d2)-s * phi (-d1);
}
} int main () {double const k = 100.0; // Ausübungspreis.
auto const s = make_fvar <double, 2> (105); // Aktienkurs.
double const sigma = 5; // Volatilität.
Doppelkonstant Tau = 30,0 / 365; // Zeit bis zum Ablauf in Jahren. (30 Tage).
double const r = 1,25 / 100; // Zinssatz.
auto const call_price = schwarz_scholes_option_price (cp :: call, k, s, sigma, tau, r); auto const put_price = schwarz_scholes_option_price (cp :: put, k, s, sigma, tau, r);
std :: cout << "Black-Scholes Call price =" << call_price.derivative (0) << 'n' << "Black-Scholes Put price =" << put_price.derivative (0) << 'n' << "call delta =" << call_price.derivative (1) << 'n' << "put delta =" << put_price.derivative (1) << 'n' << "call gamma =" << call_price .Derivativ (2) << 'n' << "put gamma =" << put_price.derivative (2) << 'n'; Rückkehr 0;
}/*Ausgabe: Schwarz-Scholen-Anrufpreis = 56.5136Black-Scholes PREIS = 51.4109CALL Delta = 0,773818 Put Delta = -0.226182Call Gamma = 0,00199852put Gamma = 0,00199852*///////////////0/0//0,0019852put Gamma = 0,00199852*/In Beispiel/Black_Scholes.cpp finden Sie eine größere Liste der automatisch berechneten Option Griechen.
Die obigen Beispiele veranschaulichen einige der Vorteile der Verwendung von Autodiff:
Eliminierung der Code -Redundanz. Die Existenz von n getrennten Funktionen zur Berechnung der Derivate ist eine Form der Code -Redundanz mit allen damit verbundenen Verbindlichkeiten:
Änderungen an einer Funktion erfordern n zusätzliche Änderungen an anderen Funktionen. Überlegen Sie sich im obigen dritten Beispiel, wie viel größer und voneinander abhängig die obige Codebasis wäre, wenn eine separate Funktion für jeden griechischen Wert geschrieben würde.
Die Abhängigkeiten von einer Derivatfunktion für einen anderen Zweck brechen, wenn Änderungen an der ursprünglichen Funktion vorgenommen werden. Was nicht existieren muss, kann nicht brechen.
Code aufblähen, die konzeptionelle Integrität verringern. Die Kontrolle über die Entwicklung des Codes ist einfacher/sicherer, wenn die Codebasis kleiner ist und intuitiv erfasst werden kann.
Genauigkeit von Derivaten über endliche Differenzmethoden. Finite-Differenz-Methoden mit Einzelhandelen enthalten immer eine Δx- freie Variable, die für jede Anwendung sorgfältig ausgewählt werden muss. Wenn Δx zu klein ist, werden numerische Fehler groß. Wenn Δx zu groß ist, werden mathematische Fehler groß. Bei Autodiff gibt es keine freien Variablen, und die Genauigkeit der Antwort ist im Allgemeinen den endlichen Differenzmethoden überlegen, selbst mit der besten Wahl von Δx .
Weitere Details finden Sie im Autodiff -Handbuch.
Unter der Boost -Software -Lizenz verteilt, Version 1.0.
Nur Kopfzeile.
Optimiert für C ++ 17. Kompiliert und wird auch mit C ++ 11, C ++ 14 getestet und C ++ 20 -Standards vorgeschlagen.
Der gesamte Speicher wird auf dem Stapel zugewiesen.
| Name | Zweck |
|---|---|
doc | Dokumentation |
example | Beispiele |
include | Header |
test | Unit -Tests |
Berichtsfehler: Erwähnen Sie unbedingt die Version, die Plattform und den Compiler, die Sie verwenden. Ein kleines kompilierbares Code -Beispiel, um das Problem zu reproduzieren, ist auch immer gut.
Senden Sie Ihre Patches als Pull -Anfragen gegen die Entwicklungszweig. Beachten Sie, dass Sie durch die Übermittlung von Patches Ihre Änderungen im Rahmen der Boost -Software -Lizenz, Version 1.0, lizenzieren.