Zuvor haben wir einige häufig verwendete integrierte Module in Python kennengelernt. In diesem Abschnitt erfahren Sie, wie Sie Module von Drittanbietern installieren.
Bevor wir Module von Drittanbietern installieren, können wir zunächst überprüfen, welche Module von Drittanbietern auf unserem Computer installiert wurden. Geben Sie zunächst die cmd-Schnittstelle und die Verknüpfungseingabemethode ein, drücken Sie win + r in der unteren linken Ecke und geben Sie dann cmd ein Drücken Sie die Eingabetaste, rufen Sie die Seite unten auf und geben Sie dann die anzuzeigende Pip-Liste ein.
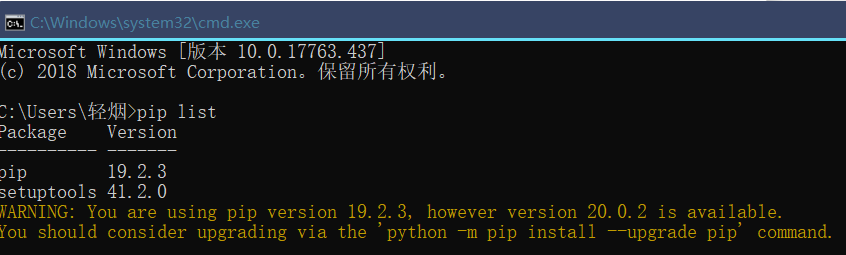
Wir können sehen, dass meine Liste keine redundanten Module von Drittanbietern enthält. Als Nächstes laden wir die Module von Drittanbietern herunter. Der Download-Befehl lautet:
Name des pip-Installationsmoduls
Als nächstes laden wir ein Modul namens numpy herunter, das hauptsächlich für wissenschaftliche Berechnungen verwendet wird.
Beim Herunterladen tritt das im Bild unten gezeigte Problem auf:

Das heißt, meine Pip-Version ist zu niedrig und ich muss die Pip-Version aktualisieren. Dann geben wir python -m pip install --upgrade pip ein, um pip zu aktualisieren.
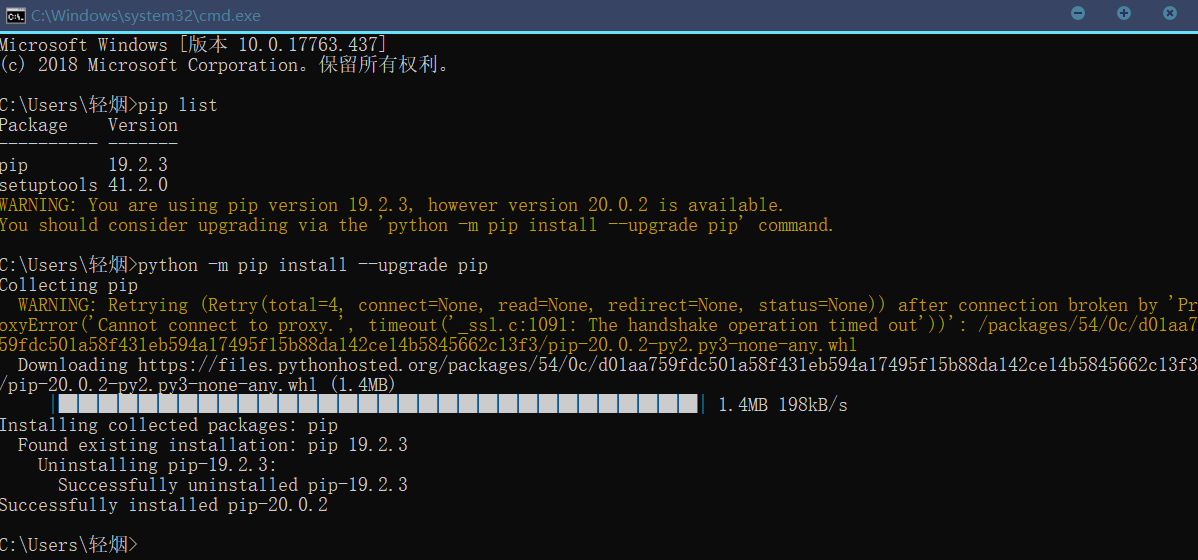
Laden Sie dann das Modul herunter und installieren Sie es.

Dies zeigt, dass die Installation erfolgreich war, und dann führen wir das Numpy-Modul in IDLE ein.

Dies zeigt, dass wir dieses Modul erfolgreich installiert haben und einige Funktionen nutzen können.
Die Installation von Plug-Ins von Drittanbietern in Pycharm ist viel einfacher. Wir klicken direkt auf die Dateitaste in der oberen linken Ecke von Pycharm, suchen und öffnen darin die Einstellungen und rufen die folgende Seite auf:
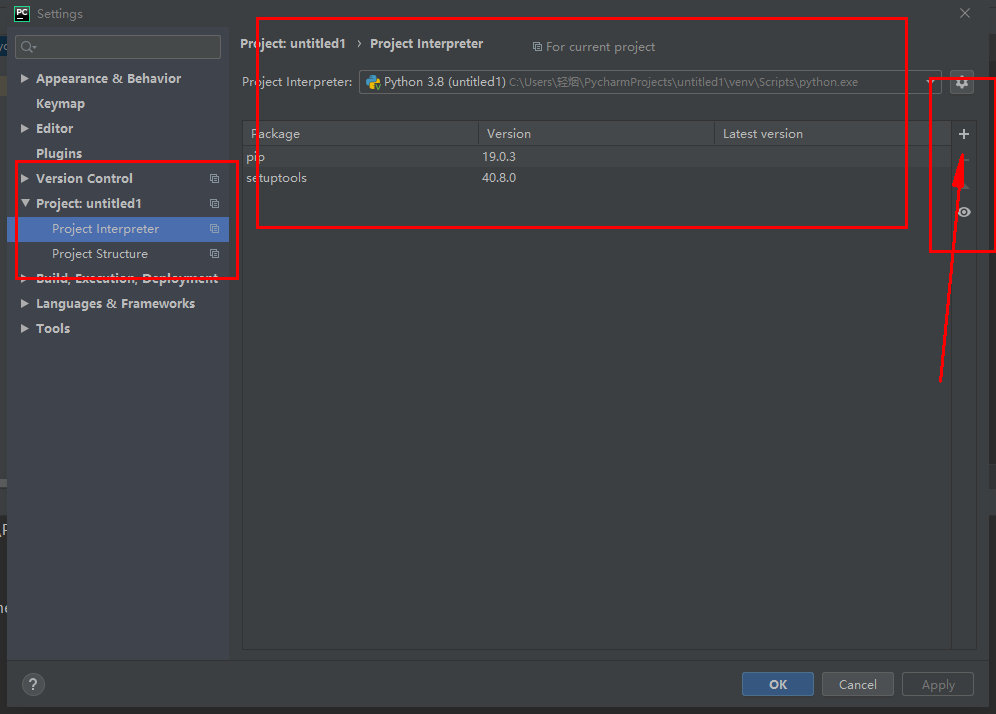
Dann können wir das Modul herunterladen und ganz rechts auf die Schaltfläche „+“ klicken:
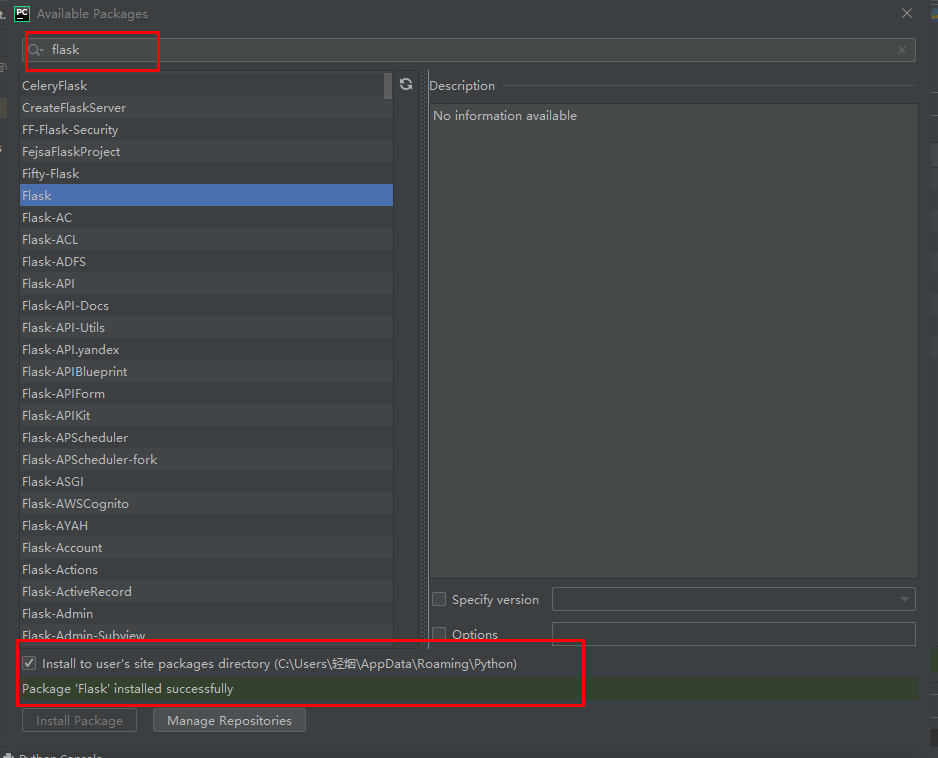
Klicken Sie auf die Schaltfläche unten, bis die Installation erfolgreich ist.
Was die Installation und Verwendung von Drittanbietermodulen betrifft, können Sie feststellen, dass die Verwendung von Pycharm während des Download- und Installationsvorgangs möglicherweise auf verschiedene Fehlermeldungen stößt. Weitere Informationen zur Lösung des Problems finden Sie hier.