In Python gibt es einen speziellen Ausdruck namens Ableitung . Seine Funktion besteht darin, eine Datenstruktur als Eingabe zu verwenden, sie dann zu filtern und zu berechnen und schließlich eine andere Datenstruktur auszugeben. Je nach Datenstruktur kann es in Listenverständnis, Mengenverständnis und Wörterbuchverständnis unterteilt werden. Konzentrieren wir uns zunächst auf die am häufigsten verwendeten Listenverständnisse.
Werfen wir zunächst einen Blick auf das Syntaxformat von Listenverständnissen:
Listenname=[Ausdruck für Variable im Objekt (ifcondition)]
Listenname: der Name der neu generierten Liste.
Ausdruck: Ausdruck.
Variable: Variablenname.
(wenn Bedingung): Wird verwendet, um eine Liste auszuwählen, die den Anforderungen des Objekts entspricht.
Wir gehen von drei Aspekten aus: einer Liste von Werten innerhalb eines bestimmten Bereichs, einer Liste bestimmter Bedingungen und einer Liste von Elementen, die die Bedingungen erfüllen.
Lassen Sie uns zunächst darüber nachdenken, wann wir 10 Zahlen generieren und in einer Liste speichern müssen. Schauen wir uns zunächst die übliche Methode an:
listname=[]foriinrange(10):listname.append(i)print(listname)
Die Ausgabe ist:
[0,1,2,3,4,5,6,7,8,9]
Für die Verwendung eines Listenverständnisses ist nur eine Zeile erforderlich:
Listenname=[iforiinrange(10)]
Die Ausgabe ist:
[0,1,2,3,4,5,6,7,8,9]
Dieser Ansatz vereinfacht unsere Vorgänge beim Definieren von Listen.
Angenommen, wir wissen, dass eine Liste listname = [1,3,5,6,7,9,10,23,26,28,64,98] ist. Wir möchten sie finden und alle darin enthaltenen Zahlen um 5 addieren. Die gewöhnliche Methode:
listname=[1,3,5,6,7,9,10,23,26,28,64,98]foriinrange(len(listname)):listname[i]+=5print(listname)
Die Ausgabe ist:
[6,8,10,11,12,14,15,28,31,33,69,103]
Auch die Verwendung von Listenverständnissen ist sehr prägnant:
Listenname=[1,3,5,6,7,9,10,23,26,28,64,98]Listenname=[i+5foriinlistname]
Ausgabe:
[6,8,10,11,12,14,15,28,31,33,69,103]
Diese Art des Listenverständnisses ist komplexer als die ersten beiden, kann jedoch den Code stärker vereinfachen.
Schauen wir uns das Codeformat anhand eines Beispiels an:
Es ist bekannt, dass eine Liste Listenname = [8,33,53,64,73,95,101,123,126,164,198] ist. Dann müssen wir die Zahlen in der Liste finden, die kleiner und größer als 100 sind, sie dann mit 0,8 multiplizieren und schließlich Bringen Sie sie in die Liste zurück.
Wenn wir die normale Methode verwenden:
listname=[10,20,30,40,60,120,130,140,160,180,200]newlist=[]#Erstellen Sie eine neue Liste zum Speichern foriinrange(len(listname)):#Indexwertdurchlauf iflistname[i]>100:#Suchen Sie eine Zahl größer als 100 listname[ i]*=0,8#Mit 0,8 multiplizieren newlist.append(listname[i])#Zu neuer Liste hinzufügen print(newlist)
Die Ausgabe ist:
[96,0,104,0,112,0,128,0,144,0,160,0]
Verwenden Sie Listenverständnisse:
listname=[10,20,30,40,60,120,130,140,160,180,200]newlist=[i*0.8foriinlistnameifi>100]print(newlist)
Ausgabeergebnis:
[96,0,104,0,112,0,128,0,144,0,160,0]
Lassen Sie es uns anhand der grammatikalischen Struktur dieses Beispiels analysieren:
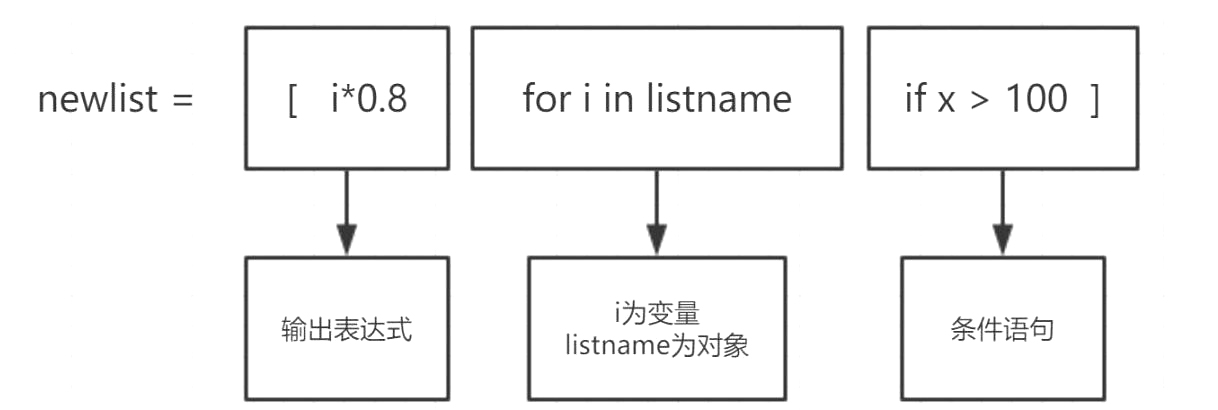
Wir können diese Methode verwenden, wenn wir komplexe Listenverständnisse verwenden. Es kann verstanden werden, dass wir zuerst die Elemente aus dem Objekt auswählen, die die Bedingungen erfüllen, dann den Ausgabeausdruck verarbeiten und sie schließlich in der Liste speichern neue Liste.
Hier sind einige Beispielfragen, die Sie ausprobieren können.
1. Listen Sie [1,2,13,22,25] auf. Verwenden Sie bitte das Listenverständnis, um Zahlen größer als 10 zu extrahieren, jede Zahl zu quadrieren und schließlich auszugeben.
Das laufende Ergebnis ist:
[169.484.625]
Der Code lautet wie folgt: Sie können zuerst versuchen, die Referenzantwort zu vervollständigen.
list=[1,2,13,22,25]newlist=[i*iforiinlistifi>10]print(newlist)
2. Verwenden Sie das Listenverständnis, um alle ungeraden Zahlen in der Liste zu finden und eine neue Liste zu erstellen, list= [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
Der Code lautet wie folgt:
list=[1,2,3,4,5,6,7,8,9,10]newlist=[iforiinlistifi%2==1]print(newlist)
Die Ausgabe ist:
[1,3,5,7,9]