Das Problem der beschäftigten Biber, ein seit vierzig Jahren bestehendes Informatikproblem, wurde endlich von einer Gruppe Amateuren gelöst! Diese bahnbrechende Entwicklung schockierte nicht nur die akademische Gemeinschaft, sondern wurde auch vom berühmten Mathematiker Terence Tao anerkannt und als die wichtigste Entwicklung auf diesem Gebiet seit 1983 gefeiert. Mithilfe des Coq-Beweisassistenten konnten sie erfolgreich verifizieren, dass der Wert der fünften Busy-Beaver-Zahl BB(5) 47.176.870 beträgt. Dies demonstriert das große Potenzial softwaregestützter Beweise bei der Lösung komplexer mathematischer Probleme und liefert uns auch Einblicke in das Verhalten von Turing-Maschinen und neue Perspektiven aufhalten.
In einem mysteriösen Bereich der Informatik wurde kürzlich ein vierzig Jahre altes Problem namens „Busy Beaver Problem“ von einer Gruppe Amateuren erfolgreich gelöst. Diese Leistung sorgte nicht nur in der akademischen Welt für Aufsehen, sondern wurde auch vom berühmten Mathematiker Terence Tao gewürdigt, der die Nachricht in den sozialen Medien verbreitete und die Bedeutung von Beweisassistenten in der mathematischen Forschung hervorhob.
Auch der Informatiker Scott Aaronson lobte diese Entdeckung und hielt sie für die wichtigste Entwicklung in der Forschung zu den Funktionen von Bibern seit 1983. Diese Leistung markiert ein tiefes Verständnis der Grenzen der Computertheorie und zeigt das Potenzial softwaregestützter Beweise bei der Lösung komplexer mathematischer Probleme.
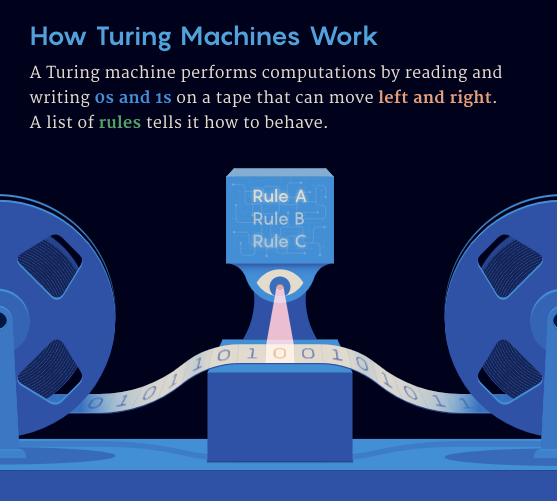
Das Problem der beschäftigten Biber entstand vor mehr als 40 Jahren in Dortmund, als Informatiker versuchten, eine bestimmte Turing-Maschine zu finden, die die meisten Einsen schreiben konnte, bevor sie anhielt. Eine Turing-Maschine ist ein abstraktes Rechenmodell, das 1936 von Alan Turing vorgeschlagen wurde und Berechnungen auf einem unendlich langen Magnetband durch Lesen und Schreiben von Nullen und Einsen durchführt.

Nachdem im Jahr 1974 die Zahl der vierten fleißigen Biber ermittelt worden war, wurde die Frage nach dem fünften Biber zu einer offenen Frage. Jetzt hat eine Online-Community von mehr als 20 Mitwirkenden aus der ganzen Welt mithilfe der Beweisassistentensoftware Coq erfolgreich überprüft, dass die fünfte Busy Beaver-Zahl BB(5) einen Wert von 47.176.870 hat.
Diese Leistung begeisterte nicht nur die Community, sondern weckte auch das Erstaunen des Informatikers Damien Woods, der den Fortschritt mit der Geschwindigkeit von Usain Bolt verglich. Obwohl die Lösung dieses Problems möglicherweise nicht direkt auf andere Bereiche der Informatik anwendbar ist, ist dieser Kampf gegen die mathematische Unmöglichkeit für die Teilnehmer die größte Belohnung an sich.
Der Kern des Busy-Beaver-Problems liegt im Verständnis des Verhaltens von Turing-Maschinen, insbesondere ihrer Leistung bei Stoppproblemen. Das Verhalten einer Turingmaschine wird durch ein Regelwerk definiert, das man sich als Tabelle vorstellen kann. Jede Regel gibt eine Aktion an, die ausgeführt werden soll, wenn der Lese-/Schreibkopf in einem bestimmten Zustand auf eine 0 oder eine 1 trifft.
Obwohl Turing-Maschinen in Endlosschleifen stecken bleiben können, ist die Feststellung, ob sie jemals aufhören zu laufen, ein bekanntermaßen ungelöstes Problem. Der Mathematiker Tibor Radó war mit dieser Schlussfolgerung nicht zufrieden und erfand daher das „Busy-Beaver-Spiel“, um die Natur des Halteproblems zu erforschen, indem er Turing-Maschinen nach der Anzahl ihrer Regeln gruppierte.
Frühe Forscher wie Allen Brady untersuchten dieses Problem, indem sie Programme schrieben, um das Verhalten von Turing-Maschinen zu simulieren. Seine Arbeit und die Entdeckungen anderer Forscher legten den Grundstein für spätere Entdecker.
Bis 2022 startete der Doktorand Tristan Stérin die Busy Beaver Challenge, ein Online-Kooperationsprojekt mit dem Ziel, BB(5) fertigzustellen. Durch innovative Methoden und die Hilfe des Coq Proof Assistant gelang es dem Team schließlich, den fünften fleißigen Biber zu finden.
Diese Leistung ist nicht nur eine Herausforderung an die Unmöglichkeit der Mathematik, sondern auch eine Erkundung der Grenzen der Informatik. Nachdem BB(5) bestätigt wurde, entwerfen die Forscher eine wissenschaftliche Arbeit, die eine für Menschen lesbare Version sein wird, die den Coq-Beweis ergänzt. Gleichzeitig denken sie auch darüber nach, ob die Erkundung von BB(6) das nächste Ziel sein wird.
Referenz: https://www.quantamagazine.org/amateur-mathematicians-find-fifth-busy-beaver-turing-machine-20240702/
Die Lösung des Problems der beschäftigten Biber ist nicht nur ein großer Durchbruch auf dem Gebiet der Mathematik, sondern liefert auch neue Richtungen und Ideen für die zukünftige computertheoretische Forschung. Dieser Erfolg ermutigt mehr Menschen, sich an der Forschung in Mathematik und Informatik zu beteiligen und gemeinsam unbekannte Gebiete zu erkunden.