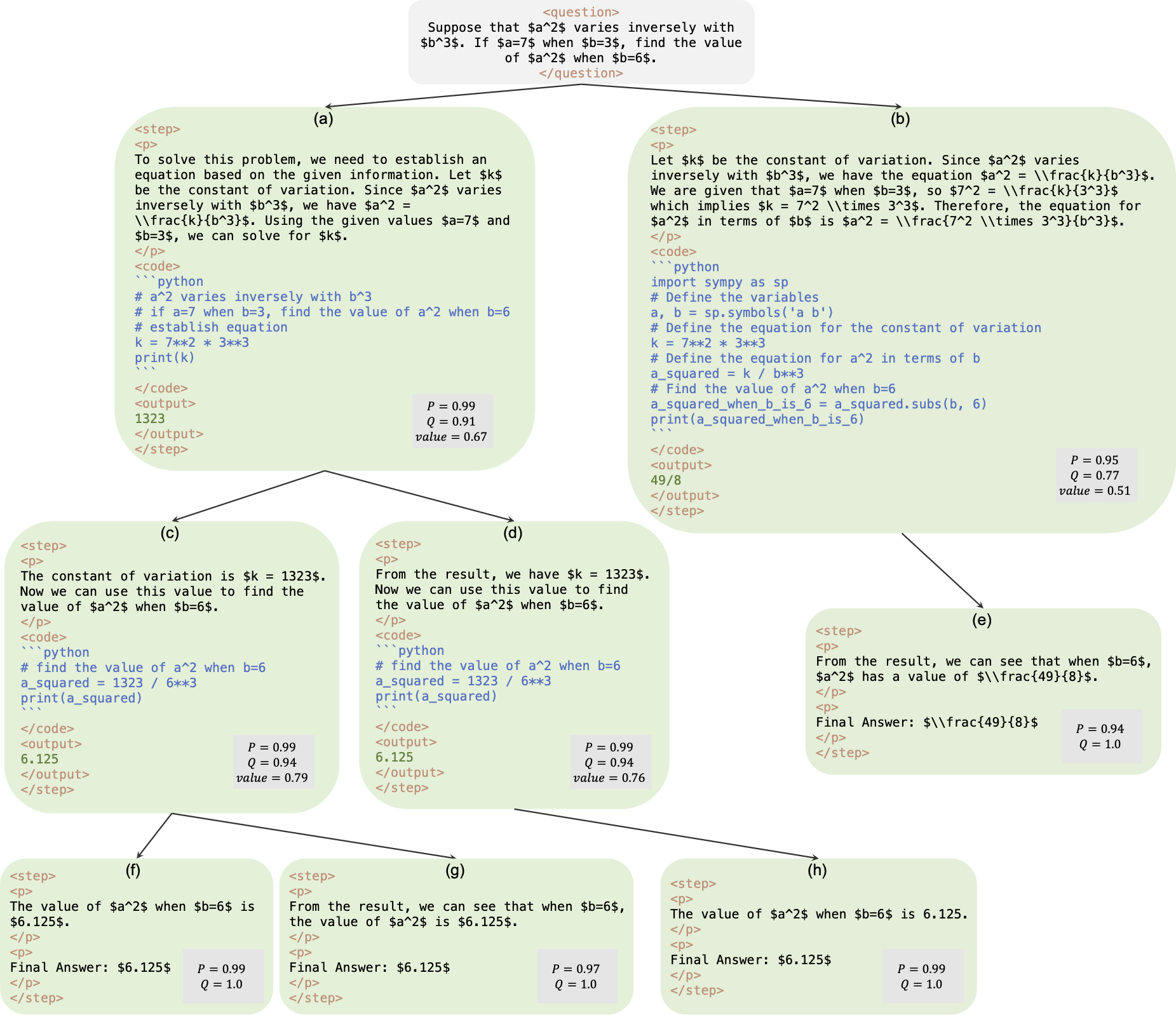
This is the official repository for paper AlphaMath Almost Zero: process Supervision without process. The code is extracted from our internal corporate codebase. As a result, there may be slight differences when reproducing the numbers reported in our paper, but they should be very close. Our approach involves training the policy and value models using only the mathematical reasoning derived from the Monte Carlo Tree Search (MCTS) framework, eliminating the need for GPT-4 or human annotations. This is an illustration of training instance generated by MCTS in round 3.
Checkpoint: AlphaMath-7B round 3 ? / AlphaMath-7B round 3 ?
Dataset: AlphaMath-Round3-Trainset ? The solution process of the training data is automatically generated based on MCTS and checkpoint in round 2. Both positive and negative examples are included for training the policy and value models.
Training Code: Due to policy, we can only release the implementation details of some key functions, which should basically be modified in your own training code.
| Inference Method | Accuracy | avg. time (s) per q | avg. steps | # sols |
|---|---|---|---|---|
| Greedy | 53.62 | 1.6 | 3.1 | 1 |
| Maj@5 | 61.84 | 2.9 | 2.9 | 5 |
| Step-level Beam (1,5) | 62.32 | 3.1 | 3.0 | top-1 |
| 5 runs + Maj@5 | 67.04 | x5 | x1 | 5 top-1 |
| Step-level Beam (2,5) | 64.66 | 2.4 | 2.4 | top-1 |
| Step-level Beam (3,5) | 65.74 | 2.3 | 2.2 | top-1 |
| Step-level Beam (5,5) | 65.98 | 4.7 | 2.3 | top-1 |
| 1 run + Maj@5 | 66.54 | x1 | x1 | top-5 |
| 5 runs + Maj@5 | 69.94 | x5 | x1 | 5 top-1 |
| MCTS (N=40) | 64.02 | 10.1 | 3.8 | top-1 |
+ Maj@5 requires to run 5 times, which encourage diversity.+ Maj@5 directly uses the 5 candidates, which lack of diversity.| temperature | 0.6 | 1.0 |
|---|---|---|
| Step-level Beam (1,5) | 62.32 | 62.76 |
| Step-level Beam (2,5) | 64.66 | 65.60 |
| Step-level Beam (3,5) | 65.74 | 66.28 |
| Step-level Beam (5,5) | 65.98 | 66.38 |
For step-level beam search, setting temperature=1.0 may achieve slightly better results.
requirements.txt
pip install -r requirements.txt
Or simply follow the cmds
> git clone https://github.com/MARIO-Math-Reasoning/Super_MARIO.git
> git clone https://github.com/MARIO-Math-Reasoning/MARIO_EVAL.git
> git clone https://github.com/MARIO-Math-Reasoning/vllm.git
> cd Super_MARIO && pip install -r requirements.txt && cd ..
> cd MARIO_EVAL/latex2sympy && pip install . && cd ..
> pip install -e .
> cd ../vllm
> pip install -e .scripts/save_value_head.py to add the value head to the LLM.You can run either of the following two cmds. There may be slightly difference of accuracy between the two. In our machine, the first got 53.4% and the second got 53.62%.
python react_batch_demo.py
--custom_cfg configs/react_sft.yaml
--qaf ../MARIO_EVAL/data/math_testset_annotation.json
or
# use step_beam (1, 1) without value func
python solver_demo.py
--custom_cfg configs/sbs_greedy.yaml
--qaf ../MARIO_EVAL/data/math_testset_annotation.json
In our machine, on MATH testset, the following cmd with config B1=1, B2=5 can achieve ~62%, and the one with config B1=3, B2=5 can reach ~65%.
python solver_demo.py
--custom_cfg configs/sbs_sft.yaml
--qaf ../MARIO_EVAL/data/math_testset_annotation.json
Calculate the accuracy
python eval_output_jsonl.py
--res_file <the saved tree jsonl file by solver_demo.py>
The ground_truth (the final answer, not the solution process) must be provided in qaf json or jsonl file (example format can refer to ../MARIO_EVAL/data/math_testset_annotation.json).
round 1
# Checkpoint Initialization is required by adding value head
python solver_demo.py
--custom_cfg configs/mcts_round1.yaml
--qaf /path/to/training/data
round > 1, after SFT
python solver_demo.py
--custom_cfg configs/mcts_sft_round.yaml
--qaf /path/to/training/data
Only question will be used for solution generation, but the ground_truth will be used for calculating the accuracy.
python solver_demo.py
--custom_cfg configs/mcts_sft.yaml
--qaf ../MARIO_EVAL/data/math_testset_annotation.json
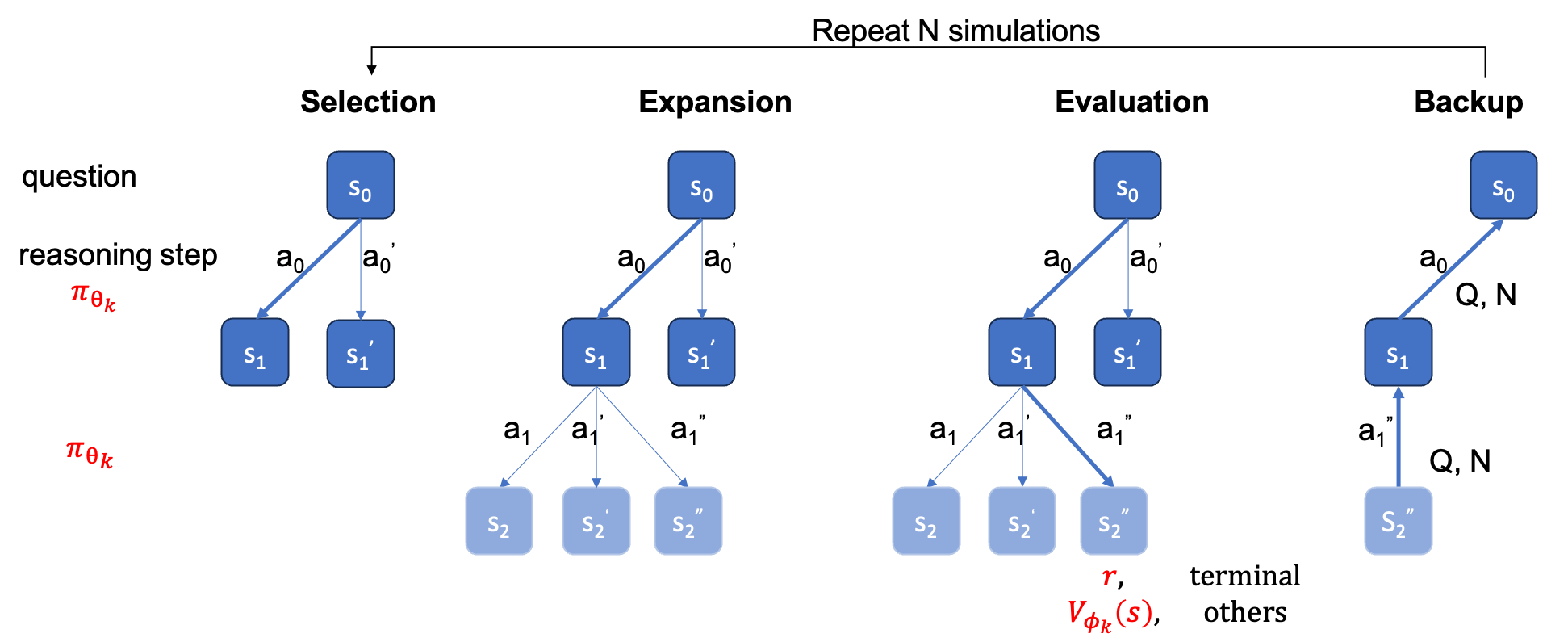
Different from step-level beam search, you need first to build a complete tree, then you should run the MCTS offline then calculate the accuracy.
python offline_inference.py
--custom_cfg configs/offline_inference.yaml
--tree_jsonl <the saved tree jsonl file by solver_demo.py>
Note: this evaluation script can also be run with saved tree by step-level beam search, and the accuracy should remain the same.
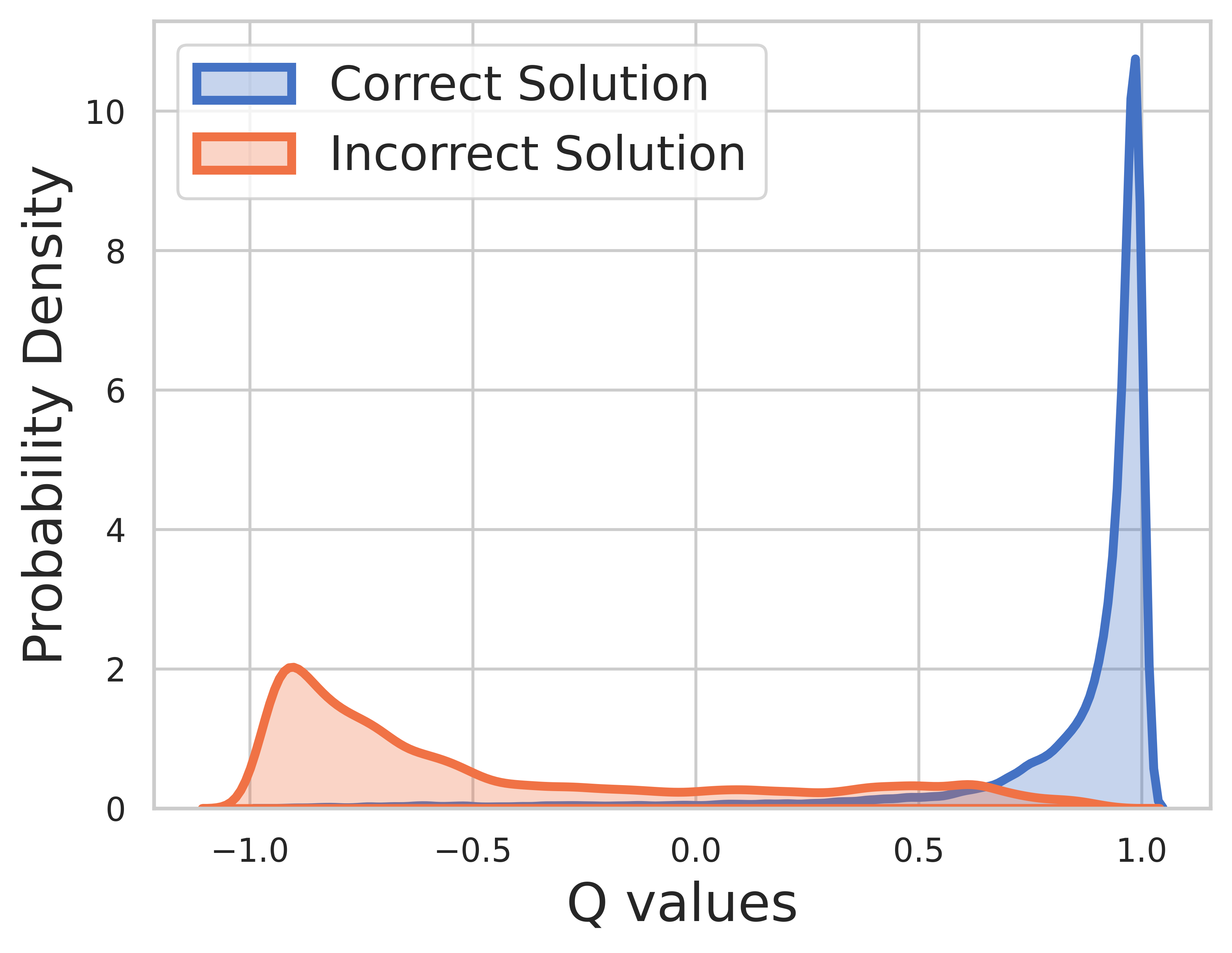
Because ground truth is known for training data, the value of final step is reward and Q-value can converge very well.
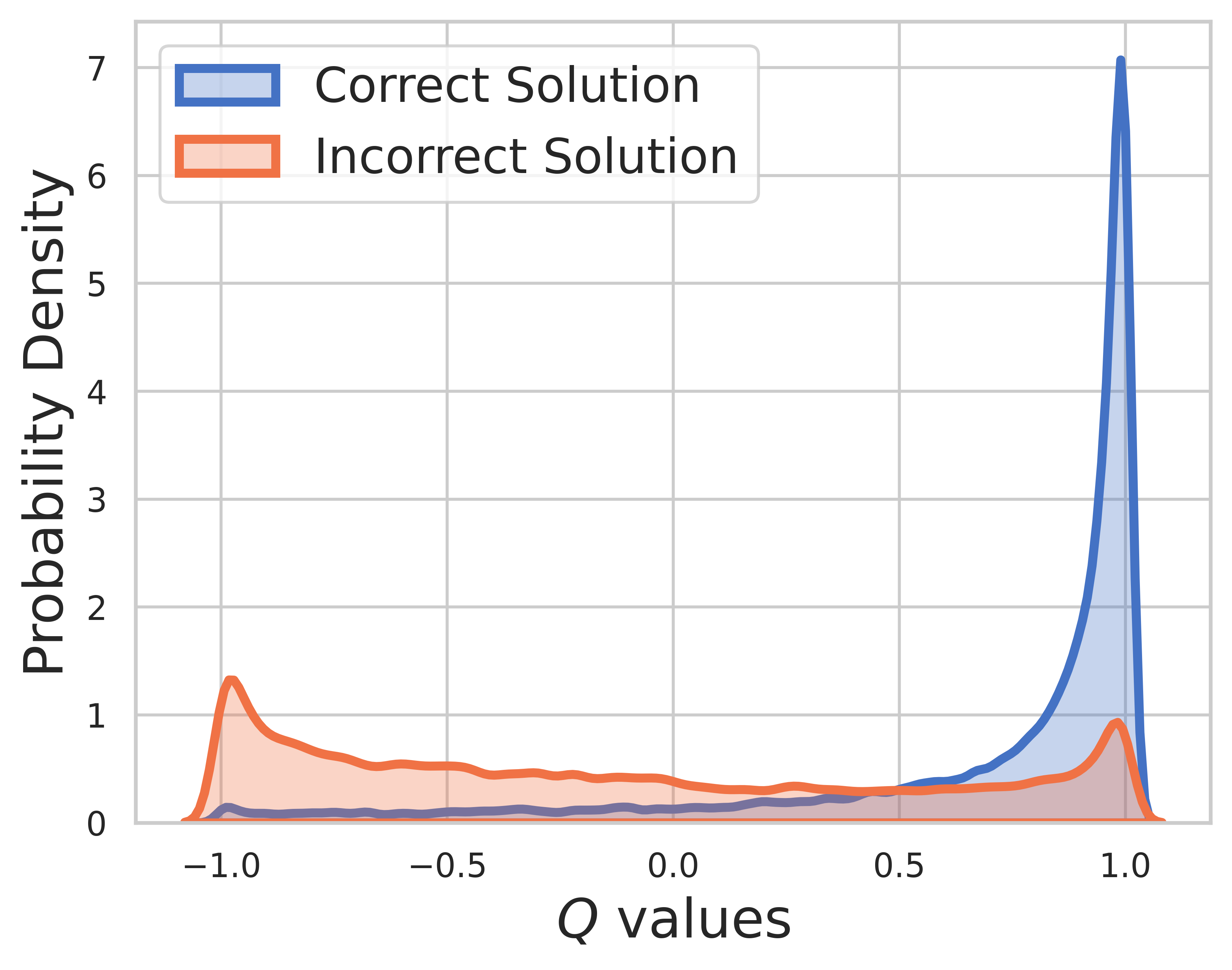
On test set, the ground truth is unknown, so the Q-value distribution includes both intermediate and final steps. From this figure, we can find
SVPO by MCTS
@misc{chen2024steplevelvaluepreferenceoptimization,
title={Step-level Value Preference Optimization for Mathematical Reasoning},
author={Guoxin Chen and Minpeng Liao and Chengxi Li and Kai Fan},
year={2024},
eprint={2406.10858},
archivePrefix={arXiv},
primaryClass={cs.CL},
url={https://arxiv.org/abs/2406.10858},
}
MCTS version
@misc{chen2024alphamathzeroprocesssupervision,
title={AlphaMath Almost Zero: process Supervision without process},
author={Guoxin Chen and Minpeng Liao and Chengxi Li and Kai Fan},
year={2024},
eprint={2405.03553},
archivePrefix={arXiv},
primaryClass={cs.CL},
url={https://arxiv.org/abs/2405.03553},
}
Evaluation toolkit
@misc{zhang2024marioevalevaluatemath,
title={MARIO Eval: Evaluate Your Math LLM with your Math LLM--A mathematical dataset evaluation toolkit},
author={Boning Zhang and Chengxi Li and Kai Fan},
year={2024},
eprint={2404.13925},
archivePrefix={arXiv},
primaryClass={cs.CL},
url={https://arxiv.org/abs/2404.13925},
}
OVM (Outcome Value Model) version
@misc{liao2024mariomathreasoningcode,
title={MARIO: MAth Reasoning with code Interpreter Output -- A Reproducible Pipeline},
author={Minpeng Liao and Wei Luo and Chengxi Li and Jing Wu and Kai Fan},
year={2024},
eprint={2401.08190},
archivePrefix={arXiv},
primaryClass={cs.CL},
url={https://arxiv.org/abs/2401.08190},
}