Bosonic is a library developed for the simulation of photonic systems whose inputs are indistinguishable bosons (in the case of the authors' interest, photons). In particular, it focuses on the rapid computation of the multi-particle transfer functions for these systems and supports computation of the gradient of a cost function with respect to the system parameters. It was originally developed for the devleopment of our Quantum Optical Neural Networks [1] and contains specialized functionality for their simulation and optimization.
Key focuses of this library were two-fold:
The core motivation for this package was the rapid computation of the multi-particle unitary transform as a function of the single particle unitary and the number of bosonic inputs. That is, if we have a four dimensional unitary U, and we know there are 3 photons at the input, we want to know the transformation over the
This is supported by the function bosonic.aa_phi, which is named after Aaronson and Arkhipov, who specified the form of this function that we use as their Φ(U) function in [2]. For example, we can demonstrate the famous Hong-Ou-Mandel effect with a beamsplitter:
>>> import bosonic as b
>>> import numpy as np
>>> U = np.array([[1, 1], [1, -1]], dtype=complex) / np.sqrt(2)
>>> phiU = b.aa_phi(U, 2)
>>> print(phiU)
[[ 0.5 +0.j 0.70710678+0.j 0.5 +0.j]
[ 0.70710678+0.j 0. +0.j -0.70710678+0.j]
[ 0.5 +0.j -0.70710678+0.j 0.5 +0.j]]
>>> print(b.fock.basis(2, 2))
[[2, 0], [1, 1], [0, 2]]
>>> input = np.array([[0], [1], [0]], dtype=complex)
>>> phiU = b.aa_phi(U, 2)
>>> print(phiU.dot(input))
[[ 0.70710678+0.j]
[ 0. +0.j]
[-0.70710678+0.j]]
>>> print(np.abs(phiU.dot(input))**2)
[[0.5]
[0. ]
[0.5]]Here, we build the unitary corresponding to a 50/50 beamsplitter in U. As shown the line after we print phiU, the basis here is [2, 0], [1, 1], and [0, 2]. So the state corresponding to one photon incident at each of the inputs is [0, 1, 0]. In the final line, two lines, we see that the output is an equal superposition over two photons at one output and two photons at the other, with no probability of the photons leaving by different ports.
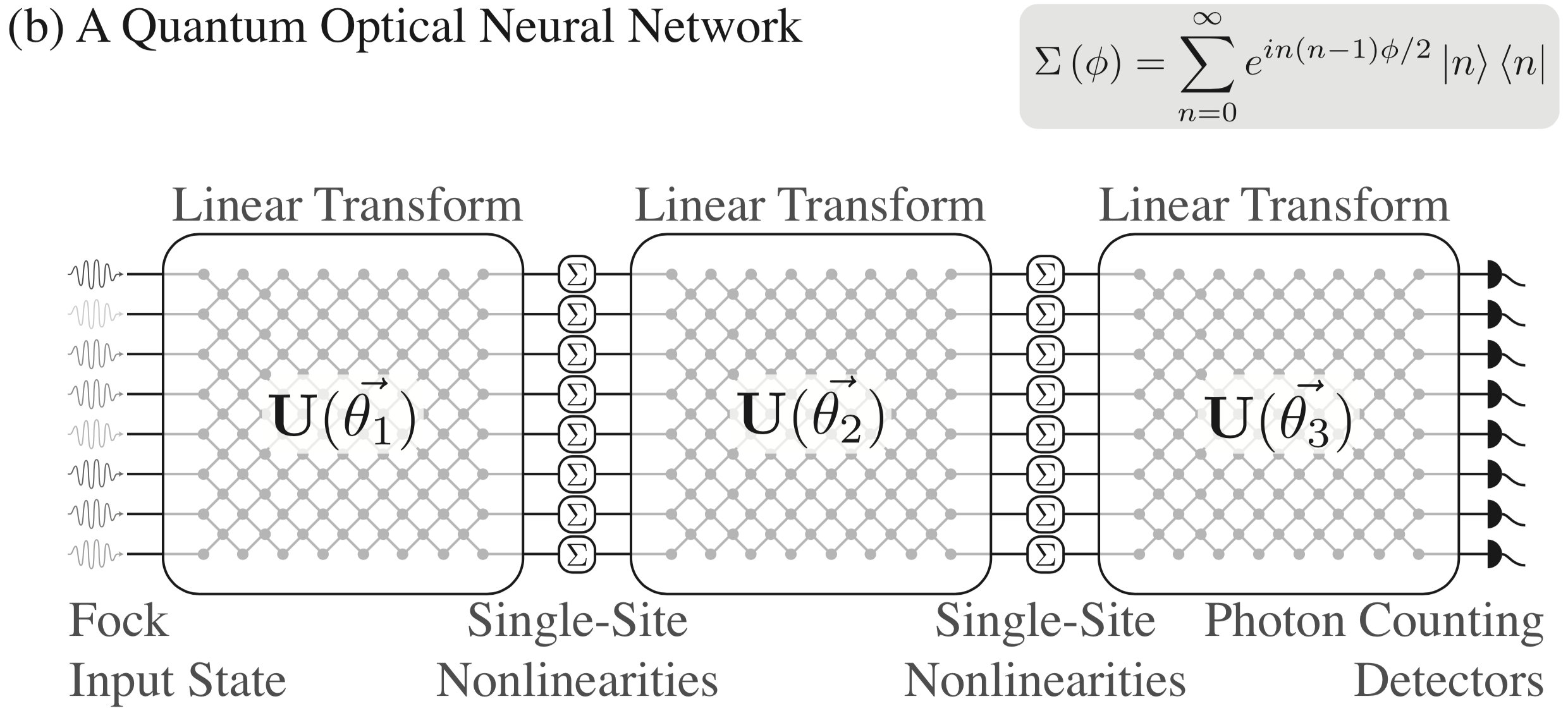
As described in [1], we've developed a proposed architecture for quantum optical neural networks that involves tiling arbitrary unitary transformations with single-site nonlinearities. See the paper for more details, but here's a visual summary of the architecture:
Cloning this repository is currently the only way to get bosonic on your system. Before doing that, you'll need the python package Cython installed, to build bosonic properly. Something like this should work on linux (using your preferred python package manager instead of pip, if desired):
$ pip install Cython
$ git clone [email protected]:steinbrecher/bosonic.git
$ cd bosonic
$ pip install .On Mac, you'll need gcc from homebrew and libopenmp as well:
$ brew install gcc
$ brew install libomp
$ pip install Cython
$ git clone [email protected]:steinbrecher/bosonic.git
$ cd bosonic
$ CC=gcc-8 pip install .You should then be able to test that bosonic is installed correctly by running
$ python setup.py test[1] Steinbrecher, G. R., Olson, J. P., Englund, D., & Carolan, J. (2018). Quantum optical neural networks. arXiv preprint arXiv:1808.10047. https://arxiv.org/abs/1808.10047
[2] Aaronson, Scott, and Alex Arkhipov. "The computational complexity of linear optics." Proceedings of the forty-third annual ACM symposium on Theory of computing. ACM, 2011. https://arxiv.org/pdf/1011.3245.pdf