Home | Installation | Documentation | Tutorial | Developers
rodeo is a fast Python library that uses probabilistic numerics to solve ordinary differential equations (ODEs). That is, most ODE solvers (such as Euler's method) produce a deterministic approximation to the ODE on a grid of step size
rodeo provides a lightweight and extensible family of approximations to a nonlinear Bayesian filtering paradigm common to many probabilistic solvers (Tronarp et al (2018)). This begins by putting a Gaussian process prior on the ODE solution, and updating it sequentially as the solver steps through the grid. rodeo is built on jax which allows for just-in-time compilation and auto-differentiation. The API of jax is almost equivalent to that of numpy.
rodeo provides two main tools: one for approximating the ODE solution and the other for parameter inference. For the former we provide:
solve: Implementation of a probabilistic ODE solver which uses a nonlinear Bayesian filtering paradigm.For the latter we provide the likelihood approximation methods:
basic: Implementation of a basic likelihood approximation method (details can be found in Wu and Lysy (2023)).fenrir: Implementation of Fenrir (Tronarp et al (2022)).marginal_mcmc: MCMC implementation of Chkrebtii's method (Chkrebtii et al (2016)).dalton: Implementation of our data-adaptive ODE likelihood approximation (Wu and Lysy (2023)).Detailed examples for their usage can be found in the Documentation section. Please note that this is the jax-only version of rodeo. For the legacy versions using various other backends please see here.
Download the repo from GitHub and then install with the setup.cfg script:
git clone https://github.com/mlysy/rodeo.git
cd rodeo
pip install .Please first go to readthedocs to see the rendered documentation for the following examples.
A quickstart tutorial on solving a simple ODE problem.
An example for solving a higher-ordered ODE.
An example for solving a difficult chaotic ODE.
An example of a parameter inference problem where we use the Laplace approximation.
In this walkthrough, we show both how to solve an ODE with our probabilistic solver and conduct parameter inference. We will first illustrate the set-up for solving the ODE. To that end, let's consider the following first ordered ODE example (FitzHugh-Nagumo model),
where the solution
Following the notation of (Wu and Lysy (2023)), we have
for
import jax
import jax.numpy as jnp
import rodeo
def fitz_fun(X, t, **params):
"FitzHugh-Nagumo ODE in rodeo format."
a, b, c = params["theta"]
V, R = X[:, 0]
return jnp.array(
[[c * (V - V * V * V / 3 + R)],
[-1 / c * (V - a + b * R)]]
)
def fitz_init(x0, theta):
"FitzHugh-Nagumo initial values in rodeo format."
x0 = x0[:, None]
return jnp.hstack([
x0,
fitz_fun(X=x0, t=0., theta=theta),
jnp.zeros_like(x0)
])
W = jnp.array([[[0., 1., 0.]], [[0., 1., 0.]]]) # LHS matrix of ODE
x0 = jnp.array([-1., 1.]) # initial value for the ODE-IVP
theta = jnp.array([.2, .2, 3]) # ODE parameters
X0 = fitz_init(x0, theta) # initial value in rodeo format
# Time interval on which a solution is sought.
t_min = 0.
t_max = 40.
# --- Define the prior process -------------------------------------------
n_vars = 2 # number of variables in the ODE
n_deriv = 3 # max number of derivatives
sigma = jnp.array([.1] * n_vars) # IBM process scale factor
# --- data simulation ------------------------------------------------------
n_steps = 800 # number of evaluations steps
dt = (t_max - t_min) / n_steps # step size
# generate the Kalman parameters corresponding to the prior
prior_Q, prior_R = rodeo.prior.ibm_init(
dt=dt_sim,
n_deriv=n_deriv,
sigma=sigma
)
# Produce a Pseudo-RNG key
key = jax.random.PRNGKey(0)
Xt, _ = rodeo.solve_mv(
key=key,
# define ode
ode_fun=fitz_fun,
ode_weight=W,
ode_init=X0,
t_min=t_min,
t_max=t_max,
theta=theta, # ODE parameters added here
# solver parameters
n_steps=n_steps,
interrogate=rodeo.interrogate.interrogate_kramer,
prior_weight=prior_Q,
prior_var=prior_R
)We compare the solution from the solver to the deterministic solution provided by odeint in the scipy library.
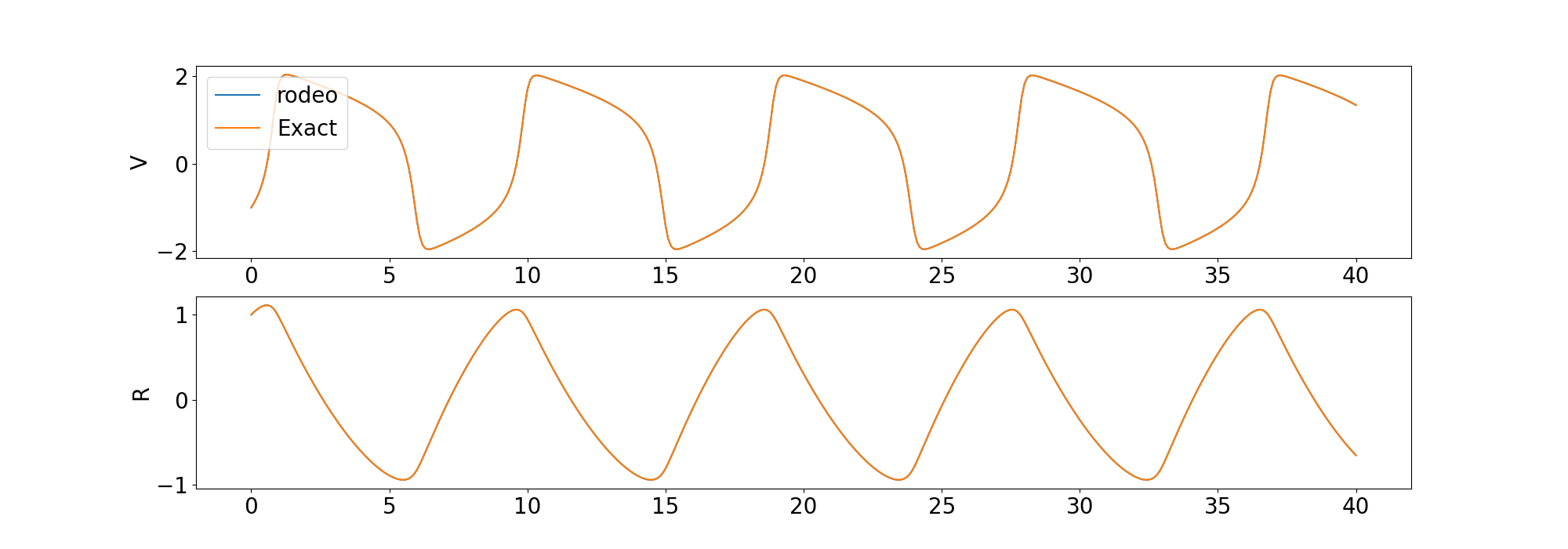
We also include examples for solving a higher-ordered ODE and a chaotic ODE.
We now move to the parameter inference problem. rodeo contains several likelihood approximation methods summarized in the Description section.
Here, we will use the basic likelihood approximation method. Suppose observations are simulated via the model
where basic likelihood approximation for
def fitz_logprior(upars):
"Logprior on unconstrained model parameters."
n_theta = 5 # number of ODE + IV parameters
lpi = jax.scipy.stats.norm.logpdf(
x=upars[:n_theta],
loc=0.,
scale=10.
)
return jnp.sum(lpi)
def fitz_loglik(obs_data, ode_data, **params):
"""
Loglikelihood for measurement model.
Args:
obs_data (ndarray(n_obs, n_vars)): Observations data.
ode_data (ndarray(n_obs, n_vars, n_deriv)): ODE solution.
"""
ll = jax.scipy.stats.norm.logpdf(
x=obs_data,
loc=ode_data[:, :, 0],
scale=0.005
)
return jnp.sum(ll)
def constrain_pars(upars, dt):
"""
Convert unconstrained optimization parameters into rodeo inputs.
Args:
upars : Parameters vector on unconstrainted scale.
dt : Discretization grid size.
Returns:
tuple with elements:
- theta : ODE parameters.
- X0 : Initial values in rodeo format.
- Q, R : Prior matrices.
"""
theta = jnp.exp(upars[:3])
x0 = upars[3:5]
X0 = fitz_init(x0, theta)
sigma = upars[5:]
Q, R = rodeo.prior.ibm_init(
dt=dt,
n_deriv=n_deriv,
sigma=sigma
)
return theta, X0, Q, R
def neglogpost_basic(upars):
"Negative logposterior for basic approximation."
# solve ODE
theta, X0, prior_Q, prior_R = constrain_pars(upars, dt_sim)
# basic loglikelihood
ll = rodeo.inference.basic(
key=key,
# ode specification
ode_fun=fitz_fun,
ode_weight=W,
ode_init=X0,
t_min=t_min,
t_max=t_max,
theta=theta,
# solver parameters
n_steps=n_steps,
interrogate=rodeo.interrogate.interrogate_kramer,
prior_weight=prior_Q,
prior_var=prior_R,
# observations
obs_data=obs_data,
obs_times=obs_times,
obs_loglik=fitz_loglik
)
return -(ll + fitz_logprior(upars))This is a basic example to demonstrate usage. We suggest more sophisticated likelihood approximations which propagate the solution uncertainty to the likelihood approximation such as fenrir, marginal_mcmc and dalton. Please refer to the parameter inference tutorial for more details.
Here are some results produced by various likelihood approximations found in rodeo from /examples/:
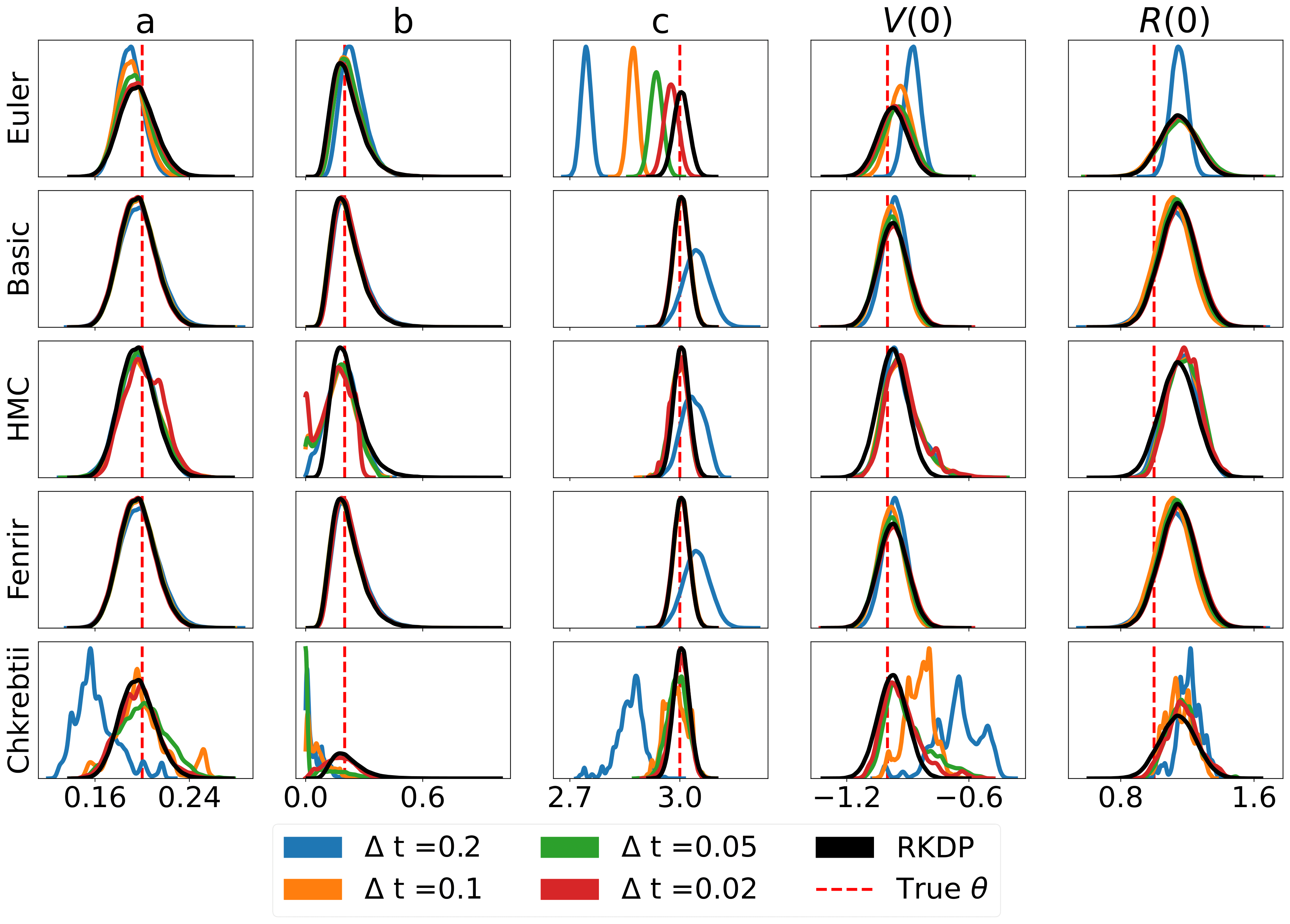
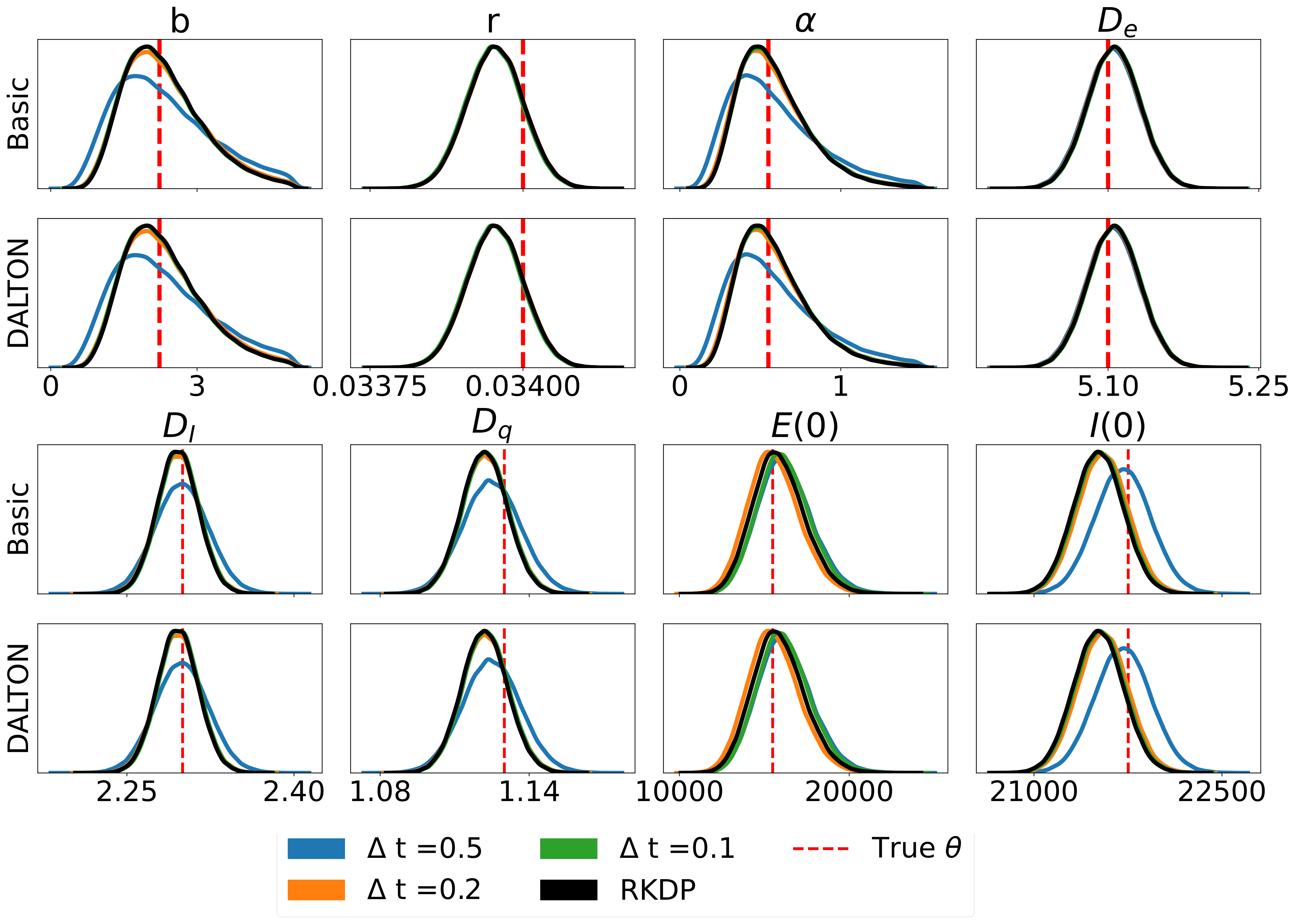
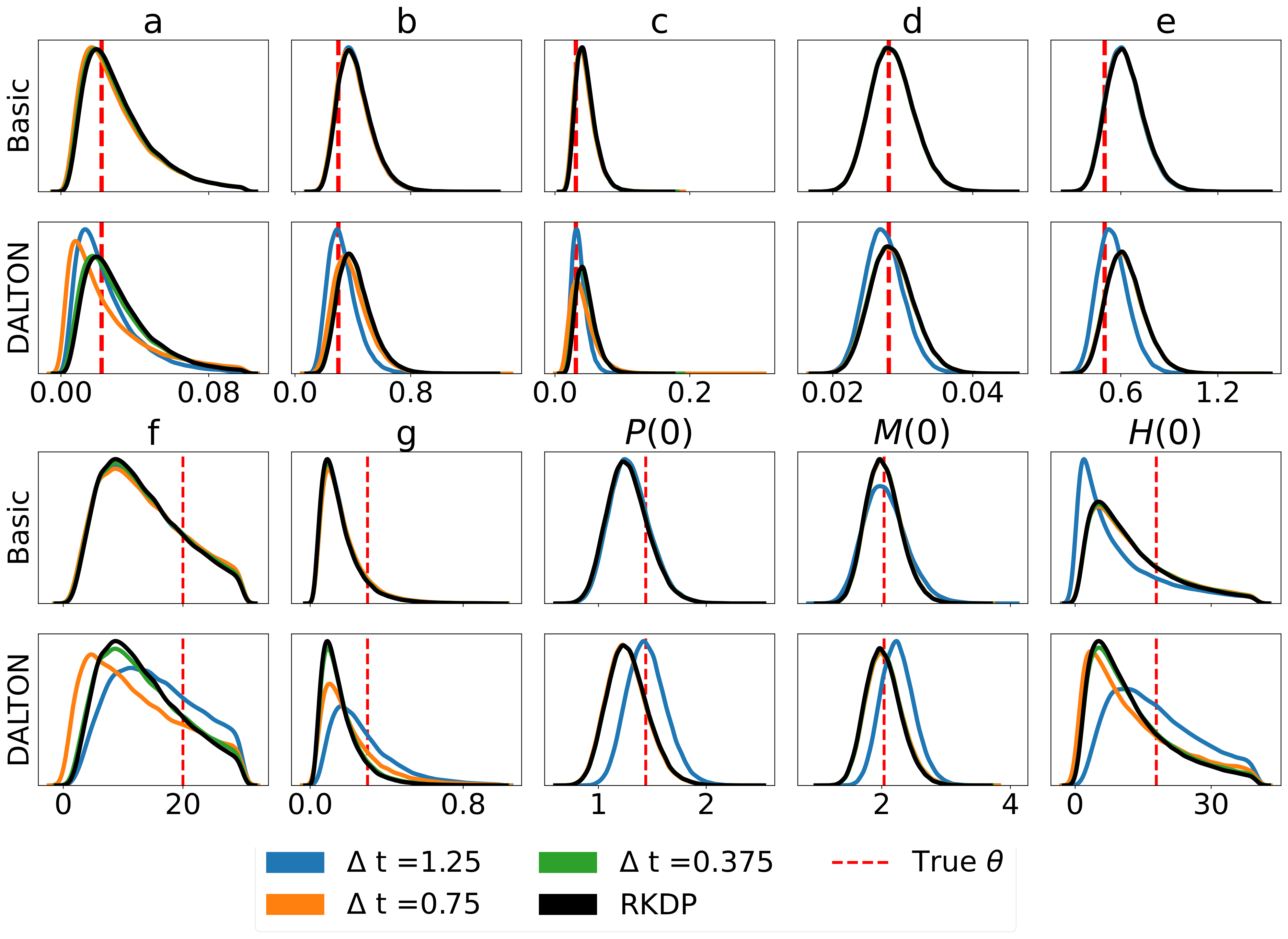
The unit tests can be ran through the following commands:
cd tests
python -m unittest discover -vOr, install tox, then from within rodeo enter command line: tox.
The HTML documentation can be compiled from the root folder:
pip install .[docs]
cd docs
make htmlThis will create the documentation in docs/build.