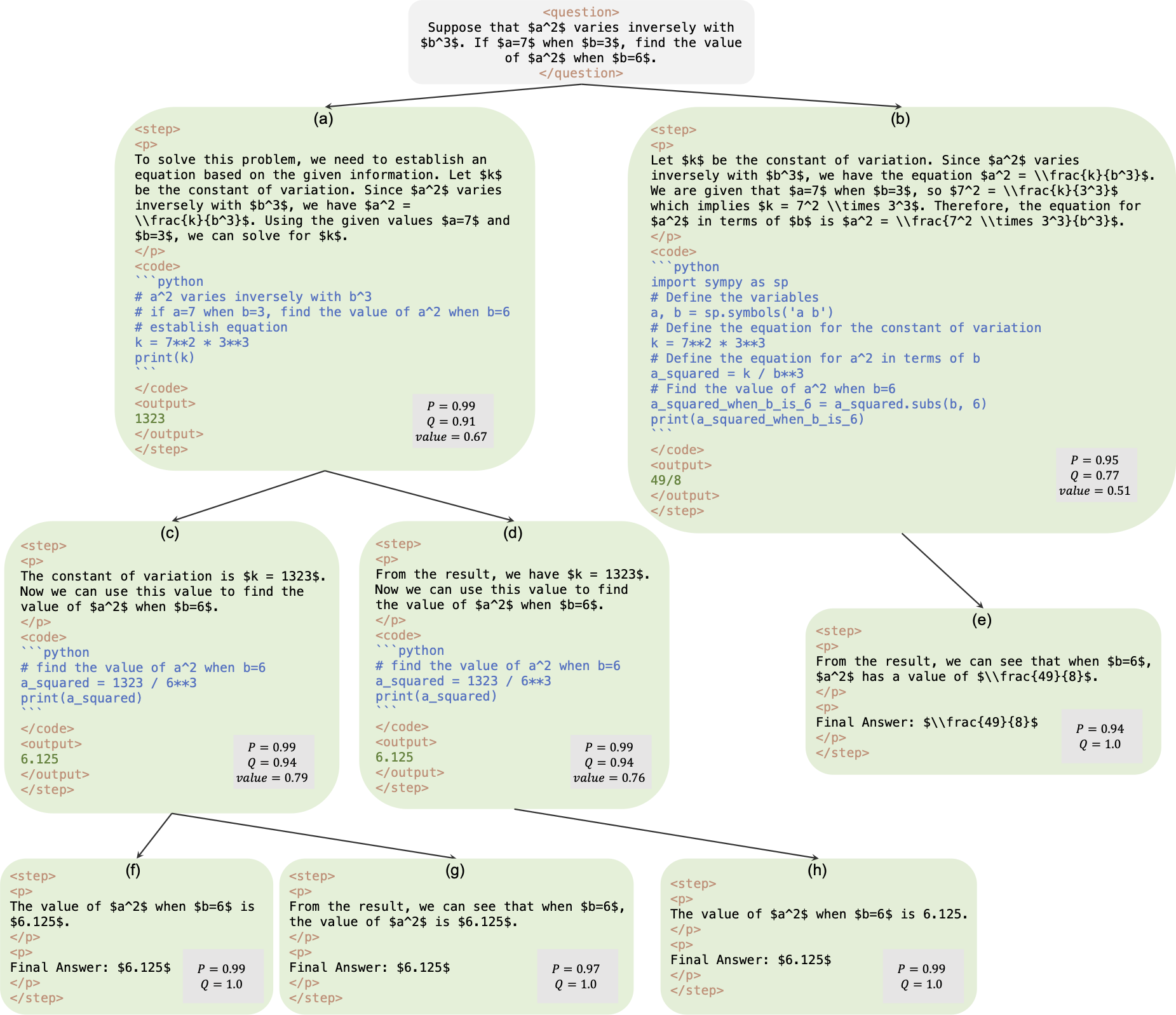
Este es el repositorio oficial de papel AlphaMath Almost Zero: supervisión de procesos sin proceso. El código se extrae de nuestra base de código corporativa interna. Como resultado, puede haber ligeras diferencias al reproducir las cifras reportadas en nuestro artículo, pero deberían ser muy cercanas. Nuestro enfoque implica entrenar los modelos de políticas y valores utilizando únicamente el razonamiento matemático derivado del marco de Monte Carlo Tree Search (MCTS), eliminando la necesidad de GPT-4 o anotaciones humanas. Esta es una ilustración de la instancia de capacitación generada por MCTS en la ronda 3.
Punto de control : ¿AlphaMath-7B ronda 3? / AlphaMath-7B ronda 3 ?
Conjunto de datos : AlphaMath-Round3-Trainset? El proceso de solución de los datos de capacitación se genera automáticamente en función de MCTS y el punto de control en la ronda 2. Se incluyen ejemplos tanto positivos como negativos para entrenar los modelos de políticas y valores.
Código de capacitación : debido a la política, solo podemos publicar los detalles de implementación de algunas funciones clave, que básicamente deben modificarse en su propio código de capacitación.
| Método de inferencia | Exactitud | promedio tiempo (s) por q | promedio pasos | # soles |
|---|---|---|---|---|
| Avaro | 53,62 | 1.6 | 3.1 | 1 |
| Maj@5 | 61,84 | 2.9 | 2.9 | 5 |
| Viga escalonada (1,5) | 62,32 | 3.1 | 3.0 | top-1 |
| 5 carreras + Maj@5 | 67.04 | x5 | x1 | 5 primeros 1 |
| Viga escalonada (2,5) | 64,66 | 2.4 | 2.4 | top-1 |
| Viga escalonada (3,5) | 65,74 | 2.3 | 2.2 | top-1 |
| Viga escalonada (5,5) | 65,98 | 4.7 | 2.3 | top-1 |
| 1 carrera + Maj@5 | 66,54 | x1 | x1 | top-5 |
| 5 carreras + Maj@5 | 69,94 | x5 | x1 | 5 primeros 1 |
| MCTS (N=40) | 64.02 | 10.1 | 3.8 | top-1 |
+ Maj@5 requiere ejecutarse 5 veces, lo que fomenta la diversidad.+ Maj@5 utiliza directamente a los 5 candidatos, que carecen de diversidad.| temperatura | 0,6 | 1.0 |
|---|---|---|
| Viga escalonada (1,5) | 62,32 | 62,76 |
| Viga escalonada (2,5) | 64,66 | 65,60 |
| Viga escalonada (3,5) | 65,74 | 66,28 |
| Viga escalonada (5,5) | 65,98 | 66,38 |
Para la búsqueda de haz a nivel de paso, configurar temperature=1.0 puede lograr resultados ligeramente mejores.
requirements.txt pip install -r requirements.txt
O simplemente sigue los cmds
> git clone https://github.com/MARIO-Math-Reasoning/Super_MARIO.git
> git clone https://github.com/MARIO-Math-Reasoning/MARIO_EVAL.git
> git clone https://github.com/MARIO-Math-Reasoning/vllm.git
> cd Super_MARIO && pip install -r requirements.txt && cd ..
> cd MARIO_EVAL/latex2sympy && pip install . && cd ..
> pip install -e .
> cd ../vllm
> pip install -e . scripts/save_value_head.py para agregar el valor head al LLM. Puede ejecutar cualquiera de los siguientes dos cmds. Puede haber una ligera diferencia de precisión entre los dos. En nuestra máquina, el primero obtuvo el 53,4% y el segundo el 53,62%.
python react_batch_demo.py
--custom_cfg configs/react_sft.yaml
--qaf ../MARIO_EVAL/data/math_testset_annotation.json
o
# use step_beam (1, 1) without value func
python solver_demo.py
--custom_cfg configs/sbs_greedy.yaml
--qaf ../MARIO_EVAL/data/math_testset_annotation.json
En nuestra máquina, en el conjunto de pruebas MATH, el siguiente cmd con configuración B1=1, B2=5 puede alcanzar ~62%, y el que tiene configuración B1=3, B2=5 puede alcanzar ~65%.
python solver_demo.py
--custom_cfg configs/sbs_sft.yaml
--qaf ../MARIO_EVAL/data/math_testset_annotation.json
Calcular la precisión
python eval_output_jsonl.py
--res_file <the saved tree jsonl file by solver_demo.py>
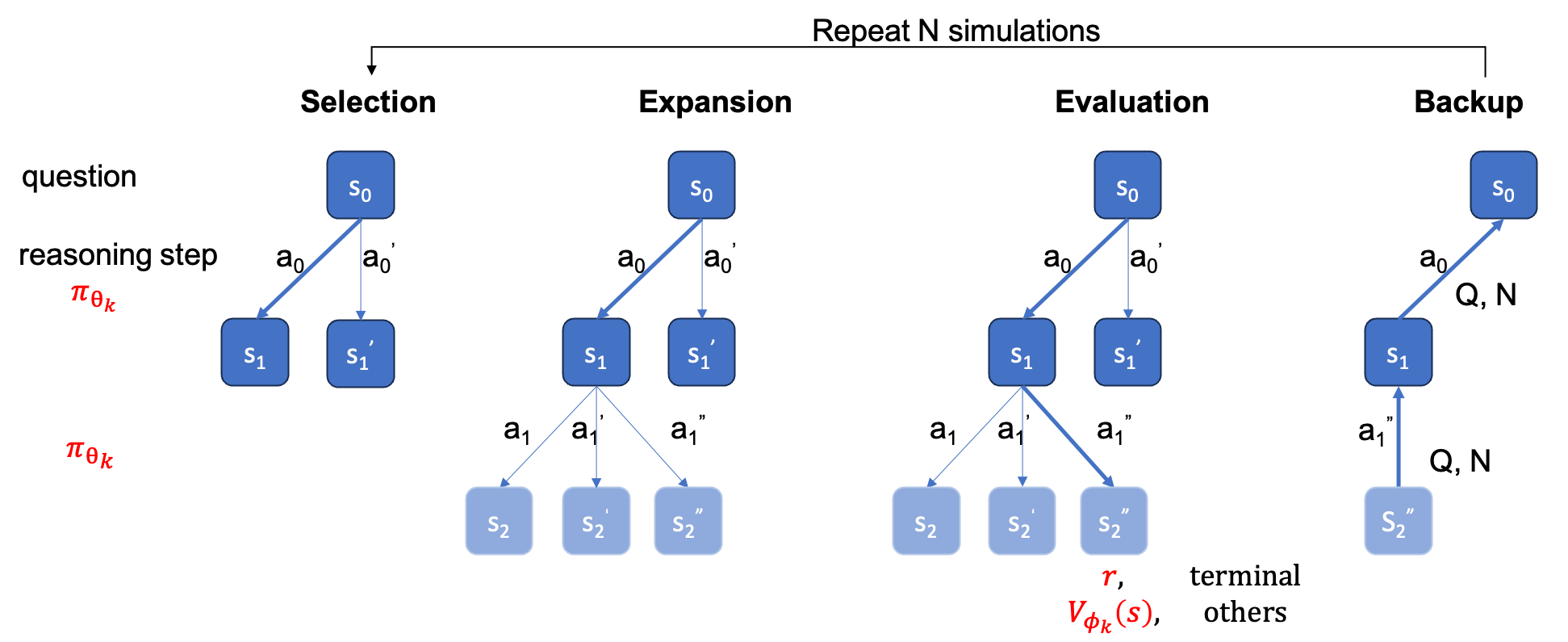
ground_truth (la respuesta final, no el proceso de solución) debe proporcionarse en un archivo qaf json o jsonl (un formato de ejemplo puede referirse a ../MARIO_EVAL/data/math_testset_annotation.json ).
ronda 1
# Checkpoint Initialization is required by adding value head
python solver_demo.py
--custom_cfg configs/mcts_round1.yaml
--qaf /path/to/training/data
ronda > 1, después de SFT
python solver_demo.py
--custom_cfg configs/mcts_sft_round.yaml
--qaf /path/to/training/data
Solo se utilizará question para generar la solución, pero ground_truth se utilizará para calcular la precisión.
python solver_demo.py
--custom_cfg configs/mcts_sft.yaml
--qaf ../MARIO_EVAL/data/math_testset_annotation.json
A diferencia de la búsqueda de haces a nivel de paso, primero debe crear un árbol completo, luego debe ejecutar el MCTS sin conexión y luego calcular la precisión.
python offline_inference.py
--custom_cfg configs/offline_inference.yaml
--tree_jsonl <the saved tree jsonl file by solver_demo.py>
Nota: este script de evaluación también se puede ejecutar con el árbol guardado mediante la búsqueda de vigas a nivel de paso, y la precisión debe seguir siendo la misma.
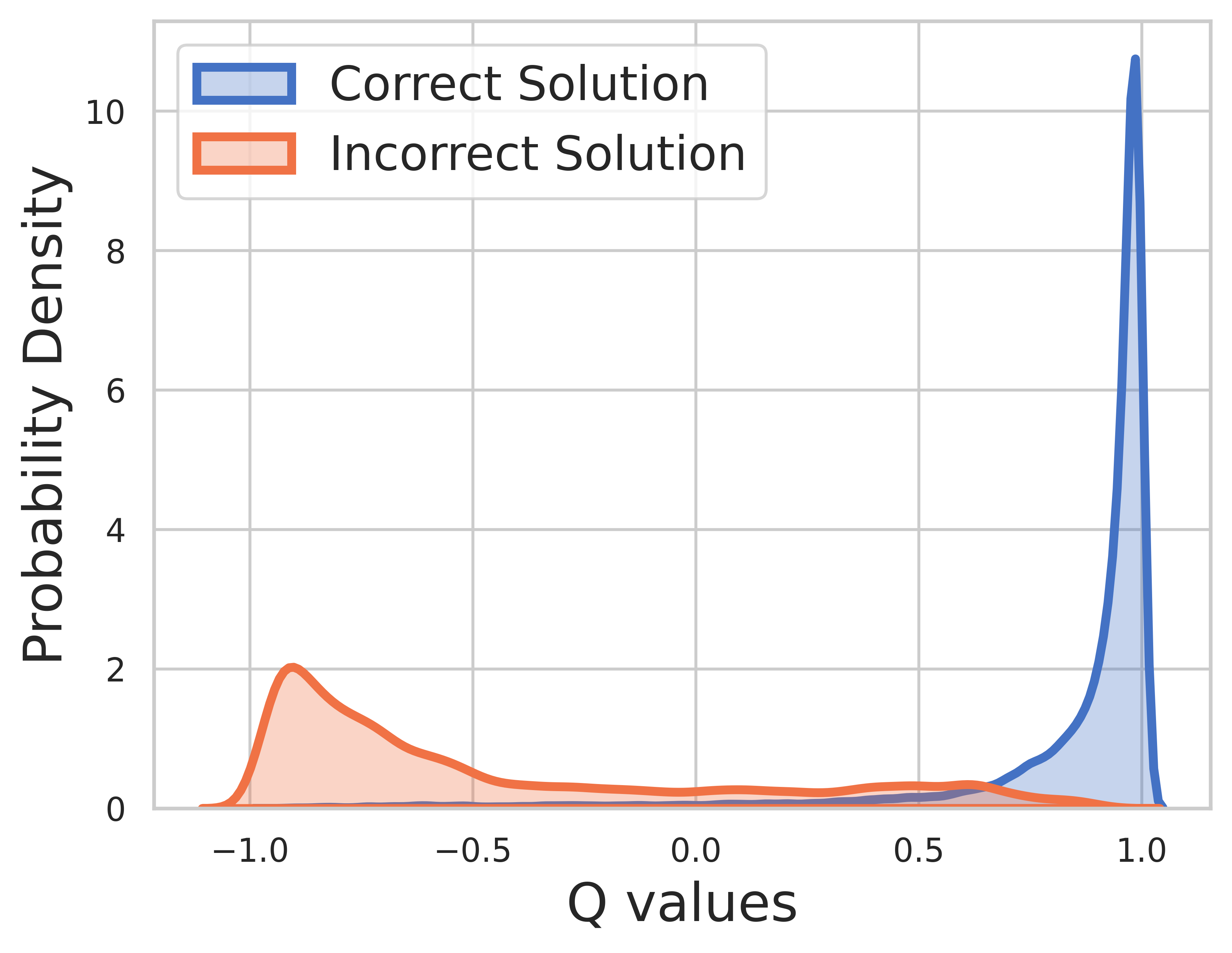
Debido a que la verdad fundamental es conocida para los datos de entrenamiento, el valor del paso final es la recompensa y el valor Q puede converger muy bien.
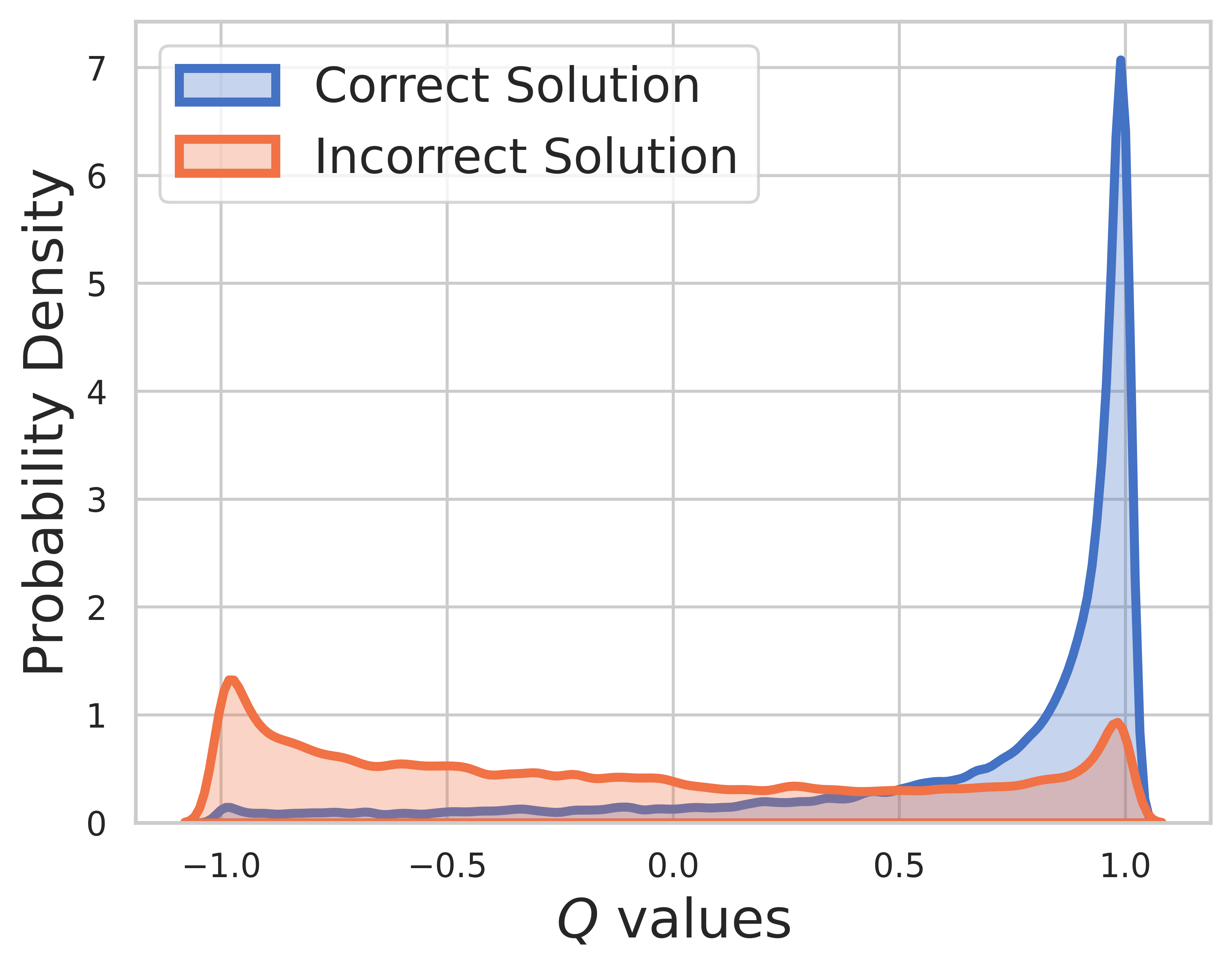
En el conjunto de prueba, se desconoce la verdad fundamental, por lo que la distribución del valor Q incluye pasos intermedios y finales. De esta figura podemos encontrar
SVPO por MCTS
@misc{chen2024steplevelvaluepreferenceoptimization,
title={Step-level Value Preference Optimization for Mathematical Reasoning},
author={Guoxin Chen and Minpeng Liao and Chengxi Li and Kai Fan},
year={2024},
eprint={2406.10858},
archivePrefix={arXiv},
primaryClass={cs.CL},
url={https://arxiv.org/abs/2406.10858},
}
Versión MCTS
@misc{chen2024alphamathzeroprocesssupervision,
title={AlphaMath Almost Zero: process Supervision without process},
author={Guoxin Chen and Minpeng Liao and Chengxi Li and Kai Fan},
year={2024},
eprint={2405.03553},
archivePrefix={arXiv},
primaryClass={cs.CL},
url={https://arxiv.org/abs/2405.03553},
}
Kit de herramientas de evaluación
@misc{zhang2024marioevalevaluatemath,
title={MARIO Eval: Evaluate Your Math LLM with your Math LLM--A mathematical dataset evaluation toolkit},
author={Boning Zhang and Chengxi Li and Kai Fan},
year={2024},
eprint={2404.13925},
archivePrefix={arXiv},
primaryClass={cs.CL},
url={https://arxiv.org/abs/2404.13925},
}
Versión OVM (modelo de valor de resultados)
@misc{liao2024mariomathreasoningcode,
title={MARIO: MAth Reasoning with code Interpreter Output -- A Reproducible Pipeline},
author={Minpeng Liao and Wei Luo and Chengxi Li and Jing Wu and Kai Fan},
year={2024},
eprint={2401.08190},
archivePrefix={arXiv},
primaryClass={cs.CL},
url={https://arxiv.org/abs/2401.08190},
}