El remuestreo de Lanczos (pronunciado Lanchos) es una técnica sofisticada para interpolar señales digitales, que ofrece una calidad de imagen superior en comparación con métodos más simples como el vecino más cercano y la interpolación bilineal. Al preservar eficazmente los detalles y minimizar los artefactos de aliasing, el remuestreo de Lanczos se utiliza ampliamente en aplicaciones de procesamiento de imágenes y señales.
Si bien Lanczos sobresale en calidad de imagen, esto tiene el costo de una mayor complejidad computacional. Además, la posibilidad de que se produzcan artefactos que "suenen", especialmente alrededor de bordes afilados, puede ser un inconveniente. A pesar de estos desafíos, Lanczos sigue siendo la opción preferida para tareas como el escalado y la rotación de imágenes debido a sus beneficios de rendimiento general.
Este documento proporciona una descripción general completa del remuestreo de Lanczos, incluidos sus fundamentos teóricos, detalles de implementación y aplicaciones prácticas. Sirve como un recurso valioso para desarrolladores e investigadores que buscan comprender y utilizar esta poderosa técnica. Las secciones siguientes profundizan en aspectos cruciales del remuestreo de Lanczos, como el núcleo de Lanczos, los procesos de interpolación y remuestreo, la preservación del flujo, el muestreo ascendente, descendente, el posicionamiento de la muestra, el rango de salida, la interpolación multidimensional y la separabilidad. Se incluye un ejemplo práctico con el código fuente adjunto.
El kernel de Lanczos, definido para un tamaño de soporte determinado, es una función utilizada en el remuestreo de Lanczos. El núcleo se define como:
L(x) = sinc(x)*sinc(x/a) : -a < x < a
= 0.0 : otherwise
Dónde:
La función sinc normalizada se define como:
sinc(x) = 1.0 : x = 0.0
= sin(PI*x)/(PI*x) : otherwise
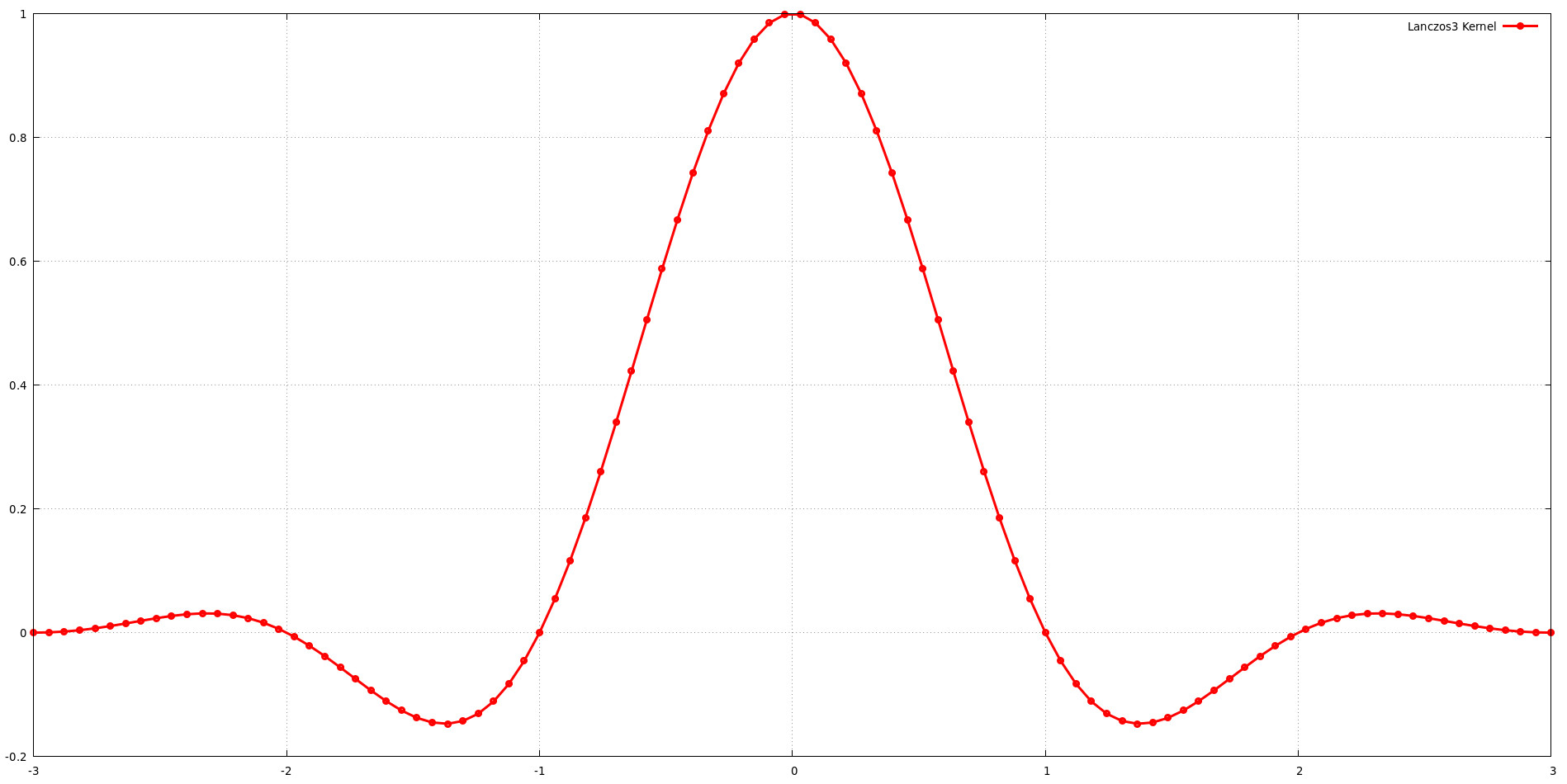
El gráfico ilustra la forma del núcleo de Lanczos para un tamaño de soporte de a = 3. Esto significa que el núcleo incluye tres lóbulos de la función sinc. Si bien aumentar el tamaño del soporte (a) generalmente proporciona más flexibilidad para dar forma a la respuesta de frecuencia, también aumenta el costo computacional. Se debe lograr un equilibrio entre la calidad de la imagen y la eficiencia computacional al elegir el tamaño del soporte. El hallazgo de Jim Blinn de que el núcleo de Lanczos con a = 3 ofrece un excelente equilibrio entre preservación de bajas frecuencias y rechazo de altas frecuencias respalda esta idea.
Nota: Los términos "ancho del grano", "tamaño del soporte" y "tamaño del filtro" a menudo se usan indistintamente para describir el parámetro a. Sin embargo, en el contexto del remuestreo de Lanczos, el "tamaño del soporte" refleja con mayor precisión el concepto.
La interpolación de Lanczos es una técnica utilizada para remuestrear una señal discreta a una nueva frecuencia de muestreo. Lo logra convolucionando la señal original con un núcleo Lanczos.
La señal interpolada s2(x) se puede calcular de la siguiente manera:
s2(x) = (1/w(x))*
SUM(i = -a + 1, i = a,
s1(floor(x) + i)*
L(i - x + floor(x)))
Dónde:
Preservar el flujo:
El factor de normalización w(x) es crucial para preservar la energía o masa general de la señal durante el proceso de interpolación. Garantiza que la suma de los valores interpolados se aproxima a la suma de las muestras originales. El peso del filtro se calcula como:
w(x) = SUM(i = -a + 1, i = a, L(i - x + floor(x)))
Muestreo ascendente:
Al aumentar la frecuencia de muestreo, la ecuación de interpolación de Lanczos se puede utilizar directamente sin modificaciones.
Reducción de resolución:
Para evitar artefactos de alias al disminuir la frecuencia de muestreo, la escala del filtro debe ajustarse para que coincida con la nueva frecuencia de muestreo.
fs = n1/n2
s2(x) = (1/w(x))*
SUM(i = -(fs*a) + 1, i = (fs*a),
s1(floor(x) + i)*
L((i - x + floor(x))/fs))
Dónde:
Al volver a muestrear una señal de n1 muestras a n2 muestras, se utilizan las siguientes posiciones de muestra. El índice j se utiliza para representar las muestras de la señal muestreada s2(x). El término (j + 0,5) es el centro de una muestra en s2(x). El paso escala un punto en s2(x) a un punto en s1(x). El término final -0,5 en x es un cambio de fase que hace que las muestras del coeficiente de Lanczos se compensen.
step = n1/n2
j = [0..n2)
x = (j + 0.5)*step - 0.5
Al realizar la interpolación de Lanczos, se debe tener especial cuidado en los límites de la señal. Las técnicas comunes de manejo de bordes incluyen:
Relleno cero:
s1(x) = s1[floor(x)] : x = [0, n1)
= 0.0 : otherwise
Reprimición:
s1(x) = s1[clamp(floor(x), 0, n1 - 1)]
A menudo se prefiere la sujeción, ya que reduce los artefactos en los bordes causados por discontinuidades agudas cerca de los bordes. Sin embargo, la elección del método de manipulación de bordes depende de la aplicación específica y del resultado deseado.
El rango de s2(x) puede ser mayor que el de s1(x) debido a los lóbulos de L(x). Por ejemplo, una señal de entrada s1(x) correspondiente a colores de píxeles en el rango de [0.0,1.0] debe fijarse en el mismo rango para garantizar que los valores de salida no se desborden cuando se vuelvan a convertir a bytes sin signo de [0,255]. .
El kernel de Lanczos se puede extender a múltiples dimensiones para realizar interpolación en imágenes o datos de dimensiones superiores.
El núcleo bidimensional de Lanczos se define como:
L(x, y) = sinc(sqrt(x^2 + y^2))*sinc(sqrt(x^2 + y^2)/a)
La señal interpolada s2(x, y) se puede calcular mediante la siguiente fórmula:
s2(x, y) = (1/w(x, y))*
SUM(i = -a + 1, i = a,
SUM(j = -a + 1, j = a,
s1(floor(x) + j, floor(y) + i)*
L(j - x + floor(x), i - y + floor(y))))
Donde w(x, y) es el factor de normalización calculado utilizando el núcleo bidimensional de Lanczos.
A diferencia de algunos métodos de interpolación, el núcleo de Lanczos no es separable, lo que significa que no se puede factorizar en el producto de núcleos unidimensionales. Esta propiedad generalmente genera costos computacionales más altos en comparación con los núcleos separables. Para mejorar el rendimiento, algunas implementaciones se aproximan al kernel de Lanczos realizando pases separados para las dimensiones horizontal y vertical.
Interpolación horizontal:
Interpolación vertical:
Representación matemática:
s2(x, y) = (1/w(x))*
SUM(j = -a + 1, j = a,
s1(floor(x) + j, y)*
L(j - x + floor(x)))
s3(x, y) = (1/w(y))*
SUM(i = -a + 1, i = a,
s2(x, floor(y) + i)*
L(i - y + floor(y)))
Tenga en cuenta que los factores de normalización w(x) y w(y) se calculan utilizando el núcleo unidimensional de Lanczos.
Puntos clave:
De manera similar, remuestreo recursivo de una señal varias veces, como se hace comúnmente para generar mapas MIP de textura, también puede degradar la calidad de la imagen debido a la acumulación de errores en cada paso de remuestreo.
Ejecute el ejemplo de prueba de lancos y use gnuplot para ver cómo el remuestreo de Lanczos afecta una señal unidimensional simple cuando se aumenta y disminuye el muestreo en un factor de 2.
make
./lanczos-test
gnuplot
> load "output.plot"
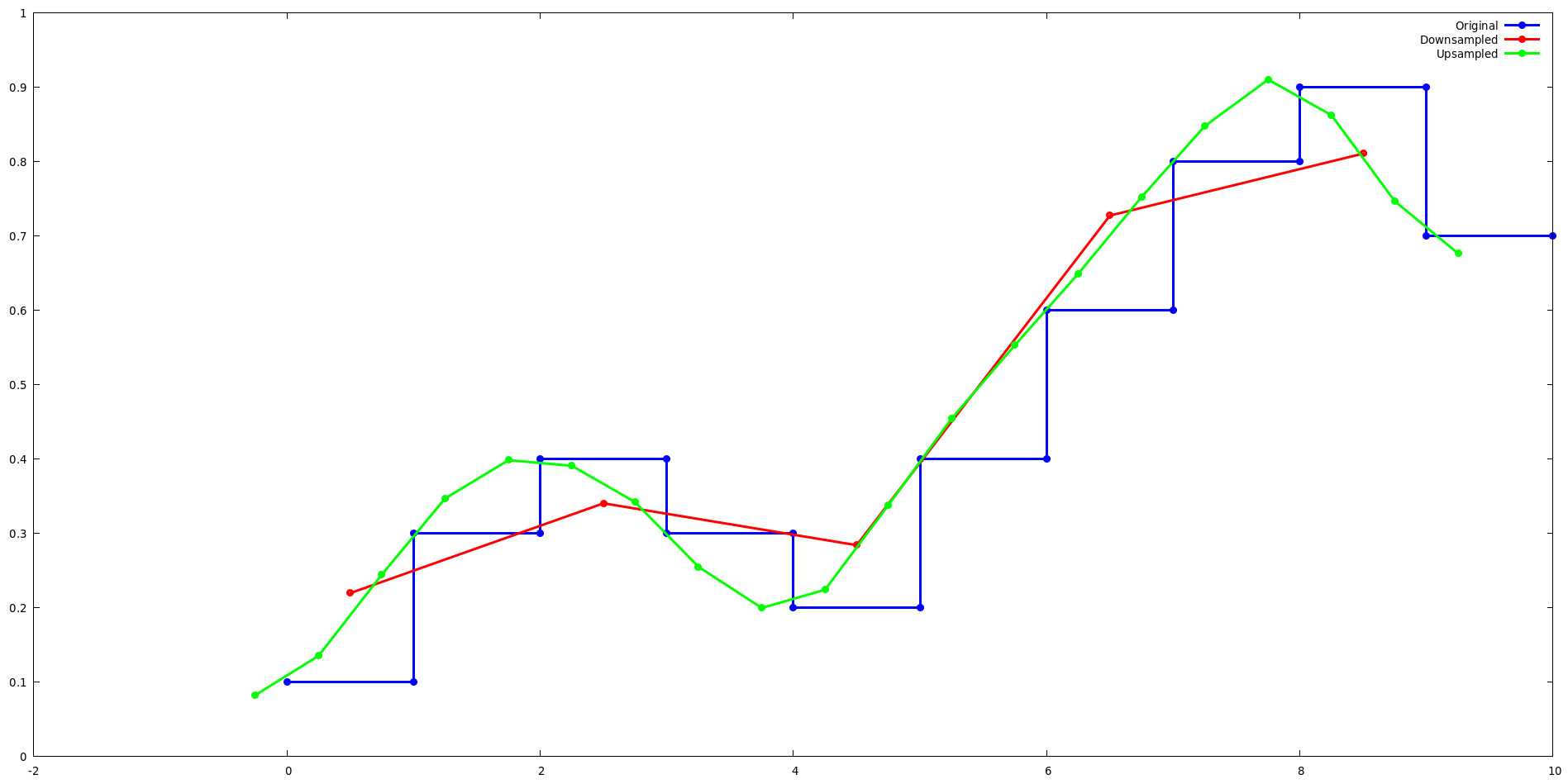
Muestreo ascendente:
Al realizar un muestreo superior mediante una potencia de dos, el núcleo de Lanczos alterna entre conjuntos de valores de 2^niveles. Por ejemplo, considere las primeras 4 salidas del ejemplo de muestra superior de lanzcos-test. Observe que las salidas para L(x) se repiten para j={0,2} y j={1,3}.
upsample n1=10, n2=20
j=0, x=-0.250000
i=-2, L(-2.750000)=0.007356, S1(-3.000000)=0.100000
i=-1, L(-1.750000)=-0.067791, S1(-2.000000)=0.100000
i=0, L(-0.750000)=0.270190, S1(-1.000000)=0.100000
i=1, L(0.250000)=0.890067, S1(0.000000)=0.100000
i=2, L(1.250000)=-0.132871, S1(1.000000)=0.300000
i=3, L(2.250000)=0.030021, S1(2.000000)=0.400000
s2=0.082129, s2/w=0.082379, w=0.996972
j=1, x=0.250000
i=-2, L(-2.250000)=0.030021, S1(-2.000000)=0.100000
i=-1, L(-1.250000)=-0.132871, S1(-1.000000)=0.100000
i=0, L(-0.250000)=0.890067, S1(0.000000)=0.100000
i=1, L(0.750000)=0.270190, S1(1.000000)=0.300000
i=2, L(1.750000)=-0.067791, S1(2.000000)=0.400000
i=3, L(2.750000)=0.007356, S1(3.000000)=0.300000
s2=0.134869, s2/w=0.135279, w=0.996972
j=2, x=0.750000
i=-2, L(-2.750000)=0.007356, S1(-2.000000)=0.100000
i=-1, L(-1.750000)=-0.067791, S1(-1.000000)=0.100000
i=0, L(-0.750000)=0.270190, S1(0.000000)=0.100000
i=1, L(0.250000)=0.890067, S1(1.000000)=0.300000
i=2, L(1.250000)=-0.132871, S1(2.000000)=0.400000
i=3, L(2.250000)=0.030021, S1(3.000000)=0.300000
s2=0.243853, s2/w=0.244594, w=0.996972
j=3, x=1.250000
i=-2, L(-2.250000)=0.030021, S1(-1.000000)=0.100000
i=-1, L(-1.250000)=-0.132871, S1(0.000000)=0.100000
i=0, L(-0.250000)=0.890067, S1(1.000000)=0.300000
i=1, L(0.750000)=0.270190, S1(2.000000)=0.400000
i=2, L(1.750000)=-0.067791, S1(3.000000)=0.300000
i=3, L(2.750000)=0.007356, S1(4.000000)=0.200000
s2=0.345945, s2/w=0.346996, w=0.996972
Reducción de resolución:
Cuando se reduce la resolución mediante una potencia de dos, el núcleo de Lanczos se vuelve independiente de x ya que (x - piso(x)) se convierte en una constante que coincide con el cambio de fase. Por ejemplo, considere las primeras 2 salidas del ejemplo de reducción de resolución de lanzcos-test. Observe que las salidas de L(x) se repiten para cada j.
downsample n1=10, n2=5
j=0, x=0.500000
i=-5, L(-2.750000)=0.007356, S1(-5.000000)=0.100000
i=-4, L(-2.250000)=0.030021, S1(-4.000000)=0.100000
i=-3, L(-1.750000)=-0.067791, S1(-3.000000)=0.100000
i=-2, L(-1.250000)=-0.132871, S1(-2.000000)=0.100000
i=-1, L(-0.750000)=0.270190, S1(-1.000000)=0.100000
i=0, L(-0.250000)=0.890067, S1(0.000000)=0.100000
i=1, L(0.250000)=0.890067, S1(1.000000)=0.300000
i=2, L(0.750000)=0.270190, S1(2.000000)=0.400000
i=3, L(1.250000)=-0.132871, S1(3.000000)=0.300000
i=4, L(1.750000)=-0.067791, S1(4.000000)=0.200000
i=5, L(2.250000)=0.030021, S1(5.000000)=0.400000
i=6, L(2.750000)=0.007356, S1(6.000000)=0.600000
s2=0.437796, s2/w=0.219563, w=1.993943
j=1, x=2.500000
i=-5, L(-2.750000)=0.007356, S1(-3.000000)=0.100000
i=-4, L(-2.250000)=0.030021, S1(-2.000000)=0.100000
i=-3, L(-1.750000)=-0.067791, S1(-1.000000)=0.100000
i=-2, L(-1.250000)=-0.132871, S1(0.000000)=0.100000
i=-1, L(-0.750000)=0.270190, S1(1.000000)=0.300000
i=0, L(-0.250000)=0.890067, S1(2.000000)=0.400000
i=1, L(0.250000)=0.890067, S1(3.000000)=0.300000
i=2, L(0.750000)=0.270190, S1(4.000000)=0.200000
i=3, L(1.250000)=-0.132871, S1(5.000000)=0.400000
i=4, L(1.750000)=-0.067791, S1(6.000000)=0.600000
i=5, L(2.250000)=0.030021, S1(7.000000)=0.800000
i=6, L(2.750000)=0.007356, S1(8.000000)=0.900000
s2=0.678627, s2/w=0.340344, w=1.993943
Como optimización adicional, el kernel de Lanczos puede precalcularse para estos casos para eliminar el costoso cálculo de la función sinc.
Este README fue creado con la ayuda de Google Gemini.
Las referencias adicionales incluyen:
Este código fue implementado por Jeff Boody bajo la licencia MIT.
Copyright (c) 2024 Jeff Boody
Permission is hereby granted, free of charge, to any person obtaining a
copy of this software and associated documentation files (the "Software"),
to deal in the Software without restriction, including without limitation
the rights to use, copy, modify, merge, publish, distribute, sublicense,
and/or sell copies of the Software, and to permit persons to whom the
Software is furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included
in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN
THE SOFTWARE.