Bosonic es una biblioteca desarrollada para la simulación de sistemas fotónicos cuyas entradas son bosones indistinguibles (en el caso de interés de los autores, fotones). En particular, se centra en el cálculo rápido de las funciones de transferencia de múltiples partículas para estos sistemas y respalda el cálculo del gradiente de una función de costo con respecto a los parámetros del sistema. Fue desarrollado originalmente para el desarrollo de nuestras Redes Neuronales Ópticas Cuánticas [1] y contiene funcionalidad especializada para su simulación y optimización.
Los enfoques clave de esta biblioteca fueron dos:
La motivación principal para este paquete fue el cálculo rápido de la transformada unitaria de múltiples partículas en función de la partícula unitaria y el número de entradas bosónicas. Es decir, si tenemos una U unitaria de cuatro dimensiones y sabemos que hay 3 fotones en la entrada, queremos saber la transformación sobre la
Esto está respaldado por la función bosonic.aa_phi , que lleva el nombre de Aaronson y Arkhipov, quienes especificaron la forma de esta función que usamos como su función Φ(U) en [2]. Por ejemplo, podemos demostrar el famoso efecto Hong-Ou-Mandel con un divisor de haz:
>> > import bosonic as b
>> > import numpy as np
>> > U = np . array ([[ 1 , 1 ], [ 1 , - 1 ]], dtype = complex ) / np . sqrt ( 2 )
>> > phiU = b . aa_phi ( U , 2 )
>> > print ( phiU )
[[ 0.5 + 0.j 0.70710678 + 0.j 0.5 + 0.j ]
[ 0.70710678 + 0.j 0. + 0.j - 0.70710678 + 0.j ]
[ 0.5 + 0.j - 0.70710678 + 0.j 0.5 + 0.j ]]
>> > print ( b . fock . basis ( 2 , 2 ))
[[ 2 , 0 ], [ 1 , 1 ], [ 0 , 2 ]]
>> > input = np . array ([[ 0 ], [ 1 ], [ 0 ]], dtype = complex )
>> > phiU = b . aa_phi ( U , 2 )
>> > print ( phiU . dot ( input ))
[[ 0.70710678 + 0.j ]
[ 0. + 0.j ]
[ - 0.70710678 + 0.j ]]
>> > print ( np . abs ( phiU . dot ( input )) ** 2 )
[[ 0.5 ]
[ 0. ]
[ 0.5 ]]Aquí, construimos el unitario correspondiente a un divisor de haz 50/50 en U. Como se muestra en la línea después de imprimir phiU, la base aquí es [2, 0], [1, 1] y [0, 2]. Entonces, el estado correspondiente a un fotón incidente en cada una de las entradas es [0, 1, 0]. En la última línea, dos líneas, vemos que la salida es una superposición igual de dos fotones en una salida y dos fotones en la otra, sin probabilidad de que los fotones salgan por puertos diferentes.
Como se describe en [1], hemos desarrollado una arquitectura propuesta para redes neuronales ópticas cuánticas que implica combinar transformaciones unitarias arbitrarias con no linealidades de sitio único. Consulte el documento para obtener más detalles, pero aquí hay un resumen visual de la arquitectura:
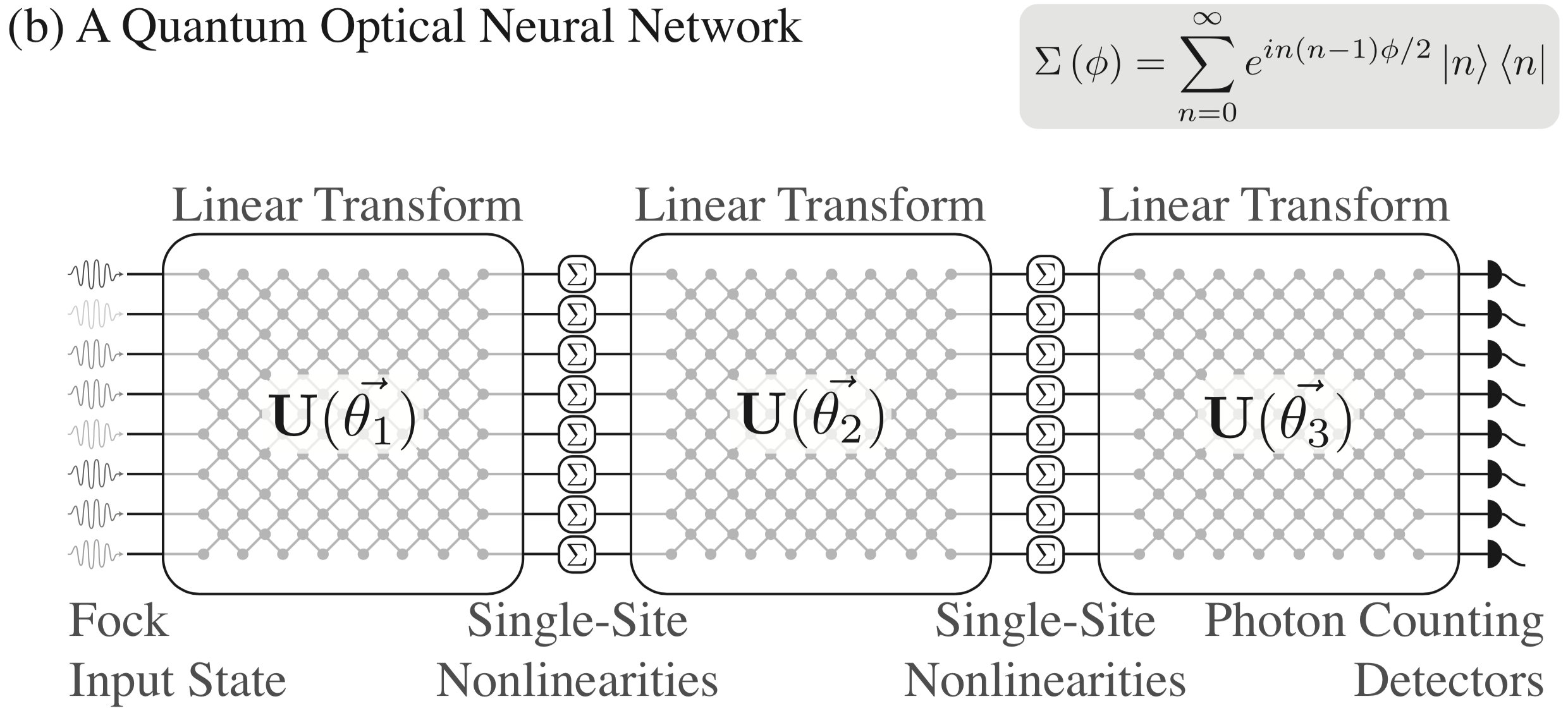
Clonar este repositorio es actualmente la única forma de obtener bosonic en su sistema. Antes de hacer eso, necesitará tener instalado el paquete de Python Cython para compilar bosonic correctamente. Algo como esto debería funcionar en Linux (usando su administrador de paquetes de Python preferido en lugar de pip , si lo desea):
$ pip install Cython
$ git clone [email protected]:steinbrecher/bosonic.git
$ cd bosonic
$ pip install .En Mac, también necesitarás gcc de homebrew y libopenmp:
$ brew install gcc
$ brew install libomp
$ pip install Cython
$ git clone [email protected]:steinbrecher/bosonic.git
$ cd bosonic
$ CC=gcc-8 pip install . Entonces deberías poder probar que bosonic está instalado correctamente ejecutando
$ python setup.py test[1] Steinbrecher, GR, Olson, JP, Englund, D. y Carolan, J. (2018). Redes neuronales ópticas cuánticas. arXiv preimpresión arXiv:1808.10047. https://arxiv.org/abs/1808.10047
[2] Aaronson, Scott y Alex Arkhipov. "La complejidad computacional de la óptica lineal". Actas del cuadragésimo tercer simposio anual de ACM sobre teoría de la informática. ACM, 2011. https://arxiv.org/pdf/1011.3245.pdf