

¡El paquete FRK está disponible en CRAN! Para instalar, por favor escriba
install.packages( " FRK " ) Para instalar la versión de desarrollo más reciente, cargue devtools y escriba
install_github( " andrewzm/FRK " , dependencies = TRUE , build_vignettes = TRUE )Un documento que presenta el paquete está disponible aquí. Un artículo que detalla el enfoque en un entorno no gaussiano está disponible aquí (un resumen de seis páginas de este artículo está disponible aquí).
La viñeta "FRK_intro" resume el paquete, brinda detalles sobre el algoritmo EM que puede emplearse en un entorno gaussiano y proporciona varios ejemplos. Otra viñeta, "FRK_non-Gaussian", resume la inferencia en un entorno no gaussiano (donde se utiliza una aproximación de Laplace) y contiene ejemplos que utilizan datos no gaussianos y los métodos de trazado recientemente disponibles. Para acceder a las viñetas, haga clic en los siguientes enlaces:
Introducción a FRK
Tutorial sobre modelado de datos no gaussianos espaciales y espacio-temporales con FRK
Una página pkgdown también está disponible aquí.
Si utiliza FRK en su trabajo, investigación u otras actividades, cítelo utilizando la información proporcionada por citation("FRK") .
Paquete: FRK
Tipo: Paquete
Título: Kriging de rango fijo
Versión: 2.3.1
Fecha: 2024-07-16
Autor: Andrew Zammit-Mangion, Matthew Sainsbury-Dale
Mantenedor: Andrew Zammit-Mangion [email protected]
Descripción: Una herramienta para modelado y predicción espacial/espacio-temporal con grandes conjuntos de datos. El enfoque modela el campo y, por tanto, la función de covarianza, utilizando un conjunto de funciones básicas. Esta representación de función base de rango fijo facilita el modelado de big data y el método, naturalmente, permite funciones de covarianza anisotrópicas no estacionarias. La discretización del dominio espacial en las denominadas unidades de área básicas (BAU, por sus siglas en inglés) facilita el uso de observaciones con soporte variable (es decir, soportes tanto de referencia puntual como de área, potencialmente simultáneamente) y la predicción sobre regiones arbitrarias especificadas por el usuario. FRK también admite la inferencia sobre varias variedades, incluidos el plano 2D y la esfera 3D, y proporciona funciones auxiliares para modelar, ajustar, predecir y trazar con relativa facilidad. La versión 2.0.0 y superiores también admiten el modelado de datos no gaussianos (por ejemplo, Poisson, binomiales, binomiales negativos, gamma y gaussianos inversos) mediante el empleo de un marco de modelo lineal mixto generalizado (GLMM). Zammit-Mangion y Cressie (2021) describen FRK en un entorno gaussiano y detallan su uso de funciones básicas y BAU, mientras que Sainsbury-Dale et al. (2024) describen FRK en un entorno no gaussiano; Hay dos viñetas disponibles que resumen estos artículos y brindan ejemplos adicionales.
Licencia: GPL (>= 2)
library( " FRK " )
library( " sp " )
library( " ggplot2 " )
library( " ggpubr " )
# # Setup
m <- 1000 # Sample size
RNGversion( " 3.6.0 " ); set.seed( 1 ) # Fix seed
zdf <- data.frame ( x = runif( m ), y = runif( m )) # Generate random locs
zdf $ z <- sin( 8 * zdf $ x ) + cos( 8 * zdf $ y ) + 0.5 * rnorm( m ) # Simulate data
coordinates( zdf ) = ~ x + y # Turn into sp object
# # Run FRK
S <- FRK( f = z ~ 1 , # Formula to FRK
list ( zdf ), # All datasets are supplied in list
n_EM = 10 ) # Max number of EM iterations
pred <- predict( S ) # Prediction stage
# # Plotting
plotlist <- plot( S , pred )
ggarrange( plotlist = plotlist , nrow = 1 , legend = " top " )
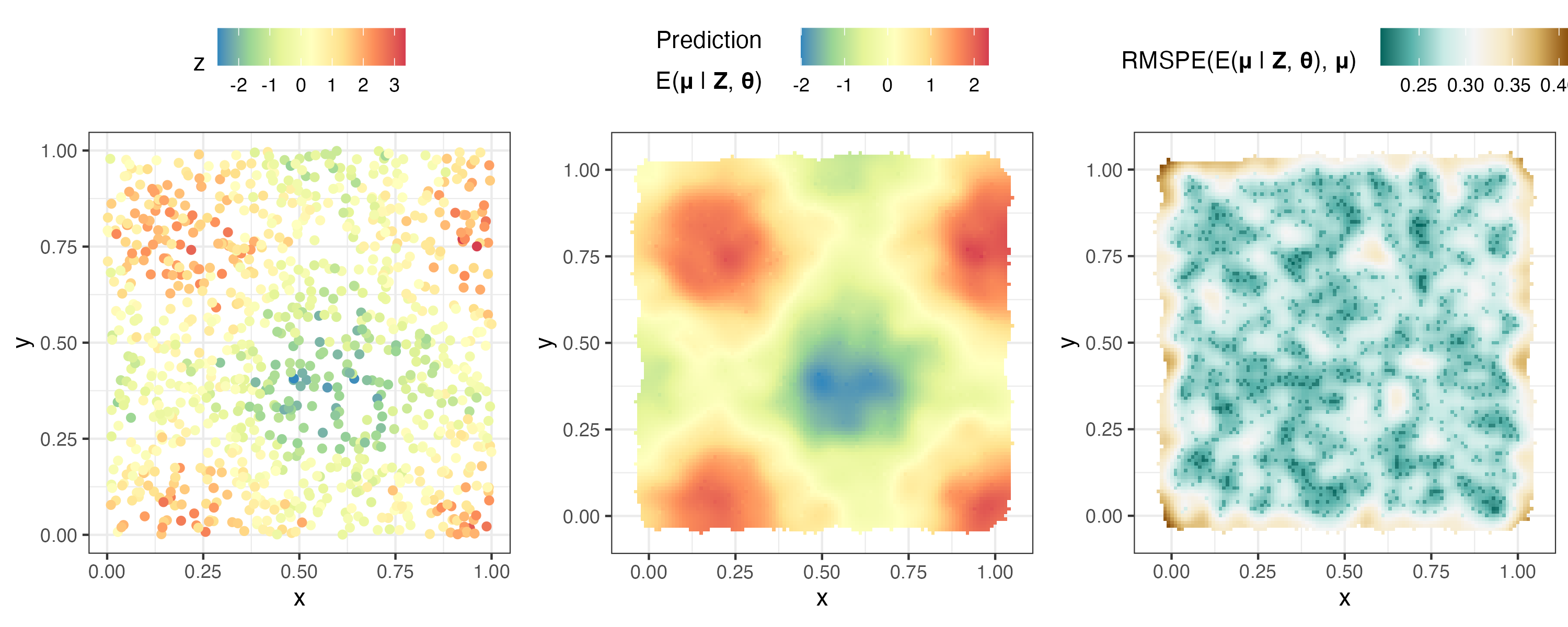
Aquí analizamos datos de Poisson simulados. Nos referimos a un modelo de datos de Poisson con una respuesta media que se modela utilizando la función de enlace de raíz cuadrada configurando response = "poisson" y link = "sqrt" en FRK() . Otras distribuciones de respuesta no gaussianas disponibles en FRK son las distribuciones binomial, binomial negativa, gamma y gaussiana inversa.
# # Simulate Poisson data using the previous example's data to construct a mean
zdf $ z <- rpois( m , lambda = zdf $ z ^ 2 )
# # Run FRK
S <- FRK( f = z ~ 1 , list ( zdf ),
response = " poisson " , # Poisson data model
link = " sqrt " ) # square-root link function
pred <- predict( S )
# # Plotting
plotlist <- plot( S , pred $ newdata )
ggarrange( plotlist $ z , plotlist $ p_mu , plotlist $ interval90_mu ,
nrow = 1 , legend = " top " )
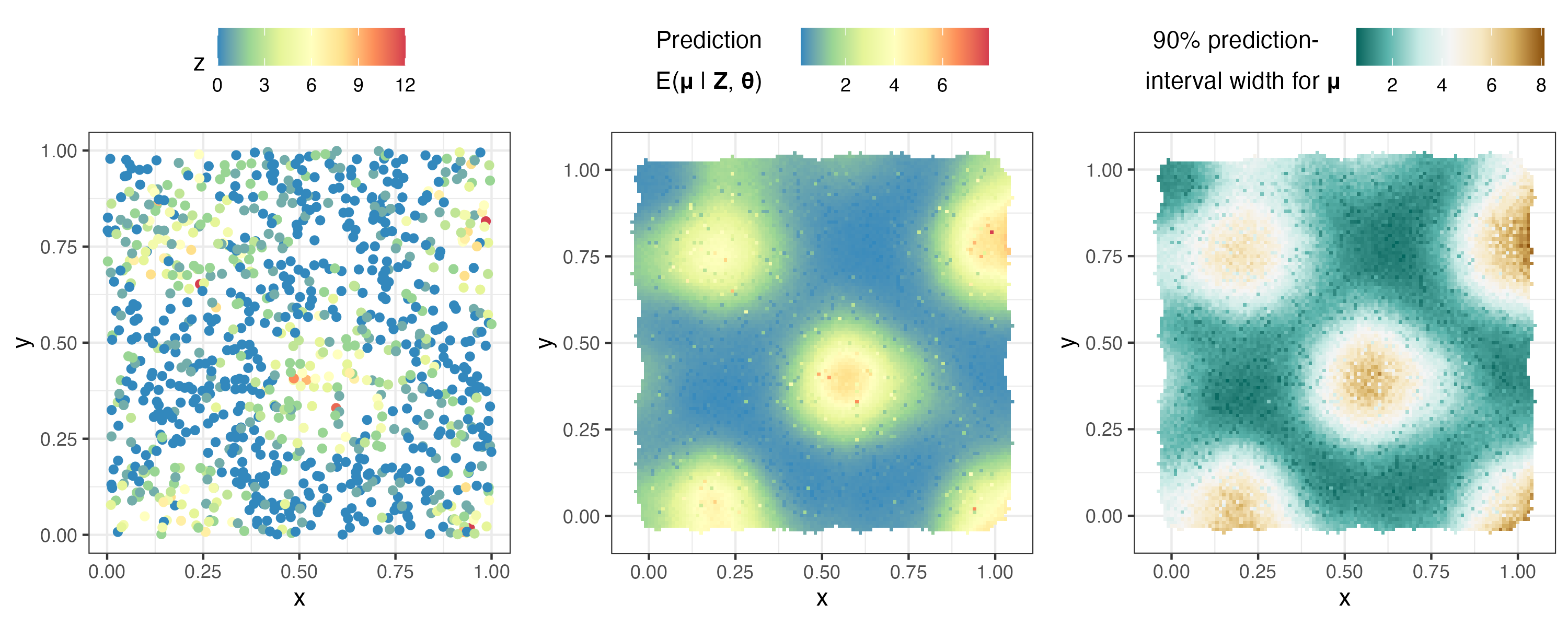
Ahora analizamos datos espacio-temporales utilizando el conjunto de datos de la NOAA.
# # Setup
library( " spacetime " )
data( " NOAA_df_1990 " )
Tmax <- subset( NOAA_df_1990 , month %in% 7 & year == 1993 )
Tmax <- within( Tmax , { time = as.Date(paste( year , month , day , sep = " - " ))})
STObj <- stConstruct( x = Tmax , space = c( " lon " , " lat " ), time = " time " , interval = TRUE )
# # BAUs: spatial BAUs are 1x1 pixels, temporal BAUs are 1 day intervals
BAUs <- auto_BAUs( manifold = STplane(),
cellsize = c( 1 , 1 , 1 ),
data = STObj , tunit = " days " )
BAUs $ fs <- 1 # scalar fine-scale variance matrix, implicit in previous examples
# # Basis functions
G <- auto_basis( manifold = STplane(), data = STObj , nres = 2 , tunit = " days " )
# # Run FRK
STObj $ std <- 2 # fix the measurement error variance
S <- FRK( f = z ~ 1 + lat , data = list ( STObj ),
basis = G , BAUs = BAUs , est_error = FALSE , method = " TMB " )
pred <- predict( S , percentiles = NULL )
# # Plotting: include only some times via the argument subset_time
plotlist <- plot( S , pred $ newdata , subset_time = c( 1 , 7 , 13 , 19 , 25 , 31 ))
ggarrange( plotlist = plotlist , nrow = 1 , legend = " top " )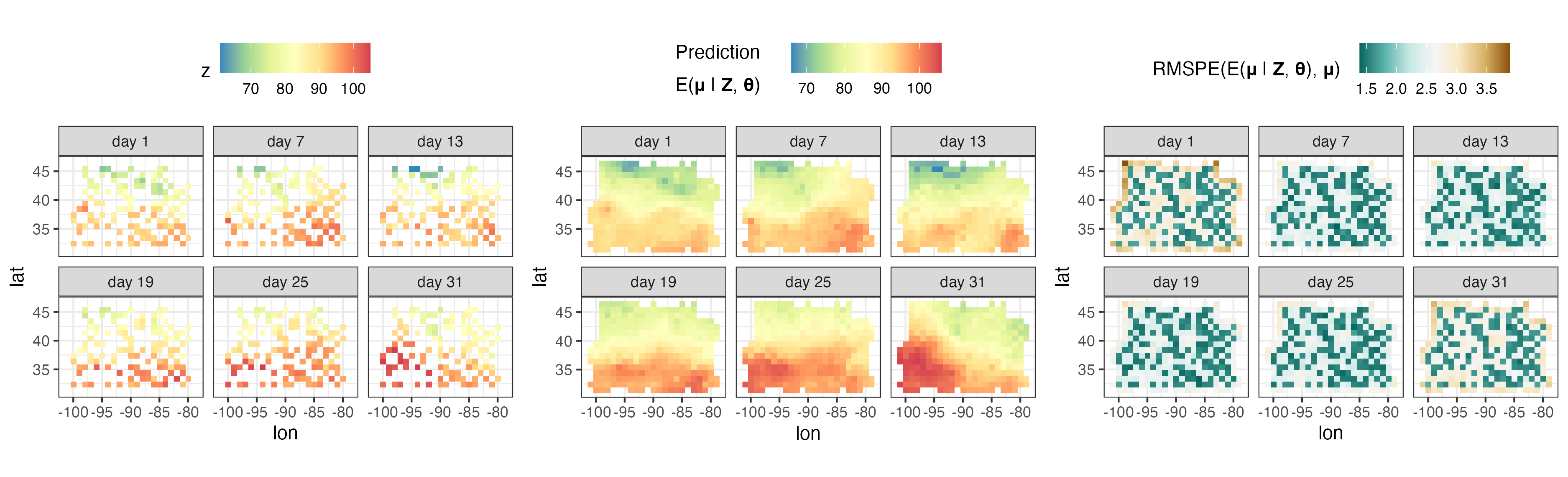
El paquete FRK se utiliza actualmente para generar animaciones espacio-temporales de campos observados mediante datos satelitales. Aquí mostramos una predicción diaria de CO2 utilizando datos del OCO-2 de la NASA entre septiembre de 2014 y junio de 2016.
¡Gracias a Michael Bertolacci por diseñar el logotipo hexagonal de FRK!