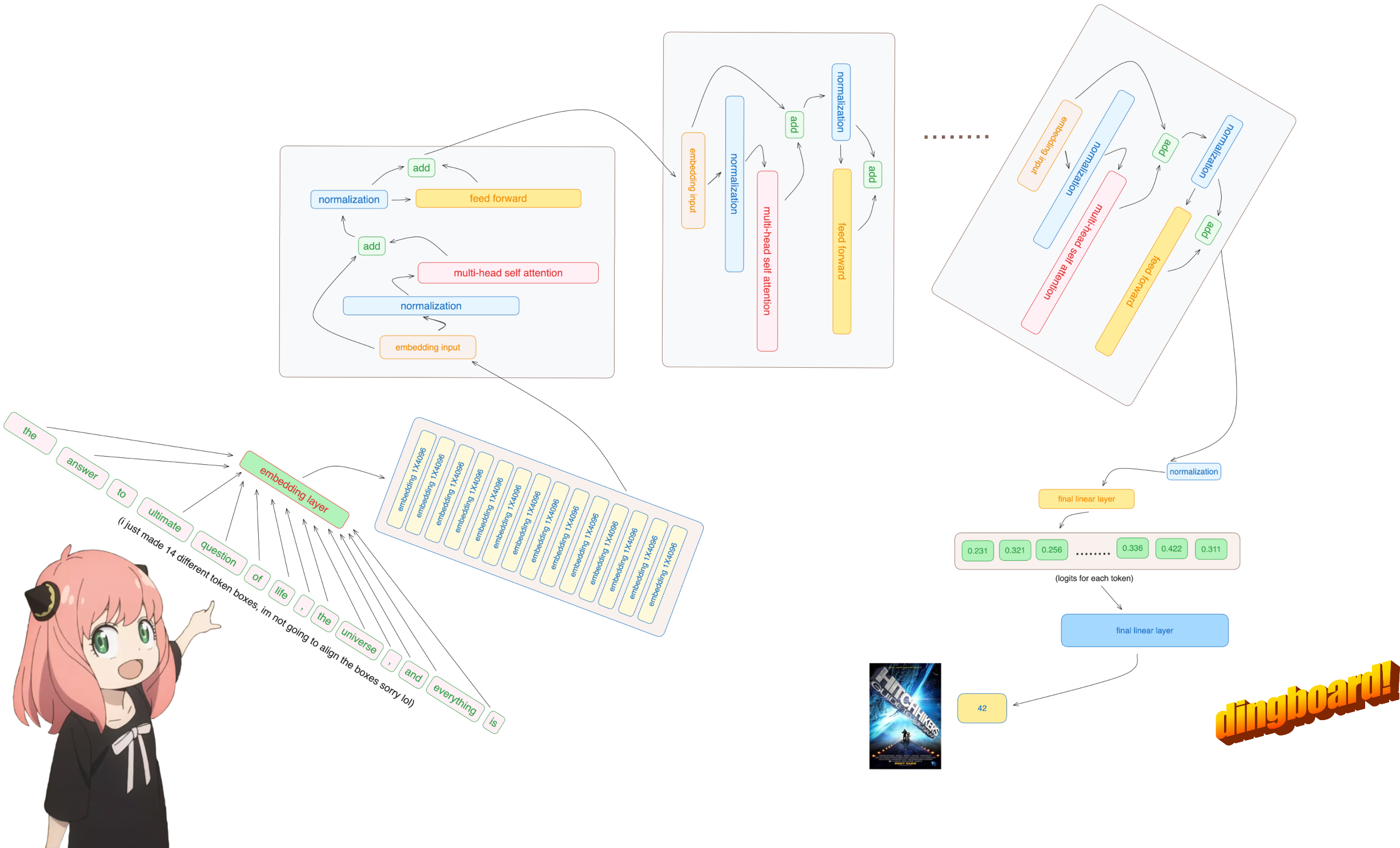
En este archivo, implementé llama3 desde cero, un tensor y una multiplicación de matrices a la vez.
Además, voy a cargar tensores directamente desde el archivo de modelo que meta proporcionó para llama3, debes descargar los pesos antes de ejecutar este archivo. aquí está el enlace oficial para descargar las pesas: https://llama.meta.com/llama-downloads/
No voy a implementar un tokenizador bpe (pero andrej karpathy tiene una implementación realmente limpia)
enlace a su implementación: https://github.com/karpathy/minbpe
from pathlib import Path
import tiktoken
from tiktoken . load import load_tiktoken_bpe
import torch
import json
import matplotlib . pyplot as plt
tokenizer_path = "Meta-Llama-3-8B/tokenizer.model"
special_tokens = [
"<|begin_of_text|>" ,
"<|end_of_text|>" ,
"<|reserved_special_token_0|>" ,
"<|reserved_special_token_1|>" ,
"<|reserved_special_token_2|>" ,
"<|reserved_special_token_3|>" ,
"<|start_header_id|>" ,
"<|end_header_id|>" ,
"<|reserved_special_token_4|>" ,
"<|eot_id|>" , # end of turn
] + [ f"<|reserved_special_token_ { i } |>" for i in range ( 5 , 256 - 5 )]
mergeable_ranks = load_tiktoken_bpe ( tokenizer_path )
tokenizer = tiktoken . Encoding (
name = Path ( tokenizer_path ). name ,
pat_str = r"(?i:'s|'t|'re|'ve|'m|'ll|'d)|[^rnp{L}p{N}]?p{L}+|p{N}{1,3}| ?[^sp{L}p{N}]+[rn]*|s*[rn]+|s+(?!S)|s+" ,
mergeable_ranks = mergeable_ranks ,
special_tokens = { token : len ( mergeable_ranks ) + i for i , token in enumerate ( special_tokens )},
)
tokenizer . decode ( tokenizer . encode ( "hello world!" )) 'hello world!'
Normalmente, leer esto depende de cómo están escritas las clases del modelo y los nombres de las variables dentro de ellas.
pero como estamos implementando llama3 desde cero, leeremos el archivo un tensor a la vez.
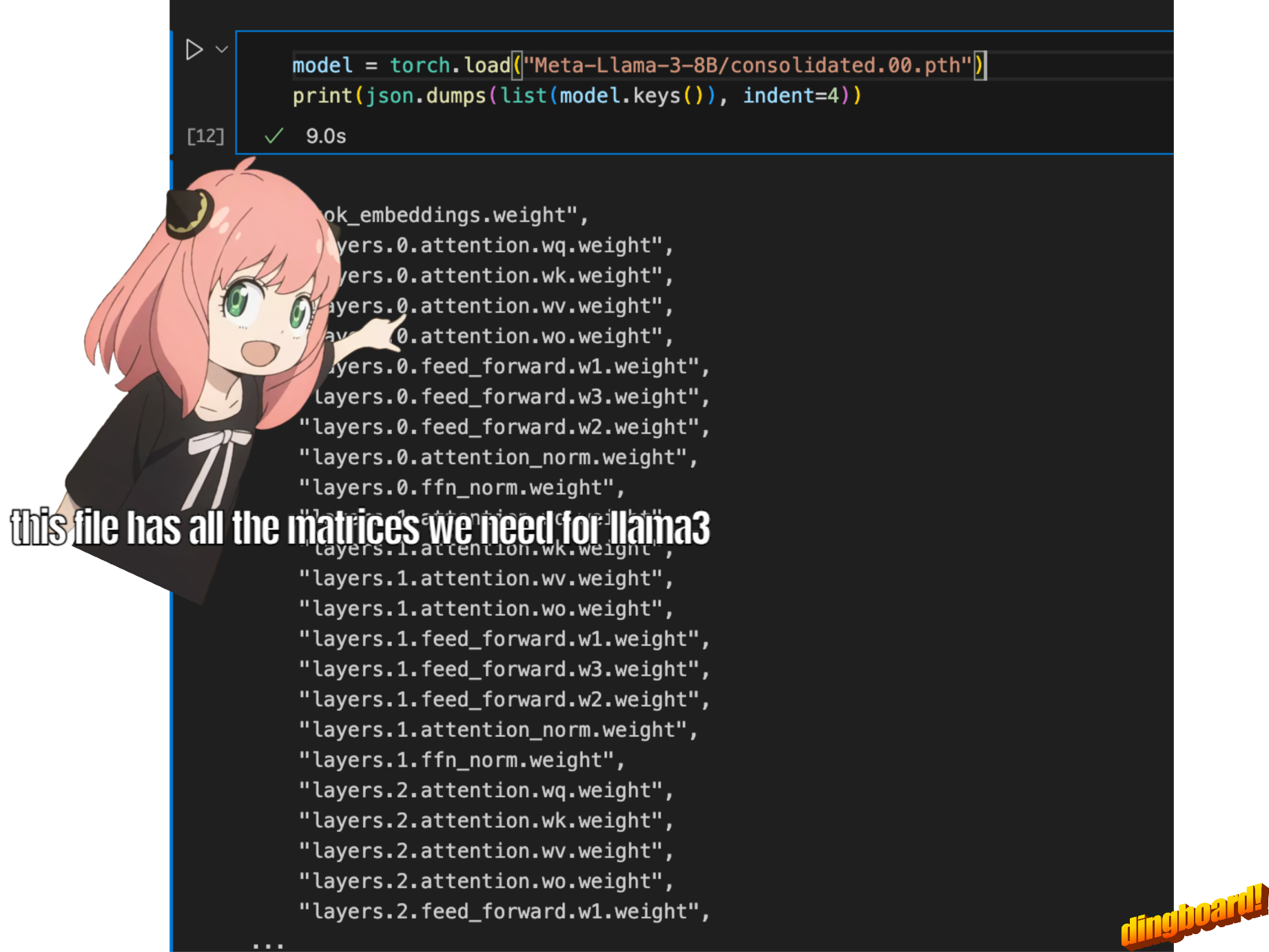
model = torch . load ( "Meta-Llama-3-8B/consolidated.00.pth" )
print ( json . dumps ( list ( model . keys ())[: 20 ], indent = 4 )) [
"tok_embeddings.weight",
"layers.0.attention.wq.weight",
"layers.0.attention.wk.weight",
"layers.0.attention.wv.weight",
"layers.0.attention.wo.weight",
"layers.0.feed_forward.w1.weight",
"layers.0.feed_forward.w3.weight",
"layers.0.feed_forward.w2.weight",
"layers.0.attention_norm.weight",
"layers.0.ffn_norm.weight",
"layers.1.attention.wq.weight",
"layers.1.attention.wk.weight",
"layers.1.attention.wv.weight",
"layers.1.attention.wo.weight",
"layers.1.feed_forward.w1.weight",
"layers.1.feed_forward.w3.weight",
"layers.1.feed_forward.w2.weight",
"layers.1.attention_norm.weight",
"layers.1.ffn_norm.weight",
"layers.2.attention.wq.weight"
]
with open ( "Meta-Llama-3-8B/params.json" , "r" ) as f :
config = json . load ( f )
config {'dim': 4096,
'n_layers': 32,
'n_heads': 32,
'n_kv_heads': 8,
'vocab_size': 128256,
'multiple_of': 1024,
'ffn_dim_multiplier': 1.3,
'norm_eps': 1e-05,
'rope_theta': 500000.0}
dim = config [ "dim" ]
n_layers = config [ "n_layers" ]
n_heads = config [ "n_heads" ]
n_kv_heads = config [ "n_kv_heads" ]
vocab_size = config [ "vocab_size" ]
multiple_of = config [ "multiple_of" ]
ffn_dim_multiplier = config [ "ffn_dim_multiplier" ]
norm_eps = config [ "norm_eps" ]
rope_theta = torch . tensor ( config [ "rope_theta" ])aquí usamos tiktoken (creo que una biblioteca openai) como tokenizador
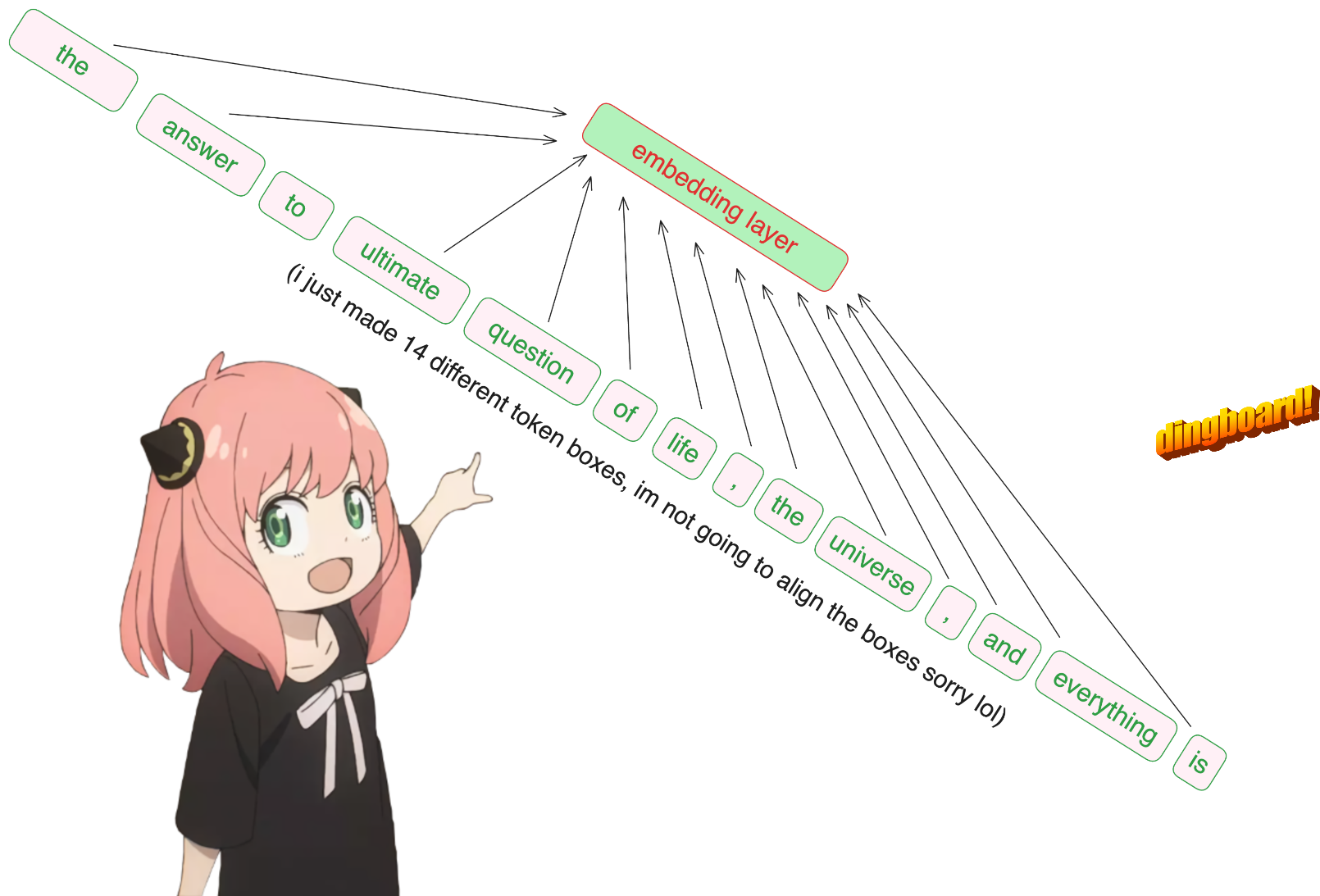
prompt = "the answer to the ultimate question of life, the universe, and everything is "
tokens = [ 128000 ] + tokenizer . encode ( prompt )
print ( tokens )
tokens = torch . tensor ( tokens )
prompt_split_as_tokens = [ tokenizer . decode ([ token . item ()]) for token in tokens ]
print ( prompt_split_as_tokens ) [128000, 1820, 4320, 311, 279, 17139, 3488, 315, 2324, 11, 279, 15861, 11, 323, 4395, 374, 220]
['<|begin_of_text|>', 'the', ' answer', ' to', ' the', ' ultimate', ' question', ' of', ' life', ',', ' the', ' universe', ',', ' and', ' everything', ' is', ' ']
LO SIENTO, pero esta es la única parte del código base donde utilizo un módulo de red neuronal incorporado.
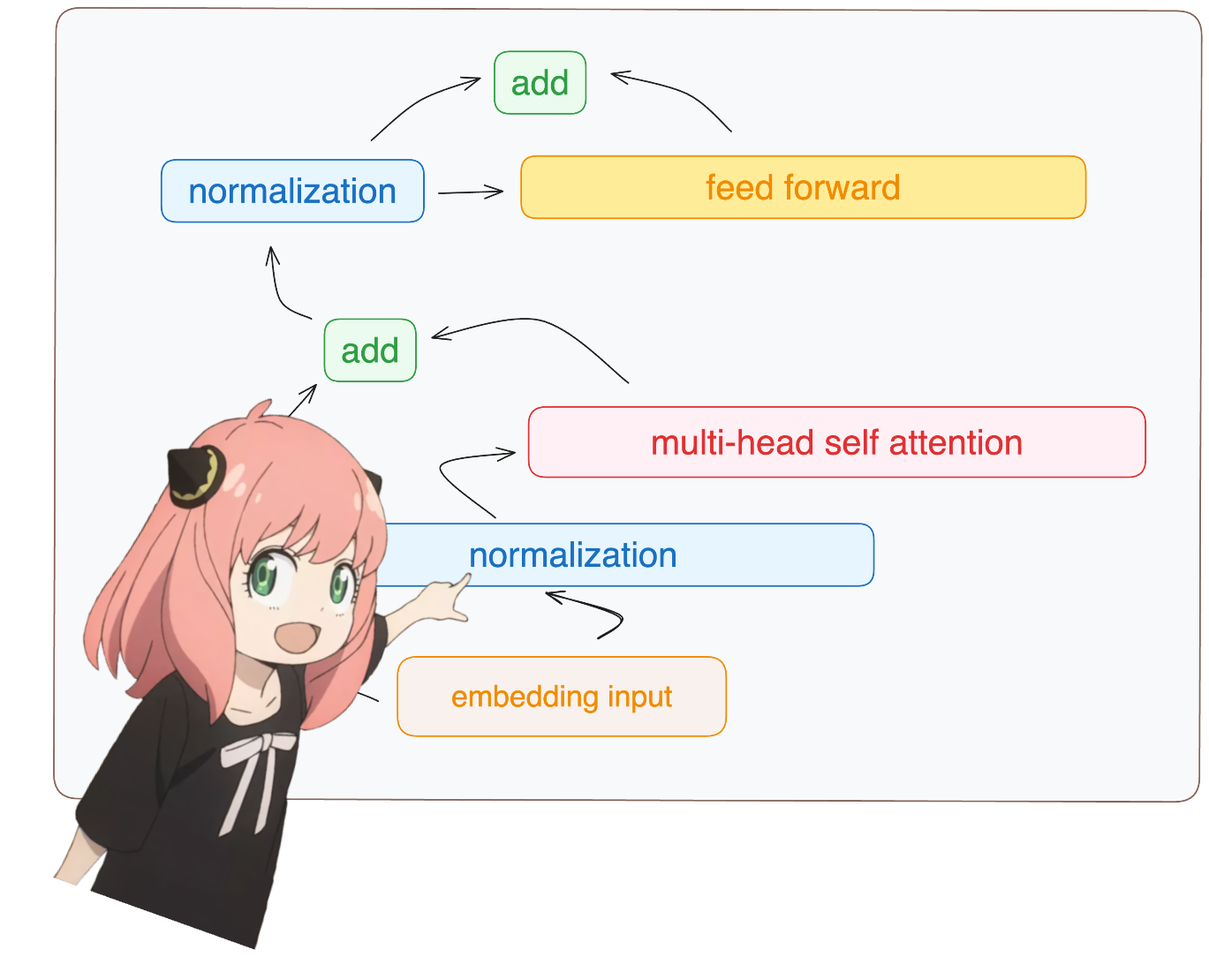
de todos modos, nuestros tokens [17x1] ahora son [17x4096], es decir, 17 incrustaciones (una para cada token) de longitud 4096
nota: realiza un seguimiento de las formas, hace que sea mucho más fácil entender todo

embedding_layer = torch . nn . Embedding ( vocab_size , dim )
embedding_layer . weight . data . copy_ ( model [ "tok_embeddings.weight" ])
token_embeddings_unnormalized = embedding_layer ( tokens ). to ( torch . bfloat16 )
token_embeddings_unnormalized . shape torch.Size([17, 4096])
Por favor, tenga en cuenta que después de este paso las formas no cambian, los valores simplemente se normalizan.
cosas a tener en cuenta, necesitamos un norm_eps (de config) porque no queremos establecer accidentalmente rms en 0 y dividir por 0
aquí está la fórmula:

# def rms_norm(tensor, norm_weights):
# rms = (tensor.pow(2).mean(-1, keepdim=True) + norm_eps)**0.5
# return tensor * (norm_weights / rms)
def rms_norm ( tensor , norm_weights ):
return ( tensor * torch . rsqrt ( tensor . pow ( 2 ). mean ( - 1 , keepdim = True ) + norm_eps )) * norm_weights me verás accediendo a la capa.0 desde el dictado del modelo (esta es la primera capa)
de todos modos, después de normalizar nuestras formas siguen siendo [17x4096] iguales que incrustadas pero normalizadas
token_embeddings = rms_norm ( token_embeddings_unnormalized , model [ "layers.0.attention_norm.weight" ])
token_embeddings . shape torch.Size([17, 4096])
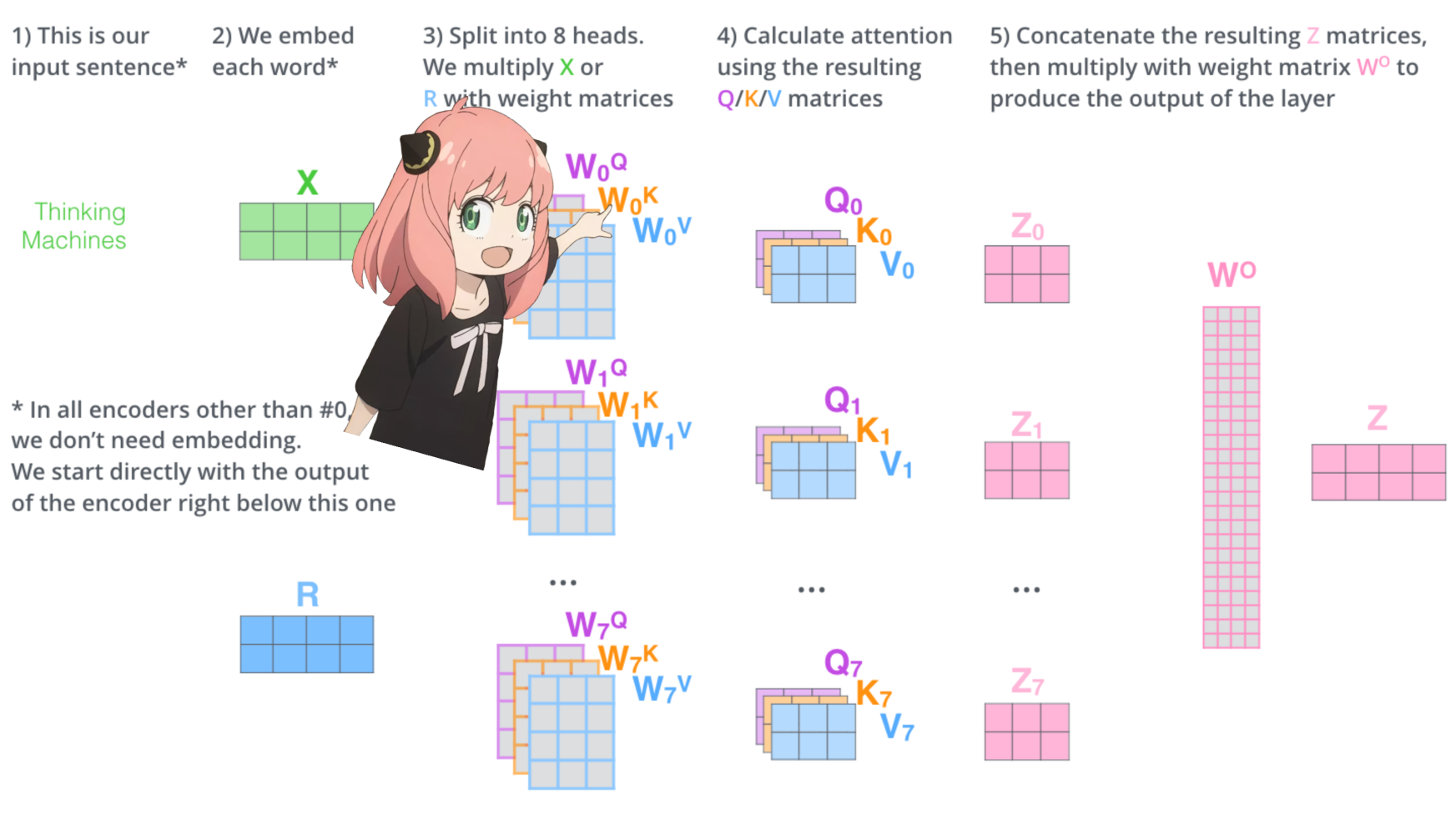
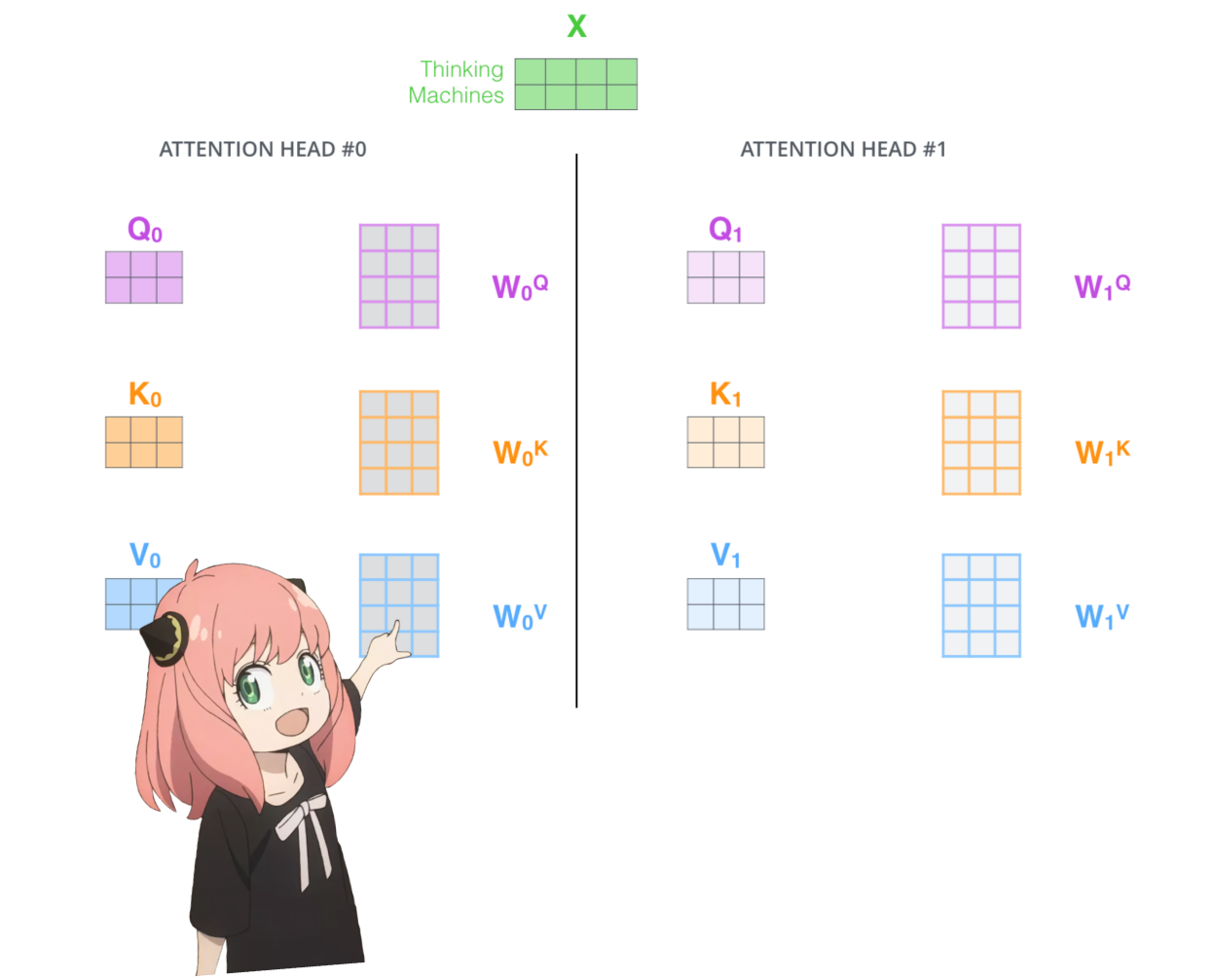
carguemos los cabezales de atención de la primera capa del transformador
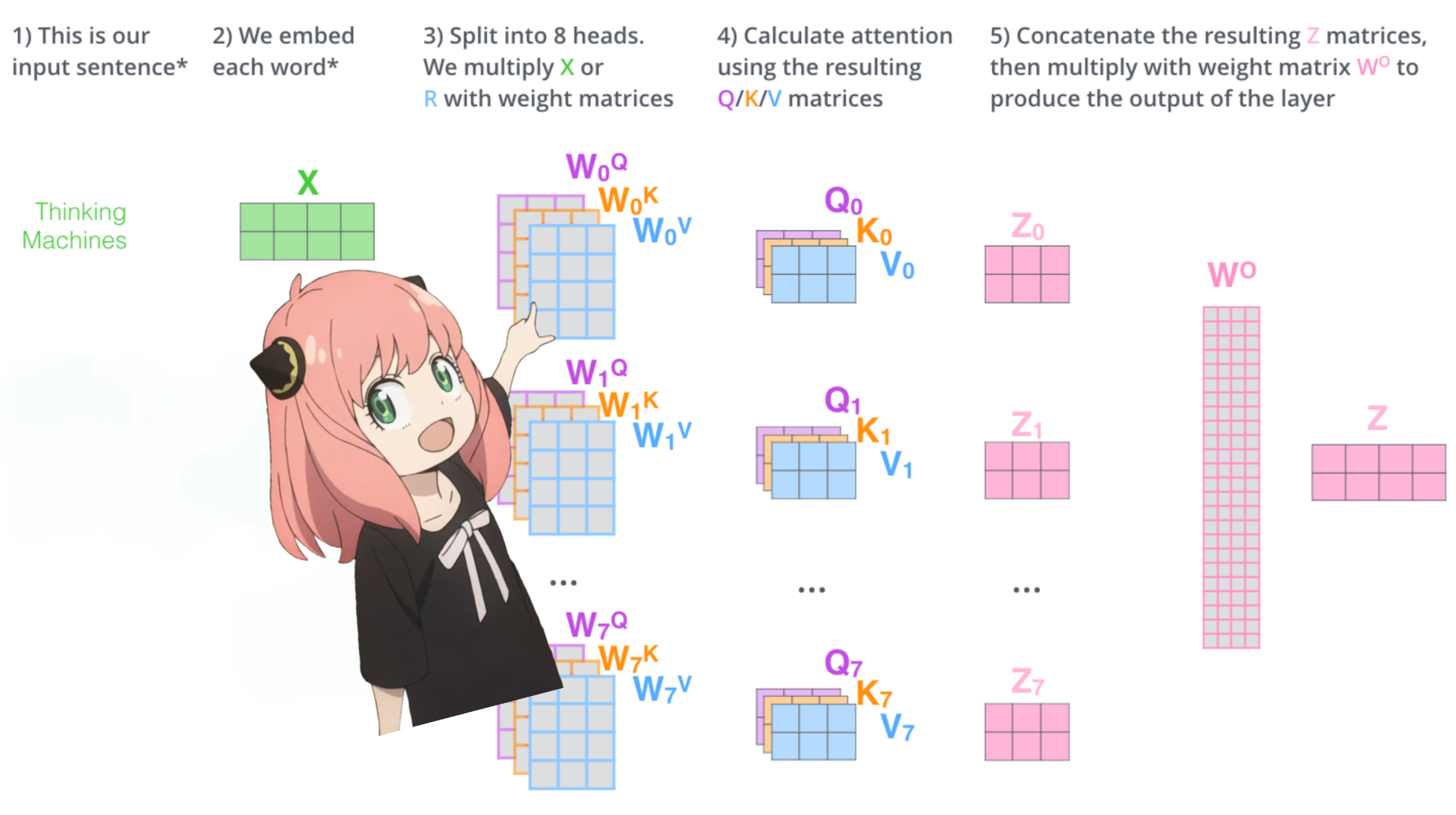
> cuando cargamos los vectores de consulta, clave, valor y salida del modelo, notamos que las formas son [4096x4096], [1024x4096], [1024x4096], [4096x4096]
> a primera vista esto es extraño porque idealmente queremos cada q,k,v y o para cada cabeza individualmente
> los autores del código los agruparon porque es fácil y ayuda a paralizar la multiplicación de cabezas de atención.
> voy a desenvolver todo...
print (
model [ "layers.0.attention.wq.weight" ]. shape ,
model [ "layers.0.attention.wk.weight" ]. shape ,
model [ "layers.0.attention.wv.weight" ]. shape ,
model [ "layers.0.attention.wo.weight" ]. shape
) torch.Size([4096, 4096]) torch.Size([1024, 4096]) torch.Size([1024, 4096]) torch.Size([4096, 4096])
en la siguiente sección desenvolveremos las consultas de múltiples cabezas de atención, la forma resultante es [32x128x4096]
aquí, 32 es el número de cabezas de atención en llama3, 128 es el tamaño del vector de consulta y 4096 es el tamaño del token incrustado.
q_layer0 = model [ "layers.0.attention.wq.weight" ]
head_dim = q_layer0 . shape [ 0 ] // n_heads
q_layer0 = q_layer0 . view ( n_heads , head_dim , dim )
q_layer0 . shape torch.Size([32, 128, 4096])
aquí accedo al primer encabezado de la matriz de peso de consulta de la primera capa, el tamaño de esta matriz de peso de consulta es [128x4096]
q_layer0_head0 = q_layer0 [ 0 ]
q_layer0_head0 . shape torch.Size([128, 4096])
Aquí puedes ver que la forma resultante es [17x128], esto se debe a que tenemos 17 tokens y para cada token hay una consulta de 128 de longitud.

q_per_token = torch . matmul ( token_embeddings , q_layer0_head0 . T )
q_per_token . shape torch.Size([17, 128])
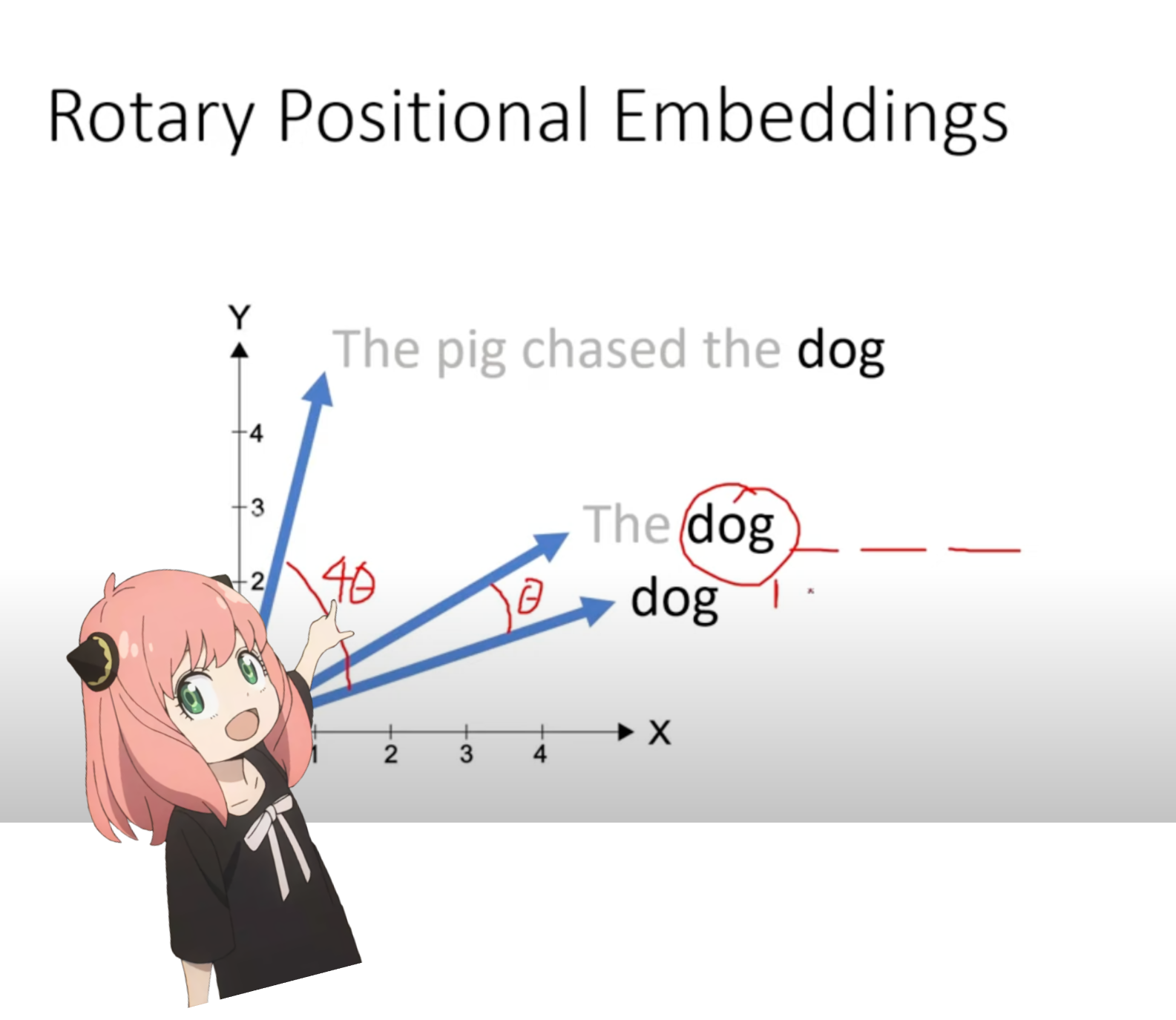
Ahora estamos en una etapa en la que tenemos un vector de consulta para cada token en nuestro mensaje, pero si lo piensas bien, el vector de consulta individual no tiene idea de la posición en el mensaje.
consulta: "la respuesta a la pregunta fundamental sobre la vida, el universo y todo es "
en nuestro mensaje hemos usado "the" tres veces, necesitamos que los vectores de consulta de los 3 tokens "the" tengan diferentes vectores de consulta (cada uno de tamaño [1x128]) según sus posiciones en la consulta. Realizamos estas rotaciones utilizando RoPE (incrustación posicional rotatoria).
Mira este video (esto es lo que vi) para entender las matemáticas. https://www.youtube.com/watch?v=o29P0Kpobz0&t=530s
q_per_token_split_into_pairs = q_per_token . float (). view ( q_per_token . shape [ 0 ], - 1 , 2 )
q_per_token_split_into_pairs . shape torch.Size([17, 64, 2])
En el paso anterior, dividimos los vectores de consulta en pares y aplicamos un desplazamiento del ángulo de rotación a cada par.
Ahora tenemos un vector de tamaño [17x64x2], ¡estas son las 128 consultas de longitud divididas en 64 pares para cada token en el mensaje! ¡cada uno de esos 64 pares será rotado por m*(theta) donde m es la posición del token para el cual estamos rotando la consulta!

zero_to_one_split_into_64_parts = torch . tensor ( range ( 64 )) / 64
zero_to_one_split_into_64_parts tensor([0.0000, 0.0156, 0.0312, 0.0469, 0.0625, 0.0781, 0.0938, 0.1094, 0.1250,
0.1406, 0.1562, 0.1719, 0.1875, 0.2031, 0.2188, 0.2344, 0.2500, 0.2656,
0.2812, 0.2969, 0.3125, 0.3281, 0.3438, 0.3594, 0.3750, 0.3906, 0.4062,
0.4219, 0.4375, 0.4531, 0.4688, 0.4844, 0.5000, 0.5156, 0.5312, 0.5469,
0.5625, 0.5781, 0.5938, 0.6094, 0.6250, 0.6406, 0.6562, 0.6719, 0.6875,
0.7031, 0.7188, 0.7344, 0.7500, 0.7656, 0.7812, 0.7969, 0.8125, 0.8281,
0.8438, 0.8594, 0.8750, 0.8906, 0.9062, 0.9219, 0.9375, 0.9531, 0.9688,
0.9844])
freqs = 1.0 / ( rope_theta ** zero_to_one_split_into_64_parts )
freqs tensor([1.0000e+00, 8.1462e-01, 6.6360e-01, 5.4058e-01, 4.4037e-01, 3.5873e-01,
2.9223e-01, 2.3805e-01, 1.9392e-01, 1.5797e-01, 1.2869e-01, 1.0483e-01,
8.5397e-02, 6.9566e-02, 5.6670e-02, 4.6164e-02, 3.7606e-02, 3.0635e-02,
2.4955e-02, 2.0329e-02, 1.6560e-02, 1.3490e-02, 1.0990e-02, 8.9523e-03,
7.2927e-03, 5.9407e-03, 4.8394e-03, 3.9423e-03, 3.2114e-03, 2.6161e-03,
2.1311e-03, 1.7360e-03, 1.4142e-03, 1.1520e-03, 9.3847e-04, 7.6450e-04,
6.2277e-04, 5.0732e-04, 4.1327e-04, 3.3666e-04, 2.7425e-04, 2.2341e-04,
1.8199e-04, 1.4825e-04, 1.2077e-04, 9.8381e-05, 8.0143e-05, 6.5286e-05,
5.3183e-05, 4.3324e-05, 3.5292e-05, 2.8750e-05, 2.3420e-05, 1.9078e-05,
1.5542e-05, 1.2660e-05, 1.0313e-05, 8.4015e-06, 6.8440e-06, 5.5752e-06,
4.5417e-06, 3.6997e-06, 3.0139e-06, 2.4551e-06])
freqs_for_each_token = torch . outer ( torch . arange ( 17 ), freqs )
freqs_cis = torch . polar ( torch . ones_like ( freqs_for_each_token ), freqs_for_each_token )
freqs_cis . shape
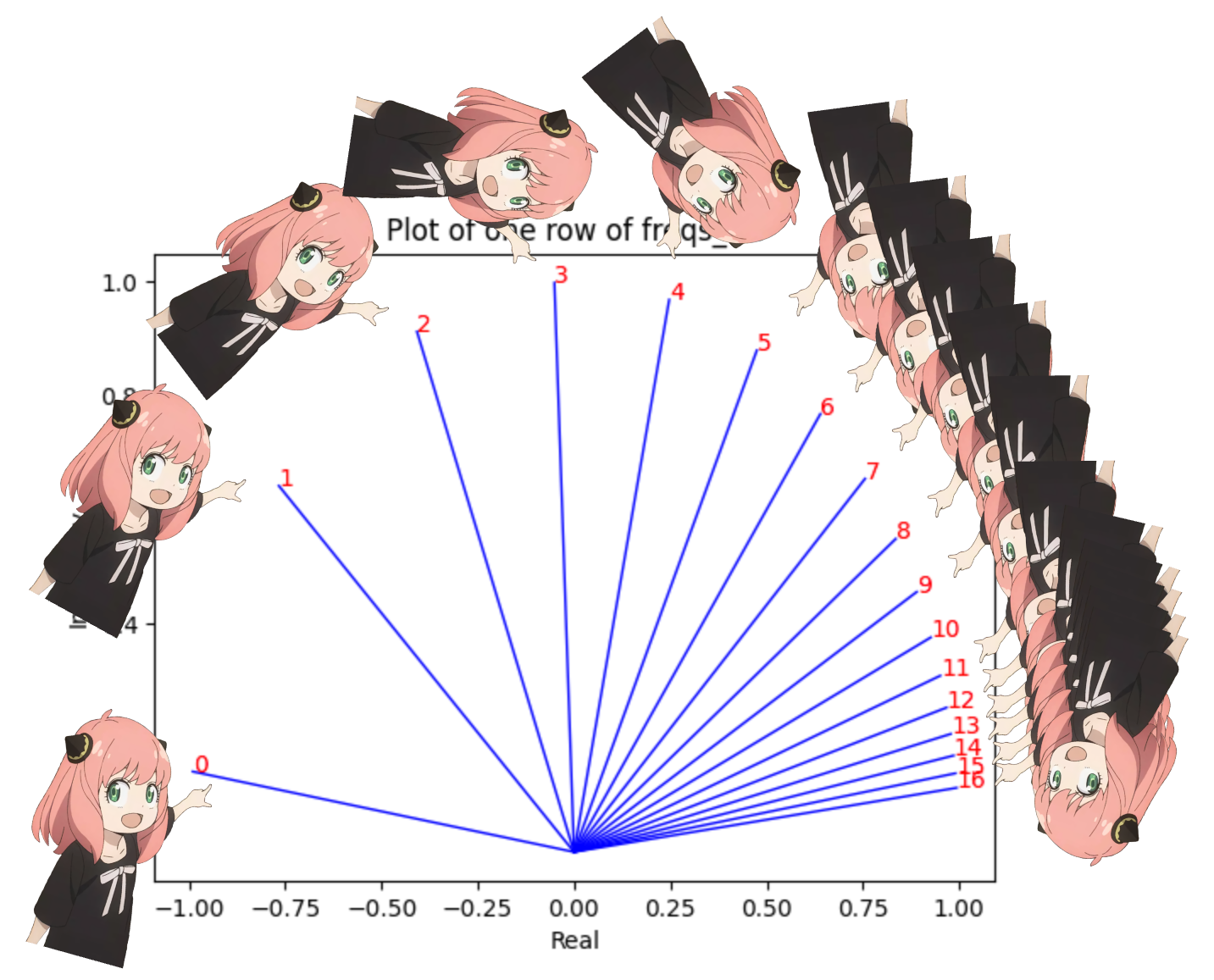
# viewing tjhe third row of freqs_cis
value = freqs_cis [ 3 ]
plt . figure ()
for i , element in enumerate ( value [: 17 ]):
plt . plot ([ 0 , element . real ], [ 0 , element . imag ], color = 'blue' , linewidth = 1 , label = f"Index: { i } " )
plt . annotate ( f" { i } " , xy = ( element . real , element . imag ), color = 'red' )
plt . xlabel ( 'Real' )
plt . ylabel ( 'Imaginary' )
plt . title ( 'Plot of one row of freqs_cis' )
plt . show ()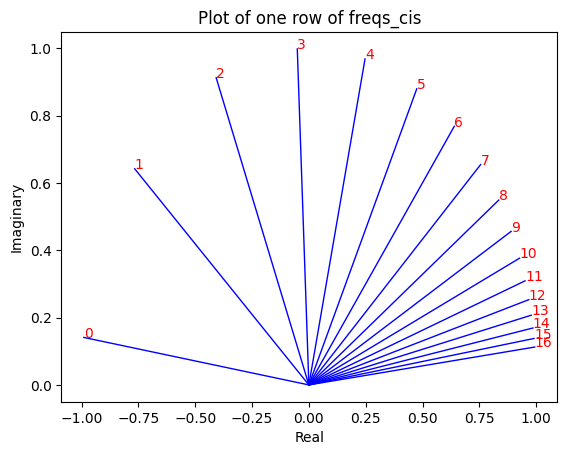
podemos convertir nuestras consultas (la que dividimos en pares) como números complejos y luego producto escalar para rotar la consulta según la posición
Honestamente, es hermoso pensar en esto :)
q_per_token_as_complex_numbers = torch . view_as_complex ( q_per_token_split_into_pairs )
q_per_token_as_complex_numbers . shape torch.Size([17, 64])
q_per_token_as_complex_numbers_rotated = q_per_token_as_complex_numbers * freqs_cis
q_per_token_as_complex_numbers_rotated . shape torch.Size([17, 64])
Podemos recuperar nuestras consultas como pares viendo los números complejos como números reales nuevamente.
q_per_token_split_into_pairs_rotated = torch . view_as_real ( q_per_token_as_complex_numbers_rotated )
q_per_token_split_into_pairs_rotated . shape torch.Size([17, 64, 2])
los pares rotados ahora están fusionados, ahora tenemos un nuevo vector de consulta (vector de consulta rotado) que tiene la forma [17x128] donde 17 es el número de tokens y 128 es la intensidad del vector de consulta
q_per_token_rotated = q_per_token_split_into_pairs_rotated . view ( q_per_token . shape )
q_per_token_rotated . shape torch.Size([17, 128])
k_layer0 = model [ "layers.0.attention.wk.weight" ]
k_layer0 = k_layer0 . view ( n_kv_heads , k_layer0 . shape [ 0 ] // n_kv_heads , dim )
k_layer0 . shape torch.Size([8, 128, 4096])
k_layer0_head0 = k_layer0 [ 0 ]
k_layer0_head0 . shape torch.Size([128, 4096])
k_per_token = torch . matmul ( token_embeddings , k_layer0_head0 . T )
k_per_token . shape torch.Size([17, 128])
k_per_token_split_into_pairs = k_per_token . float (). view ( k_per_token . shape [ 0 ], - 1 , 2 )
k_per_token_split_into_pairs . shape torch.Size([17, 64, 2])
k_per_token_as_complex_numbers = torch . view_as_complex ( k_per_token_split_into_pairs )
k_per_token_as_complex_numbers . shape torch.Size([17, 64])
k_per_token_split_into_pairs_rotated = torch . view_as_real ( k_per_token_as_complex_numbers * freqs_cis )
k_per_token_split_into_pairs_rotated . shape torch.Size([17, 64, 2])
k_per_token_rotated = k_per_token_split_into_pairs_rotated . view ( k_per_token . shape )
k_per_token_rotated . shape torch.Size([17, 128])
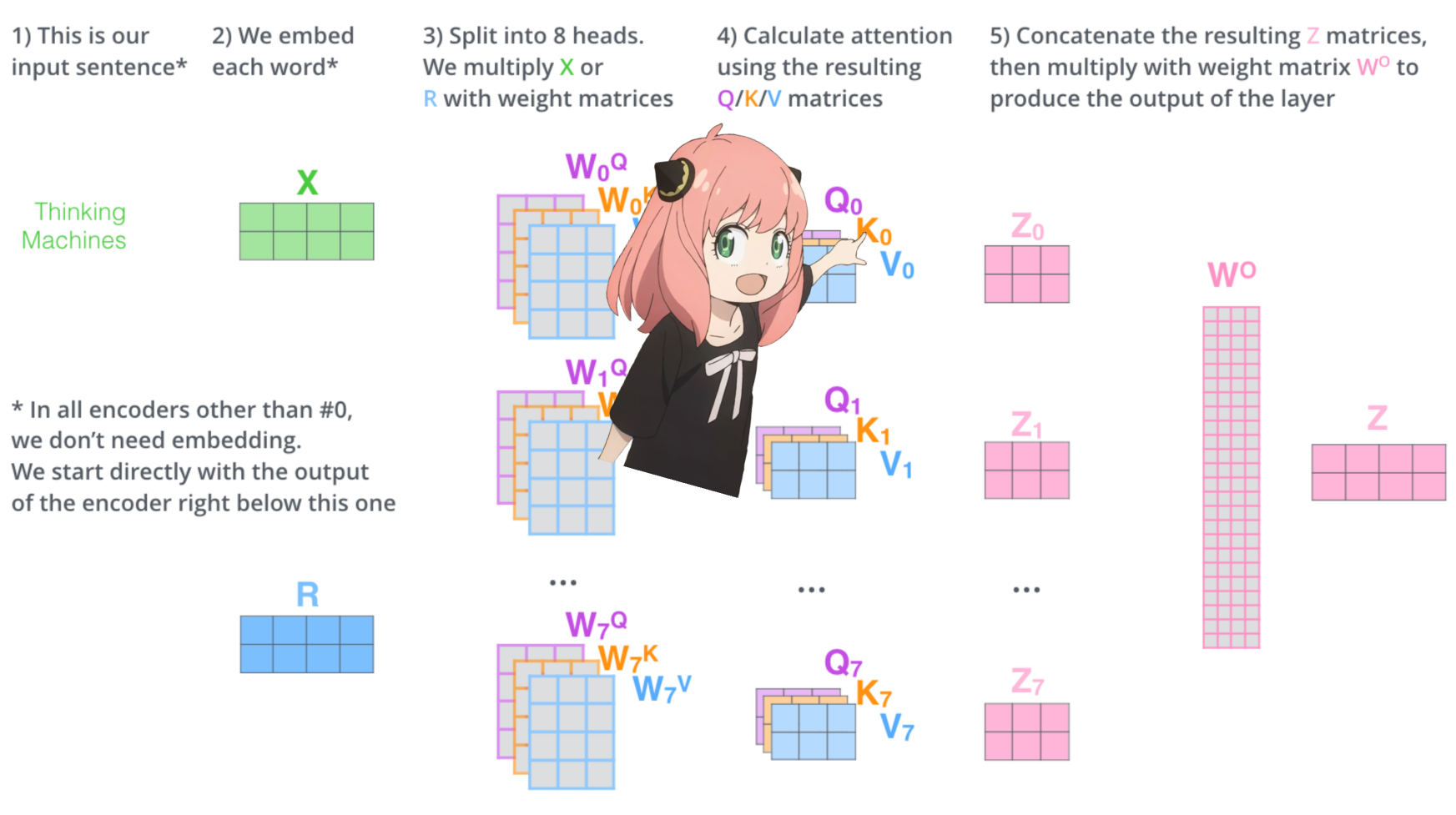
Hacer esto nos dará una puntuación que asignará cada token entre sí.
esta puntuación describe qué tan bien se relaciona la consulta de cada token con la clave de cada token. ESTO ES AUTOATENCIÓN :)
la forma de la matriz de puntuación de atención (qk_per_token) es [17x17] donde 17 es el número de tokens en el mensaje
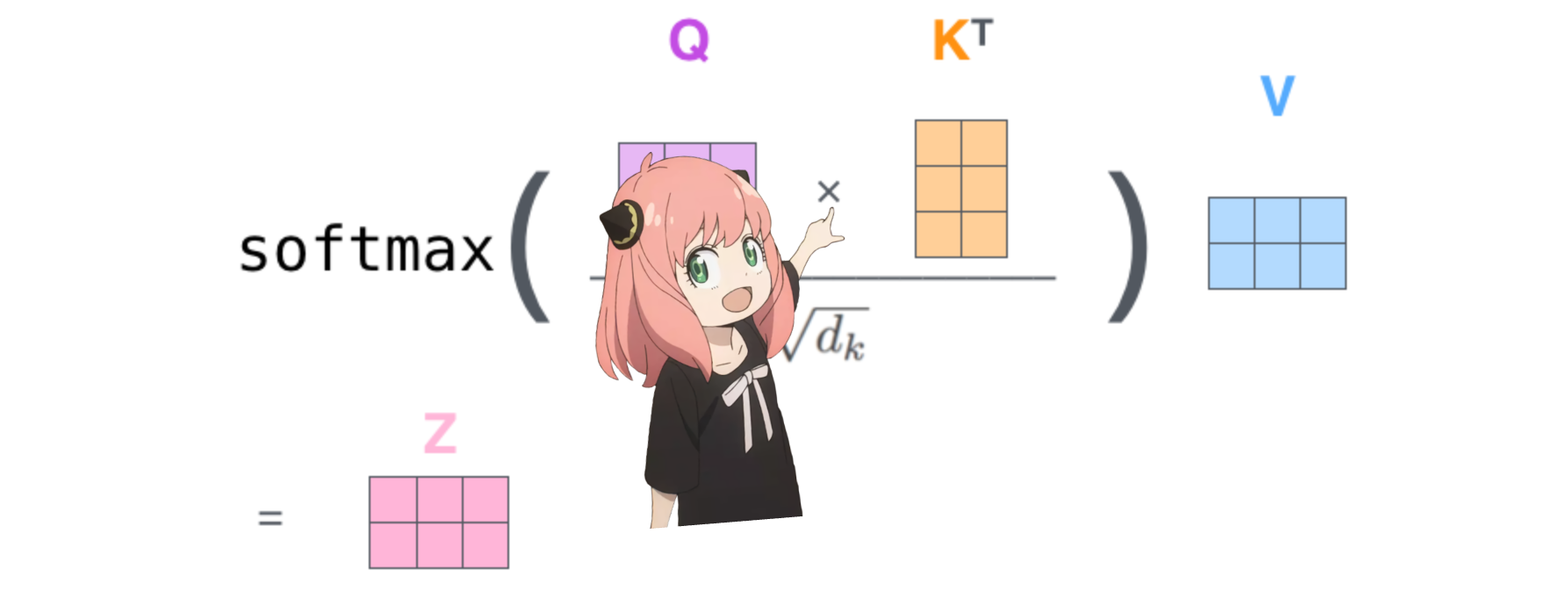
qk_per_token = torch . matmul ( q_per_token_rotated , k_per_token_rotated . T ) / ( head_dim ) ** 0.5
qk_per_token . shape torch.Size([17, 17])
Durante el proceso de entrenamiento de llama3, las puntuaciones futuras del token qk están enmascaradas.
¿por qué? porque durante el entrenamiento solo aprendemos a predecir tokens usando tokens pasados.
como resultado, durante la inferencia fijamos los tokens futuros en cero.
def display_qk_heatmap ( qk_per_token ):
_ , ax = plt . subplots ()
im = ax . imshow ( qk_per_token . to ( float ). detach (), cmap = 'viridis' )
ax . set_xticks ( range ( len ( prompt_split_as_tokens )))
ax . set_yticks ( range ( len ( prompt_split_as_tokens )))
ax . set_xticklabels ( prompt_split_as_tokens )
ax . set_yticklabels ( prompt_split_as_tokens )
ax . figure . colorbar ( im , ax = ax )
display_qk_heatmap ( qk_per_token )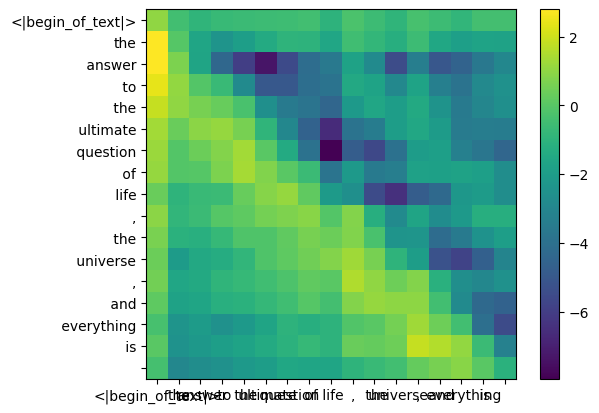
mask = torch . full (( len ( tokens ), len ( tokens )), float ( "-inf" ), device = tokens . device )
mask = torch . triu ( mask , diagonal = 1 )
mask tensor([[0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]])
qk_per_token_after_masking = qk_per_token + mask
display_qk_heatmap ( qk_per_token_after_masking )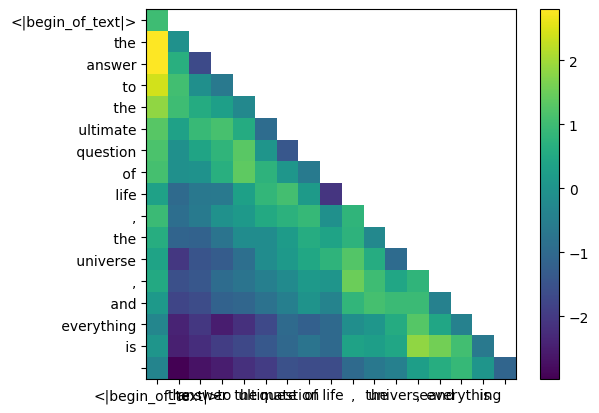
qk_per_token_after_masking_after_softmax = torch . nn . functional . softmax ( qk_per_token_after_masking , dim = 1 ). to ( torch . bfloat16 )
display_qk_heatmap ( qk_per_token_after_masking_after_softmax )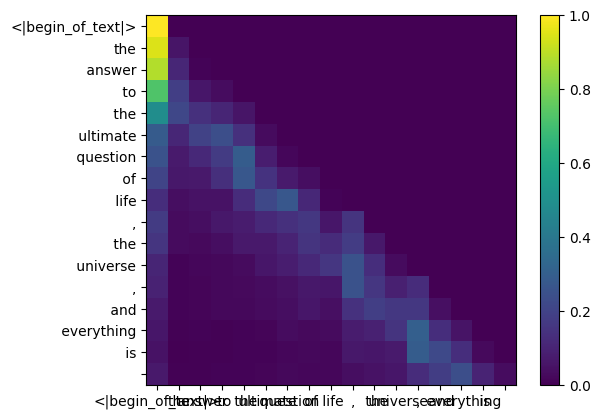
v_layer0 = model [ "layers.0.attention.wv.weight" ]
v_layer0 = v_layer0 . view ( n_kv_heads , v_layer0 . shape [ 0 ] // n_kv_heads , dim )
v_layer0 . shape torch.Size([8, 128, 4096])
la primera capa, la primera matriz de peso del valor de la cabeza se proporciona a continuación
v_layer0_head0 = v_layer0 [ 0 ]
v_layer0_head0 . shape torch.Size([128, 4096])
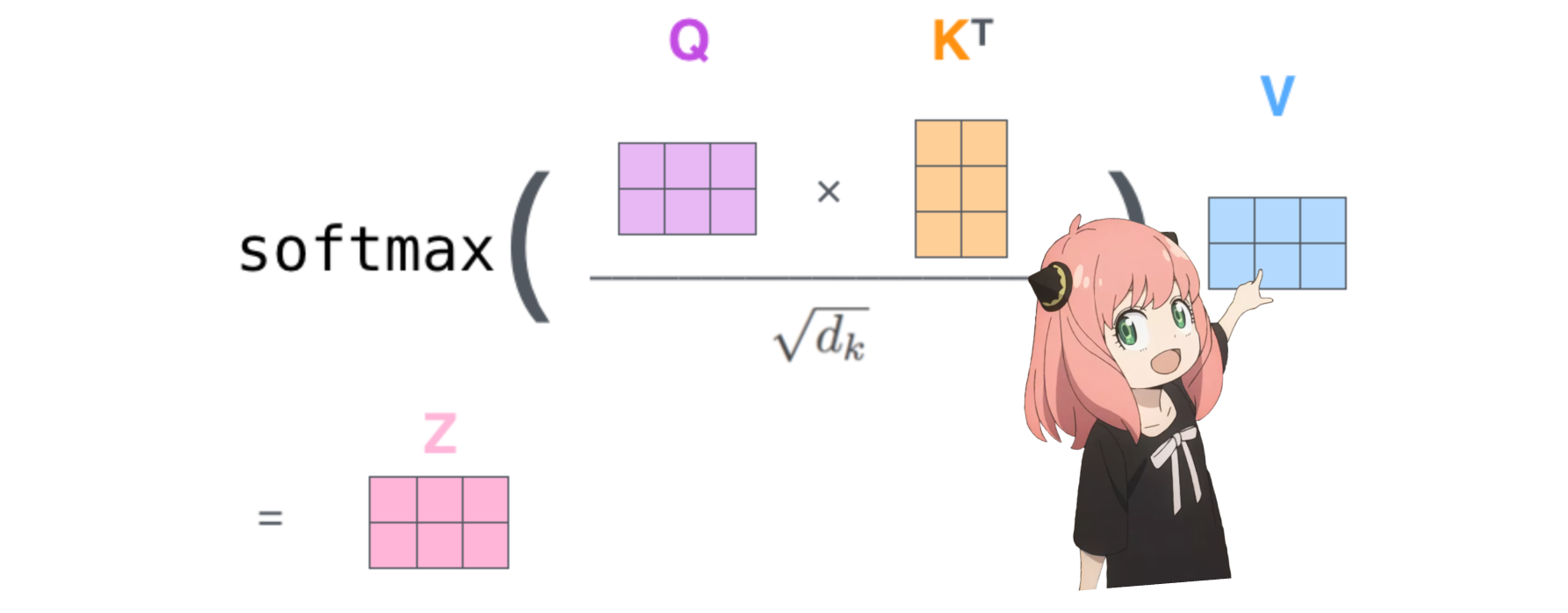
v_per_token = torch . matmul ( token_embeddings , v_layer0_head0 . T )
v_per_token . shape torch.Size([17, 128])
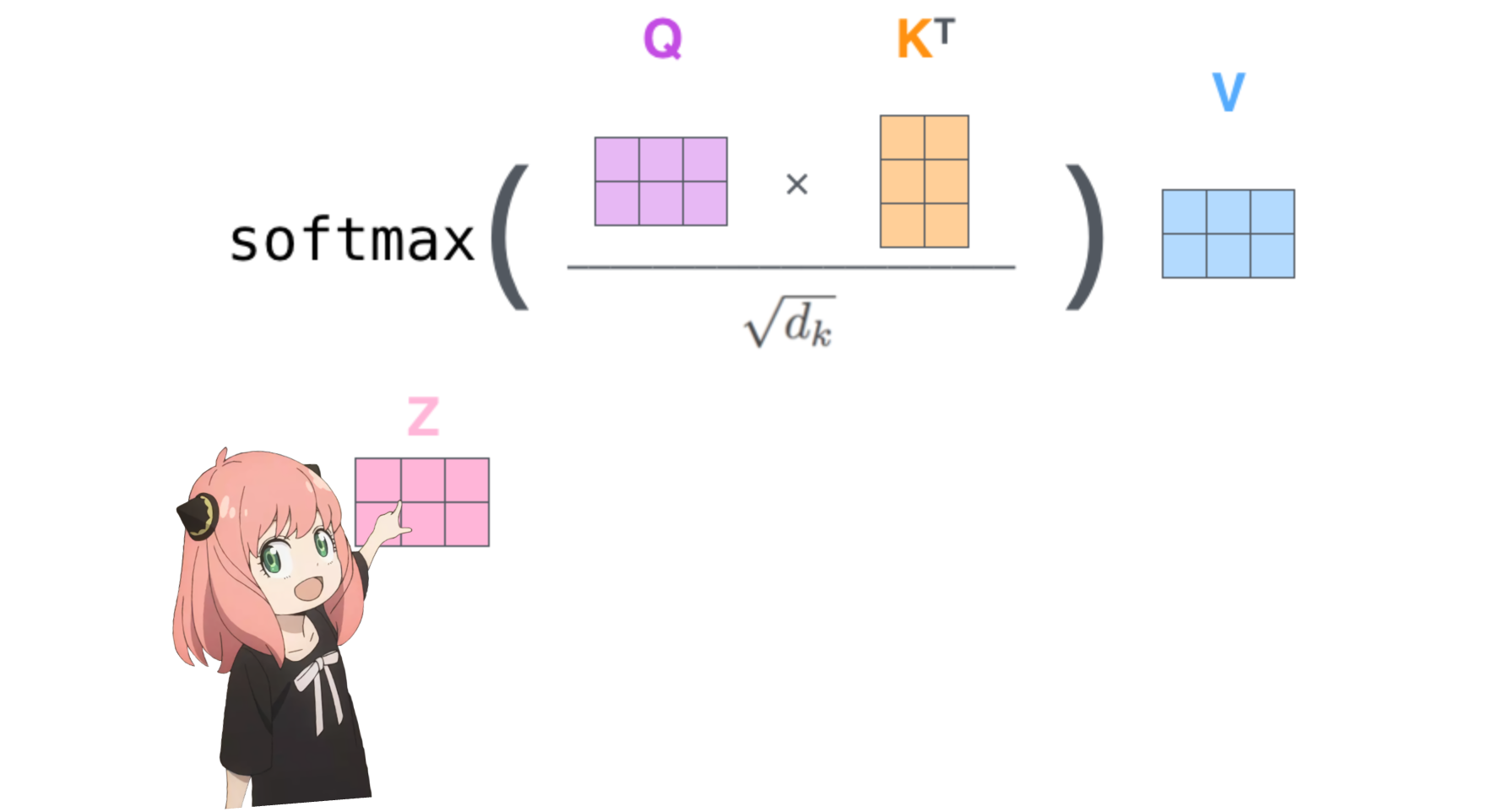
qkv_attention = torch . matmul ( qk_per_token_after_masking_after_softmax , v_per_token )
qkv_attention . shape torch.Size([17, 128])
