greta.gam le permite utilizar las funciones más fluidas y la sintaxis de fórmulas de mgcv para definir términos fluidos para su uso en un modelo greta. Luego puede definir su propia probabilidad de completar el modelo y ajustarlo mediante MCMC.
¡Este es un trabajo en progreso!
A continuación se muestra un ejemplo sencillo adaptado del archivo de ayuda mgcv ?gam :
En mgcv :
library( mgcv )
# > Loading required package: nlme
# > This is mgcv 1.9-1. For overview type 'help("mgcv-package")'.
set.seed( 2 )
# simulate some data...
dat <- gamSim( 1 , n = 400 , dist = " normal " , scale = 0.3 )
# > Gu & Wahba 4 term additive model
# fit a model using gam()
b <- gam( y ~ s( x2 ), data = dat ) Ahora ajustando el mismo modelo en greta :
library( greta.gam )
# > Loading required package: greta
# >
# > Attaching package: 'greta'
# > The following objects are masked from 'package:stats':
# >
# > binomial, cov2cor, poisson
# > The following objects are masked from 'package:base':
# >
# > %*%, apply, backsolve, beta, chol2inv, colMeans, colSums, diag,
# > eigen, forwardsolve, gamma, identity, rowMeans, rowSums, sweep,
# > tapply
set.seed( 2024 - 02 - 09 )
# setup the linear predictor for the smooth
z <- smooths( ~ s( x2 ), data = dat )
# > ℹ Initialising python and checking dependencies, this may take a moment.
# > ✔ Initialising python and checking dependencies ... done!
# set the distribution of the response
distribution( dat $ y ) <- normal( z , 1 )
# make some prediction data
pred_dat <- data.frame ( x2 = seq( 0 , 1 , length.out = 100 ))
# z_pred stores the predictions
z_pred <- evaluate_smooths( z , newdata = pred_dat )
# build model
m <- model( z_pred )
# draw from the posterior
draws <- mcmc( m , n_samples = 200 )
# > running 4 chains simultaneously on up to 8 CPU cores
#> warmup 0/1000 | eta: ?s warmup == 50/1000 | eta: 30s warmup ==== 100/1000 | eta: 17s warmup ====== 150/1000 | eta: 12s warmup ======== 200/1000 | eta: 10s warmup ========== 250/1000 | eta: 8s warmup =========== 300/1000 | eta: 7s warmup ============= 350/1000 | eta: 6s warmup =============== 400/1000 | eta: 5s warmup ================= 450/1000 | eta: 5s warmup =================== 500/1000 | eta: 4s warmup ===================== 550/1000 | eta: 4s warmup ======================= 600/1000 | eta: 3s warmup ========================= 650/1000 | eta: 3s warmup =========================== 700/1000 | eta: 2s warmup ============================ 750/1000 | eta: 2s warmup ============================== 800/1000 | eta: 1s warmup ================================ 850/1000 | eta: 1s warmup ================================== 900/1000 | eta: 1s warmup ==================================== 950/1000 | eta: 0s warmup ====================================== 1000/1000 | eta: 0s
# > sampling 0/200 | eta: ?s sampling ========== 50/200 | eta: 1s sampling =================== 100/200 | eta: 0s sampling ============================ 150/200 | eta: 0s sampling ====================================== 200/200 | eta: 0s
# plot the mgcv fit
plot( b , scheme = 1 , shift = coef( b )[ 1 ])
# add in a line for each posterior sample
apply( draws [[ 1 ]], 1 , lines , x = pred_dat $ x2 , col = " blue " )
# > NULL
# plot the data
points( dat $ x2 , dat $ y , pch = 19 , cex = 0.2 )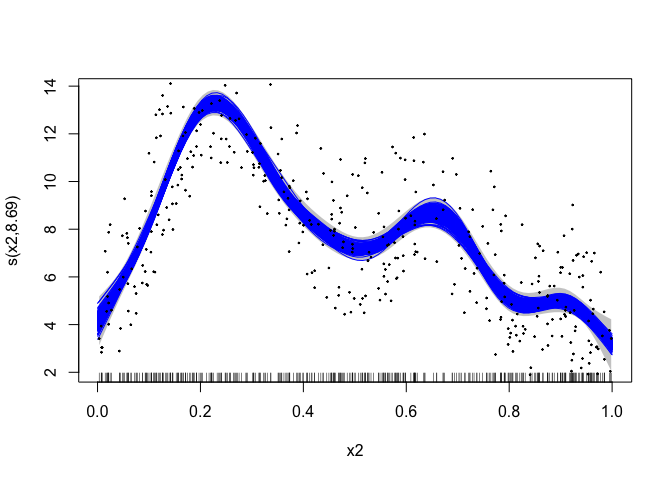
greta.gam utiliza algunos trucos de la rutina jagam (Wood, 2016) en mgcv para que todo funcione. Aquí hay algunos breves detalles para aquellos interesados en el funcionamiento interno...
Los GAM son modelos con interpretaciones bayesianas (incluso cuando se ajustan utilizando métodos “frecuentistas”). Se puede pensar en la matriz de penalización más suave como una matriz de precisión previa en un modelo bayesiano de efectos aleatorios. Las matrices de diseño se construyen exactamente como en el caso frecuentista. Consulte Miller (2021) para obtener más información sobre esto.
Existe una ligera dificultad en la interpretación bayesiana del GAM en el sentido de que, en su forma ingenua, los priors son inadecuados como espacio nulo de la penalización (en el caso 1D, generalmente el término lineal). Para obtener antecedentes adecuados podemos utilizar uno de los “trucos” empleados en Marra y Wood (2011): penalizar de alguna manera las partes de la penalización que conducen a antecedentes inadecuados. Tomamos la opción proporcionada por jagam y creamos una matriz de penalización adicional para estos términos (a partir de una descomposición propia de la matriz de penalización; ver Marra & Wood, 2011).
Marra, G y Wood, SN (2011) Selección práctica de variables para modelos aditivos generalizados. Estadística computacional y análisis de datos, 55, 2372–2387.
Miller DL (2021). Vistas bayesianas del modelado aditivo generalizado. arXiv.
Wood, SN (2016) Solo otro modelador aditivo de Gibbs: interfaz entre JAGS y mgcv. Revista de software estadístico 75, no. 7