practico 1 series

visualbásico

1.0.0

Descargar

Practico 1 - Series

Practico de Series de la introduccion a la informatica con el ingeniero Mollo.

Lenguaje de Programación: Visual Basic
ver PDF del práctico

Contenido

Generar la tabla de multiplicar de n
Generar la división de n
Generar la suma de n
Generar la resta de n
Ejercicio 5
Ejercicio 6
Ejercicio 7
Ejercicio 8
Ejercicio 9
Ejercicio 10
Ejercicio 11
Ejercicio 12
Ejercicio 13
Ejercicio 14
Ejercicio 15

Ejercicio 1, 2, 3 y 4

ejercicio-1-2-3-4

Ejercicios 1,2,3,4. Generar la tabla de operaciones aritméticas de n... términos:

suma
resta
multiplación
división

Ver código

Public Function SelectTable(n As Double, operatorString As String) As String
  Dim result, symbol As String
  Dim index As Integer
  Dim res As Double
  result = "" : symbol = ""
  For index = 0 To 10
      Select Case operatorString
          Case "*"
              symbol = " *"
              res = (index * n)
          Case "/"
              symbol = " /"
              res = (index / n)
          Case "+"
              symbol = " +"
              res = (index + n)
          Case "-"
              symbol = " -"
              res = (index - n)
      End Select
      result = result + Str(index) + symbol + Str(n) + " = " + Str(res) + Chr(13) + Chr(10)
  Next
  Return result
End Function

# Output: SelectTable(TextBox1.Text, "+")
 0 + 5 =  5
 1 + 5 =  6
 2 + 5 =  7
 3 + 5 =  8
 4 + 5 =  9
 5 + 5 =  10
 6 + 5 =  11
 7 + 5 =  12
 8 + 5 =  13
 9 + 5 =  14
 10 + 5 =  15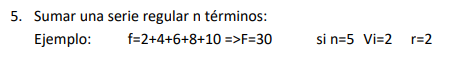

Ejercicio 5

ejercicio-5

Sumar una serie regular de n términos:

Ver código

Public Function RegularSerie(n As UInt16, initialValue As Single, razon As Single, sumTotal As Boolean) As String
    Dim result As String = ""
    Dim index As UInt32
    Dim t, total As Single
    For index = 1 To n
        t = initialValue + (index - 1) * razon
        If sumTotal Then
            total += t
            result = Str(total)
        Else
            If index = n Then
                result += Str(t)
            Else
                result = result + Str(t) + "  + "
            End If
        End If
    Next
    Return "F = " + result
End Function

# Output: RegularSerie(TextBox1.Text, TextBox2.Text, TextBox3.Text, True)
F = 30
# Output string: RegularSerie(TextBox1.Text, TextBox2.Text, TextBox3.Text, False)
F =  2  +  4  +  6  +  8  +  10

Ejercicio 6

ejercicio-6

F = (ln(10)+1)/1.7 + (ln(100)+2)/1.9... El argumento del Log10, está multiplicando. X10, X10,..utilice acumulador multiplicador.

Ver código

Public Function LogarithmSerie(n As Integer, initialValue As Double, razon As Double, arg As Double, sumTotal As Boolean) As String
    Dim result As String = ""
    Dim count As Double
    Dim index As Integer
    Dim t, f, total As Double
    count = arg
    t = initialValue
    For index = 1 To n
        If sumTotal Then
            f = (Math.Log10(count) + index) / t
            total += f
            result = Str(total)
        Else
            If index.Equals(n) Then
                result = result + "(ln(" + Str(count) + ")+" + Str(index) + ")/" + Str(t)
            Else
                result = result + "(ln(" + Str(count) + ")+" + Str(index) + ")/" + Str(t) + "+  "
            End If
        End If
        count *= 10
        t = Math.Round(t + razon, 2)
    Next
    Return "F = " + result
End Function

# Output: LogarithmSerie(TextBox1.Text, vi, r, arg, True)
F = 13.617137472838102
# Output string: LogarithmSerie(TextBox1.Text, vi, r, arg, False)
F = (ln(10)+1)/1.7 +  (ln(100)+ 2)/ 1.9  +  (ln(1000)+3)/2.1  + (ln(10000)+4)/2.3  +  (ln(100000)+5)/2.5

Ejercicio 7

ejercicio-7

F = 100/1 + 99/2 + 97/4... el numerador Va reduciendo el termino en 1, 2, 3… mientras que el denominador incrementando en 1,2,3…, debe tener valor inicial del numerador VIN=100, y valor inicial del denominador VID=1.

Ver código

Public Function IncreaseAndDecrease(n As Integer, initialValueNumerator As Integer, initialValueDenominator As Integer, isSumTotal As Boolean) As String
    Dim result As String = ""
    Dim index As Integer
    Dim f, total As Double
    For index = 1 To n
        If isSumTotal Then
            f = (initialValueNumerator / initialValueDenominator)
            total += f
            result = Str(total)
        Else
            If index = n Then
                result = result + Str(initialValueNumerator) + "/" + Str(initialValueDenominator)
            Else
                result = result + Str(initialValueNumerator) + "/" + Str(initialValueDenominator) + " +  "
            End If
        End If
        initialValueNumerator -= index
        initialValueDenominator += index
    Next
    Return "F =" + result
End Function

# Output: IncreaseAndDecrease(TextBox1.Text, TextBox2.Text, TextBox3.Text, True)
F = 195.3603896103896
# Output string: IncreaseAndDecrease(TextBox1.Text, TextBox2.Text, TextBox3.Text, False)
F = 100/ 1 +   99/ 2 +   97/ 4 +   94/ 7 +   90/ 11

Ejercicio 8

ejercicio-8

F = 5.25/0!+0 + 5.24/1!+1 + 5.22/2!+2... Ambos elementos son series regulares y para el denominador solo debes llamar a la función factorial, claro que debes aprender hacer el algoritmo para el examen.

Ver código

Public Function Factorial(number As Double) As Double
    Dim fac As Double
    Dim index As Integer
    If number <> 0 Then
        fac = 1
        For index = Math.Abs(number) To 1 Step -1
            fac *= index
        Next
        If number < 0 Then
            fac = -fac
        End If
    Else
        fac = 1
    End If
    Return fac
End Function
Public Function RegularSerieWithFactorial(n As Integer, initialValueNum As Double, initialValueDen As Double, sumTotal As Double) As String
    Dim result As String = ""
    Dim index As Integer
    Dim t, f, total As Double
    For index = 0 To n
        If sumTotal Then
            If initialValueDen = 0 Then
                f = 0
            Else
                f = initialValueNum / (Factorial(initialValueDen) + initialValueDen)
            End If
            total += f
            result = Str(total)
        Else
            t = index + 1
            If index = n Then
                result = result + Str(Math.Round(initialValueNum, 2)) + "/(!" + Str(initialValueDen) + "+" + Str(initialValueDen) + ")"
            Else
                result = result + Str(Math.Round(initialValueNum, 2)) + "/(!" + Str(initialValueDen) + "+" + Str(initialValueDen) + ")  +  "
            End If
        End If
        initialValueNum -= (t / 100)
        initialValueDen += 1
    Next
    Return "F = " + result
End Function

# Output: RegularSerieWithFactorial(TextBox1.Text, vi, r, True)
F = 4.750333333333333
# Output string: RegularSerieWithFactorial(TextBox1.Text, vi, r, False)
F = 5.25/(!0+0) + 5.24/(!1+1) + 5.22/(!2+2) + 5.19/(!3+3) + 5.15/(!4+4) + 5.1/(!5+5)

Ejercicio 9

ejercicio-9

F = X^2/2! + X^4/4! + X^6/6!+… X, es solo una variable de entrada que se debe tomar en el término

Ver código

Public Function SumFactorial(n As Integer, x As Single, sumTotal As Boolean) As String
    Dim result As String = ""
    Dim index As Integer
    Dim formule As Double
    If n = 0 Then
        result = Str(0)
    End If
    For index = 1 To n
        If sumTotal Then
            formule = Math.Pow(x, index * 2) / Factorial(index * 2)
            result = Str(formule)
        Else
            If index = n Then
                result = result + "(" + Str(x) + "^" + Str(index * 2) + ")/" + Str(index * 2) + "!"
            Else
                result = result + "(" + Str(x) + "^" + Str(index * 2) + ")/" + Str(index * 2) + "! + "
            End If
        End If
    Next
    Return "F = " + result
End Function

# Output: SumFactorial(TextBox1.Text, TextBox2.Text, True)
F = 0.0002821869488536155
# Output string: SumFactorial(TextBox1.Text, TextBox2.Text, False)
F = (2^2)/ 2! + (2^4)/ 4! + (2^6)/ 6! + (2^8)/ 8! + (2^10)/ 10!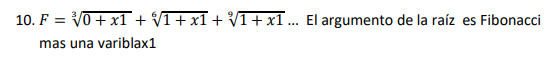

Ejercicio 10

ejercicio-10

3√(0+x1) + 6√(1+x1) + 9√(1+x1)... El argumento de la raíz es Fibonacci mas una varible x1.

Ver código

Public Function SerieProgresiveFibonacci(n As Integer, x As Double, viRoot As Integer, sumTotal As Boolean) As String
    Dim result As String = ""
    Dim index, a, b, c, root As Integer
    Dim formule, total As Double
    a = -1 : b = 1 : root = viRoot
    For index = 1 To n
        c = a + b
        If sumTotal Then
            formule = (c + x) ^ (1 / root)
            total += formule
            result = Str(total)
        Else
            If index = n Then
                result = result + Str(index * 3) + "√(" + Str(c) + "+" + Str(x) + ")"
            Else
                result = result + Str(index * 3) + "√(" + Str(c) + "+" + Str(x) + ") + "
            End If
        End If
        a = b
        b = c
        root *= 3
    Next
    Return "F = " + result
End Function

# Output: SerieProgresiveFibonacci(TextBox1.Text, TextBox2.Text, TextBox3.Text, True)
F = 5.455187736786854
# Output string: SerieProgresiveFibonacci(TextBox1.Text, TextBox2.Text, TextBox3.Text, False)
F = 3√(0+2) +  6√(1+2) +  9√(1+2) +  12√(2+2) +  15√(3+2)

Ejercicio 11

ejercicio-11

20√cos(0.2) - 19√cos(0.4) + 18√cos(0.6)... “pimponea”, o sea suma el termino y resta, suma y resta. ESTE NO ES N TERMINOS, SINO HASTA QUE LA RAIZ SEA 2 OSEA EL UTLIMO ELEMENTO SERA 2√cos(...).

Ver código

0 Then formule = -Math.Pow(Math.Cos(count), 1 / index) Else formule = Math.Pow(Math.Cos(count), 1 / index) End If total += formule result = Str(total) Else If index = 2 Then result = result + Str(index) + "√cos(" + Str(count) + ")" Else If index Mod 2 <> 0 Then result = result + Str(index) + "√cos(" + Str(count) + ") + " Else result = result + Str(index) + "√cos(" + Str(count) + ") - " End If End If End If count = Math.Round(count + razon, 2) Next Return "F = " + result End Function">

Public Shared Function Pinponear(root As Double, vi As Double, razon As Double, sumTotal As Boolean) As String
    Dim result As String = ""
    Dim index As Integer
    Dim count, total, formule As Double
    count = vi
    For index = root To 2 Step -1
        If sumTotal Then
            If index Mod 2 <> 0 Then
                formule = -Math.Pow(Math.Cos(count), 1 / index)
            Else
                formule = Math.Pow(Math.Cos(count), 1 / index)
            End If
            total += formule
            result = Str(total)
        Else
            If index = 2 Then
                result = result + Str(index) + "√cos(" + Str(count) + ")"
            Else
                If index Mod 2 <> 0 Then
                    result = result + Str(index) + "√cos(" + Str(count) + ")  + "
                Else
                    result = result + Str(index) + "√cos(" + Str(count) + ")  - "
                End If
            End If
        End If
        count = Math.Round(count + razon, 2)
    Next
    Return "F = " + result
End Function

# Output: Pinponear(TextBox1.Text, vi, r, True)
F = 5.455187736786854
# Output string: Pinponear(TextBox1.Text, vi, r, False)
F = 3√(0+2) +  6√(1+2) +  9√(1+2) +  12√(2+2) +  15√(3+2)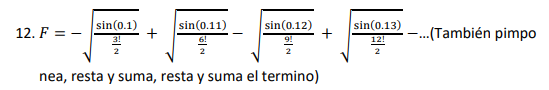

Ejercicio 12

ejercicio-12

√(sin(0.1)/(3!/2)) + √(sin(0.11)/(3!/2))... También pimponea, resta y suma, resta y suma el termino.

Ver código

Public Function ProgresiveSeriePinponear(n As Integer, initValue As Double, r As Double, arg As Double, sumTotal As Boolean)
    Dim result As String = ""
    Dim index As Integer
    Dim total, formule, count As Double
    count = initValue
    For index = 1 To n
        If sumTotal Then
            formule = Math.Sqrt(Math.Sin(arg) / (Factorial(count) / 2))
            total = -total + formule
            result = Str(total)
        Else
            If index Mod 2 = 0 Then
                result = result + "+ √sin(" + Str(arg) + ")/(" + Str(count) + "!/2) "
            Else
                result = result + "- √sin(" + Str(arg) + ")/(" + Str(count) + "!/2) "
            End If
        End If
        arg = Math.Round(arg + r, 2)
        count += 3
    Next
    Return "F = " + result
End Function

# Output: ProgresiveSeriePinponear(TextBox1.Text, vi, r, arg, True)
F = -0.16574853902978934
# Output string: ProgresiveSeriePinponear(TextBox1.Text, vi, r, arg, False)
F = - √sin( 0.1)/( 3!/2) + √sin( 0.11)/( 6!/2) - √sin( 0.12)/( 9!/2) + √sin( 0.13)/( 12!/2)

Ejercicio 13

ejercicio-13

(π/2)/√(1000+0) + (π/1.9)/√(1001+1) + (π/1.8)/√(1003+1) El argumento de la raíz va en incremento en una progresión: Del 1ro al 2do 1; del 2do al 3ro 2; del 3ro al 4to 3; …mientras que el otro es Fibonacci.

Ver código

Public Function ProgresiveSerieFibonacci(n As Integer, initValue As Integer, sumTotal As Boolean) As String
    Dim result As String = ""
    Dim index As Integer
    Dim count, a, b, c, total, formule As Double
    count = 2 : a = -1 : b = 1
    For index = 1 To n
        c = a + b
        If sumTotal Then
            formule = (3.14159 / count) / Math.Sqrt(initValue + c)
            total += formule
            result = Str(total)
        Else
            If index = n Then
                result = result + "(π/" + Str(count) + ")/√(" + Str(initValue) + "+" + Str(c) + ")"
            Else
                result = result + "(π/" + Str(count) + ")/√(" + Str(initValue) + "+" + Str(c) + ")  +  "
            End If
        End If
        a = b
        b = c
        count = Math.Round(count - 0.1, 2)
        initValue += index
    Next
    Return "F = " + result
End Function

# Output: ProgresiveSerieFibonacci(TextBox1.Text, TextBox2.Text, True)
F = 0.27688777750129406
# Output string: ProgresiveSerieFibonacci(TextBox1.Text, TextBox2.Text, False)
F = (π/ 2)/√( 1000+ 0)  +  (π/ 1.9)/√( 1001+ 1)  +  (π/ 1.8)/√( 1003+ 1)  +  (π/ 1.7)/√( 1006+ 2)  +  (π/ 1.6)/√( 1010+ 3)

Ejercicio 14

ejercicio-14

2√x^2/100 + 4√x^4/50 + 8√x^8/25... La raíz multiplica, mientras que el denominador dentro la raíz desdobla (divide).

Ver código

Public Function SerieMultiplyAndUnfold(n As Integer, root As Double, num As Double, denom As Double, sumTotal As Boolean) As String
    Dim result As String = ""
    Dim index As Integer
    Dim total, formule As Double
    For index = 1 To n
        If sumTotal Then
            formule = Math.Pow(Math.Pow(num, root) / denom, 1 / root)
            total += formule
            result = Str(total)
        Else
            If index = n Then
                result = result + Str(root) + "√(" + Str(num) + "^" + Str(root) + "/" + Str(denom) + ")"
            Else
                result = result + Str(root) + "√(" + Str(num) + "^" + Str(root) + "/" + Str(denom) + ")  +  "
            End If
        End If
        root = Math.Round(root * 2, 2)
        denom = Math.Round(denom / 2, 2)
    Next
    Return "F = " + result
End Function

# Output: SerieMultiplyAndUnfold(TextBox1.Text, TextBox2.Text,TextBox3.Text, TextBox4.Text, True)
F = 1.9987716171427177
# Output string with params: SerieMultiplyAndUnfold(4, 2, 1, 100, False)
F = 2√( 1^ 2/ 100)  +   4√( 1^ 4/ 50)  +   8√( 1^ 8/ 25)  +   16√( 1^ 16/ 12.5)

Ejercicio 15

ejercicio-15

(2+x^(1/16)) + (4+x^(1/14))... La base va doblando. OJO , HASTA QUE EL TERMINO DONDE X ELEVE A 1/2

Ver código

= 2 Then If index = n Then result = result + "(" + Str(base) + "+" + Str(x) + "^(1/" + Str(denom) + "))" Else result = result + "(" + Str(base) + "+" + Str(x) + "^(1/" + Str(denom) + ")) + " End If End If End If base *= 2 denom -= 2 Next Return "F = " + result End Function">

Public Function SerieBaseIsDoubling(n As Integer, base As Double, x As Double, denom As Double, sumTotal As Boolean) As String
    Dim result As String = ""
    Dim index As Integer
    Dim total, formule As Double
    For index = 1 To n
        If sumTotal Then
            formule = base + Math.Pow(x, 1 / denom)
            total += formule
            result = total
        Else
            If denom >= 2 Then
                If index = n Then
                    result = result + "(" + Str(base) + "+" + Str(x) + "^(1/" + Str(denom) + "))"
                Else
                    result = result + "(" + Str(base) + "+" + Str(x) + "^(1/" + Str(denom) + "))  + "
                End If
            End If
        End If
        base *= 2
        denom -= 2
    Next
    Return "F = " + result
End Function

# Output: SerieBaseIsDoubling(TextBox1.Text, vi, r, arg, True)
F = 2056
# Output string with params: SerieBaseIsDoubling(10, 2, 1, 16, False)
F = ( 2+ 1^(1/ 16))  + ( 4+ 1^(1/ 14))  + ( 8+ 1^(1/ 12))  + ( 16+ 1^(1/ 10))  + ( 32+ 1^(1/ 8))  + ( 64+ 1^(1/ 6))  + ( 128+ 1^(1/ 4))  + ( 256+ 1^(1/ 2))

Expandir

Información adicional