Inicio | Instalación | Documentación | Tutoría | Desarrolladores
rodeo es una biblioteca rápida de Python que utiliza números probabilísticos para resolver ecuaciones diferenciales ordinarias (EDO). Es decir, la mayoría de los solucionadores de EDO (como el método de Euler) producen una aproximación determinista a la EDO en una cuadrícula de tamaño de paso.
rodeo proporciona una familia ligera y extensible de aproximaciones a un paradigma de filtrado bayesiano no lineal común a muchos solucionadores probabilísticos (Tronarp et al (2018)). Esto comienza poniendo un proceso gaussiano antes de la solución ODE y actualizándolo secuencialmente a medida que el solucionador recorre la cuadrícula. rodeo se basa en jax , lo que permite la compilación y la diferenciación automática justo a tiempo. La API de jax es casi equivalente a la de numpy .
rodeo proporciona dos herramientas principales: una para aproximar la solución ODE y la otra para la inferencia de parámetros. Para el primero proporcionamos:
solve : Implementación de un solucionador ODE probabilístico que utiliza un paradigma de filtrado bayesiano no lineal.Para este último proporcionamos los métodos de aproximación de probabilidad:
basic : Implementación de un método básico de aproximación de probabilidad (los detalles se pueden encontrar en Wu y Lysy (2023)).fenrir : Implementación de Fenrir (Tronarp et al (2022)).marginal_mcmc : Implementación MCMC del método de Chkrebtii (Chkrebtii et al (2016)).dalton : Implementación de nuestra aproximación de probabilidad de EDO adaptativa a datos (Wu y Lysy (2023)).Se pueden encontrar ejemplos detallados de su uso en la sección Documentación. Tenga en cuenta que esta es la versión de rodeo exclusiva para jax . Para las versiones heredadas que utilizan otros backends, consulte aquí.
Descargue el repositorio de GitHub y luego instálelo con el script setup.cfg :
git clone https://github.com/mlysy/rodeo.git
cd rodeo
pip install . Primero vaya a readthedocs para ver la documentación renderizada de los siguientes ejemplos.
Un tutorial de inicio rápido sobre cómo resolver un problema ODE simple.
Un ejemplo para resolver una EDO de orden superior.
Un ejemplo para resolver una EDO caótica difícil.
Un ejemplo de un problema de inferencia de parámetros donde utilizamos la aproximación de Laplace.
En este tutorial, mostramos cómo resolver una EDO con nuestro solucionador probabilístico y cómo realizar la inferencia de parámetros. Primero ilustraremos la configuración para resolver la ODE. Con ese fin, consideremos el siguiente ejemplo de EDO de primer orden (modelo de FitzHugh-Nagumo ),
donde la solución
Siguiendo la notación de (Wu y Lysy (2023)), tenemos
para
import jax
import jax . numpy as jnp
import rodeo
def fitz_fun ( X , t , ** params ):
"FitzHugh-Nagumo ODE in rodeo format."
a , b , c = params [ "theta" ]
V , R = X [:, 0 ]
return jnp . array (
[[ c * ( V - V * V * V / 3 + R )],
[ - 1 / c * ( V - a + b * R )]]
)
def fitz_init ( x0 , theta ):
"FitzHugh-Nagumo initial values in rodeo format."
x0 = x0 [:, None ]
return jnp . hstack ([
x0 ,
fitz_fun ( X = x0 , t = 0. , theta = theta ),
jnp . zeros_like ( x0 )
])
W = jnp . array ([[[ 0. , 1. , 0. ]], [[ 0. , 1. , 0. ]]]) # LHS matrix of ODE
x0 = jnp . array ([ - 1. , 1. ]) # initial value for the ODE-IVP
theta = jnp . array ([ .2 , .2 , 3 ]) # ODE parameters
X0 = fitz_init ( x0 , theta ) # initial value in rodeo format
# Time interval on which a solution is sought.
t_min = 0.
t_max = 40.
# --- Define the prior process -------------------------------------------
n_vars = 2 # number of variables in the ODE
n_deriv = 3 # max number of derivatives
sigma = jnp . array ([ .1 ] * n_vars ) # IBM process scale factor
# --- data simulation ------------------------------------------------------
n_steps = 800 # number of evaluations steps
dt = ( t_max - t_min ) / n_steps # step size
# generate the Kalman parameters corresponding to the prior
prior_Q , prior_R = rodeo . prior . ibm_init (
dt = dt_sim ,
n_deriv = n_deriv ,
sigma = sigma
)
# Produce a Pseudo-RNG key
key = jax . random . PRNGKey ( 0 )
Xt , _ = rodeo . solve_mv (
key = key ,
# define ode
ode_fun = fitz_fun ,
ode_weight = W ,
ode_init = X0 ,
t_min = t_min ,
t_max = t_max ,
theta = theta , # ODE parameters added here
# solver parameters
n_steps = n_steps ,
interrogate = rodeo . interrogate . interrogate_kramer ,
prior_weight = prior_Q ,
prior_var = prior_R
) Comparamos la solución del solucionador con la solución determinista proporcionada por odeint en la biblioteca scipy .
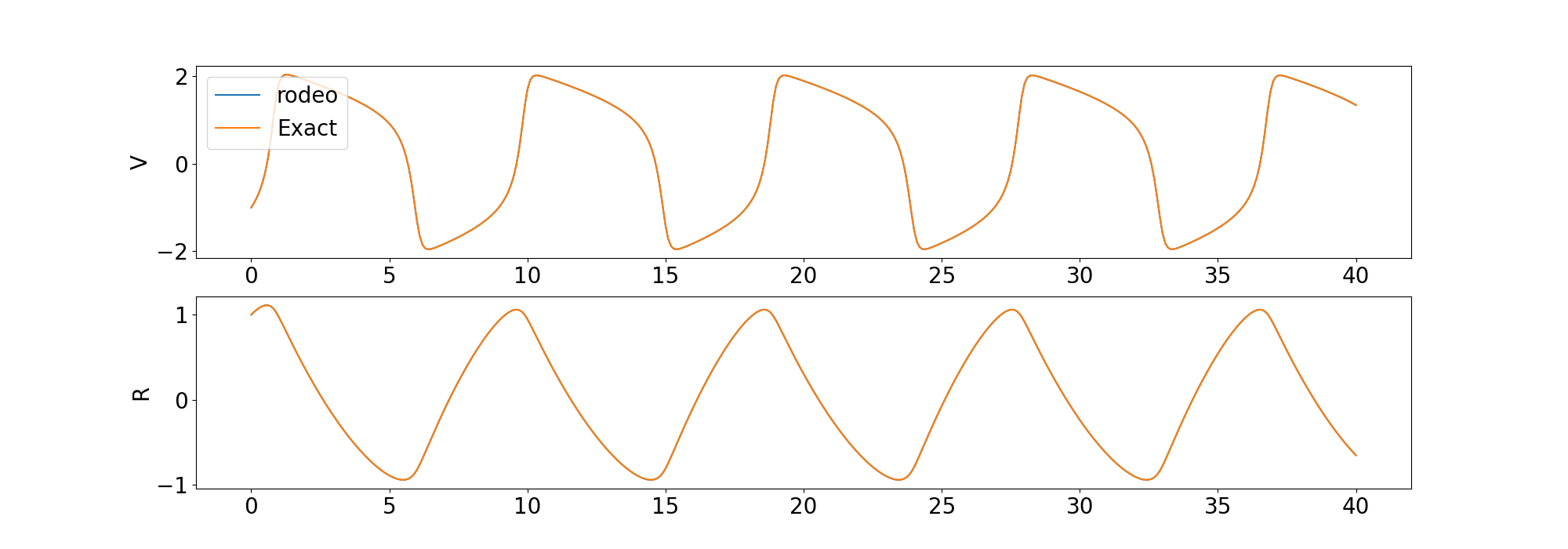
También incluimos ejemplos para resolver una EDO de orden superior y una EDO caótica.
Pasemos ahora al problema de inferencia de parámetros. rodeo contiene varios métodos de aproximación de probabilidad que se resumen en la sección Descripción. Aquí utilizaremos el método basic de aproximación de verosimilitud. Supongamos que las observaciones se simulan mediante el modelo.
dónde basic para
def fitz_logprior ( upars ):
"Logprior on unconstrained model parameters."
n_theta = 5 # number of ODE + IV parameters
lpi = jax . scipy . stats . norm . logpdf (
x = upars [: n_theta ],
loc = 0. ,
scale = 10.
)
return jnp . sum ( lpi )
def fitz_loglik ( obs_data , ode_data , ** params ):
"""
Loglikelihood for measurement model.
Args:
obs_data (ndarray(n_obs, n_vars)): Observations data.
ode_data (ndarray(n_obs, n_vars, n_deriv)): ODE solution.
"""
ll = jax . scipy . stats . norm . logpdf (
x = obs_data ,
loc = ode_data [:, :, 0 ],
scale = 0.005
)
return jnp . sum ( ll )
def constrain_pars ( upars , dt ):
"""
Convert unconstrained optimization parameters into rodeo inputs.
Args:
upars : Parameters vector on unconstrainted scale.
dt : Discretization grid size.
Returns:
tuple with elements:
- theta : ODE parameters.
- X0 : Initial values in rodeo format.
- Q, R : Prior matrices.
"""
theta = jnp . exp ( upars [: 3 ])
x0 = upars [ 3 : 5 ]
X0 = fitz_init ( x0 , theta )
sigma = upars [ 5 :]
Q , R = rodeo . prior . ibm_init (
dt = dt ,
n_deriv = n_deriv ,
sigma = sigma
)
return theta , X0 , Q , R
def neglogpost_basic ( upars ):
"Negative logposterior for basic approximation."
# solve ODE
theta , X0 , prior_Q , prior_R = constrain_pars ( upars , dt_sim )
# basic loglikelihood
ll = rodeo . inference . basic (
key = key ,
# ode specification
ode_fun = fitz_fun ,
ode_weight = W ,
ode_init = X0 ,
t_min = t_min ,
t_max = t_max ,
theta = theta ,
# solver parameters
n_steps = n_steps ,
interrogate = rodeo . interrogate . interrogate_kramer ,
prior_weight = prior_Q ,
prior_var = prior_R ,
# observations
obs_data = obs_data ,
obs_times = obs_times ,
obs_loglik = fitz_loglik
)
return - ( ll + fitz_logprior ( upars )) Este es un ejemplo básico para demostrar el uso. Sugerimos aproximaciones de probabilidad más sofisticadas que propagan la incertidumbre de la solución a la aproximación de probabilidad, como fenrir , marginal_mcmc y dalton . Consulte el tutorial de inferencia de parámetros para obtener más detalles.
A continuación se muestran algunos resultados producidos por varias aproximaciones de probabilidad encontradas en rodeo de /examples/ :
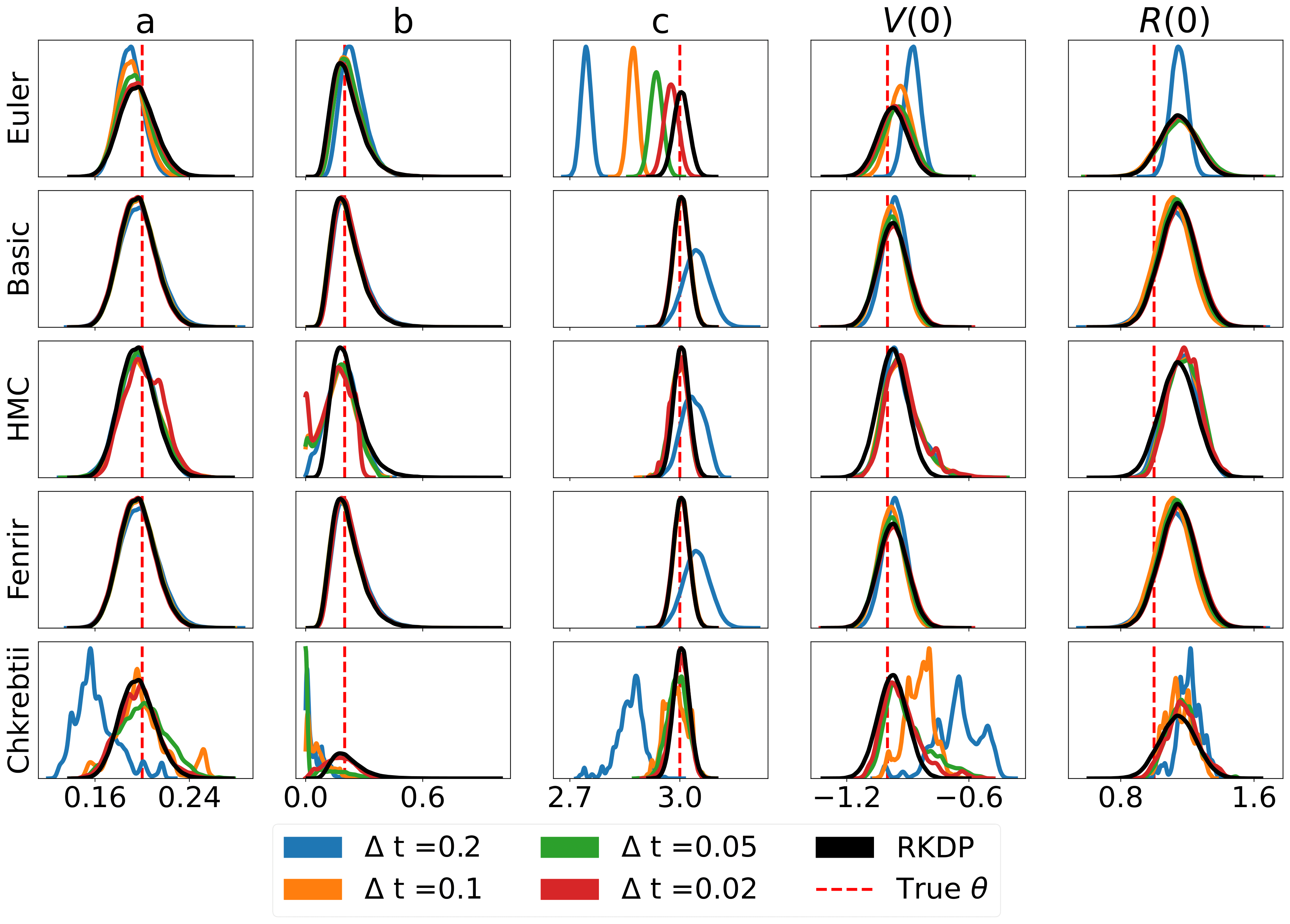
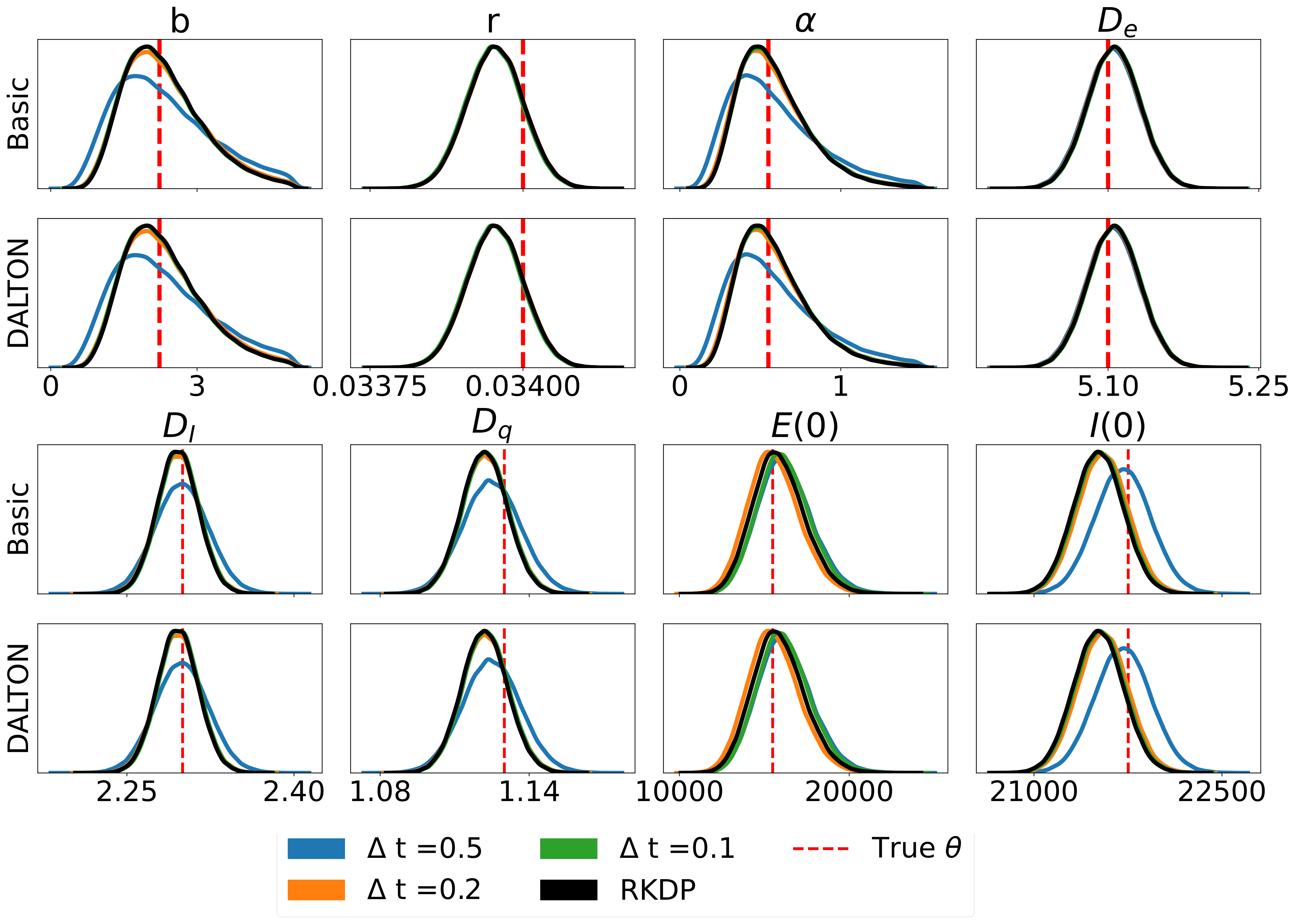
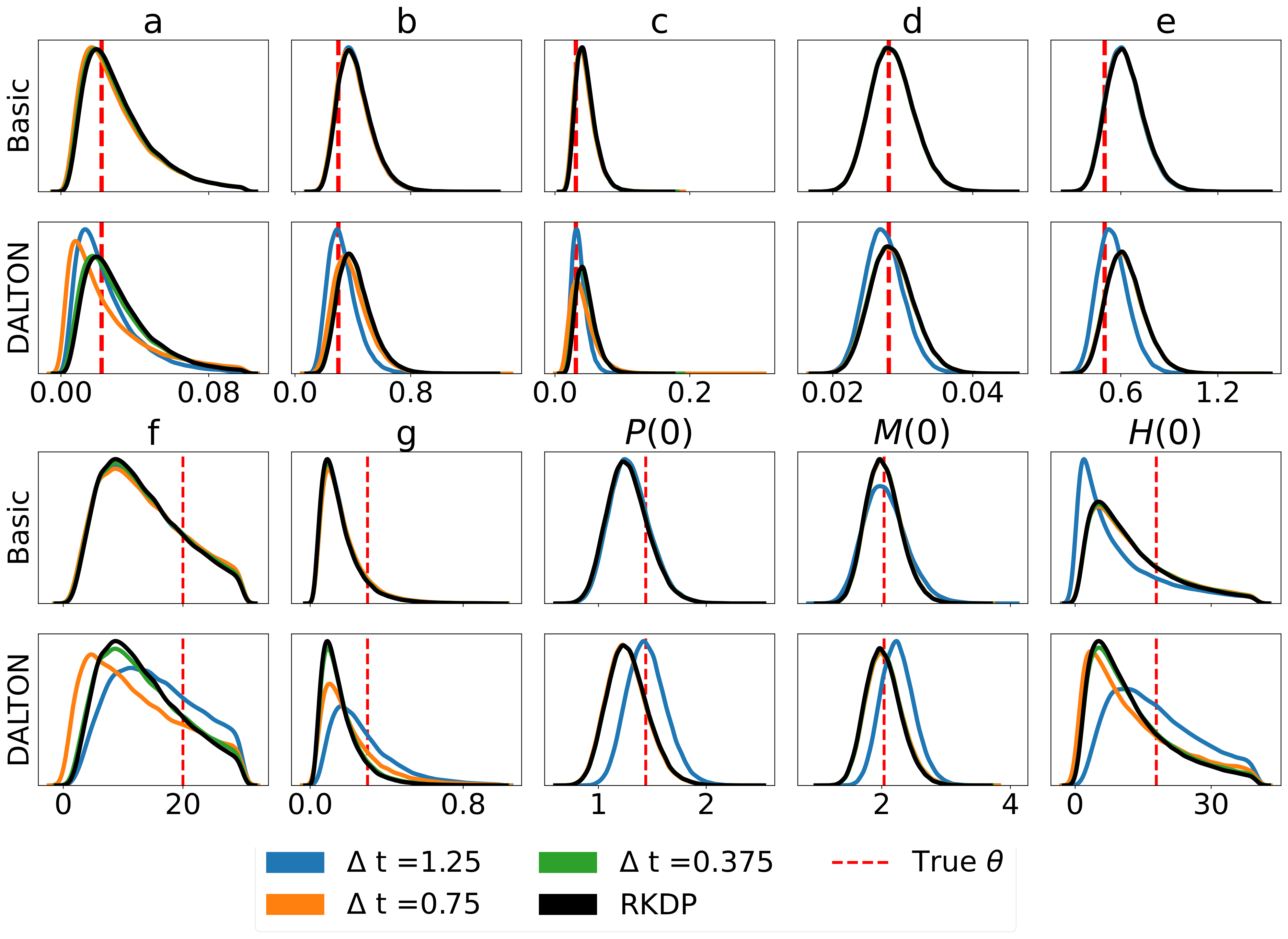
Las pruebas unitarias se pueden ejecutar mediante los siguientes comandos:
cd tests
python -m unittest discover -v O instale tox y luego, desde rodeo ingrese la línea de comando: tox .
La documentación HTML se puede compilar desde la carpeta raíz:
pip install .[docs]
cd docs
make html Esto creará la documentación en docs/build .