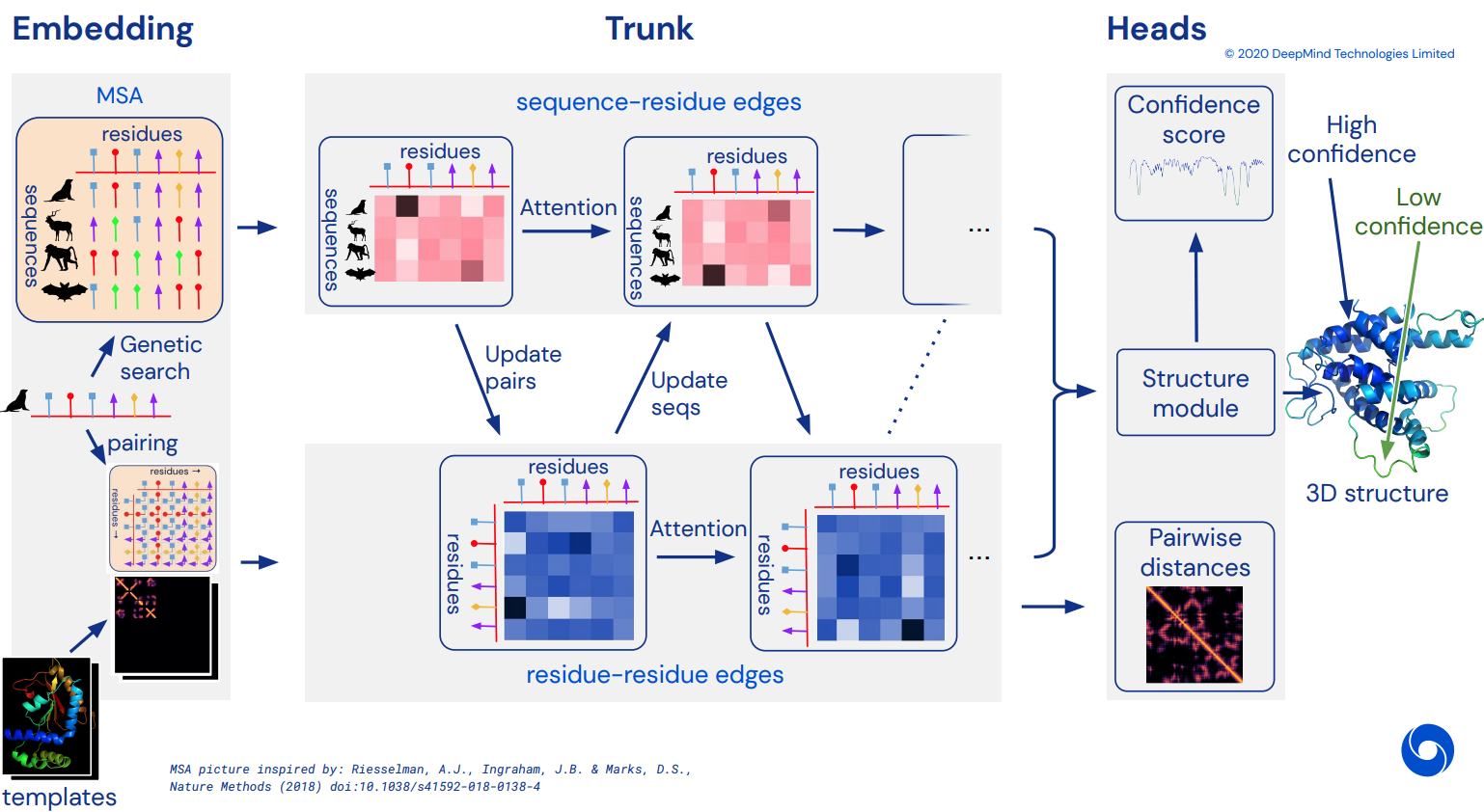
Para eventualmente convertirse en una implementación funcional no oficial de Pytorch de Alphafold2, la impresionante red de atención que resolvió CASP14. Se implementará gradualmente a medida que se publiquen más detalles de la arquitectura.
Una vez que esto se replique, tengo la intención de plegar todas las secuencias de aminoácidos disponibles in-silico y publicarlas como un torrente académico para promover la ciencia. Si está interesado en los esfuerzos de replicación, visite #alphafold en este canal de Discord.
Actualización: ¡Deepmind ha abierto el código oficial en Jax, junto con los pesos! Este repositorio ahora estará orientado a una traducción directa de pytorch con algunas mejoras en la codificación posicional.
Vídeo de ArxivInsights
$ pip install alphafold2-pytorchlhatsk ha informado que entrenó un tronco modificado de este repositorio, utilizando la misma configuración que trRosetta, con resultados competitivos.
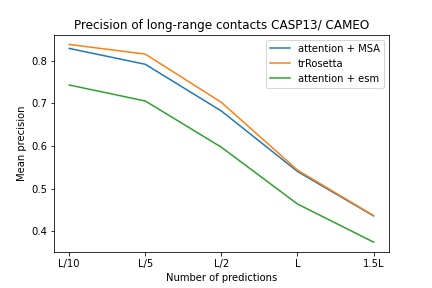
blue used the the trRosetta input (MSA -> potts -> axial attention), green used the ESM embedding (only sequence) -> tiling -> axial attention - lhatsk
Predecir distograma, como Alphafold-1, pero con atención.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
reversible = False # set this to True for fully reversible self / cross attention for the trunk
). cuda ()
seq = torch . randint ( 0 , 21 , ( 1 , 128 )). cuda () # AA length of 128
msa = torch . randint ( 0 , 21 , ( 1 , 5 , 120 )). cuda () # MSA doesn't have to be the same length as primary sequence
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
distogram = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) # (1, 128, 128, 37) También puedes activar la predicción de los ángulos, pasando predict_angles = True en init. El siguiente ejemplo sería equivalente a trRosetta pero con atención propia/cruzada.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
predict_angles = True # set this to True
). cuda ()
seq = torch . randint ( 0 , 21 , ( 1 , 128 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 1 , 5 , 120 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
distogram , theta , phi , omega = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
)
# distogram - (1, 128, 128, 37),
# theta - (1, 128, 128, 25),
# phi - (1, 128, 128, 13),
# omega - (1, 128, 128, 25) El artículo reciente de Fabian sugiere que introducir iterativamente las coordenadas en el Transformador SE3, con peso compartido, puede funcionar. He decidido ejecutar en base a esta idea, aunque todavía está en el aire cómo funciona realmente.
También puede utilizar E(n)-Transformer o EGNN para refinamiento estructural.
Actualización: el laboratorio de Baker ha demostrado que una arquitectura de extremo a extremo desde secuencias e incrustaciones de MSA hasta transformadores SE3 puede mejorar trRosetta y cerrar la brecha con Alphafold2. Usaremos el Graph Transformer, que actúa sobre las incrustaciones del tronco, para generar el conjunto inicial de coordenadas que se enviará a la red equivariante. (Esto lo corrobora aún más Costa et al en su trabajo que desentraña las coordenadas 3D de las incrustaciones de MSA Transformer en un artículo anterior al del laboratorio Baker)
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
predict_coords = True ,
structure_module_type = 'se3' , # use SE3 Transformer - if set to False, will use E(n)-Transformer, Victor and Max Welling's new paper
structure_module_dim = 4 , # se3 transformer dimension
structure_module_depth = 1 , # depth
structure_module_heads = 1 , # heads
structure_module_dim_head = 16 , # dimension of heads
structure_module_refinement_iters = 2 , # number of equivariant coordinate refinement iterations
structure_num_global_nodes = 1 # number of global nodes for the structure module, only works with SE3 transformer
). cuda ()
seq = torch . randint ( 0 , 21 , ( 2 , 64 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 2 , 5 , 60 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
coords = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) # (2, 64 * 3, 3) <-- 3 atoms per residue La suposición subyacente es que el tronco funciona en el nivel de residuos y luego constituye el nivel atómico para el módulo de estructura, ya sean transformadores SE3, transformadores E(n) o EGNN que realizan el refinamiento. Esta biblioteca tiene como valor predeterminado los 3 átomos de la columna vertebral (C, Ca, N), pero puede configurarla para incluir cualquier otro átomo que desee, incluidos Cb y las cadenas laterales.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
predict_coords = True ,
atoms = 'backbone-with-cbeta'
). cuda ()
seq = torch . randint ( 0 , 21 , ( 2 , 64 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 2 , 5 , 60 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
coords = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) # (2, 64 * 4, 3) <-- 4 atoms per residue (C, Ca, N, Cb) Las opciones válidas para atoms incluyen:
backbone - 3 átomos de la columna vertebral (C, Ca, N) [predeterminado]backbone-with-cbeta - 3 átomos de columna vertebral y C betabackbone-with-oxygen : 3 átomos de columna vertebral y oxígeno del carboxilobackbone-with-cbeta-and-oxygen - 3 átomos de columna vertebral con C beta y oxígenoall : columna vertebral y todos los demás átomos de la cadena lateralTambién puedes pasar un tensor de forma (14), definiendo qué átomos te gustaría incluir.
ex.
atoms = torch . tensor ([ 1 , 1 , 1 , 1 , 1 , 1 , 0 , 1 , 0 , 0 , 0 , 0 , 0 , 1 ])Este repositorio le ofrece un complemento sencillo de la red con incorporaciones previamente entrenadas de Facebook AI. Contiene envoltorios para ESM, MSA Transformers o Protein Transformer previamente entrenados.
Hay algunos requisitos previos. Deberá asegurarse de tener instalada la biblioteca apex de Nvidia, ya que los transformadores previamente entrenados utilizan algunas operaciones fusionadas.
O puede intentar ejecutar el siguiente script
git clone https://github.com/NVIDIA/apex
cd apex
pip install -v --disable-pip-version-check --no-cache-dir --global-option= " --cpp_ext " --global-option= " --cuda_ext " ./ A continuación, simplemente tendrá que importar y empaquetar su instancia Alphafold2 con ESMEmbedWrapper , MSAEmbedWrapper o ProtTranEmbedWrapper y este se encargará de incrustar tanto la secuencia como las alineaciones de secuencias múltiples por usted (y proyectarlas a las dimensiones especificadas en su modelo). No es necesario cambiar nada excepto agregar el contenedor.
import torch
from alphafold2_pytorch import Alphafold2
from alphafold2_pytorch . embeds import MSAEmbedWrapper
alphafold2 = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64
)
model = MSAEmbedWrapper (
alphafold2 = alphafold2
). cuda ()
seq = torch . randint ( 0 , 21 , ( 2 , 16 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa = torch . randint ( 0 , 21 , ( 2 , 5 , 16 )). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
distogram = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) De forma predeterminada, incluso si el contenedor proporciona al troncal la secuencia y las incrustaciones de MSA, se sumarían con las incrustaciones de tokens habituales. Si desea entrenar Alphafold2 sin incrustaciones de tokens (confíe solo en incrustaciones previamente entrenadas), deberá configurar disable_token_embed en True en el inicio Alphafold2 .
alphafold2 = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
disable_token_embed = True
) Un artículo de Jinbo Xu sugiere que no es necesario agrupar las distancias y, en cambio, se puede predecir la media y la desviación estándar directamente. Puede usar esto activando una bandera predict_real_value_distances , en cuyo caso, la predicción de distancia devuelta tendrá una dimensión de 2 para la media y la desviación estándar respectivamente.
Si predict_coords también está activado, entonces el MDS aceptará las predicciones de media y desviación estándar directamente sin tener que calcularlas a partir de los contenedores de distogramas.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
predict_coords = True ,
predict_real_value_distances = True , # set this to True
structure_module_type = 'se3' ,
structure_module_dim = 4 ,
structure_module_depth = 1 ,
structure_module_heads = 1 ,
structure_module_dim_head = 16 ,
structure_module_refinement_iters = 2
). cuda ()
seq = torch . randint ( 0 , 21 , ( 2 , 64 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 2 , 5 , 60 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
coords = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) # (2, 64 * 3, 3) <-- 3 atoms per residue Puede agregar bloques convolucionales, tanto para la secuencia primaria como para el MSA, simplemente configurando un argumento de palabra clave adicional use_conv = True
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
use_conv = True # set this to True
). cuda ()
seq = torch . randint ( 0 , 21 , ( 1 , 128 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 1 , 5 , 120 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
distogram = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) # (1, 128, 128, 37)Los núcleos convolucionales siguen el ejemplo de este artículo, combinando núcleos 1d y 2d en un bloque tipo resnet. Puede personalizar completamente los kernels como tales.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
use_conv = True , # set this to True
conv_seq_kernels = (( 9 , 1 ), ( 1 , 9 ), ( 3 , 3 )), # kernels for N x N primary sequence
conv_msa_kernels = (( 1 , 9 ), ( 3 , 3 )), # kernels for {num MSAs} x N MSAs
). cuda ()
seq = torch . randint ( 0 , 21 , ( 1 , 128 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 1 , 5 , 120 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
distogram = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) # (1, 128, 128, 37) También puedes dilatar el ciclo con un argumento de palabra clave adicional. La dilatación predeterminada es 1 para todas las capas.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
use_conv = True , # set this to True
dilations = ( 1 , 3 , 5 ) # cycle between dilations of 1, 3, 5
). cuda ()
seq = torch . randint ( 0 , 21 , ( 1 , 128 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 1 , 5 , 120 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
distogram = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) # (1, 128, 128, 37) Finalmente, en lugar de seguir el patrón de convoluciones, autoatención y atención cruzada por repetición en profundidad, puede personalizar cualquier orden que desee con la palabra clave custom_block_types
ex. Una red en la que primero se hacen predominantemente convoluciones, seguidas de bloques de autoatención + atención cruzada.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
heads = 8 ,
dim_head = 64 ,
custom_block_types = (
* (( 'conv' ,) * 6 ),
* (( 'self' , 'cross' ) * 6 )
)
). cuda ()
seq = torch . randint ( 0 , 21 , ( 1 , 128 )). cuda ()
msa = torch . randint ( 0 , 21 , ( 1 , 5 , 120 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
distogram = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask
) # (1, 128, 128, 37) Puedes entrenar con Sparse Attention de Microsoft Deepspeed, pero tendrás que soportar el proceso de instalación. Son dos pasos.
Primero, necesitas instalar Deepspeed con Sparse Attention
$ sh install_deepspeed.sh A continuación, debe instalar el paquete pip triton
$ pip install tritonSi ambas cosas anteriores tuvieron éxito, ¡ahora puedes entrenar con Sparse Attention!
Lamentablemente, la escasa atención sólo se apoya en la atención personal y no en la atención cruzada. Presentaré una solución diferente para hacer que la atención cruzada sea eficaz.
model = Alphafold2 (
dim = 256 ,
depth = 12 ,
heads = 8 ,
dim_head = 64 ,
max_seq_len = 2048 , # the maximum sequence length, this is required for sparse attention. the input cannot exceed what is set here
sparse_self_attn = ( True , False ) * 6 # interleave sparse and full attention for all 12 layers
). cuda ()También agregué una de las mejores variantes de atención lineal, con la esperanza de disminuir la carga de la atención cruzada. Personalmente, no he encontrado que Performer funcione tan bien, pero como en el documento informaron algunos números correctos para los puntos de referencia de proteínas, pensé en incluirlo y permitir que otros experimenten.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
cross_attn_linear = True # simply set this to True to use Performer for all cross attention
). cuda ()También puede especificar las capas exactas en las que desea utilizar atención lineal pasando una tupla de la misma longitud que la profundidad.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 6 ,
heads = 8 ,
dim_head = 64 ,
cross_attn_linear = ( True , False ) * 3 # interleave linear and full attention
). cuda ()Este artículo sugiere que si tiene consultas o contextos que tienen ejes definidos (por ejemplo, una imagen), puede reducir la cantidad de atención necesaria promediando esos ejes (alto y ancho) y concatenando los axiales promediados en una secuencia. Puedes activar esto como una técnica de ahorro de memoria para la atención cruzada, específicamente para la secuencia principal.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 6 ,
heads = 8 ,
dim_head = 64 ,
cross_attn_kron_primary = True # make sure primary sequence undergoes the kronecker operator during cross attention
). cuda () También puede aplicar el mismo operador a los MSA durante la atención cruzada con la bandera cross_attn_kron_msa , si sus MSA están alineados y tienen el mismo ancho.
Hacer
Para ahorrar memoria para atención cruzada, puede establecer una relación de compresión para la clave/valores, siguiendo el esquema establecido en este documento. Generalmente es aceptable una relación de compresión de 2 a 4.
model = Alphafold2 (
dim = 256 ,
depth = 12 ,
heads = 8 ,
dim_head = 64 ,
cross_attn_compress_ratio = 3
). cuda ()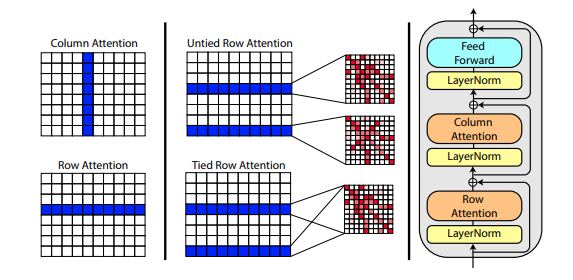
Un nuevo artículo de Roshan Rao propone utilizar la atención axial para el entrenamiento previo en MSA. Dados los buenos resultados, este repositorio utilizará el mismo esquema en el tronco, específicamente para la autoatención de MSA.
También puede vincular las atenciones de fila del MSA con la configuración msa_tie_row_attn = True en la inicialización de Alphafold2 . Sin embargo, para poder utilizar esto, debe asegurarse de que, si tiene un número impar de MSA por secuencia primaria, la máscara de MSA esté configurada correctamente en False para las filas que no están en uso.
model = Alphafold2 (
dim = 256 ,
depth = 2 ,
heads = 8 ,
dim_head = 64 ,
msa_tie_row_attn = True # just set this to true
)El procesamiento de plantillas también se realiza en gran medida con atención axial, con atención cruzada a lo largo del número de dimensiones de plantillas. Esto sigue en gran medida el mismo esquema que en el reciente enfoque de atención total para la clasificación de videos, como se muestra aquí.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 5 ,
heads = 8 ,
dim_head = 64 ,
reversible = True ,
sparse_self_attn = False ,
max_seq_len = 256 ,
cross_attn_compress_ratio = 3
). cuda ()
seq = torch . randint ( 0 , 21 , ( 1 , 16 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa = torch . randint ( 0 , 21 , ( 1 , 10 , 16 )). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
templates_seq = torch . randint ( 0 , 21 , ( 1 , 2 , 16 )). cuda ()
templates_coors = torch . randint ( 0 , 37 , ( 1 , 2 , 16 , 3 )). cuda ()
templates_mask = torch . ones_like ( templates_seq ). bool (). cuda ()
distogram = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask ,
templates_seq = templates_seq ,
templates_coors = templates_coors ,
templates_mask = templates_mask
)Si la información de la cadena lateral también está presente, en forma de vector unitario entre las coordenadas C y C-alfa de cada residuo, también puede pasarla de la siguiente manera.
import torch
from alphafold2_pytorch import Alphafold2
model = Alphafold2 (
dim = 256 ,
depth = 5 ,
heads = 8 ,
dim_head = 64 ,
reversible = True ,
sparse_self_attn = False ,
max_seq_len = 256 ,
cross_attn_compress_ratio = 3
). cuda ()
seq = torch . randint ( 0 , 21 , ( 1 , 16 )). cuda ()
mask = torch . ones_like ( seq ). bool (). cuda ()
msa = torch . randint ( 0 , 21 , ( 1 , 10 , 16 )). cuda ()
msa_mask = torch . ones_like ( msa ). bool (). cuda ()
templates_seq = torch . randint ( 0 , 21 , ( 1 , 2 , 16 )). cuda ()
templates_coors = torch . randn ( 1 , 2 , 16 , 3 ). cuda ()
templates_mask = torch . ones_like ( templates_seq ). bool (). cuda ()
templates_sidechains = torch . randn ( 1 , 2 , 16 , 3 ). cuda () # unit vectors of difference of C and C-alpha coordinates
distogram = model (
seq ,
msa ,
mask = mask ,
msa_mask = msa_mask ,
templates_seq = templates_seq ,
templates_mask = templates_mask ,
templates_coors = templates_coors ,
templates_sidechains = templates_sidechains
)He preparado una reimplementación de SE3 Transformer, como lo explica Fabian Fuchs en una entrada de blog especulativa.
Además, un nuevo artículo de Victor y Welling utiliza características invariantes para la equivarianza E(n), alcanzando SOTA y superando a SE3 Transformer en varios puntos de referencia, a la vez que es mucho más rápido. Tomé las ideas principales de este documento y lo modifiqué para convertirlo en un transformador (agregué atención tanto a las características como a las actualizaciones de coordenadas).
Las tres redes equivariantes anteriores se han integrado y están disponibles para su uso en el repositorio para el refinamiento de coordenadas atómicas simplemente configurando un hiperparámetro structure_module_type .
se3 SE3 Transformador
egnn egnn
en E(n)-Transformador
De interés para los lectores, cada uno de los tres marcos también ha sido validado por investigadores en problemas relacionados.
$ python setup.py test Esta biblioteca utilizará el increíble trabajo de Jonathan King en este repositorio. ¡Gracias Jonatán!
También tenemos los datos de MSA, todos con un valor de ~3,5 TB, descargados y alojados por Archivist, propietario del proyecto The-Eye. (También albergan los datos y modelos de Eleuther AI) Considere hacer una donación si los encuentra útiles.
$ curl -s https://the-eye.eu/eleuther_staging/globus_stuffs/tree.txthttps://xukui.cn/alphafold2.html
https://moalquraishi.wordpress.com/2020/12/08/alphafold2-casp14-it-feels-like-one-child-has-left-home/

https://www.biorxiv.org/content/10.1101/2020.12.10.419994v1.full.pdf
https://pubmed.ncbi.nlm.nih.gov/33637700/
Presentación tFold, de los laboratorios Tencent AI
cd downloads_folder > pip install pyrosetta_wheel_filename.whlOpenMM Ámbar
@misc { unpublished2021alphafold2 ,
title = { Alphafold2 } ,
author = { John Jumper } ,
year = { 2020 } ,
archivePrefix = { arXiv } ,
primaryClass = { q-bio.BM }
} @article { Rao2021.02.12.430858 ,
author = { Rao, Roshan and Liu, Jason and Verkuil, Robert and Meier, Joshua and Canny, John F. and Abbeel, Pieter and Sercu, Tom and Rives, Alexander } ,
title = { MSA Transformer } ,
year = { 2021 } ,
publisher = { Cold Spring Harbor Laboratory } ,
URL = { https://www.biorxiv.org/content/early/2021/02/13/2021.02.12.430858 } ,
journal = { bioRxiv }
} @article { Rives622803 ,
author = { Rives, Alexander and Goyal, Siddharth and Meier, Joshua and Guo, Demi and Ott, Myle and Zitnick, C. Lawrence and Ma, Jerry and Fergus, Rob } ,
title = { Biological Structure and Function Emerge from Scaling Unsupervised Learning to 250 Million Protein Sequences } ,
year = { 2019 } ,
doi = { 10.1101/622803 } ,
publisher = { Cold Spring Harbor Laboratory } ,
journal = { bioRxiv }
} @article { Elnaggar2020.07.12.199554 ,
author = { Elnaggar, Ahmed and Heinzinger, Michael and Dallago, Christian and Rehawi, Ghalia and Wang, Yu and Jones, Llion and Gibbs, Tom and Feher, Tamas and Angerer, Christoph and Steinegger, Martin and BHOWMIK, DEBSINDHU and Rost, Burkhard } ,
title = { ProtTrans: Towards Cracking the Language of Life{textquoteright}s Code Through Self-Supervised Deep Learning and High Performance Computing } ,
elocation-id = { 2020.07.12.199554 } ,
year = { 2021 } ,
doi = { 10.1101/2020.07.12.199554 } ,
publisher = { Cold Spring Harbor Laboratory } ,
URL = { https://www.biorxiv.org/content/early/2021/05/04/2020.07.12.199554 } ,
eprint = { https://www.biorxiv.org/content/early/2021/05/04/2020.07.12.199554.full.pdf } ,
journal = { bioRxiv }
} @misc { king2020sidechainnet ,
title = { SidechainNet: An All-Atom Protein Structure Dataset for Machine Learning } ,
author = { Jonathan E. King and David Ryan Koes } ,
year = { 2020 } ,
eprint = { 2010.08162 } ,
archivePrefix = { arXiv } ,
primaryClass = { q-bio.BM }
} @misc { alquraishi2019proteinnet ,
title = { ProteinNet: a standardized data set for machine learning of protein structure } ,
author = { Mohammed AlQuraishi } ,
year = { 2019 } ,
eprint = { 1902.00249 } ,
archivePrefix = { arXiv } ,
primaryClass = { q-bio.BM }
} @misc { gomez2017reversible ,
title = { The Reversible Residual Network: Backpropagation Without Storing Activations } ,
author = { Aidan N. Gomez and Mengye Ren and Raquel Urtasun and Roger B. Grosse } ,
year = { 2017 } ,
eprint = { 1707.04585 } ,
archivePrefix = { arXiv } ,
primaryClass = { cs.CV }
} @misc { fuchs2021iterative ,
title = { Iterative SE(3)-Transformers } ,
author = { Fabian B. Fuchs and Edward Wagstaff and Justas Dauparas and Ingmar Posner } ,
year = { 2021 } ,
eprint = { 2102.13419 } ,
archivePrefix = { arXiv } ,
primaryClass = { cs.LG }
} @misc { satorras2021en ,
title = { E(n) Equivariant Graph Neural Networks } ,
author = { Victor Garcia Satorras and Emiel Hoogeboom and Max Welling } ,
year = { 2021 } ,
eprint = { 2102.09844 } ,
archivePrefix = { arXiv } ,
primaryClass = { cs.LG }
} @misc { su2021roformer ,
title = { RoFormer: Enhanced Transformer with Rotary Position Embedding } ,
author = { Jianlin Su and Yu Lu and Shengfeng Pan and Bo Wen and Yunfeng Liu } ,
year = { 2021 } ,
eprint = { 2104.09864 } ,
archivePrefix = { arXiv } ,
primaryClass = { cs.CL }
} @article { Gao_2020 ,
title = { Kronecker Attention Networks } ,
ISBN = { 9781450379984 } ,
url = { http://dx.doi.org/10.1145/3394486.3403065 } ,
DOI = { 10.1145/3394486.3403065 } ,
journal = { Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining } ,
publisher = { ACM } ,
author = { Gao, Hongyang and Wang, Zhengyang and Ji, Shuiwang } ,
year = { 2020 } ,
month = { Jul }
} @article { Si2021.05.10.443415 ,
author = { Si, Yunda and Yan, Chengfei } ,
title = { Improved protein contact prediction using dimensional hybrid residual networks and singularity enhanced loss function } ,
elocation-id = { 2021.05.10.443415 } ,
year = { 2021 } ,
doi = { 10.1101/2021.05.10.443415 } ,
publisher = { Cold Spring Harbor Laboratory } ,
URL = { https://www.biorxiv.org/content/early/2021/05/11/2021.05.10.443415 } ,
eprint = { https://www.biorxiv.org/content/early/2021/05/11/2021.05.10.443415.full.pdf } ,
journal = { bioRxiv }
} @article { Costa2021.06.02.446809 ,
author = { Costa, Allan and Ponnapati, Manvitha and Jacobson, Joseph M. and Chatterjee, Pranam } ,
title = { Distillation of MSA Embeddings to Folded Protein Structures with Graph Transformers } ,
year = { 2021 } ,
doi = { 10.1101/2021.06.02.446809 } ,
publisher = { Cold Spring Harbor Laboratory } ,
URL = { https://www.biorxiv.org/content/early/2021/06/02/2021.06.02.446809 } ,
eprint = { https://www.biorxiv.org/content/early/2021/06/02/2021.06.02.446809.full.pdf } ,
journal = { bioRxiv }
} @article { Baek2021.06.14.448402 ,
author = { Baek, Minkyung and DiMaio, Frank and Anishchenko, Ivan and Dauparas, Justas and Ovchinnikov, Sergey and Lee, Gyu Rie and Wang, Jue and Cong, Qian and Kinch, Lisa N. and Schaeffer, R. Dustin and Mill{'a}n, Claudia and Park, Hahnbeom and Adams, Carson and Glassman, Caleb R. and DeGiovanni, Andy and Pereira, Jose H. and Rodrigues, Andria V. and van Dijk, Alberdina A. and Ebrecht, Ana C. and Opperman, Diederik J. and Sagmeister, Theo and Buhlheller, Christoph and Pavkov-Keller, Tea and Rathinaswamy, Manoj K and Dalwadi, Udit and Yip, Calvin K and Burke, John E and Garcia, K. Christopher and Grishin, Nick V. and Adams, Paul D. and Read, Randy J. and Baker, David } ,
title = { Accurate prediction of protein structures and interactions using a 3-track network } ,
year = { 2021 } ,
doi = { 10.1101/2021.06.14.448402 } ,
publisher = { Cold Spring Harbor Laboratory } ,
URL = { https://www.biorxiv.org/content/early/2021/06/15/2021.06.14.448402 } ,
eprint = { https://www.biorxiv.org/content/early/2021/06/15/2021.06.14.448402.full.pdf } ,
journal = { bioRxiv }
}