Una implementación del algoritmo Minimax AI en el juego Tic-Tac-Toe (o Noughts and Crosses). Pruébalo: tres en raya - Minimax
Para resolver juegos usando IA, introduciremos el concepto de árbol de juegos seguido de un algoritmo minimax. Los diferentes estados del juego están representados por nodos en el árbol del juego, muy similar a los problemas de planificación anteriores. La idea es ligeramente diferente. En el árbol del juego, los nodos están organizados en niveles que corresponden a los turnos de cada jugador en el juego, de modo que el nodo "raíz" del árbol (generalmente representado en la parte superior del diagrama) es la posición inicial del juego. En el tres en raya, esta sería la cuadrícula vacía sin X ni Os reproducidas todavía. Debajo de la raíz, en el segundo nivel, están los posibles estados que pueden resultar de los movimientos del primer jugador, ya sea X u O. Llamamos a estos nodos los "hijos" del nodo raíz.
Cada nodo en el segundo nivel tendría además como nodos secundarios los estados a los que se puede llegar desde él mediante los movimientos del jugador contrario. Esto continúa, nivel por nivel, hasta llegar a estados donde el juego termina. En el tres en raya, esto significa que uno de los jugadores obtiene una línea de tres y gana, o el tablero está lleno y el juego termina en empate.
Minimax es una inteligencia artificial aplicada en juegos de dos jugadores, como tres en raya, damas, ajedrez y go. Estos juegos se conocen como juegos de suma cero, porque en una representación matemática: un jugador gana (+1) y otro pierde (-1) o ambos o cualquiera no gana (0).
El algoritmo busca, de forma recursiva, la mejor jugada que lleve al jugador Max a ganar o no perder (empate). Considera el estado actual del juego y los movimientos disponibles en ese estado, luego realiza cada movimiento válido (alternando mínimo y máximo ) hasta que encuentra un estado terminal (ganar, empatar o perder).
El algoritmo fue estudiado en el libro Algorithms in a Nutshell (George Heineman; Gary Pollice; Stanley Selkow, 2009). Pseudocódigo (adaptado):
minimax(state, depth, player)
if (player = max) then
best = [null, -infinity]
else
best = [null, +infinity]
if (depth = 0 or gameover) then
score = evaluate this state for player
return [null, score]
for each valid move m for player in state s do
execute move m on s
[move, score] = minimax(s, depth - 1, -player)
undo move m on s
if (player = max) then
if score > best.score then best = [move, score]
else
if score < best.score then best = [move, score]
return best
end
Ahora veremos cada parte de este pseudocódigo con implementación en Python. La implementación de Python está disponible en este repositorio. Primero que nada, considérelo:
tablero = [ [0, 0, 0], [0, 0, 0], [0, 0, 0] ]
MÁX = +1
MÍN = -1
El MAX puede ser X u O y el MIN puede ser O o X, lo que sea. El tablero es de 3x3.
def minimax ( state , depth , player ): if player == MAX :
return [ - 1 , - 1 , - infinity ]
else :
return [ - 1 , - 1 , + infinity ]Ambos jugadores empiezan con tu peor puntuación. Si el jugador es MAX, su puntuación es -infinito. De lo contrario, si el jugador es MIN, su puntuación es +infinito. Nota: infinito es un alias de inf (del módulo matemático, en Python).
El mejor movimiento en el tablero es [-1, -1] (fila y columna) para todos.
if depth == 0 or game_over ( state ):
score = evaluate ( state )
return scoreSi la profundidad es igual a cero, entonces el tablero no tiene nuevas celdas vacías para jugar. O, si un jugador gana, el juego terminará en MAX o MIN. Entonces se devolverá la puntuación de ese estado.
Ahora veremos la parte principal de este código que contiene recursividad.
for cell in empty_cells ( state ):
x , y = cell [ 0 ], cell [ 1 ]
state [ x ][ y ] = player
score = minimax ( state , depth - 1 , - player )
state [ x ][ y ] = 0
score [ 0 ], score [ 1 ] = x , yPara cada movimiento válido (celdas vacías):
El movimiento (+1 o -1) en el tablero se deshace y se recogen la fila y la columna.
El siguiente paso es comparar la puntuación con la mejor.
if player == MAX :
if score [ 2 ] > best [ 2 ]:
best = score
else :
if score [ 2 ] < best [ 2 ]:
best = scorePara el jugador MAX, se recibirá una puntuación mayor. Para un jugador MIN, se recibirá una puntuación más baja. Y al final, se devuelve la mejor jugada. Algoritmo final:
def minimax ( state , depth , player ):
if player == MAX :
best = [ - 1 , - 1 , - infinity ]
else :
best = [ - 1 , - 1 , + infinity ]
if depth == 0 or game_over ( state ):
score = evaluate ( state )
return [ - 1 , - 1 , score ]
for cell in empty_cells ( state ):
x , y = cell [ 0 ], cell [ 1 ]
state [ x ][ y ] = player
score = minimax ( state , depth - 1 , - player )
state [ x ][ y ] = 0
score [ 0 ], score [ 1 ] = x , y
if player == MAX :
if score [ 2 ] > best [ 2 ]:
best = score
else :
if score [ 2 ] < best [ 2 ]:
best = score
return best A continuación, el mejor movimiento es el del medio porque el valor máximo está en el segundo nodo a la izquierda.
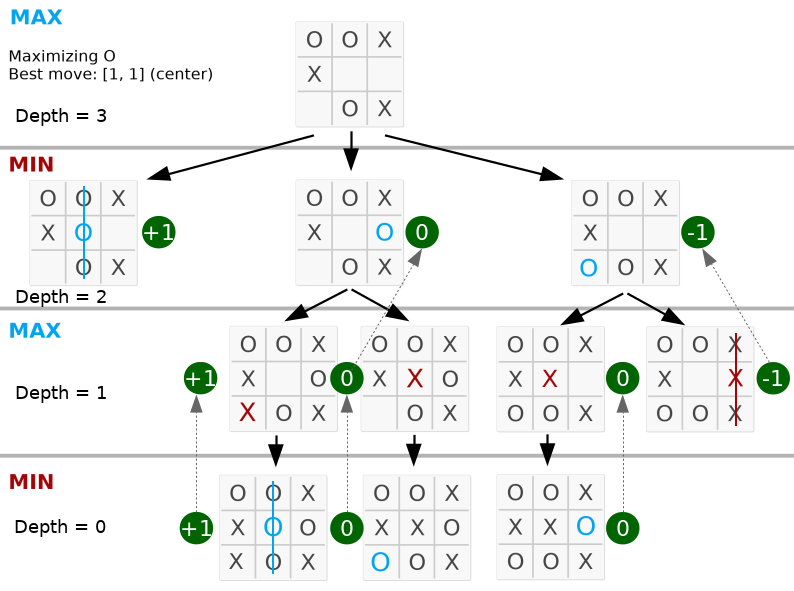
Fíjate que la profundidad es igual a los movimientos válidos en el tablero. El código completo está disponible en py_version/ .
Árbol de juego simplificado:
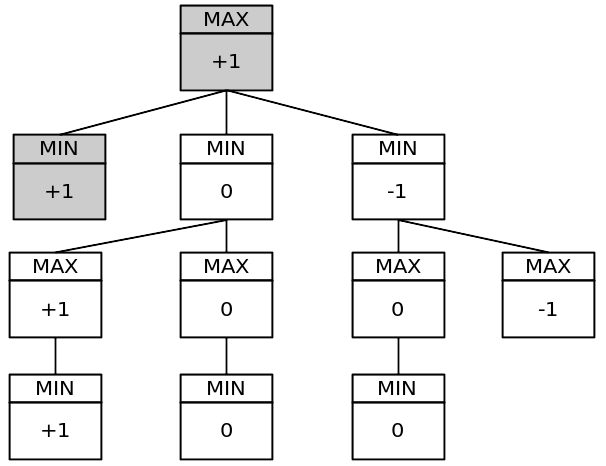
Ese árbol tiene 11 nodos. ¡El árbol de juego completo tiene 549.946 nodos! Puede probarlo colocando una variable global estática en su programa e incrementándola para cada llamada a la función minimax por turno.
En un juego más complejo, como el ajedrez, es difícil buscar en todo el árbol del juego. Sin embargo, la poda alfa-beta es un método de optimización del algoritmo minimax que nos permite ignorar algunas ramas en el árbol de búsqueda, porque corta nodos (subárboles) irrelevantes en la búsqueda. Para obtener más información, consulte: