se3 transformer pytorch

Transformador SE3 - Pytorch

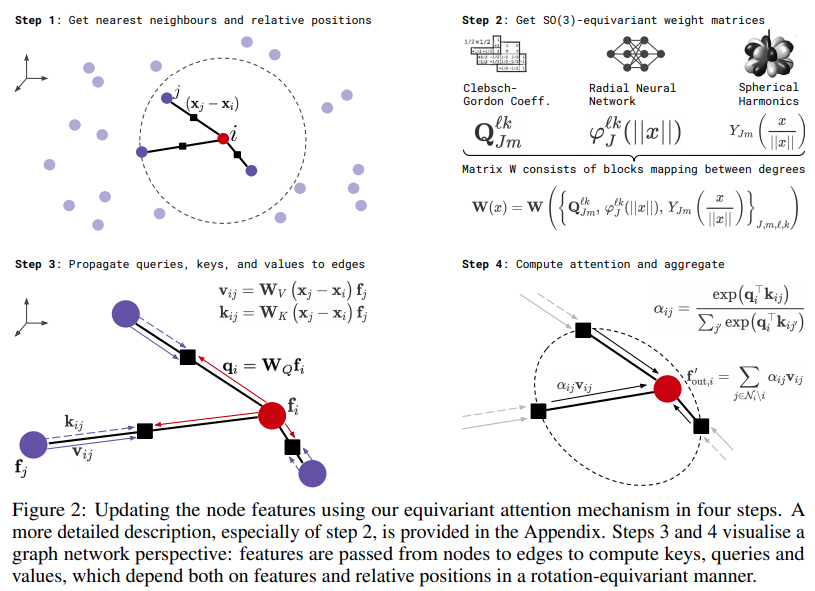
Implementación de SE3-Transformers para Autoatención Equivariante, en Pytorch. Puede ser necesario para replicar los resultados de Alphafold2 y otras aplicaciones de descubrimiento de fármacos.

Ejemplo de equivarianza

Si había estado utilizando alguna versión de SE3 Transformers anterior a la versión 0.6.0, actualice. @MattMcPartlon ha descubierto un gran error si no estaba utilizando la configuración de vecinos dispersos de adyacencia y confiando en la funcionalidad de vecinos más cercanos

Actualización: se recomienda utilizar Equiformer en su lugar

Instalar

$ pip install se3-transformer-pytorch

Uso

 import torch
from se3_transformer_pytorch import SE3Transformer

model = SE3Transformer (
    dim = 512 ,
    heads = 8 ,
    depth = 6 ,
    dim_head = 64 ,
    num_degrees = 4 ,
    valid_radius = 10
)

feats = torch . randn ( 1 , 1024 , 512 )
coors = torch . randn ( 1 , 1024 , 3 )
mask  = torch . ones ( 1 , 1024 ). bool ()

out = model ( feats , coors , mask ) # (1, 1024, 512)

Ejemplo de uso potencial en Alphafold2, como se describe aquí

 import torch
from se3_transformer_pytorch import SE3Transformer

model = SE3Transformer (
    dim = 64 ,
    depth = 2 ,
    input_degrees = 1 ,
    num_degrees = 2 ,
    output_degrees = 2 ,
    reduce_dim_out = True ,
    differentiable_coors = True
)

atom_feats = torch . randn ( 2 , 32 , 64 )
coors = torch . randn ( 2 , 32 , 3 )
mask  = torch . ones ( 2 , 32 ). bool ()

refined_coors = coors + model ( atom_feats , coors , mask , return_type = 1 ) # (2, 32, 3)

También puede dejar que la clase de transformador base se encargue de incorporar las características de tipo 0 que se pasan. Suponiendo que sean átomos

 import torch
from se3_transformer_pytorch import SE3Transformer

model = SE3Transformer (
    num_tokens = 28 ,       # 28 unique atoms
    dim = 64 ,
    depth = 2 ,
    input_degrees = 1 ,
    num_degrees = 2 ,
    output_degrees = 2 ,
    reduce_dim_out = True
)

atoms = torch . randint ( 0 , 28 , ( 2 , 32 ))
coors = torch . randn ( 2 , 32 , 3 )
mask  = torch . ones ( 2 , 32 ). bool ()

refined_coors = coors + model ( atoms , coors , mask , return_type = 1 ) # (2, 32, 3)

Si cree que la red podría beneficiarse aún más de la codificación posicional, puede caracterizar sus posiciones en el espacio y pasarla de la siguiente manera.

 import torch
from se3_transformer_pytorch import SE3Transformer

model = SE3Transformer (
    dim = 64 ,
    depth = 2 ,
    input_degrees = 2 ,
    num_degrees = 2 ,
    output_degrees = 2 ,
    reduce_dim_out = True  # reduce out the final dimension
)

atom_feats  = torch . randn ( 2 , 32 , 64 , 1 ) # b x n x d x type0
coors_feats = torch . randn ( 2 , 32 , 64 , 3 ) # b x n x d x type1

# atom features are type 0, predicted coordinates are type 1
features = { '0' : atom_feats , '1' : coors_feats }
coors = torch . randn ( 2 , 32 , 3 )
mask  = torch . ones ( 2 , 32 ). bool ()

refined_coors = coors + model ( features , coors , mask , return_type = 1 ) # (2, 32, 3) - equivariant to input type 1 features and coordinates 

Bordes

Para ofrecer información de borde a los transformadores SE3 (por ejemplo, tipos de enlaces entre átomos), solo tiene que pasar dos argumentos de palabras clave más en la inicialización.

 import torch
from se3_transformer_pytorch import SE3Transformer

model = SE3Transformer (
    num_tokens = 28 ,
    dim = 64 ,
    num_edge_tokens = 4 ,       # number of edge type, say 4 bond types
    edge_dim = 16 ,             # dimension of edge embedding
    depth = 2 ,
    input_degrees = 1 ,
    num_degrees = 3 ,
    output_degrees = 1 ,
    reduce_dim_out = True
)

atoms = torch . randint ( 0 , 28 , ( 2 , 32 ))
bonds = torch . randint ( 0 , 4 , ( 2 , 32 , 32 ))
coors = torch . randn ( 2 , 32 , 3 )
mask  = torch . ones ( 2 , 32 ). bool ()

pred = model ( atoms , coors , mask , edges = bonds , return_type = 0 ) # (2, 32, 1)

Si desea pasar valores continuos para sus bordes, puede optar por no configurar num_edge_tokens , codificar sus tipos de enlaces discretos y luego conectarlos a las características de Fourier de estos valores continuos.

 import torch
from se3_transformer_pytorch import SE3Transformer
from se3_transformer_pytorch . utils import fourier_encode

model = SE3Transformer (
    dim = 64 ,
    depth = 1 ,
    attend_self = True ,
    num_degrees = 2 ,
    output_degrees = 2 ,
    edge_dim = 34           # edge dimension must match the final dimension of the edges being passed in
)

feats = torch . randn ( 1 , 32 , 64 )
coors = torch . randn ( 1 , 32 , 3 )
mask  = torch . ones ( 1 , 32 ). bool ()

pairwise_continuous_values = torch . randint ( 0 , 4 , ( 1 , 32 , 32 , 2 ))  # say there are 2

edges = fourier_encode (
    pairwise_continuous_values ,
    num_encodings = 8 ,
    include_self = True
) # (1, 32, 32, 34) - {2 * (2 * 8 + 1)}

out = model ( feats , coors , mask , edges = edges , return_type = 1 )

Vecinos escasos

Si conoce la conectividad de sus puntos (digamos que está trabajando con moléculas), puede pasar una matriz de adyacencia, en forma de máscara booleana (donde True indica conectividad).

 import torch
from se3_transformer_pytorch import SE3Transformer

model = SE3Transformer (
    dim = 32 ,
    heads = 8 ,
    depth = 1 ,
    dim_head = 64 ,
    num_degrees = 2 ,
    valid_radius = 10 ,
    attend_sparse_neighbors = True ,  # this must be set to true, in which case it will assert that you pass in the adjacency matrix
    num_neighbors = 0 ,               # if you set this to 0, it will only consider the connected neighbors as defined by the adjacency matrix. but if you set a value greater than 0, it will continue to fetch the closest points up to this many, excluding the ones already specified by the adjacency matrix
    max_sparse_neighbors = 8         # you can cap the number of neighbors, sampled from within your sparse set of neighbors as defined by the adjacency matrix, if specified
)

feats = torch . randn ( 1 , 128 , 32 )
coors = torch . randn ( 1 , 128 , 3 )
mask  = torch . ones ( 1 , 128 ). bool ()

# placeholder adjacency matrix
# naively assuming the sequence is one long chain (128, 128)

i = torch . arange ( 128 )
adj_mat = ( i [:, None ] <= ( i [ None , :] + 1 )) & ( i [:, None ] >= ( i [ None , :] - 1 ))

out = model ( feats , coors , mask , adj_mat = adj_mat ) # (1, 128, 512)

También puede hacer que la red derive automáticamente los vecinos de enésimo grado con una palabra clave adicional num_adj_degrees . Si desea que el sistema diferencie entre el grado de los vecinos como información de borde, pase además un adj_dim distinto de cero.

 import torch
from se3_transformer_pytorch . se3_transformer_pytorch import SE3Transformer

model = SE3Transformer (
    dim = 64 ,
    depth = 1 ,
    attend_self = True ,
    num_degrees = 2 ,
    output_degrees = 2 ,
    num_neighbors = 0 ,
    attend_sparse_neighbors = True ,
    num_adj_degrees = 2 ,    # automatically derive 2nd degree neighbors
    adj_dim = 4             # embed 1st and 2nd degree neighbors (as well as null neighbors) with edge embeddings of this dimension
)

feats = torch . randn ( 1 , 32 , 64 )
coors = torch . randn ( 1 , 32 , 3 )
mask  = torch . ones ( 1 , 32 ). bool ()

# placeholder adjacency matrix
# naively assuming the sequence is one long chain (128, 128)

i = torch . arange ( 128 )
adj_mat = ( i [:, None ] <= ( i [ None , :] + 1 )) & ( i [:, None ] >= ( i [ None , :] - 1 ))

out = model ( feats , coors , mask , adj_mat = adj_mat , return_type = 1 )

Para tener un control preciso sobre la dimensionalidad de cada tipo, puede usar las palabras clave hidden_fiber_dict y out_fiber_dict para pasar un diccionario con el grado para dimensionar los valores como clave/valores.

 import torch
from se3_transformer_pytorch import SE3Transformer

model = SE3Transformer (
    num_tokens = 28 ,
    dim = 64 ,
    num_edge_tokens = 4 ,
    edge_dim = 16 ,
    depth = 2 ,
    input_degrees = 1 ,
    num_degrees = 3 ,
    output_degrees = 1 ,
    hidden_fiber_dict = { 0 : 16 , 1 : 8 , 2 : 4 },
    out_fiber_dict = { 0 : 16 , 1 : 1 },
    reduce_dim_out = False
)

atoms = torch . randint ( 0 , 28 , ( 2 , 32 ))
bonds = torch . randint ( 0 , 4 , ( 2 , 32 , 32 ))
coors = torch . randn ( 2 , 32 , 3 )
mask  = torch . ones ( 2 , 32 ). bool ()

pred = model ( atoms , coors , mask , edges = bonds )

pred [ '0' ] # (2, 32, 16)
pred [ '1' ] # (2, 32, 1, 3) 

Vecinos

Puede controlar aún más qué nodos se pueden considerar pasando una máscara de vecino. Todos los valores False se ocultarán para no tener en cuenta.

 import torch
from se3_transformer_pytorch . se3_transformer_pytorch import SE3Transformer

model = SE3Transformer (
    dim = 16 ,
    dim_head = 16 ,
    attend_self = True ,
    num_degrees = 4 ,
    output_degrees = 2 ,
    num_edge_tokens = 4 ,
    num_neighbors = 8 ,      # make sure you set this value as the maximum number of neighbors set by your neighbor_mask, or it will throw a warning
    edge_dim = 2 ,
    depth = 3
)

feats = torch . randn ( 1 , 32 , 16 )
coors = torch . randn ( 1 , 32 , 3 )
mask  = torch . ones ( 1 , 32 ). bool ()
bonds = torch . randint ( 0 , 4 , ( 1 , 32 , 32 ))

neighbor_mask = torch . ones ( 1 , 32 , 32 ). bool () # set the nodes you wish to be masked out as False

out = model (
    feats ,
    coors ,
    mask ,
    edges = bonds ,
    neighbor_mask = neighbor_mask ,
    return_type = 1
)

Nodos globales

Esta característica le permite pasar vectores que pueden verse como nodos globales que son vistos por todos los demás nodos. La idea sería agrupar su gráfico en algunos vectores de características, que se proyectarán en claves/valores en todas las capas de atención de la red. Todos los nodos tendrán acceso completo a la información global del nodo, independientemente de los vecinos más cercanos o del cálculo de adyacencia.

 import torch
from torch import nn
from se3_transformer_pytorch import SE3Transformer

model = SE3Transformer (
    dim = 64 ,
    depth = 1 ,
    num_degrees = 2 ,
    num_neighbors = 4 ,
    valid_radius = 10 ,
    global_feats_dim = 32 # this must be set to the dimension of the global features, in this example, 32
)

feats = torch . randn ( 1 , 32 , 64 )
coors = torch . randn ( 1 , 32 , 3 )
mask  = torch . ones ( 1 , 32 ). bool ()

# naively derive global features
# by pooling features and projecting
global_feats = nn . Linear ( 64 , 32 )( feats . mean ( dim = 1 , keepdim = True )) # (1, 1, 32)

out = model ( feats , coors , mask , return_type = 0 , global_feats = global_feats )

Hacer:

• Permitir que los nodos globales atiendan a todos los demás nodos, para darle a la red un conducto global para la información. (Similar a BigBird, ETC, Longformer, etc.)

autorregresivo

Puedes usar SE3 Transformers de forma autorregresiva con solo una bandera adicional

 import torch
from se3_transformer_pytorch import SE3Transformer

model = SE3Transformer (
    dim = 512 ,
    heads = 8 ,
    depth = 6 ,
    dim_head = 64 ,
    num_degrees = 4 ,
    valid_radius = 10 ,
    causal = True          # set this to True
)

feats = torch . randn ( 1 , 1024 , 512 )
coors = torch . randn ( 1 , 1024 , 3 )
mask  = torch . ones ( 1 , 1024 ). bool ()

out = model ( feats , coors , mask ) # (1, 1024, 512) 

Funciones experimentales

Claves convolucionadas no por pares

Descubrí que el uso de claves proyectadas linealmente (en lugar de la convolución por pares) parece funcionar bien en una tarea de eliminación de ruido de un juguete. Esto conduce a un ahorro de memoria del 25%. Puedes probar esta función configurando linear_proj_keys = True

 import torch
from se3_transformer_pytorch import SE3Transformer

model = SE3Transformer (
    dim = 64 ,
    depth = 1 ,
    num_degrees = 4 ,
    num_neighbors = 8 ,
    valid_radius = 10 ,
    splits = 4 ,
    linear_proj_keys = True # set this to True
). cuda ()

feats = torch . randn ( 1 , 32 , 64 ). cuda ()
coors = torch . randn ( 1 , 32 , 3 ). cuda ()
mask  = torch . ones ( 1 , 32 ). bool (). cuda ()

out = model ( feats , coors , mask , return_type = 0 )

Claves/valores compartidos entre todos los jefes

Existe una técnica relativamente desconocida para los transformadores en la que se puede compartir un encabezado de clave/valor en todos los encabezados de las consultas. En mi experiencia en PNL, esto generalmente conduce a un peor rendimiento, pero si realmente necesita intercambiar memoria por más profundidad o mayor número de grados, esta puede ser una buena opción.

 import torch
from se3_transformer_pytorch import SE3Transformer

model = SE3Transformer (
    dim = 64 ,
    depth = 8 ,
    num_degrees = 4 ,
    num_neighbors = 8 ,
    valid_radius = 10 ,
    splits = 4 ,
    one_headed_key_values = True  # one head of key / values shared across all heads of the queries
). cuda ()

feats = torch . randn ( 1 , 32 , 64 ). cuda ()
coors = torch . randn ( 1 , 32 , 3 ). cuda ()
mask  = torch . ones ( 1 , 32 ). bool (). cuda ()

out = model ( feats , coors , mask , return_type = 0 )

Clave/valores vinculados

También puede vincular la clave/valores (que sean iguales), para ahorrar la mitad de la memoria.

 import torch
from se3_transformer_pytorch import SE3Transformer

model = SE3Transformer (
    dim = 64 ,
    depth = 8 ,
    num_degrees = 4 ,
    num_neighbors = 8 ,
    valid_radius = 10 ,
    splits = 4 ,
    tie_key_values = True # set this to True
). cuda ()

feats = torch . randn ( 1 , 32 , 64 ). cuda ()
coors = torch . randn ( 1 , 32 , 3 ). cuda ()
mask  = torch . ones ( 1 , 32 ). bool (). cuda ()

out = model ( feats , coors , mask , return_type = 0 )

Usando EGNN

Esta es una versión experimental de EGNN que funciona para tipos superiores y mayor dimensionalidad que solo 1 (para las coordenadas). El nombre de la clase sigue siendo SE3Transformer ya que reutiliza cierta lógica preexistente, así que ignórelo por ahora hasta que lo borre más tarde.

 import torch
from se3_transformer_pytorch import SE3Transformer

model = SE3Transformer (
    dim = 32 ,
    num_neighbors = 8 ,
    num_edge_tokens = 4 ,
    edge_dim = 4 ,
    num_degrees = 4 ,       # number of higher order types - will use basis on a TCN to project to these dimensions
    use_egnn = True ,       # set this to true to use EGNN instead of equivariant attention layers
    egnn_hidden_dim = 64 ,  # egnn hidden dimension
    depth = 4 ,             # depth of EGNN
    reduce_dim_out = True  # will project the dimension of the higher types to 1
). cuda ()

feats = torch . randn ( 2 , 32 , 32 ). cuda ()
coors = torch . randn ( 2 , 32 , 3 ). cuda ()
bonds = torch . randint ( 0 , 4 , ( 2 , 32 , 32 )). cuda ()
mask  = torch . ones ( 2 , 32 ). bool (). cuda ()

refinement = model ( feats , coors , mask , edges = bonds , return_type = 1 ) # (2, 32, 3)

coors = coors + refinement  # update coors with refinement

Si desea especificar dimensiones individuales para cada uno de los tipos superiores, simplemente pase hidden_fiber_dict donde el diccionario está en el formato {<grado>:<dim>} en lugar de num_degrees

 import torch
from se3_transformer_pytorch import SE3Transformer

model = SE3Transformer (
    dim = 32 ,
    num_neighbors = 8 ,
    hidden_fiber_dict = { 0 : 32 , 1 : 16 , 2 : 8 , 3 : 4 },
    use_egnn = True ,
    depth = 4 ,
    egnn_hidden_dim = 64 ,
    egnn_weights_clamp_value = 2 , 
    reduce_dim_out = True
). cuda ()

feats = torch . randn ( 2 , 32 , 32 ). cuda ()
coors = torch . randn ( 2 , 32 , 3 ). cuda ()
mask  = torch . ones ( 2 , 32 ). bool (). cuda ()

refinement = model ( feats , coors , mask , return_type = 1 ) # (2, 32, 3)

coors = coors + refinement  # update coors with refinement 

Escalado (wip)

Esta sección enumerará los esfuerzos en curso para mejorar un poco la escala del transformador SE3.

En primer lugar, agregué redes reversibles. Esto me permite agregar un poco más de profundidad antes de encontrarme con los obstáculos habituales de la memoria. La preservación de la equivarianza se demuestra en las pruebas.

 import torch
from se3_transformer_pytorch import SE3Transformer

model = SE3Transformer (
    num_tokens = 20 ,
    dim = 32 ,
    dim_head = 32 ,
    heads = 4 ,
    depth = 12 ,             # 12 layers
    input_degrees = 1 ,
    num_degrees = 3 ,
    output_degrees = 1 ,
    reduce_dim_out = True ,
    reversible = True       # set reversible to True
). cuda ()

atoms = torch . randint ( 0 , 4 , ( 2 , 32 )). cuda ()
coors = torch . randn ( 2 , 32 , 3 ). cuda ()
mask  = torch . ones ( 2 , 32 ). bool (). cuda ()

pred = model ( atoms , coors , mask = mask , return_type = 0 )

loss = pred . sum ()
loss . backward ()

Ejemplos

Primero instale sidechainnet

$ pip install sidechainnet

Luego ejecute la tarea de eliminación de ruido de la columna vertebral de proteínas.

$ python denoise.py

Almacenamiento en caché

De forma predeterminada, los vectores base se almacenan en caché. Sin embargo, si alguna vez es necesario borrar el caché, simplemente debe establecer el indicador ambiental CLEAR_CACHE en algún valor al iniciar el script.

$ CLEAR_CACHE=1 python train.py

O puede intentar eliminar el directorio de caché, que debería existir en

$ rm -rf ~ /.cache.equivariant_attention

También puede designar su propio directorio donde desea que se almacenen los cachés, en el caso de que el directorio predeterminado tenga problemas de permisos.

CACHE_PATH=./path/to/my/cache python train.py

Pruebas

$ python setup.py pytest

Crédito

Esta biblioteca es en gran medida una adaptación del repositorio oficial de Fabian, pero sin la biblioteca DGL.

Citas

 @misc { fuchs2020se3transformers ,
    title   = { SE(3)-Transformers: 3D Roto-Translation Equivariant Attention Networks } , 
    author  = { Fabian B. Fuchs and Daniel E. Worrall and Volker Fischer and Max Welling } ,
    year    = { 2020 } ,
    eprint  = { 2006.10503 } ,
    archivePrefix = { arXiv } ,
    primaryClass = { cs.LG }
}

 @misc { satorras2021en ,
    title   = { E(n) Equivariant Graph Neural Networks } ,
    author  = { Victor Garcia Satorras and Emiel Hoogeboom and Max Welling } ,
    year    = { 2021 } ,
    eprint  = { 2102.09844 } ,
    archivePrefix = { arXiv } ,
    primaryClass = { cs.LG }
}

 @misc { gomez2017reversible ,
    title     = { The Reversible Residual Network: Backpropagation Without Storing Activations } ,
    author    = { Aidan N. Gomez and Mengye Ren and Raquel Urtasun and Roger B. Grosse } ,
    year      = { 2017 } ,
    eprint    = { 1707.04585 } ,
    archivePrefix = { arXiv } ,
    primaryClass = { cs.CV }
}

 @misc { shazeer2019fast ,
    title   = { Fast Transformer Decoding: One Write-Head is All You Need } ,
    author  = { Noam Shazeer } ,
    year    = { 2019 } ,
    eprint  = { 1911.02150 } ,
    archivePrefix = { arXiv } ,
    primaryClass = { cs.NE }
}