El riesgo es un juego de tableros de estrategia de diplomacia, conflicto y conquista para dos a seis jugadores. El giro gira entre los jugadores que controlan ejércitos de juego con las que intentan capturar territorios de otros jugadores, con resultados determinados por los rollos de dados. El objetivo del juego es ocupar cada territorio en el tablero y al hacerlo, eliminar a los otros jugadores. Cada turno consta de dos acciones:
El propósito de este proyecto ha sido implementar el juego de riesgo con algunos cambios realizados en las reglas y diseñar un agente artificialmente inteligente que pueda jugar el juego correctamente y tener muchas posibilidades de ganar cuando se enfrentan a otros oponentes, incluidos los dos humanos reales. jugadores u otros jugadores de agentes.
El juego se implementa utilizando el lenguaje de programación Java. Controlar giros, realizar acciones solicitadas por el jugador, actualizar el mapa del juego, verificar si todo está sucediendo de acuerdo con las reglas, etc., son las cosas que hace esta parte del código. La interfaz de usuario del juego también está diseñada a través de archivos .fxml que extraen el mapa y es la plataforma que conecta el reproductor con la lógica del juego.
Esta sección se centra en la implementación y evaluación de heurísticas que conducen a una fuerte IA para el riesgo del juego.
La implementación se basa en el algoritmo de poda Minax Alpha-beta. El jugador construye un árbol de predicción basado en el algoritmo DFS.
Cada vez que es el turno del agente para jugar, se hace un árbol. Los nodos de los árboles son los estados del juego (mapa del juego en ese estado) y cada borde es un posible ataque realizado desde el estado actual para atacar el estado de resultados del mapa. Una acción de ataque consiste en las coordenadas de los territorios iniciales y objetivo y el número de unidades elegidas para estar en el ejército de ataque. El nodo raíz es el estado actual del mapa que un jugador tiene que elegir desde. Aunque, el árbol no puede predecir hasta el estado final del juego debido a una gran cantidad de posibles movimientos que un jugador puede tener en cada estado que la memoria y los límites de tiempo no permiten. Por lo tanto, el jugador solo puede construir el árbol a una cierta profundidad que hemos definido en el código. También hay algunas simplificaciones aplicadas a partes particulares de la estrategia de juego del agente que se explicarán en las siguientes secciones. Para tomar la mejor decisión posible, las heurísticas se definen para los nodos más profundos posibles (hojas de árbol) que evalúan cuánto alcanzar ese estado puede ser beneficioso para el jugador. Dicha heurística se explicará más a fondo en el informe. Cuando se determinan los valores de las hojas, el árbol se transmitirá a la poda Minax Alpha-beta y este conocido algoritmo encontrará la mejor serie de acciones que el jugador puede tener.
El suministro de unidades a los territorios puede ser una tarea difícil; En el sentido de que queremos mejorar nuestro poder de ataque, pero también nos aseguramos de tener suficiente poder de defensa en los territorios que están en peligro de ser atacados. El despliegue de unidades en países adyacentes a los territorios enemigos podría ser una forma inteligente de mantener el equilibrio entre estos dos objetivos.
Borrador de simplificación:
Predictar e incluir todos los posibles escenarios de borrador en el árbol de predicción conducirá a un árbol complejo que enfrentaría los problemas mencionados anteriormente; Por lo tanto, una de las simplificaciones hechas es que utilizamos una heurística de redacción que siempre tiene el mejor resultado posible y predice que los oponentes también hacen este enfoque en la redacción; En otras palabras, eliminamos los resultados de la redacción, ya que las posibilidades forman el árbol de predicción y los cambiamos a escenarios de borrador definitivos.
Para hacerlo, tomamos los siguientes pasos:
Borrador heurístico:
Paso 1:
Aking la suma de todas las unidades en los países enemigos adyacentes al país X dará una medida que llamamos Amenazas de Seguridad Fronteriza (BST) en X.
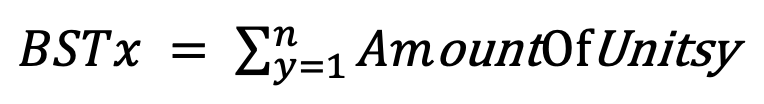
Paso 2:
Dividir este BST por las unidades situadas en X proporciona una relación de seguridad fronteriza (BSR) que puede compararse entre todos los países fronterizos.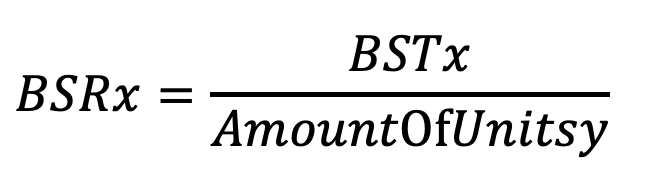
Los países con un alto BSR tienen más probabilidades de ser conquistados por un jugador enemigo, ya que el número de unidades enemigas en los países enemigos adyacentes es relativamente mayor que el número de unidades en el país mismo. Elegir países con un alto BSR para suministrar aumentará su fuerza defensiva al reducir la BSR. El suministro de unidades a los países con un BSR más bajo, lo que significa que ya tienen una mejor postura defensiva, aumentará su fuerza ofensiva, lo que aumenta las posibilidades de un ataque exitoso de estos países.
Paso 3:
Normalización del BSR dividiéndolo por la suma de todos los BSR de países, un jugador posee, dará una medición directa por la cual alguien podría organizar unidades. La relación de seguridad fronteriza normalizada (NBSR) se calcula por: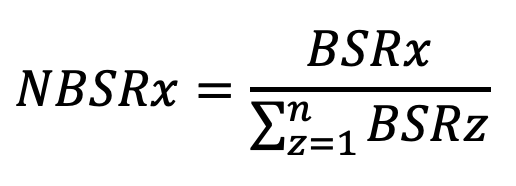
Da una relación directa de cómo las unidades podrían distribuirse entre los países. En este punto, podemos ver que habría un problema con estas relaciones porque algunos datos son irrelevantes, y no queremos agregar unidades a todos nuestros territorios, por lo que establecemos un umbral entre los pasos dos y tres clasificando los datos de BSRX en Una orden descendente (nos estamos centrando más en fortalecer el poder de defensa), dividir los datos del medio y establecer los números en la mitad inferior a cero.
Paso 4: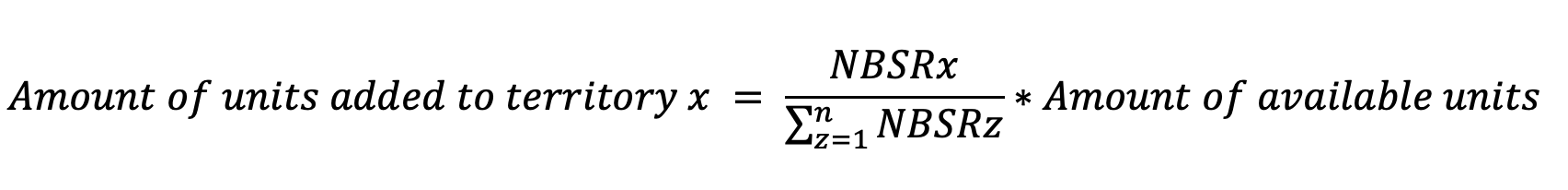
El paso 4 continuará hasta que no queden más unidades disponibles para agregar.
Hay algunas simplificaciones aplicadas en la fase de ataque para hacer que el árbol sea menos complicado para que podamos predecir en niveles más profundos de él. Esto se puede hacer verificando qué escenarios de ataque tienen una mayor oportunidad de ganar la batalla y solo incluirlos en el árbol.
Para evaluar cuán beneficiosa es una hoja de árbol para ese jugador específico; Hemos definido cuatro características heurísticas que se encuentran sus mejores pesos posibles durante el aprendizaje de la heurística que se explicará más adelante. Todas las características devuelven un resultado entre cero a uno porque cuando las características se valoran en relaciones cercanas entre sí, el aprendizaje y la asignación de peso serían más precisos.
Las características son:
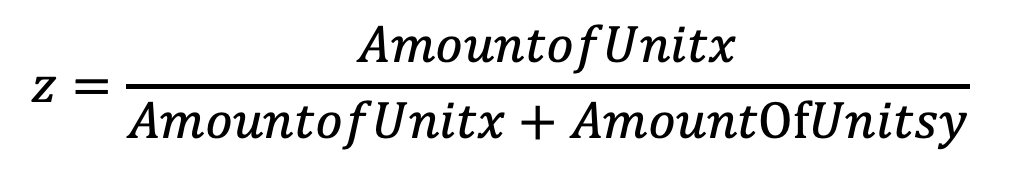
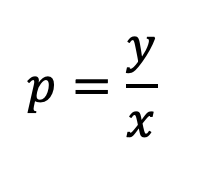
Dar peso a cada una de las heurísticas en la parte anterior ayuda a evaluar cuán importante e influyente es cada un agente para ganar el juego. El proceso de encontrar estos pesos es a través de la genética y el aprendizaje. Cada gen es un conjunto de cuatro pesos para esas cuatro características. Comenzamos generando 100 conjuntos de pesos aleatorios en el rango [0,10]. Después de eso, ocurrirán 10 torneos. Para cada torneo, se seleccionarán al azar 10 genes de la población primaria. Todos los pares posibles de genes jugarán entre sí y se documentará el resultado de cada juego en cada torneo. La función de aptitud física se define como (número de victorias / número de juegos) para cada gen. Se seleccionarán los tres genes superiores en cada torneo (basado en la función de acondicionamiento físico), por lo que ahora tenemos 30 genes seleccionados superiores. Entre estos seleccionamos 12 pares aleatorios y para cada par realizamos un crossover que está creando un nuevo gen calculando el peso promedio del par de genes. Por lo tanto, ahora tenemos 12 nuevos genes de este crossover. Por otro lado, 3 genes se seleccionan al azar dentro de los 30 genes que teníamos y los mutan cambiando un peso aleatorio de cada uno a otro peso aleatorio en el rango [0,10]. Después de todo esto, ahora tenemos 15 genes nuevos que se colocan en la población primaria, reemplazando a los 15 menos buenos que ya teníamos allí. En este punto se genera la segunda generación de genes. Este proceso continuará repitiendo hasta que se generen la generación 4 de genes. El gen superior en esa población se seleccionará como nuestros mejores pesos para las características de nuestra heurística que el agente usará para jugar.