Noise Reduction
1.0.0
Sobre el proyecto
Pila de tecnología
Estructura de archivo
Empezando
Resultados y demostración
Trabajo futuro
Colaboradores
Agradecimientos y recursos
Licencia
El ruido debía eliminarse, que se induce naturalmente como el ruido no ambiental que se elimina con la señalización de la señal. Consulte esta documentación también este blog sobre la reducción de ruido de IA
Se utiliza la biblioteca de la biblioteca para la manupulación de audio.
Para las señales de audio usamos scipy
Matplotlib utilizado para manipular los datos y visualizar la señal.
El resto es numpy para las operaciones matemáticas, ondea para operar en el archivo de onda.
Noise Reduction ├───docs ## Documents and Images │ └───Input Audio file ├─── Project Details │ | │ ├─── │ │ ├───Research papers │ │ ├───Linear Algebra │ │ ├───Neural networks & Deep Learning │ │ ├───Project Documentation │ │ ├───AI Noise Reduction Blog │ │ ├───AI Noise Reduction Report │ │ └───Code Implementation │ │ ├───AI Noise Reduction.py │ │ ├───audio.wav │ │ ├───Resources
Probado en Windows
clon git https://github.com/dhriti03/noise-reduction.gitcd ruido-reducción
En su cuaderno, instale ciertas bibliotecas
onda de instalación de pip PIP install Librosa PIP install scipy.io PIP Instalar matplotlib.pyplot
*Este es el archivo de audio original *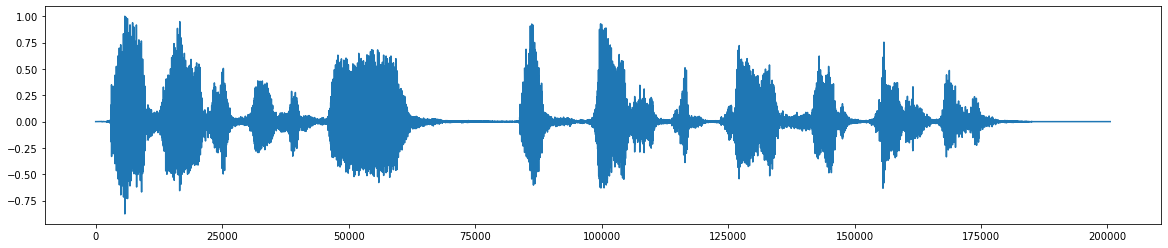 
*Después de la adición del ruido * 
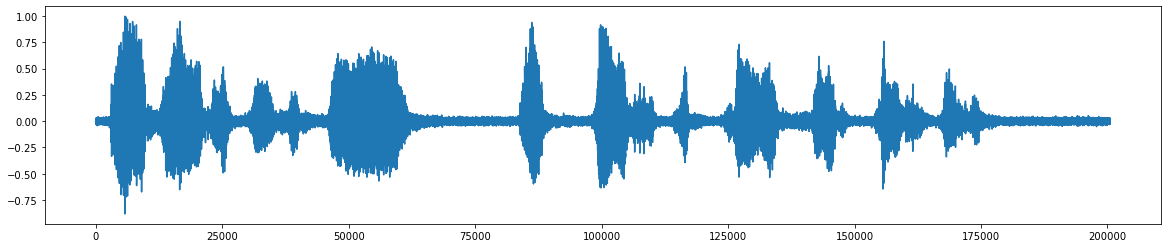*La señal de audio final después de eliminar el ruido * 
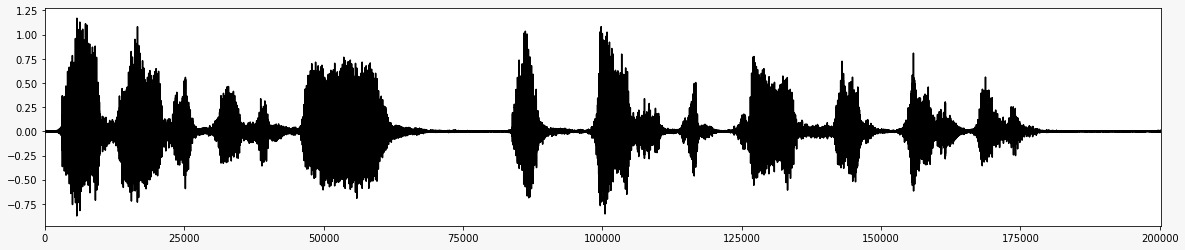*Diagrama de flujo para el proyecto *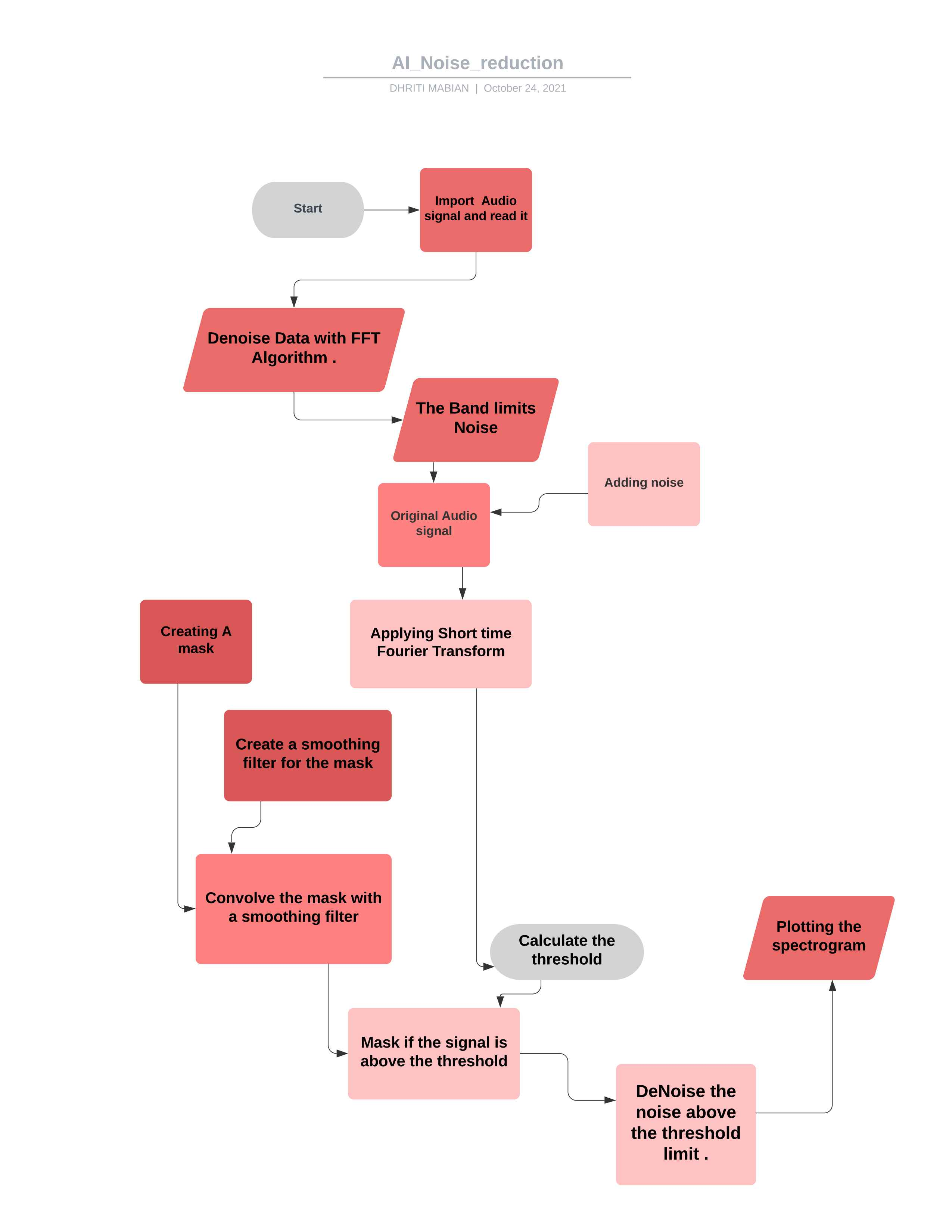 
Al manipular el código de acuerdo con sus requisitos, puede usarlo para controlar la mayoría de los letrales de audio. ##Teoría
Se calcula un FFT sobre el clip de audio de ruido
Las estadísticas se calculan sobre FFT del ruido (en frecuencia)
Se calcula un umbral en función de las estadísticas del ruido (y la sensibilidad deseada del algoritmo)
Se determina una máscara comparando la señal FFT con el umbral
La máscara se suaviza con un filtro sobre frecuencia y tiempo
La máscara está apacada en la FFT de la señal y está invertida
import iPython de scipy.io import wavfileImport scipy.signalImport numpy como npimport matplotlib.pyplot como pltimpport librosaimport wave%matplotlib inline en línea
Aquí estamos importando las bibliotecas como el Ipython Lib utilizado para crear un entorno integral para la informática interactiva y exploratoria.
De la biblioteca Scipy.io se utiliza para manipular los datos y la visualización de los datos utilizando una amplia gama de comandos de Python.
Numpy contiene una matriz multidimensional y estructuras de datos de matriz. Se puede utilizar para realizar una serie de operaciones matemáticas en matrices como rutinas trigonométricas, estadísticas y algebraicas, por lo tanto, es una biblioteca muy útil.
La biblioteca matplotlib.pyplot ayuda a comprender la gran cantidad de datos a través de diferentes visualizaciones.
Librosa usó cuando trabajamos con datos de audio como en la generación de música (usando LSTM), reconocimiento automático de voz. Proporciona los bloques de construcción necesarios para crear los sistemas de recuperación de información musical.
%Matplotlib en línea para habilitar el trazado en línea, donde los gráficos/gráficos se mostrarán justo debajo de la celda donde se escriben sus comandos de trazado. Proporciona interactividad con el backend en los frontends como el cuaderno Jupyter.
wav_loc = r '/home/ruido_reduction/downloads/wave/file.wav'rate, data = wavfile.read (wav_loc, mmap = false)
Aquí tomamos la ubicación de la ruta del archivo WAW y luego leemos ese archivo WAW con el módulo de archivo de onda que es de la biblioteca Scipy.io . con parámetros (nombre de archivo - cadena o mango de archivo abierto que es un archivo WAV de entrada). Luego el (mmap: bool, opcional en el que leer datos como mapeado de memoria (predeterminado: falso).
def fftnoise (f): f = np.array (f, dtype = "complejo") np = (len (f) - 1) // 2fases = np.random.rand (np) * 2 * np.piphases = np .cos (fases) + 1j * np.sin (fases) F [1: np + 1] * = fasesf [-1: -1 -np: -1] = np.conj (f [1: np + 1] ) return np.fft.ifft (f) .real
Aquí, en primer lugar, definimos la función de ruido FFT en resumen, una transformación rápida de Fourier (FFT) es un algoritmo que calcula la transformación discreta de Fourier (DFT) de una secuencia, o su inverso (IDFT). El análisis de Fourier convierte una señal de su dominio original (a menudo tiempo o espacio) a una representación en el dominio de frecuencia y viceversa. El DFT se obtiene descomponiendo una secuencia de valores en componentes de diferentes frecuencias.
Usando la transformación rápida de Fourier y definiendo una función del complejo de tipo de datos y finalmente calculando la parte real de la función. En esto, las frecuencias que varían entre la frecuencia mínima y la frecuencia máxima se establecen en 1 y el descanso no deseado se descuida.
Dar la ubicación del archivo
Leer el archivo WAV
-32767 a +32767 es un audio adecuado (para ser simétrico) y 32768 significa que el audio recortado en ese punto
WAV-File es entero de 16 bits, el rango es [-32768, 32767], dividiendo así por 32768 (2^15) dará el rango adecuado de TwoS-Complement de [-1, 1]
Def Band_Limited_Noise (min_freq, max_freq, muestras = 1024, muestlate = 1): freqs = np.abs (np.fft.fftfreq (muestras, 1 / sample)) f = np.zeros (muestras) f [np.Logical_and (freqs > = min_freq, freqs <= max_freq)] = 1return fftnoise (f)
Una función o serie de tiempo cuya transformación de Fourier está restringida a un rango finito de frecuencias o longitudes de onda.
Definición de la frecuencia con la frecuencia estándar con el límite MIN y MAX.
ruido_len = 2 # SecondSnoise = Band_Limited_Noise (min_freq = 4000, max_freq = 12000, muestras = len (data), muestlerate = tasa)*10noise_clip = ruido [: tasa*ruido_len] audio_clip_band_limited = data+ruido
El bloque de ruido blanco limitado por banda especifica un espectro de dos lados, donde las unidades son Hz.
donde se compara el máximo de 12000 y min frek de 4000 WRT el ruido y los datos proporcionados.
Aquí estamos recortando la señal de ruido al tener un producto de la velocidad y la len de la señal de ruido.
Agregar así el ruido y los datos dados
En efecto, agregar ruido expande el tamaño del conjunto de datos de entrenamiento.
Se agrega ruido aleatorio a las variables de entrada que las hacen diferentes cada vez que se expone al modelo.
Agregar ruido a las muestras de entrada es una forma simple de aumento de datos.
Agregar ruido significa que la red es menos capaz de memorizar muestras de entrenamiento porque están cambiando todo el tiempo,
dando como resultado pesos de red más pequeños y una red más robusta que tiene un error de generalización más bajo.
Importar tiempo de entrada a partir de la vez, la importación de Timedelta como TD
Tiempo de importación Este módulo proporciona varias funciones relacionadas con el tiempo. Para la funcionalidad relacionada, consulte también los módulos de fecha y hora y calendario. clase DateTeTime.timedelta
Una duración que expresa la diferencia entre las instancias de dos fecha, hora o de fecha y hora de la resolución de microsegundos.
def _stft (y, n_fft, hop_length, win_length): return librosa.stft (y = y, n_fft = n_fft, hop_length = hop_length, win_length = win_length)
Se puede usar la transformación de Fourier de corto tiempo para cuantificar el cambio de la frecuencia de una señal no estacionaria y el contenido de fase con el tiempo.
La longitud del lúpulo debe referirse al número de muestras entre marcos sucesivos. Para el análisis de la señal, la longitud del lúpulo debe ser menor que el tamaño del marco, de modo que los marcos se superponen.
Parámetros ynp.ndarray [shape = (n,)], señal de entrada de valor real
n_fftint> 0 [escalar]
Longitud de la señal de ventana después del relleno con ceros. El número de filas en la matriz STFT D es (1 + n_fft/2) . El valor predeterminado, N_FFT = 2048 muestras, corresponde a una duración física de 93 milisegundos a una frecuencia de muestreo de 22050 Hz, es decir, la velocidad de muestra predeterminada en Librosa. Este valor está bien adaptado para señales de música. Sin embargo, en el procesamiento del habla, el valor recomendado es 512, correspondiente a 23 milisegundos a una frecuencia de muestreo de 22050 Hz. En cualquier caso, recomendamos configurar N_FFT en una potencia de dos para optimizar la velocidad del algoritmo de transformación de Fourier (FFT) rápida.
hop_lengthint> 0 [escalar]
Número de muestras de audio entre columnas STFT adyacentes.
Los valores más pequeños aumentan el número de columnas en D sin afectar la resolución de frecuencia del STFT.
Si no se especifica, el valor predeterminado se gana a Win_Length // 4 (ver más abajo).
win_lengthint <= n_fft [escalar]
Cada cuadro de audio está ventana por ventana de longitud win_length y luego se acaricia con ceros para que coincida con n_fft .
Los valores más pequeños mejoran la resolución temporal del STFT (es decir, la capacidad de discriminar los impulsos que están estrechamente espaciados en el tiempo) a expensas de la resolución de frecuencia (es decir, la capacidad de discriminar los tonos puros que están estrechamente espaciados en frecuencia). Este efecto se conoce como la compensación de localización de frecuencia de tiempo y debe ajustarse de acuerdo con las propiedades de la señal de entrada y.
Si no se especifica, el valor predeterminado a win_length = n_fft .
return librarsA.istft (y, hop_length, win_length)
Transformación inversa de Fourier a corto plazo (ISTFT). Convertida el espectrograma de valor complejo STFT_MATRIX a la serie de tiempo y minimizando el error medio cuadrado entre stft_matrix y stft de y como se describe en
En general, la función de la ventana, la longitud del lúpulo y otros parámetros deben ser los mismos que en STFT, lo que conduce principalmente a una reconstrucción perfecta de una señal de stft_matrix no modificada.
def _amp_to_db (x): return librosa.core.amplitude_to_db (x, ref = 1.0, Amin = 1e-20, top_db = 80.0)
1. Convertir un espectrograma de amplitud al espectrograma de escala de DB. Esto es equivalente a Power_TO_DB (S ** 2), pero se proporciona por conveniencia.
return librarsA.core.db_to_amplitude (x, ref = 1.0)
Convierta un espectrograma escala de DB a un espectrograma de amplitud.
Esto invierte efectivamente amplitud_to_db:
db_to_amplitude (s_db) ~ = 10.0 (0.5* (s_db + log10 (ref)/10)) **
def trapt_spectrogram (señal, título): Fig, ax = plt.subplots (figSize = (20, 4)) cax = ax.matshow (señal, origen = "menor", aspecto = "auto", cmap = plt.cm. sísmico, vmin = -1 * np.max (np.abs (señal)), vmax = np.max (np.abs (señal)),
)Traficando el speclograma con señal como entrada.
La clase Axes contiene la mayoría de los elementos de figura: eje, garrapata, línea2d, texto, polígono, etc., y establece el sistema de coordenadas.
Proporciona múltiples mapas de color en matplotlib accesible a través de esta función. O encuentre una buena representación en el espacio de colores 3D para su conjunto de datos.
Fig.ColorBar (Cax) ax.set_title (título)
La mejor manera de ver lo que está sucediendo es agregar una barra de color (plt.colorbar (), después de crear el diagrama de dispersión). Observará que sus valores externos entre 0 y 10000 están por debajo de la parte más baja de la barra, donde las cosas son muy claras.
En general, los valores debajo de Vmin se colorearán con el color más bajo, y los valores por encima de VMAX obtendrán el color más alto.
Si establece VMAX más pequeño que Vmin, internamente se cambiarán. Aunque, dependiendo de la versión exacta de Matplotlib y las funciones precisas llamadas, Matplotlib podría dar una advertencia de error. Por lo tanto, es mejor establecer Vmin siempre más bajo que VMAX.
def trapt_statistics_and_filter (medo_freq_noise, std_freq_noise, ruido_thresh, suaveing_filter): fig, ax = plt.subplots (ncols = 2, figsize = (20, 4)) PLT_STD, = ax [0] .Plot (std_freq_nois de ruido ")
plt_std, = ax [0] .plot (ruido_thresh, etiqueta = "umbral de ruido (por frecuencia)") ax [0] .set_title ("umbral para la máscara")
ax [0] .legend () cax = ax [1] .matshow (suave_filter, origin = "inferior") fig.colorbar (cax) ax [1] .set_title ("Filtro para suavizar la máscara")Rapas estadísticas básicas de reducción de ruido.
La relación señal/ruido (SNR o S/N) es una medida utilizada en ciencia e ingeniería que compara el nivel de una señal deseada con el nivel de ruido de fondo.
La SNR se define como la relación de potencia de señal para la potencia de ruido, a menudo expresada en decibelios.
Una relación superior a 1: 1 (mayor que 0 dB) indica más señal que ruido.
Configuración de la frecuencia de umbral para el enmascaramiento de ruido.
El umbral de enmascaramiento se refiere a un proceso donde un sonido se hace inaudible debido a la presencia de otro sonido.
Entonces, el umbral de enmascaramiento es el nivel de presión de sonido de un sonido necesario para hacer que el sonido sea audible en presencia de otro ruido llamado "enmascarador"
Así agregó el umbral.
Señales de ruido de desenfoque con varios filtros de pase bajo
Aplicar filtros hechos a medida a las imágenes (convolución 2D)
def removenOise ( # para promediar la señal (voltaje) de la porción de pendiente positiva (aumento) de una onda triangular para tratar de eliminar el mayor ruido posible. Audio_clip, # Estos clips son los parámetros utilizados en los que haríamos los respectivos Operaciones ruido_clip, n_grad_freq = 2, # cuántos canales de frecuencia suavizar con la máscara.n_grad_time = 4, # cuántos canales de tiempo suavizar con la máscara.n_fft = 2048, # número de audio de los marcos entre las columnas STFT.win_length = 2048, # Cada cuadro de audio está ventana por `Window ()`. n_std_thresh = 1.5, # cuántas desviaciones estándar más fuertes que la DB media del ruido (en cada nivel de frecuencia) que se considerará señalProp_Decrease = 1.0, # en qué medida debe disminuir el ruido (1 = todo, 0 = Ninguno) Verbose = falso , # La bandera le permite escribir expresiones regulares que parecen presentables Visual = false, # si traza los pasos del algoritmo):
Def removeneoise ( para promediar la señal (voltaje) de la porción de pendiente positiva (aumento) de una onda triangular para tratar de eliminar la mayor cantidad de ruido posible.
audio_clip,
Estos clips son los parámetros utilizados en los que haríamos las operaciones respectivas
ruido_clip, n_grad_freq = 2 cuántos canales de frecuencia suavizar con la máscara.
n_grad_time = 4, cuántos canales de tiempo suavizar con la máscara.
n_fft = 2048
Número de audio de marcos entre columnas STFT.
win_length = 2048, cada cuadro de audio está ventana por window() . La ventana será de longitud win_length y luego acolchada con ceros para que coincida con n_fft ..
hop_length = 512, número de audio de cuadros entre columnas STFT.
n_std_thresh = 1.5 ¿Cuántas desviaciones estándar más fuertes que la DB media del ruido (en cada nivel de frecuencia) que se considerará señal
prop_decrease = 1.0, en qué medida debe disminuir el ruido (1 = todo, 0 = ninguno)
textualmente = falso,
El indicador le permite escribir expresiones regulares que se ven presentables visual = false, #si traza los pasos del algoritmo):
ruido_stft = _stft (Noise_clip, n_fft, hop_length, win_length) Noise_stft_db = _amp_to_db (np.abs (ruido_stft)))
Stft sobre el ruido
Convertir a DB
Mean_freq_noise = np.mean (ruido_stft_db, axis = 1) std_freq_noise = np.std (ruido_stft_db, axis = 1) Noise_thresh = Mean_freq_noise + std_freq_noise * n_std_thresh
Calcule las estadísticas sobre el ruido
Aquí estamos por el ruido de umbral, agregamos la media y el ruido estándar y el ruido N_STD.
Sig_stft = _stft (audio_clip, n_fft, hop_length, win_length) SIG_STFT_DB = _AMP_TO_DB (NP.ABS (SIG_STFT))
STFT sobre señal
Mask_gain_db = np.min (_amp_to_db (np.abs (sig_stft))))
Calcular el valor para enmascarar DB a
suave_filter = np.outer (np.concatenate (
[np.linspace (0, 1, n_grad_freq + 1, endpoint = false), np.linspace (1, 0, n_grad_freq + 2),
]
) [1: -1], np.concatenate (
[np.linspace (0, 1, n_grad_time + 1, endpoint = false), np.linspace (1, 0, n_grad_time + 2),
]
) [1: -1],
) suave_filter = suave_filter / np.sum (suave_filter)Cree un filtro de suavizado para la máscara en el tiempo y la frecuencia
db_ththresh = np.repeat (np.reshape (ruido_ththresh, [1, len (Mean_freq_noise)]), np.shape (sig_STFT_DB) [1], axis = 0,
) .TCalcule el umbral para cada contenedor de frecuencia/tiempo
Sig_Mask = Sig_stft_DB <db_ththresh
máscara para la señal
Sig_Mask = scipy.signal.fftconvolve (Sig_Mask, Smoothing_filter, Mode = "Igual") SIG_MASK = SIG_MASK * PROP_DECREASE
Convolución de máscara con filtro de liso
# mask the signalsig_stft_db_masked = (sig_stft_db * (1 - sig_mask)+ np.ones(np.shape(mask_gain_dB)) * mask_gain_dB * sig_mask) # mask realsig_imag_masked = np.imag(sig_stft) * (1 - sig_mask)sig_stft_amp = (_db_to_amp (SIG_STFT_DB_MASKED) * np.sign (sig_STFT)) + (1J * SIG_IMAG_MASKED)
Enmascarar la señal
# Recupere el SignalRecovered_Signal = _istft (Sig_stft_amp, Hop_Length, Win_Length) Recounded_spec = _amp_to_db (np.abs (_stft (Recounded_signal, n_fft, hop_length, win_length))))
)recuperar la señal
Por lo tanto, aplique una máscara si la señal está por encima del umbral
Convolucionar la máscara con un filtro de suavizado
Aplicando el algoritum de reducción de ruido para el archivo WAV ya descargado.
Aplicando el FFT sobre la grabación en vivo de la señal de audio.
Además, una implementación más profunda de la IA para la cancelación de ruido.
Aplicación del algoritum de reducción de ruido para varios formatos de archivos de audio.
La señal de audio en vivo con el micrófono y ESP32 y, por lo tanto, obtendrá el archivo WAV para el cálculo adicional y el procesamiento de la señal.
Dhriti mabiano
Priyal awankar
*SRA VJTI_EKLAVYA 2021
Shreyas atre
Shah duro
Audacia
Método de cancelación de ruido
Tomó la caldera de Martin Heinz
Tim Sainburg
Licencia
