Las pruebas de equivalencia se pueden aplicar para evaluar si un efecto observado de un predictor individual en un modelo de regresión múltiple es lo suficientemente pequeño como para considerarse estadística y prácticamente insignificante (Alter y Counsell, 2021). Para obtener más información, consulte la página de OSF y/o una preimpresión gratuita disponible en Psyarxiv.
Las siguientes funciones ofrecen alternativas apropiadas basadas en la equivalencia para concluir el efecto insignificante entre un predictor y el resultado en la regresión múltiple
Estas funciones R están diseñadas para acomodar múltiples contextos de investigación sin esfuerzo, con o sin acceso al conjunto de datos completo. Las dos funciones, reg.equiv.fd() y reg.equiv() , proporcionan una salida similar pero difieren en el tipo de información de entrada requerida por el usuario.
Específicamente, la primera función, reg.equiv.fd() , requiere el conjunto de datos y el modelo de datos completos en R (objeto lm ), mientras que el segundo no. reg.equiv() está destinado a investigadores que no tienen acceso al conjunto de datos completo, pero aún así desean evaluar la falta de asociación de un cierto predictor con la variable de resultado en regresión múltiple, por ejemplo, utilizando información típicamente presentada en una sección de resultados o Tabla reportada en un artículo publicado.
reg.equiv.fd() : requerido el conjunto de datos completodatfra= un marco de datos (por ejemplo, MTCARS)model= el modelo, un objeto LM (por ejemplo, mod1 , donde mod1<- mpg~hp+cyl )delta= el tamaño del efecto más pequeño del interés (Sesoi), tamaño de efecto mínimamente significativo (MMES) o límite superior del intervalo de equivalencia (?) (Eg, .15)predictor= el nombre del predictor a probar (por ejemplo, "cyl" )test= Tipo de prueba se establece automáticamente en dos pruebas unilaterales (Tost; Schuirmann, 1987), la otra opción es el Anderson-Hauck (Ah; Anderson y Hauck, 1983)std= el delta (o, sesoi) es el conjunto como estandarizado por defecto. Indica std=FALSE para asumir unidades no estandarizadasalpha= La tasa de error nominal de tipo I se establece en .05 por defecto. Para cambiar, simplemente indique el nivel alfa. Por ejemplo, alpha=.10 reg.equiv.fd() Ejemplo: 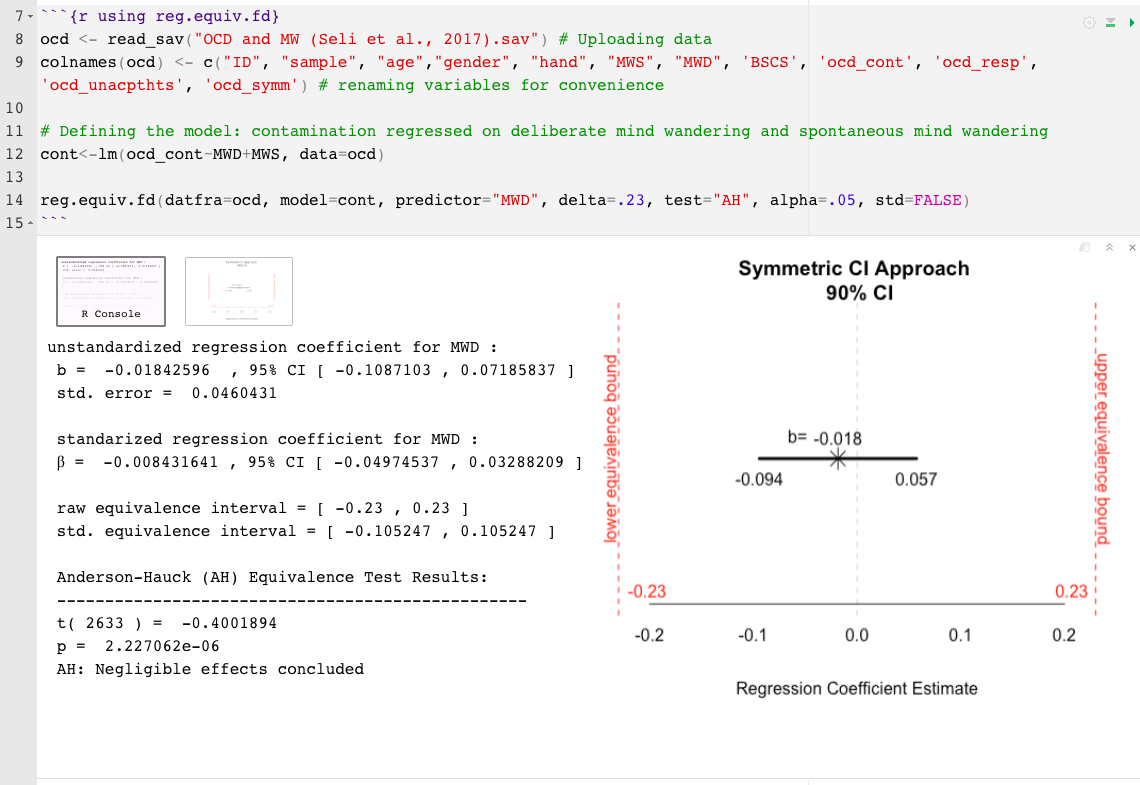
reg.equiv() : no se requiere un conjunto de datos completob= El tamaño del efecto estimado asociado con el predictor de interés, esto podría estar estandarizado o no estandarizado (por ejemplo, .02)se= El error estándar asociado con el tamaño del efecto del predictor de interés (si el tamaño del efecto está estandarizado, asegúrese de que el valor se esté vinculado al efecto estandarizado y no en bruto)p= El número de predictores totales en el modelo de regresión (excluyendo la intersección)n= tamaño de muestradelta= el tamaño del efecto más pequeño del interés (Sesoi), tamaño de efecto mínimamente significativo (MMES) o límite superior del intervalo de equivalencia (?) (Eg, .15)predictor= el nombre del predictor a probar (por ejemplo, "cyl" )test= Tipo de prueba se establece automáticamente en dos pruebas unilaterales (Tost; Schuirmann, 1987), la otra opción es el Anderson-Hauck (Ah; Anderson y Hauck, 1983)std= el delta (o, sesoi) y el tamaño del efecto indicado se establecen como estandarizados de forma predeterminada. Indica std=FALSE para asumir unidades no estandarizadasalpha= La tasa de error nominal de tipo I se establece en .05 por defecto. Para cambiar, simplemente indique el nivel alfa. Por ejemplo, alpha=.10 reg.equiv() Ejemplo: 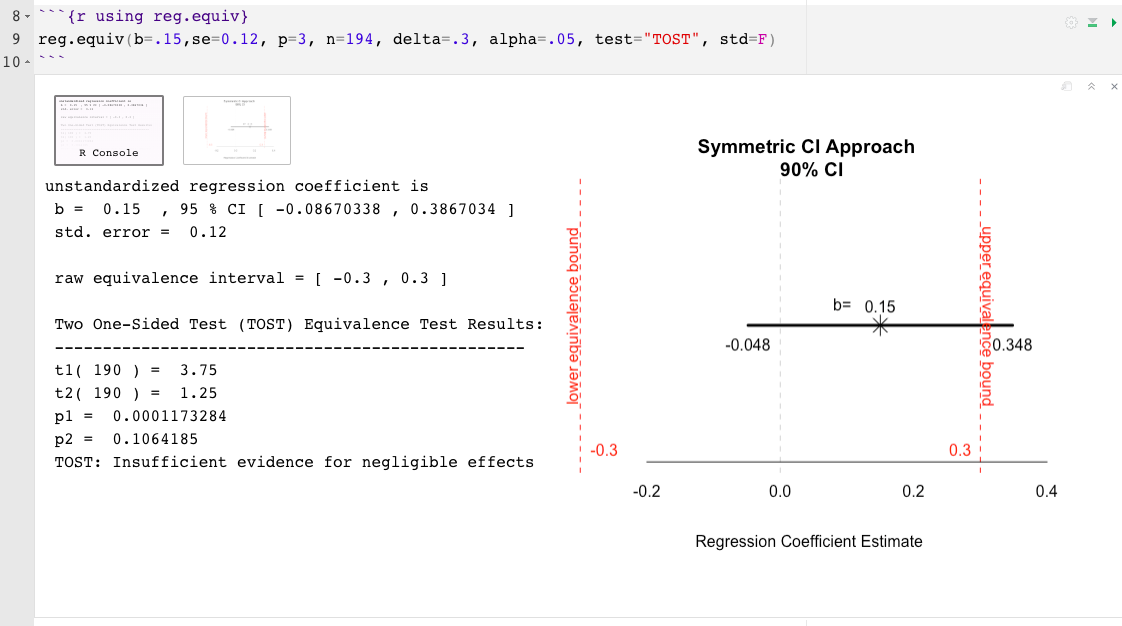
La prueba de equivalencia es un método diseñado dentro del marco de prueba de significancia de hipótesis nula (NHST). NHST ha sido muy criticado por su dependencia excesiva en los resultados dicotómicos de los valores de P con poca o ninguna consideración de la magnitud del efecto o sus implicaciones en la práctica (por ejemplo, Cumming, 2012; Fidler y Loftus, 2009; Harlow, 1997; Kirk, 2003 ; Lee, 2016 2014). Los investigadores deben tener en cuenta las limitaciones de la NHST y desenredar los aspectos prácticos y estadísticos de los resultados de la prueba.
Para minimizar las limitaciones de los valores de P , es más informativo interpretar la magnitud y precisión del efecto observado más allá de la conclusión de "efectos insignificantes" o "evidencia insuficiente de efectos insignificantes". Los efectos observados deben interpretarse en relación con los límites de equivalencia, el alcance de su incertidumbre y sus implicaciones prácticas (o falta de ellos) . Por esta razón, las dos funciones R ofrecidas aquí también incluyen una representación gráfica del efecto observado y su incertidumbre asociada en relación con el intervalo de equivalencia. La gráfica resultante ayuda a ilustrar qué tan cerca, lejos y ancho o estrecho, el efecto observado y su margen de error están de los límites de equivalencia; Inferir sobre la proporción y la posición de la banda de confianza en relación con el intervalo de equivalencia puede ayudar a interpretar los resultados por encima y por encima de los valores de P.