Este proyecto se ha movido para aumentar (matemáticas/diferenciación/autodiff) y este repositorio ya no se está actualizando.
| Rama | Traver | Appveyor | CodeCov.io |
|---|---|---|---|
master | |||
develop |
Autodiff es una biblioteca C ++ de encabezado que facilita la diferenciación automática (modo de avance) de las funciones matemáticas de variables individuales y múltiples.
Esta implementación se basa en la expansión de la serie Taylor de una función analítica F en el punto x₀ :
La idea esencial de Autodiff es la sustitución de números con polinomios en la evaluación de F (X₀) . Al sustituir el número X₀ con el polinomio de primer orden x₀+ε , y usando el mismo algoritmo para calcular F (x₀+ε) , el polinomio resultante en ε contiene los derivados de la función F '(x₀) , f' '(x₀) , f '' '(x₀) , ... dentro de los coeficientes. Cada coeficiente es igual a la derivada de su orden respectivo, dividido por el factorial de la orden.
Con mayor detalle, suponga que uno está interesado en calcular las primeras n derivadas de F en X₀ . Sin pérdida de precisión al cálculo de los derivados, todos los términos O (ε n+1 ) que incluyen poderes de ε mayores que N pueden descartarse. (Esto se debe al hecho de que cada término en un polinomio depende solo de los términos iguales y de orden inferior bajo operaciones aritméticas). Según estas reglas de truncamiento, F proporciona una transformación polinomial a polinomio:
La capacidad de C ++ para sobrecargar operadores y funciones permite la creación de una clase fvar que representa polinomios en ε . Por lo tanto, el mismo algoritmo F que calcula el valor numérico de y₀ = f (x₀) , cuando se escribe para aceptar y devolver variables de un tipo genérico (plantilla), también se usa para calcular el polinomio ʃ n y n εⁿ = f (x₀++ ε) . ¡Los derivados f (n) (x₀) se encuentran a partir del producto del respectivo factorial n! y coeficiente y n :

#include <boost/math/diferenciation/autodiff.hpp> #include <iostream> Template <typename t>
T cuarto_power (t const & x) {
T x4 = x * x; // Retval en el operador*() usa la memoria de X4 a través de NRVO.
x4 *= x4; // No se realizan copias de x4 dentro del operador*= () incluso cuando se cuadra.
regresar x4; // x4 usa la memoria de Y en main () a través de nrvo.} int main () {usando el espacio de nombres boost :: math :: diferenciation;
orden unsigned de constexpr = 5; // Derivado de orden más alto para ser calculado.
auto const x = make_fvar <double, orden> (2.0); // encontrar derivados en x = 2.
Auto const y = cuarto_power (x); para (unsigned i = 0; i <= orden; ++ i)
std :: cout << "y.derivative (" << i << ") =" << y.derivative (i) << std :: endl; regresar 0;
}/*Salida: y.derivative (0) = 16y.derivative (1) = 32y.derivative (2) = 48y.derivative (3) = 48y.derivative (4) = 24y.derivative (5) = 0*/Lo anterior calcula
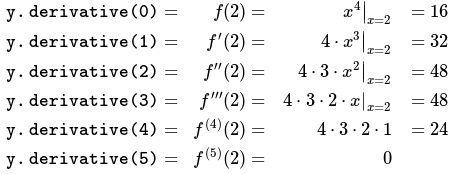
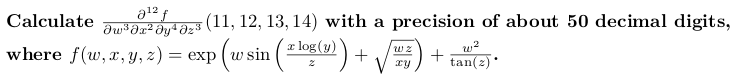
#include <boost/math/diferenciation/autodiff.hpp> #include <boost/multiprecision/cpp_bin_float.hpp> #include <iostream> Usando el espacio de nombres boost :: math :: diferenciación; plantilla <typename w, typename x, typename y,, Typename Z>
Promocione <W, X, Y, Z> F (const W&W, const x & x, const y & y, const z & z) {usando el espacio de nombres std;
return exp (w * sin (x * log (y) / z) + sqrt (w * z / (x * y))) + w * w / tan (z);
} int main () {usando float50 = boost :: multipecision :: cpp_bin_float_50; constexpr unsigned nw = 3; // orden máximo de derivados para calcular W para W
constexpr unsigned nx = 2; // orden máximo de derivados para calcular para x
constexpr unsigned ny = 4; // orden máximo de derivados para calcular y
constexpr unsigned nz = 3; // orden máximo de derivados para calcular z
// Declarar 4 variables independientes juntas en un std :: tuple.
Auto const variables = make_ftuple <float50, nw, nx, ny, nz> (11, 12, 13, 14); auto const & w = std :: get <0> (variables); // hasta los derivados de NW en W = 11
auto const & x = std :: get <1> (variables); // Hasta los derivados nx en x = 12
auto const & y = std :: get <2> (variables); // hasta los derivados de NY en y = 13
auto const & z = std :: get <3> (variables); // hasta los derivados de NZ en z = 14
auto const V = f (w, x, y, z); // calculado a partir de la diferenciación simbólica de Mathematica.
Float50 Const Respuesta ("1976.319600747797717779881875290418720908121189218755");
std :: cout << std :: setprecision (std :: numeric_limits <float50> :: dígitos10)
<< "Mathematica:" << Respuesta << 'n' << "Autodiff:" << V.Derivative (NW, NX, NY, NZ) << 'n' << std :: setprecision (3)
<< "Error relativo:" << (v.derivative (nw, nx, ny, nz) / respuesta - 1) << 'n'; regresar 0;
}/*Salida: Mathematica: 1976.3196007477977177798818752904187209081211892188autodiff: 1976.3196007477797717777988187529041872090812118921888reler #include <boost/math/diferenciation/autodiff.hpp> #include <iostream> usando el espacio de nombres boost :: math :: constants; usando el espacio de nombres boost :: math :: diferenciation; // Las ecuaciones y la función/nombres variables son de // https://en.wikipedia.org/wiki/Greeks_(finance)#Formulas_FOR_EUROPEA_OPTION_GREEKS// Distribución acumulativa normal estándar FunctionTemplate <typename x>
X phi (x const & x) {return 0.5 * erfc (-one_div_root_two <x> () * x);
} enum clase CP {call, put}; // asume cero rendimiento de dividendos anuales (q = 0) .template <typename Price, typename Sigma, typename tau, typename tasa>
Promocione <Price, Sigma, Tau, Tarife> Black_Scholes_option_Price (CP CP, Double K,
Precio const & s,
Sigma Const y Sigma,
Tau const y tau,
Tasa const & r) {usando el espacio de nombres std;
auto const d1 = (log (s / k) + (r + sigma * sigma / 2) * tau) / (sigma * sqrt (tau)); auto const d2 = (log (s / k) + (r - sigma * sigma / 2) * tau) / (sigma * sqrt (tau)); switch (cp) {case cp :: llamada: return s * phi (d1)-exp (-r * tau) * k * phi (d2); case cp :: put: return exp (-r * tau) * k * Phi (-d2)-s * phi (-d1);
}
} int main () {doble const k = 100.0; // precio de ejercicio.
auto const s = make_fvar <double, 2> (105); // Precio de acciones.
doble const Sigma = 5; // volatilidad.
doble const tau = 30.0 / 365; // Tiempo de vencimiento en años. (30 días).
doble const r = 1.25 / 100; // tasa de interés.
Auto const call_price = Black_scholes_option_price (cp :: call, k, s, sigma, tau, r); Auto const put_price = Black_scholes_option_price (cp :: put, k, s, sigma, tau, r);
std :: cout << "Black-Scholes Call Price =" << Call_price.derivative (0) << 'n' << "Black-Scholes Put Price =" << PUT_PRICE.DERIVATIVO (0) << 'N' << "llamar delta =" << call_price.derivative (1) << 'n' << "poner delta =" << put_price.derivative (1) << 'n' << "llamar gamma =" << call_price .derivative (2) << 'n' << "poner gamma =" << put_price.derivative (2) << 'n'; regresar 0;
}/*Salida: Black-Scholes Price de llamada = 56.5136black-Scholes Put Precio = 51.4109Call delta = 0.773818put delta = -0.226182call gamma = 0.00199852put gamma = 0.00199852*///Consulte Ejemplo/Black_Scholes.cpp para una lista más amplia de griegos de opciones calculadas automáticamente.
Los ejemplos anteriores ilustran algunas de las ventajas de usar Autodiff:
Eliminación de la redundancia del código. La existencia de n funciones separadas para calcular derivadas es una forma de redundancia de código, con todos los pasivos que vienen con ella:
Los cambios en una función requieren N cambios adicionales a otras funciones. En el tercer ejemplo anterior, considere cuánto más grande e interdependiente sería la base de código anterior si se escribiera una función separada para cada valor griego.
Las dependencias de una función derivada para un propósito diferente se romperán cuando se realicen cambios en la función original. Lo que no necesita existir no puede romperse.
Hinchazón de código, reduciendo la integridad conceptual. El control sobre la evolución del código es más fácil/más seguro cuando la base del código es más pequeña y puede capaz de ser intuitiva.
Precisión de derivados sobre métodos de diferencia finita. Los métodos de diferencia finita de iteración única siempre incluyen una variable libre de Δx que debe elegirse cuidadosamente para cada aplicación. Si Δx es demasiado pequeño, entonces los errores numéricos se vuelven grandes. Si Δx es demasiado grande, entonces los errores matemáticos se vuelven grandes. Con Autodiff, no hay variables libres para establecerse y la precisión de la respuesta es generalmente superior a los métodos de diferencia finita, incluso con la mejor opción de Δx .
Los detalles adicionales están en el manual de Autodiff.
Distribuido bajo la licencia de software Boost, versión 1.0.
Solo encabezado.
Optimizado para C ++ 17. También se compila y probó con los estándares C ++ 11, C ++ 14 y propuesto C ++ 20.
Toda la memoria se asigna en la pila.
| Nombre | Objetivo |
|---|---|
doc | documentación |
example | ejemplos |
include | encabezado |
test | pruebas unitarias |
Informe de informes: asegúrese de mencionar la versión, la plataforma y el compilador de refuerzo que está utilizando. Una pequeña muestra de código compilable para reproducir el problema siempre es buena también.
Envíe sus parches como solicitudes de extracción contra la rama de desarrollo. Tenga en cuenta que al enviar parches, acepta licenciar sus modificaciones bajo la licencia de software Boost, versión 1.0.