Este artículo le brinda conocimientos relevantes sobre JavaScript, que presenta principalmente el contenido relevante sobre los tipos de números. Hay dos tipos de números en JavaScript: tipos numéricos y BigInt. Espero que le resulten útiles. ayuda.
[Recomendaciones relacionadas: videotutorial de javascript, interfaz web]
Hay dos tipos de números en JavaScript :
El tipo Number , que es un tipo numérico en el sentido convencional, se almacena en el formato IEEE-754 de 64 bits y es un "número de coma flotante de doble precisión". del tipo Number ;
El tipo BigInt representa números enteros de cualquier longitud. Normalmente no los usamos a menos que representen números distintos de 2 53 a -2 53. Presentaremos estos tipos de datos profesionales en detalle en capítulos posteriores;
La forma de escribir números es muy simple, pero JavaScrpt tiene muchos azúcares sintácticos convenientes y rápidos para que los usemos. Aprender estos azúcares sintácticos no solo mejorará nuestra capacidad de lectura de código, sino que también mejorará el sentido de alto nivel de nuestro código.
Los números decimales son los más simples y los usaremos más o menos en casi todos los artículos. Por ejemplo, creamos una variable y almacenamos 100 mil millones:
sea diez mil millones = 10000000000;
Aunque el funcionamiento es muy sencillo, hay un problema: es difícil contar cuántos 0 siguen 1 Si estamos escribiendo un código de transferencia, un 0 incorrecto puede llevarnos a la quiebra.
En este momento, podemos usar _ como delimitador, de la siguiente manera:
sea diez mil millones = 10_000_000_000;
El código anterior puede contar claramente el número de 0 , ¡que obviamente es la solución óptima!
_ guión bajo aquí es un azúcar sintáctico de JavaScript , que el motor ignorará durante la ejecución. Los dos métodos de escritura anteriores tienen el mismo efecto, pero la experiencia de lectura es muy diferente.
Circuito cerebral Qingqi
Algunos zapatos para niños tienen que preguntar, siempre he estado en grupos de 4 0 desde que era niño, ¿por qué tengo que agrupar 3 0 ? Por tanto, podemos escribirlo de la siguiente forma sin ningún problema:
sea diez mil millones = 100_0000_0000;
O podría escribirse así:
sea diez mil millones = 1_0000_0000_00;
Lo que quiero expresar aquí es que no importa qué método de división uses, no afectará el tamaño del número en sí. ¡Idea el método más poderoso!
Aunque usar _ puede dividir elegantemente muchos 0 , en la vida real generalmente no lo escribimos de esta manera. Por ejemplo, a menudo escribimos 10000000000 como "10 mil millones", por lo que se pueden omitir muchos 0 , reduciendo así la posibilidad de hacer. errores.
JavaScript también proporciona una manera de omitir 0 Podemos usar la letra e seguida de un número para representar el número 0 Por ejemplo:
let tenbillion = 1e10;//10 mil millones, 1 seguido de 10 0sconsole.log(3.14e9);//3140000000, seguido de 7 0, mire hacia abajo si tiene alguna pregunta.
La comprensión del código anterior es muy simple. e10 puede entenderse como 1_0000_0000_00 0 que es 1 seguido de 10 , por lo que podemos pensar:
1e10 === 1 * 1_0000_0000_00;//e10 significa 1 seguido de 10 03.14e9 === 3.14 * 1_000_000_000;//e9 significa 1 seguido de 9 0s
También podemos utilizar este método para representar números muy pequeños, como 1 nanómetro:
let nm = 0.000000001 //Unidad (metro)
Como hay demasiados 0 , también podemos usar _ :
sea nm = 0.000_000_001;
Por supuesto, también puedes usar e para omitir todos 0 , de la siguiente manera:
let nm = 1e-9;//9 0s a la izquierda de 1, incluido el que está antes del punto decimal
En otras palabras, e-9 significa 1 -9 , que es 1/1000_000_000 , por lo que la siguiente ecuación es verdadera:
1e-9 === 1/1_000_000_000;3.14e-8 === 3.14/1_000_000_00;
El hexadecimal es un formato comúnmente utilizado en programación, como color, codificación, etc. Podemos agregar 0x antes de números ordinarios para representar números hexadecimales:
let hex = 0xff;//255, no distingue entre mayúsculas y minúsculas, 0xFF es lo mismo
Los números binarios comienzan con 0b :
dejar bin = 0b1011;//11
Los números octales comienzan con 0o :
dejar oct = 0o777;//511
Este método de escritura simple solo admite estos tres tipos especiales. En cuanto a otros números base, puede usar funciones especiales para generarlos ( parseInt ).
El método toString puede convertir el número en una forma de cadena correspondiente a base .
Regala una castaña:
sea número = 996; console.log(num.toString(8));//Convertir a cadena octal console.log(num.toString(16));//Convertir a cadena hexadecimal console.log(num.toString( 32));// Convertir a 32 cadenas hexadecimales
Los resultados de la ejecución del código son los siguientes:
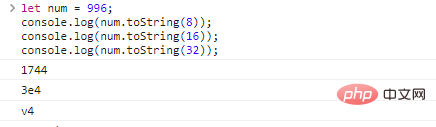
El rango de base puede ser de 2 a 36 Si no se completa, el valor predeterminado es 10 .
Tenga en cuenta que si usa números para llamar directamente al método toString , en algunos casos necesitará aplicar dos . por ejemplo:
console.log(123.toString(8));//Error, error de sintaxis console.log(123..toString(8));//Correcto, 173
Hay dos . después del número. Esto se debe a que en JavaScript el primer . después del número se considera el punto decimal y el segundo punto es el .
Si es decimal, este problema no existe. Por ejemplo:
console.log(3.14.toString(8));
O podemos usar paréntesis para evitar el uso de dos puntos, por ejemplo:
console.log((123).toString(8));//'173
El redondeo es una de las operaciones más comunes con números y suele incluir:
Redondear hacia abajo, Math.floor(num)
console.log(Math.floor(3.14));//3 console.log(Math.floor(9.99));//9 console.log(Math.floor(-3.14));//-4 console.log(Math.floor(-9.99));//-10
No siga el principio de redondeo y tome directamente el número entero más cercano menor o igual al valor actual.
Redondear hacia arriba, Math.ceil(num)
console.log(Math.ceil(3.14));//4 console.log(Math.ceil(9.99));//10 console.log(Math.ceil(-3.14));//-3 console.log(Math.ceil(-9.99));//-9
No siga el principio de redondeo y tome directamente el número entero más cercano mayor o igual al número actual.
Redondear al número entero más cercano, Math.round(num)
console.log(Math.round(3.14));//3 console.log(Math.round(9.99));//10 console.log(Math.round(-3.14));//-3 console.log(Math.round(-9.99));//-10
Siguiendo el principio de redondeo, se toma el número entero más cercano al número actual.
Eliminar decimales, Math.trunc(num)
console.log(Math.trunc(3.14));//3 console.log(Math.trunc(9.99));//9 console.log(Math.trunc(-3.14));//-3 console.log(Math.trunc(-9.99));//-9
Elimine directamente los números después del punto decimal y redondee a dígitos enteros. El navegador IE no admite este método
Compare los cuatro métodos anteriores:
| piso de matematicas | Matemáticas.ceil | Ronda de matemáticas | Matemáticas.trunc | |
|---|---|---|---|---|
| 3.14 | 3 | 4 | 3 | 3 |
| 9,99 | 9 | 10 | 10 | 9 |
| -3.14 | -4 | -3 | -3 | -3 |
| -9,99 | -10 | -9 | -10 | -9 |
El método anterior simplemente redondea el decimal a un número entero. En algunos casos, necesitamos decimales con una precisión específica. Por ejemplo, ¿qué debemos hacer si tomamos los últimos 4 dígitos de pi?
Hay dos métodos:
multiplicación matemática y conteo de división
let pi = 3.1415926;console.log(Math.round(pi * 10000) / 10000);//3.1416
El código anterior primero multiplica pi por 10000 , luego lo redondea y luego lo divide por 10000 , obteniendo así un resultado que cumple con los requisitos de precisión. Sin embargo, esto parece una tontería y JavaScript nos proporciona una manera más sencilla.
a fijo(n)
let pi = 3.1415926;console.log(pi.toFixed(4));//3.1416
El código anterior parece no tener ningún problema con la salida. De hecho, toFixed devuelve una cadena. Si necesitamos un tipo numérico, debemos convertirlo. Podemos usar el operador unario + pi.toFixed(4) .
Además, si la mantisa decimal no es lo suficientemente larga, toFixed agregará '0' al final:
let num = 3.1;console.log(num.toFixed(9));
Los resultados de la ejecución del código son los siguientes: 
Esto también prueba que el valor de retorno de toFixed es una cadena; de lo contrario, se omitirá 0 .
Las representaciones de coma flotante siempre están sesgadas en muchos casos.
Dentro de la computadora, los números de coma flotante se representan de acuerdo con IEEE-754 , donde los números de coma flotante de precisión simple son de 32 bits y los números de coma flotante de precisión doble son de 64 bits. En un número de coma flotante de doble precisión, se usa 1 bit para representar el signo, 52 bits se usan para almacenar los dígitos significativos y 11 bits se usan para almacenar la posición del punto decimal.
Aunque 64 bits ya pueden representar números muy grandes, todavía existe la posibilidad de cruzar el límite, por ejemplo:
let bigNum = 1e999;console.log(bigNum);//Infinito
El número que supere el valor máximo pasará a ser Infinity (infinito), perdiendo así el tamaño del número original, lo cual es una especie de desviación.
Hay otro tipo de desviación que debemos aprender:
console.log(0.1+0.2 === 0.3);//falseconsole.log(0.1 + 0.2);
Los resultados de la ejecución del código son los siguientes:
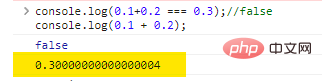
Así es, el resultado de 0.1 + 0.2 no es 0.3 , sino un montón de 0 seguidos de un 4 .
Este tipo de desviación es muy fatal, especialmente en centros comerciales y escenarios de trabajo bancario. Incluso una desviación muy pequeña conducirá a la pérdida de riqueza infinita en escenarios de alta rotación.
Una vez escuché una historia sobre un empleado de banco que robó millones de dólares deduciendo el salario de cada empleado ¡era sólo 20 centavos!
Creo que si esto me sucediera, definitivamente no podría encontrarlo, por eso es muy importante ser preciso en todo momento.
No sé si esta historia es cierta o no~~
Tomemos como ejemplo nuestro sistema decimal común. Todos sabemos que hay dos cosas raras en los decimales, una se llama decimales periódicos infinitos y la otra se llama decimales periódicos infinitos. Por ejemplo, 1/3 es un decimal periódico infinito. decimal 0.3333333(3) y pi Es un decimal infinito y no periódico. Infinito significa que el tamaño del número no se puede describir numéricamente claramente y lo que podemos escribir es inexacto.
También hay algunos números que se repiten infinitamente en binario. La diferencia es que en decimal, un número como 0.1 que parece muy simple, es un decimal de bucle infinito en binario.
Por ejemplo:
sea x = 0.1;console.log(x.toFixed(20));
Los resultados de la ejecución del código son los siguientes:
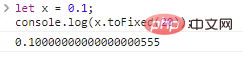
¿No crees que es increíble? Simplemente creamos una variable y le asignamos un valor de 0.1 y luego tomamos 20 decimales, pero obtuvimos un resultado increíble.
Si cambiamos el ángulo, puede que sea más fácil entender este fenómeno. En el sistema decimal, cualquier número entero dividido por 10 o 10 potencias enteras es un número normal y exacto, como por ejemplo 1/10 o 996/1000 . Sin embargo, si divide por 3 , obtendrá un resultado de bucle, como 1/3 .
Esta descripción también es válida si se convierte a binario.
En binario, cualquier número entero dividido por 2 o una potencia entera de 2 es un número exacto normal. Sin embargo, si lo divides por 10 , obtendrás un bucle infinito de números binarios.
Por lo tanto, podemos concluir que los números binarios no pueden representar con precisión 0.1 y 0.2 al igual que los decimales no pueden describir 1/3 .
Aviso:
Este tipo de desviación de datos no es un defecto de JavaScript; es el mismo resultado para PHP, Java, C, Perl y Ruby.
redondeo
Al mostrar un decimal infinitamente recurrente, podemos usar directamente el método toFixed para redondear el decimal. Este método devuelve directamente una cadena, lo cual es muy conveniente para mostrar precios.
0.3.toFixed(2);//0.30
Utilice unidades pequeñas
Otra forma es que podemos usar unidades más pequeñas para calcular precios y distancias, como usar centavos en lugar de yuanes para calcular el precio total. De hecho, muchos sitios web comerciales hacen esto. Sin embargo, este método solo reduce el número de apariciones de decimales y no hay forma de evitar por completo la aparición de decimales.
Hay dos valores especiales en los números JavaScript : Infinity y NaN .
¿Cómo juzgar si un número es un número normal?
Podemos utilizar dos métodos:
es finito (val)
Esta función convertirá el parámetro val a un tipo numérico, luego determinará si el número es finito y devolverá true cuando el número no sea NaN , Infinity o -Infinity .
console.log(isFinite(NaN));//falseconsole.log(isFinite(Infinity));//falseconsole.log(isFinite(3));//trueconsole.log(isFinite('12'));// verdadero Los resultados de la ejecución del código son los siguientes: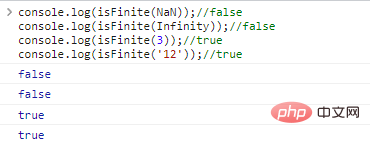
Dado que una cadena que no se puede convertir en un número se convertirá en NaN , podemos usar el método isFinite para determinar si la cadena es una cadena numérica:
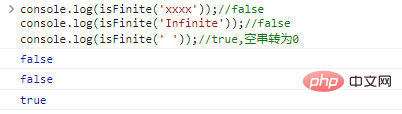
console.log(isFinite('xxxx'));//falseconsole.log(isFinite('Infinite'));//falseconsole.log(isFinite(' '));//true, la cadena vacía se convierte a 0Los resultados de la ejecución del código son los siguientes:
esNaN(val)
Devuelve true cuando val es NaN u otro valor que no se puede convertir en un número.
console.log(isNaN(NaN));//trueconsole.log(isNaN('Infinito'));//true Resultados de la ejecución del código: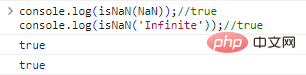
¿Por qué utilizar la función isNaN en lugar de leerla directamente?
Por ejemplo:
console.log(NaN === NaN);//falso
Los resultados de la ejecución del código son los siguientes:
Esto se debe a que NaN no es igual a ningún número, incluido él mismo.
Object.is(a,b) puede determinar si los parámetros a y b son iguales. Si son iguales, devuelve true ; de lo contrario, devuelve false . Sus resultados solo tienen tres situaciones:
Se puede comparar con NaN
console.log(Object.is(NaN,NaN));//verdadero
Resultados de la ejecución del código:

0 y -0
console.log(Object.is(0,-0));//falso
Resultados de la ejecución del código:

Dentro de la computadora, lo positivo y lo negativo están representados por 0 y 1 Debido a los diferentes signos, 0 y -0 son en realidad diferentes y se expresan de diferentes maneras.
otro
Otras situaciones de comparación son exactamente iguales a a === b .
parseInt y parseFloat pueden convertir cadenas en números. A diferencia de + y Number , sus restricciones son más flexibles. Por ejemplo, usar + y Number para una cadena como "100¥" inevitablemente devolverá NaN , pero parseInt y parseFloat pueden manejarlo fácilmente.
Por ejemplo:
console.log(+"100¥");console.log(parseInt("100¥"));console.log(parseFloat("12.5¥"));Resultados de la ejecución del código:
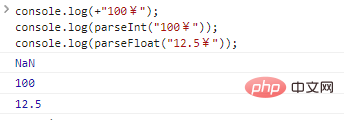
parseInt y parseFloat leen números de una cadena hasta que ya no se pueden leer. Ambos son particularmente adecuados para procesar cadenas que comienzan con números como "99px" y "11.4em" , pero se devuelve NaN para cadenas que comienzan con otros caracteres.
console.log(parseInt('ff2000'));//NaN Sin embargo, descubrimos ff2000 es en realidad una cadena digital hexadecimal. parseInt también puede manejar esta situación, pero necesita agregar un parámetro hexadecimal.
Por ejemplo:
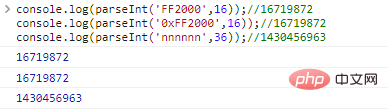
console.log(parseInt('FF2000',16));
//16719872
console.log(parseInt('0xFF2000',16));
//16719872
console.log(parseInt('nnnnnn',36));
//1430456963Resultados de la ejecución del código:
El objeto Math incorporado contiene muchas constantes y métodos que usamos con frecuencia. Estos son solo algunos ejemplos de los que se usan comúnmente:
Matemáticas.PI
Pi Π es una constante infinita no cíclica, podemos usar Math.PI en su lugar:
console.log(Math.PI);

Matemáticas.aleatorio()
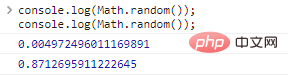
Genera un número aleatorio en el intervalo [0,1) :
console.log(Math.random());console.log(Math.random());
Si necesitamos un número aleatorio dentro de un rango específico, podemos multiplicarlo por un valor específico y luego redondearlo.
Matemáticas.pow(a,b)
Calcule a b , por ejemplo:
console.log(Math.pow(2,3));//8
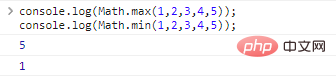
Matemáticas.max()/Math.min()
Elija un valor máximo/mínimo entre cualquier número de argumentos:
console.log(Math.max(1,2,3,4,5));//5console.log(Math.min(1,2,3,4,5));//1