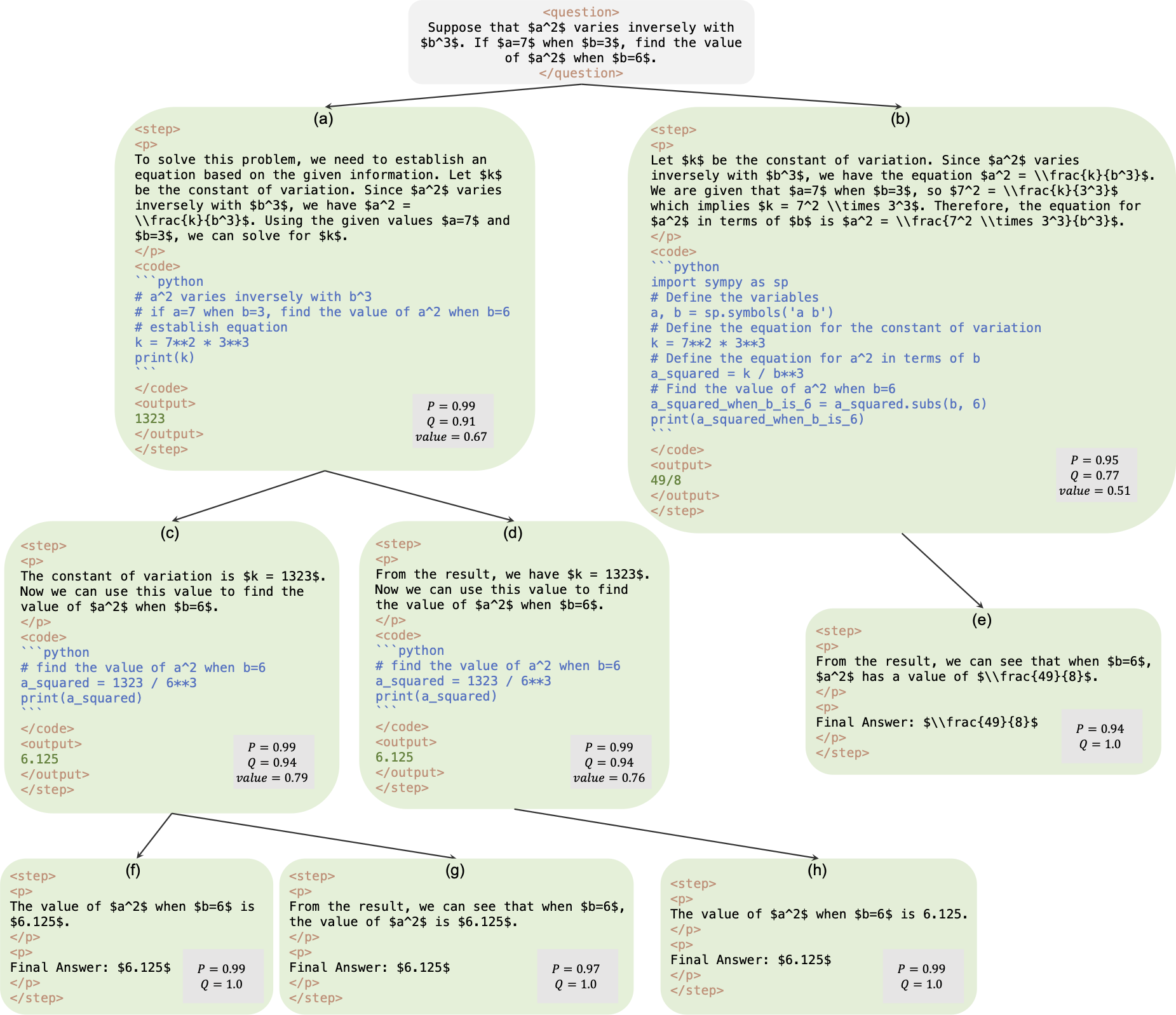
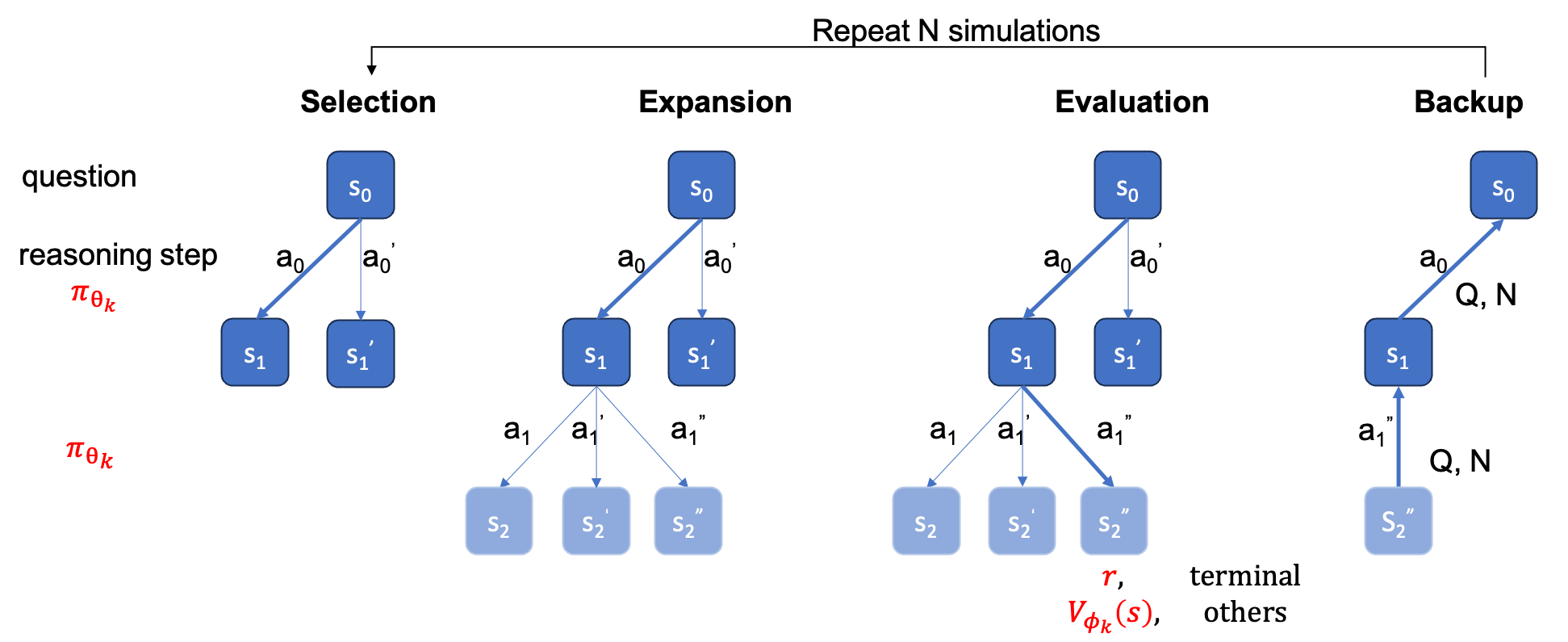
Ceci est le référentiel officiel du papier AlphaMath Almost Zero : supervision des processus sans processus. Le code est extrait de notre base de code interne d'entreprise. En conséquence, il peut y avoir de légères différences lors de la reproduction des chiffres rapportés dans notre article, mais ils devraient être très proches. Notre approche consiste à former les modèles de politique et de valeur en utilisant uniquement le raisonnement mathématique dérivé du cadre Monte Carlo Tree Search (MCTS), éliminant ainsi le besoin de GPT-4 ou d'annotations humaines. Ceci est une illustration de l'instance de formation générée par MCTS au tour 3.
Point de contrôle : AlphaMath-7B tour 3 ? / AlphaMath-7B tour 3 ?
Ensemble de données : AlphaMath-Round3-Trainset ? Le processus de résolution des données de formation est automatiquement généré sur la base du MCTS et du point de contrôle du deuxième tour. Des exemples positifs et négatifs sont inclus pour la formation des modèles de politique et de valeur.
Code de formation : en raison de la politique, nous ne pouvons publier que les détails d'implémentation de certaines fonctions clés, qui doivent essentiellement être modifiées dans votre propre code de formation.
| Méthode d'inférence | Précision | moy. temps (s) par q | moy. mesures | # sols |
|---|---|---|---|---|
| Cupide | 53.62 | 1.6 | 3.1 | 1 |
| Maj@5 | 61,84 | 2.9 | 2.9 | 5 |
| Poutre au niveau de l'étape (1,5) | 62.32 | 3.1 | 3.0 | top-1 |
| 5 courses + Maj@5 | 67.04 | x5 | x1 | 5 premiers-1 |
| Poutre au niveau de l'étape (2,5) | 64,66 | 2.4 | 2.4 | top-1 |
| Poutre au niveau de l'étape (3,5) | 65,74 | 2.3 | 2.2 | top-1 |
| Poutre au niveau de l'étape (5,5) | 65,98 | 4.7 | 2.3 | top-1 |
| 1 course + Maj@5 | 66,54 | x1 | x1 | top-5 |
| 5 courses + Maj@5 | 69,94 | x5 | x1 | 5 premiers-1 |
| SCTM (N=40) | 64.02 | 10.1 | 3.8 | top-1 |
+ Maj@5 nécessite de courir 5 fois, ce qui favorise la diversité.+ Maj@5 utilise directement les 5 candidats, ce qui manque de diversité.| température | 0,6 | 1.0 |
|---|---|---|
| Poutre au niveau de l'étape (1,5) | 62.32 | 62,76 |
| Poutre au niveau de l'étape (2,5) | 64,66 | 65,60 |
| Poutre au niveau de l'étape (3,5) | 65,74 | 66.28 |
| Poutre au niveau de l'étape (5,5) | 65,98 | 66.38 |
Pour une recherche de faisceau par étapes, le réglage de temperature=1.0 peut donner des résultats légèrement meilleurs.
requirements.txt pip install -r requirements.txt
Ou suivez simplement les cmds
> git clone https://github.com/MARIO-Math-Reasoning/Super_MARIO.git
> git clone https://github.com/MARIO-Math-Reasoning/MARIO_EVAL.git
> git clone https://github.com/MARIO-Math-Reasoning/vllm.git
> cd Super_MARIO && pip install -r requirements.txt && cd ..
> cd MARIO_EVAL/latex2sympy && pip install . && cd ..
> pip install -e .
> cd ../vllm
> pip install -e . scripts/save_value_head.py pour ajouter la valeur head au LLM. Vous pouvez exécuter l’une des deux commandes suivantes. Il peut y avoir une légère différence de précision entre les deux. Dans notre machine, le premier a obtenu 53,4 % et le second 53,62 %.
python react_batch_demo.py
--custom_cfg configs/react_sft.yaml
--qaf ../MARIO_EVAL/data/math_testset_annotation.json
ou
# use step_beam (1, 1) without value func
python solver_demo.py
--custom_cfg configs/sbs_greedy.yaml
--qaf ../MARIO_EVAL/data/math_testset_annotation.json
Dans notre machine, sur l'ensemble de tests MATH, la cmd suivante avec la configuration B1=1, B2=5 peut atteindre ~62 %, et celle avec la configuration B1=3, B2=5 peut atteindre ~65 %.
python solver_demo.py
--custom_cfg configs/sbs_sft.yaml
--qaf ../MARIO_EVAL/data/math_testset_annotation.json
Calculer la précision
python eval_output_jsonl.py
--res_file <the saved tree jsonl file by solver_demo.py>
La ground_truth (la réponse finale, pas le processus de solution) doit être fournie dans le fichier qaf json ou jsonl (un exemple de format peut faire référence à ../MARIO_EVAL/data/math_testset_annotation.json ).
tour 1
# Checkpoint Initialization is required by adding value head
python solver_demo.py
--custom_cfg configs/mcts_round1.yaml
--qaf /path/to/training/data
tour > 1, après SFT
python solver_demo.py
--custom_cfg configs/mcts_sft_round.yaml
--qaf /path/to/training/data
Seule question sera utilisée pour la génération de solutions, mais ground_truth sera utilisée pour calculer la précision.
python solver_demo.py
--custom_cfg configs/mcts_sft.yaml
--qaf ../MARIO_EVAL/data/math_testset_annotation.json
Contrairement à la recherche de faisceau par étapes, vous devez d'abord créer un arbre complet, puis exécuter le MCTS hors ligne, puis calculer la précision.
python offline_inference.py
--custom_cfg configs/offline_inference.yaml
--tree_jsonl <the saved tree jsonl file by solver_demo.py>
Remarque : ce script d'évaluation peut également être exécuté avec une recherche de faisceau au niveau de l'arborescence enregistrée par étape, et la précision doit rester la même.
Étant donné que la vérité terrain est connue pour les données d'entraînement, la valeur de l'étape finale est une récompense et la valeur Q peut très bien converger.
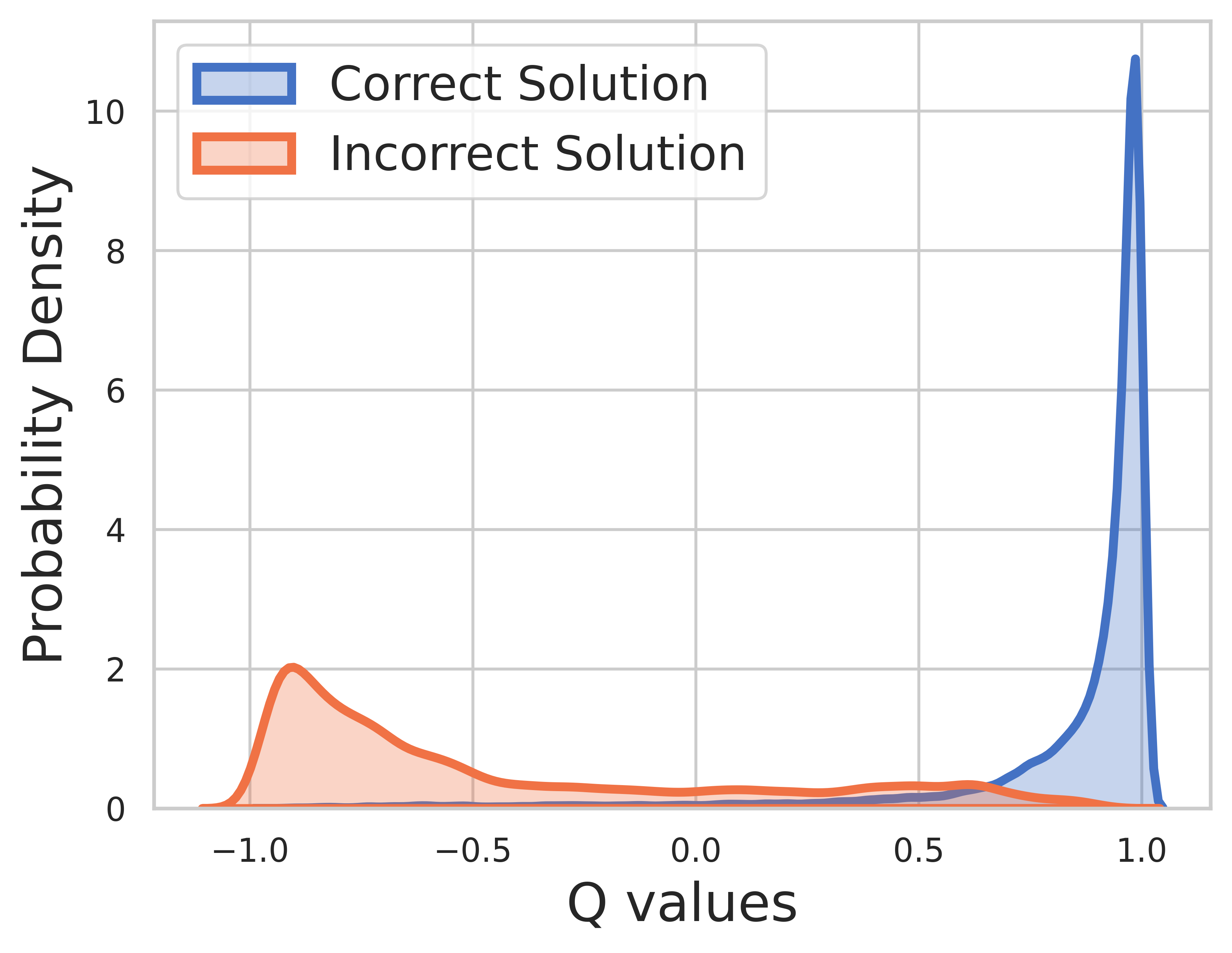
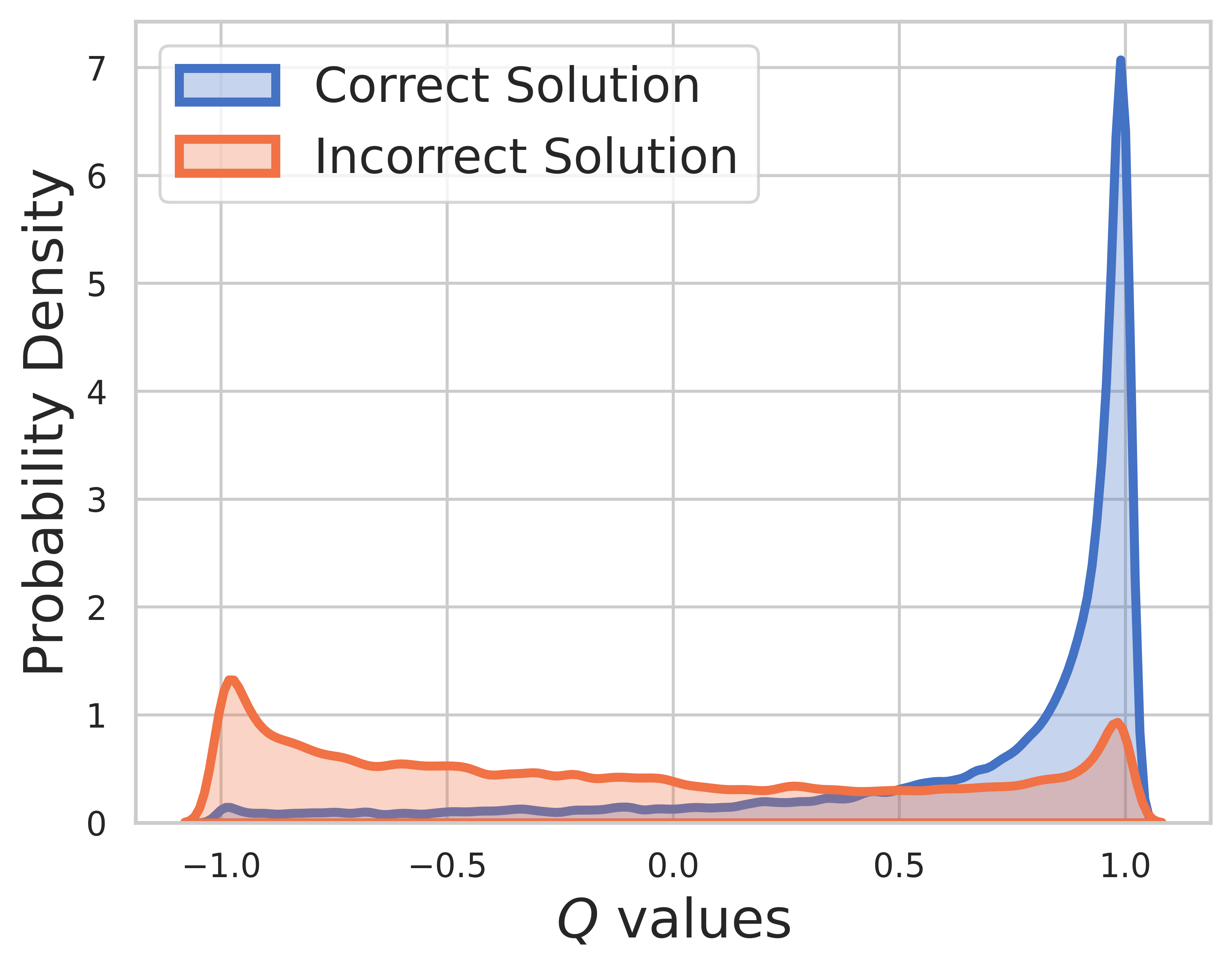
Sur l'ensemble de test, la vérité terrain est inconnue, donc la distribution de la valeur Q comprend à la fois des étapes intermédiaires et finales. A partir de cette figure, on peut trouver
SVPO par SCTM
@misc{chen2024steplevelvaluepreferenceoptimization,
title={Step-level Value Preference Optimization for Mathematical Reasoning},
author={Guoxin Chen and Minpeng Liao and Chengxi Li and Kai Fan},
year={2024},
eprint={2406.10858},
archivePrefix={arXiv},
primaryClass={cs.CL},
url={https://arxiv.org/abs/2406.10858},
}
Version SCTM
@misc{chen2024alphamathzeroprocesssupervision,
title={AlphaMath Almost Zero: process Supervision without process},
author={Guoxin Chen and Minpeng Liao and Chengxi Li and Kai Fan},
year={2024},
eprint={2405.03553},
archivePrefix={arXiv},
primaryClass={cs.CL},
url={https://arxiv.org/abs/2405.03553},
}
Boîte à outils d'évaluation
@misc{zhang2024marioevalevaluatemath,
title={MARIO Eval: Evaluate Your Math LLM with your Math LLM--A mathematical dataset evaluation toolkit},
author={Boning Zhang and Chengxi Li and Kai Fan},
year={2024},
eprint={2404.13925},
archivePrefix={arXiv},
primaryClass={cs.CL},
url={https://arxiv.org/abs/2404.13925},
}
Version OVM (modèle de valeur de résultat)
@misc{liao2024mariomathreasoningcode,
title={MARIO: MAth Reasoning with code Interpreter Output -- A Reproducible Pipeline},
author={Minpeng Liao and Wei Luo and Chengxi Li and Jing Wu and Kai Fan},
year={2024},
eprint={2401.08190},
archivePrefix={arXiv},
primaryClass={cs.CL},
url={https://arxiv.org/abs/2401.08190},
}