Le rééchantillonnage Lanczos (prononcé Lanchos) est une technique sophistiquée d'interpolation de signaux numériques, offrant une qualité d'image supérieure par rapport aux méthodes plus simples comme le plus proche voisin et l'interpolation bilinéaire. En préservant efficacement les détails et en minimisant les artefacts d'alias, le rééchantillonnage de Lanczos est largement utilisé dans les applications de traitement d'image et de signal.
Bien que Lanczos excelle dans la qualité d’image, cela se fait au prix d’une complexité informatique accrue. De plus, le risque d'artefacts de « sonnerie », en particulier autour des arêtes vives, peut constituer un inconvénient. Malgré ces défis, Lanczos reste un choix privilégié pour des tâches telles que la mise à l'échelle et la rotation d'images en raison de ses avantages globaux en termes de performances.
Ce document fournit un aperçu complet du rééchantillonnage Lanczos, y compris ses fondements théoriques, les détails de mise en œuvre et les applications pratiques. Il constitue une ressource précieuse pour les développeurs et les chercheurs cherchant à comprendre et à utiliser cette technique puissante. Les sections suivantes approfondissent les aspects cruciaux du rééchantillonnage de Lanczos, tels que le noyau de Lanczos, les processus d'interpolation et de rééchantillonnage, la préservation du flux, le suréchantillonnage, le sous-échantillonnage, le positionnement de l'échantillon, la plage de sortie, l'interpolation multidimensionnelle et la séparabilité. Un exemple pratique accompagné du code source est inclus.
Le noyau Lanczos, défini pour une taille de support donnée, est une fonction utilisée dans le rééchantillonnage Lanczos. Le noyau est défini comme :
L(x) = sinc(x)*sinc(x/a) : -a < x < a
= 0.0 : otherwise
Où:
La fonction sinc normalisée est définie comme :
sinc(x) = 1.0 : x = 0.0
= sin(PI*x)/(PI*x) : otherwise
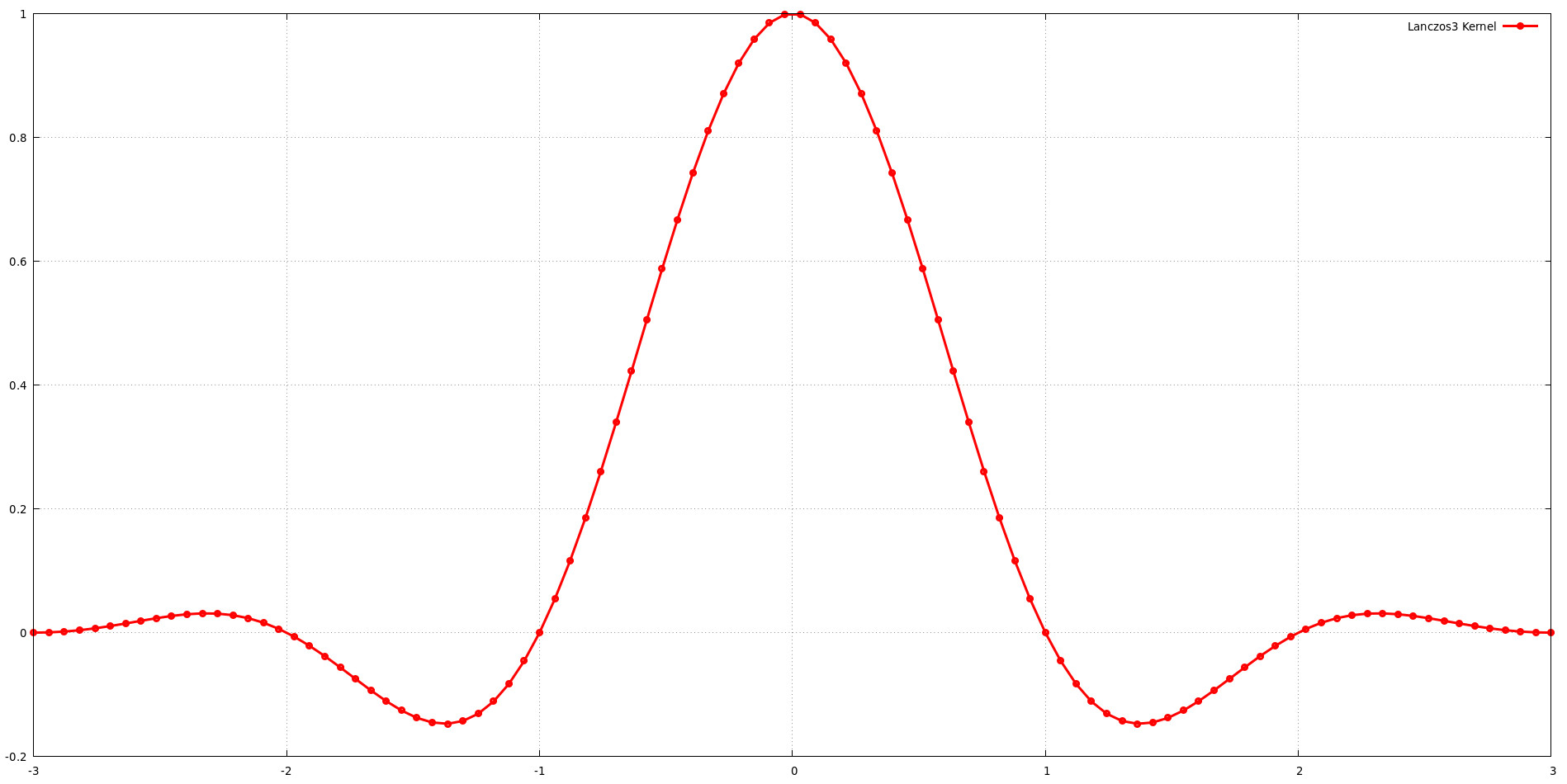
Le graphique illustre la forme du noyau de Lanczos pour une taille de support de a = 3. Cela signifie que le noyau comprend trois lobes de la fonction sinc. Bien que l'augmentation de la taille du support (a) offre généralement plus de flexibilité pour façonner la réponse en fréquence, elle augmente également le coût de calcul. Un équilibre doit être trouvé entre la qualité de l’image et l’efficacité informatique lors du choix de la taille du support. La découverte de Jim Blinn selon laquelle le noyau Lanczos avec a = 3 offre un excellent équilibre entre préservation des basses fréquences et rejet des hautes fréquences conforte cette notion.
Remarque : Les termes « largeur du noyau », « taille du support » et « taille du filtre » sont souvent utilisés de manière interchangeable pour décrire le paramètre a. Cependant, dans le contexte du rééchantillonnage de Lanczos, la « taille du support » reflète le plus fidèlement le concept.
L'interpolation Lanczos est une technique utilisée pour rééchantillonner un signal discret à une nouvelle fréquence d'échantillonnage. Il y parvient en convoluant le signal original avec un noyau Lanczos.
Le signal interpolé s2(x) peut être calculé comme suit :
s2(x) = (1/w(x))*
SUM(i = -a + 1, i = a,
s1(floor(x) + i)*
L(i - x + floor(x)))
Où:
Préserver le flux :
Le facteur de normalisation w(x) est crucial pour préserver l’énergie ou la masse globale du signal pendant le processus d’interpolation. Cela garantit que la somme des valeurs interpolées se rapproche de la somme des échantillons originaux. Le poids du filtre est calculé comme suit :
w(x) = SUM(i = -a + 1, i = a, L(i - x + floor(x)))
Suréchantillonnage :
Lors de l'augmentation du taux d'échantillonnage, l'équation d'interpolation de Lanczos peut être utilisée directement sans modifications.
Sous-échantillonnage :
Pour éviter les artefacts d'alias lors de la diminution du taux d'échantillonnage, l'échelle du filtre doit être ajustée pour correspondre au nouveau taux d'échantillonnage.
fs = n1/n2
s2(x) = (1/w(x))*
SUM(i = -(fs*a) + 1, i = (fs*a),
s1(floor(x) + i)*
L((i - x + floor(x))/fs))
Où:
Lors du rééchantillonnage d'un signal de n1 échantillons à n2 échantillons, les positions d'échantillon suivantes sont utilisées. L'indice j est utilisé pour représenter les échantillons du signal échantillonné s2(x). Le terme (j + 0,5) est le centre d'un échantillon dans s2(x). L’étape met à l’échelle un point de s2(x) en un point de s1(x). Le terme final -0,5 dans x est un déphasage qui provoque le décalage des échantillons du coefficient de Lanczos.
step = n1/n2
j = [0..n2)
x = (j + 0.5)*step - 0.5
Lors de l'interpolation Lanczos, une attention particulière doit être apportée aux limites du signal. Les techniques courantes de manipulation des bords comprennent :
Remplissage zéro :
s1(x) = s1[floor(x)] : x = [0, n1)
= 0.0 : otherwise
Serrage :
s1(x) = s1[clamp(floor(x), 0, n1 - 1)]
Le serrage est souvent préféré car il réduit les artefacts de bord causés par des discontinuités marquées près des bords. Cependant, le choix de la méthode de traitement des bords dépend de l'application spécifique et du résultat souhaité.
La plage de s2(x) peut être supérieure à celle de s1(x) en raison des lobes de L(x). Par exemple, un signal d'entrée s1(x) correspondant aux couleurs de pixels dans la plage de [0,0,1,0] doit être limité à la même plage pour garantir que les valeurs de sortie ne débordent pas lorsqu'elles sont reconverties en octets non signés de [0,255] .
Le noyau Lanczos peut être étendu à plusieurs dimensions pour effectuer une interpolation sur des images ou des données de dimension supérieure.
Le noyau de Lanczos bidimensionnel est défini comme :
L(x, y) = sinc(sqrt(x^2 + y^2))*sinc(sqrt(x^2 + y^2)/a)
Le signal interpolé s2(x, y) peut être calculé à l'aide de la formule suivante :
s2(x, y) = (1/w(x, y))*
SUM(i = -a + 1, i = a,
SUM(j = -a + 1, j = a,
s1(floor(x) + j, floor(y) + i)*
L(j - x + floor(x), i - y + floor(y))))
Où w(x, y) est le facteur de normalisation calculé à l'aide du noyau de Lanczos bidimensionnel.
Contrairement à certaines méthodes d'interpolation, le noyau de Lanczos est non séparable, ce qui signifie qu'il ne peut pas être pris en compte dans le produit de noyaux unidimensionnels. Cette propriété entraîne généralement des coûts de calcul plus élevés par rapport aux noyaux séparables. Pour améliorer les performances, certaines implémentations se rapprochent du noyau Lanczos en effectuant des passes séparées pour les dimensions horizontales et verticales.
Interpolation horizontale :
Interpolation verticale :
Représentation mathématique :
s2(x, y) = (1/w(x))*
SUM(j = -a + 1, j = a,
s1(floor(x) + j, y)*
L(j - x + floor(x)))
s3(x, y) = (1/w(y))*
SUM(i = -a + 1, i = a,
s2(x, floor(y) + i)*
L(i - y + floor(y)))
Notez que les facteurs de normalisation w(x) et w(y) sont calculés à l'aide du noyau de Lanczos unidimensionnel.
Points clés :
De même, le rééchantillonnage récursif d'un signal plusieurs fois, comme cela est couramment fait pour générer des mipmaps de texture, peut également dégrader la qualité de l'image en raison de l'accumulation d'erreurs à chaque étape de rééchantillonnage.
Exécutez l'exemple lancos-test et utilisez gnuplot pour voir comment le rééchantillonnage de Lanczos affecte un signal unidimensionnel simple lorsqu'il est suréchantillonné et sous-échantillonné d'un facteur 2.
make
./lanczos-test
gnuplot
> load "output.plot"
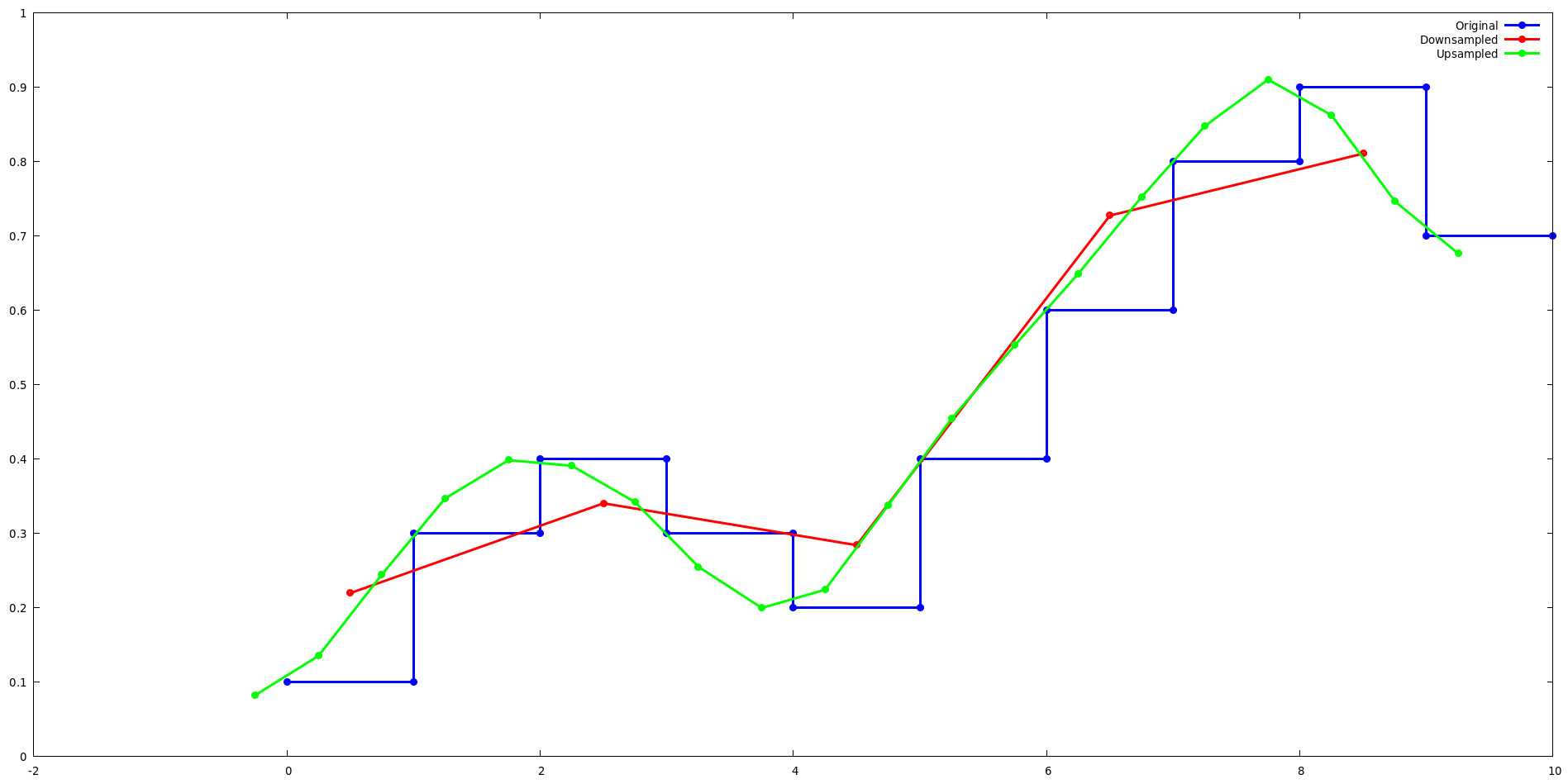
Suréchantillonnage :
Lors du suréchantillonnage par puissance de deux, le noyau Lanczos alterne entre des ensembles de valeurs de 2 niveaux. Par exemple, considérons les 4 premières sorties de l'exemple de suréchantillonnage lanzcos-test. Notez que les sorties pour L(x) se répètent pour j={0,2} et j={1,3}.
upsample n1=10, n2=20
j=0, x=-0.250000
i=-2, L(-2.750000)=0.007356, S1(-3.000000)=0.100000
i=-1, L(-1.750000)=-0.067791, S1(-2.000000)=0.100000
i=0, L(-0.750000)=0.270190, S1(-1.000000)=0.100000
i=1, L(0.250000)=0.890067, S1(0.000000)=0.100000
i=2, L(1.250000)=-0.132871, S1(1.000000)=0.300000
i=3, L(2.250000)=0.030021, S1(2.000000)=0.400000
s2=0.082129, s2/w=0.082379, w=0.996972
j=1, x=0.250000
i=-2, L(-2.250000)=0.030021, S1(-2.000000)=0.100000
i=-1, L(-1.250000)=-0.132871, S1(-1.000000)=0.100000
i=0, L(-0.250000)=0.890067, S1(0.000000)=0.100000
i=1, L(0.750000)=0.270190, S1(1.000000)=0.300000
i=2, L(1.750000)=-0.067791, S1(2.000000)=0.400000
i=3, L(2.750000)=0.007356, S1(3.000000)=0.300000
s2=0.134869, s2/w=0.135279, w=0.996972
j=2, x=0.750000
i=-2, L(-2.750000)=0.007356, S1(-2.000000)=0.100000
i=-1, L(-1.750000)=-0.067791, S1(-1.000000)=0.100000
i=0, L(-0.750000)=0.270190, S1(0.000000)=0.100000
i=1, L(0.250000)=0.890067, S1(1.000000)=0.300000
i=2, L(1.250000)=-0.132871, S1(2.000000)=0.400000
i=3, L(2.250000)=0.030021, S1(3.000000)=0.300000
s2=0.243853, s2/w=0.244594, w=0.996972
j=3, x=1.250000
i=-2, L(-2.250000)=0.030021, S1(-1.000000)=0.100000
i=-1, L(-1.250000)=-0.132871, S1(0.000000)=0.100000
i=0, L(-0.250000)=0.890067, S1(1.000000)=0.300000
i=1, L(0.750000)=0.270190, S1(2.000000)=0.400000
i=2, L(1.750000)=-0.067791, S1(3.000000)=0.300000
i=3, L(2.750000)=0.007356, S1(4.000000)=0.200000
s2=0.345945, s2/w=0.346996, w=0.996972
Sous-échantillonnage :
Lors d'un sous-échantillonnage par une puissance de deux, le noyau de Lanczos devient indépendant de x puisque (x - floor(x)) devient une constante qui correspond au déphasage. Par exemple, considérons les 2 premières sorties de l'exemple de sous-échantillonnage de lanzcos-test. Notez que les sorties de L(x) se répètent pour chaque j.
downsample n1=10, n2=5
j=0, x=0.500000
i=-5, L(-2.750000)=0.007356, S1(-5.000000)=0.100000
i=-4, L(-2.250000)=0.030021, S1(-4.000000)=0.100000
i=-3, L(-1.750000)=-0.067791, S1(-3.000000)=0.100000
i=-2, L(-1.250000)=-0.132871, S1(-2.000000)=0.100000
i=-1, L(-0.750000)=0.270190, S1(-1.000000)=0.100000
i=0, L(-0.250000)=0.890067, S1(0.000000)=0.100000
i=1, L(0.250000)=0.890067, S1(1.000000)=0.300000
i=2, L(0.750000)=0.270190, S1(2.000000)=0.400000
i=3, L(1.250000)=-0.132871, S1(3.000000)=0.300000
i=4, L(1.750000)=-0.067791, S1(4.000000)=0.200000
i=5, L(2.250000)=0.030021, S1(5.000000)=0.400000
i=6, L(2.750000)=0.007356, S1(6.000000)=0.600000
s2=0.437796, s2/w=0.219563, w=1.993943
j=1, x=2.500000
i=-5, L(-2.750000)=0.007356, S1(-3.000000)=0.100000
i=-4, L(-2.250000)=0.030021, S1(-2.000000)=0.100000
i=-3, L(-1.750000)=-0.067791, S1(-1.000000)=0.100000
i=-2, L(-1.250000)=-0.132871, S1(0.000000)=0.100000
i=-1, L(-0.750000)=0.270190, S1(1.000000)=0.300000
i=0, L(-0.250000)=0.890067, S1(2.000000)=0.400000
i=1, L(0.250000)=0.890067, S1(3.000000)=0.300000
i=2, L(0.750000)=0.270190, S1(4.000000)=0.200000
i=3, L(1.250000)=-0.132871, S1(5.000000)=0.400000
i=4, L(1.750000)=-0.067791, S1(6.000000)=0.600000
i=5, L(2.250000)=0.030021, S1(7.000000)=0.800000
i=6, L(2.750000)=0.007356, S1(8.000000)=0.900000
s2=0.678627, s2/w=0.340344, w=1.993943
À titre d'optimisation supplémentaire, le noyau de Lanczos peut être précalculé pour ces cas afin d'éliminer le calcul coûteux de la fonction sinc.
Ce README a été créé avec l'aide de Google Gemini.
Les références supplémentaires incluent :
Ce code a été implémenté par Jeff Boody sous la licence MIT.
Copyright (c) 2024 Jeff Boody
Permission is hereby granted, free of charge, to any person obtaining a
copy of this software and associated documentation files (the "Software"),
to deal in the Software without restriction, including without limitation
the rights to use, copy, modify, merge, publish, distribute, sublicense,
and/or sell copies of the Software, and to permit persons to whom the
Software is furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included
in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN
THE SOFTWARE.