Greedy Gaussian Segmentation (GGS) est un solveur Python permettant de segmenter efficacement les données de séries chronologiques multivariées. Pour les détails de mise en œuvre, veuillez consulter notre article sur http://stanford.edu/~boyd/papers/ggs.html.
Le Solveur GGS prend une matrice de données n par T et divise les horodatages T sur un vecteur à n dimensions en segments sur lesquels les données sont bien expliquées sous forme d'échantillons indépendants à partir d'une distribution gaussienne multivariée. Pour ce faire, il formule un problème de maximum de vraisemblance régularisé par covariance et le résout à l'aide d'une heuristique gloutonne, avec tous les détails décrits dans l'article.
git clone [email protected]:davidhallac/GGS.git
cd GGS
python helloworld.py
ggs.py se trouve dans le même répertoire que votre nouveau fichier, puis ajoutez le code suivant au début de votre script : from ggs import *
Le package GGS a trois fonctions principales :
bps, objectives = GGS(data, Kmax, lamb)
Trouve K points d'arrêt dans les données pour un paramètre de régularisation lambda donné
Entrées
data - une matrice de données n par T, avec T horodatages d'un vecteur à n dimensions
Kmax - le nombre de points d'arrêt à trouver
lamb - paramètre de régularisation pour la covariance régularisée
Retours
bps - Liste de listes, où l'élément i de la plus grande liste est l'ensemble des points d'arrêt trouvés à K = i dans l'algorithme GGS
objectifs - Liste des valeurs objectives à chaque étape intermédiaire (pour K = 0 à Kmax)
meancovs = GGSMeanCov(data, breakpoints, lamb)
Recherche les moyennes et les covariances régularisées de chaque segment, étant donné un ensemble de points d'arrêt.
Entrées
data - une matrice de données n par T, avec T horodatages d'un vecteur à n dimensions
points d'arrêt - une liste d'emplacements de points d'arrêt
lamb - paramètre de régularisation pour la covariance régularisée
Retours
Meancovs - une liste de tuples (moyenne, covariance) pour chaque segment des données
cvResults = GGSCrossVal(data, Kmax=25, lambList = [0.1, 1, 10])
Exécute une validation croisée 10 fois et renvoie la probabilité d'entraînement et d'ensemble de test pour chaque paire (K, lambda) jusqu'à Kmax
Entrées
data - une matrice de données n par T, avec T horodatages d'un vecteur à n dimensions
Kmax - le nombre maximum de points d'arrêt sur lesquels exécuter GGS
lambList - une liste de paramètres de régularisation à tester
Retours
cvResults - liste de tuples (lamb, ([TrainLL],[TestLL])) pour chaque paramètre de régularisation dans lambList. Ici, TrainLL et TestLL représentent la vraisemblance moyenne par échantillon sur les 10 niveaux de validation croisée pour tous les K de 0 à Kmax.
Paramètres facultatifs supplémentaires (pour les trois fonctions ci-dessus) :
Features = [] - sélectionnez un certain sous-ensemble de colonnes dans les données sur lesquelles opérer
verbose = False - Imprimer les étapes intermédiaires lors de l'exécution de l'algorithme
L'exécution financeExample.py donnera le tracé suivant, montrant l'objectif (équation 4 dans l'article) par rapport au nombre de points d'arrêt :
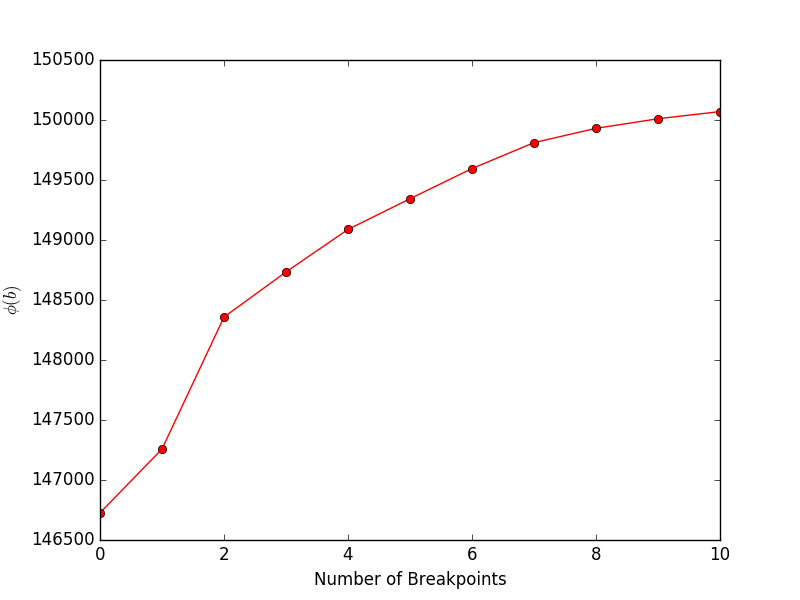
Une fois que nous avons résolu les emplacements des points d'arrêt, nous pouvons utiliser la fonction FindMeanCovs() pour trouver les moyennes et les covariances de chaque segment. Dans l'exemple de helloworld.py , tracer les moyennes, les variances et les covariances des trois signaux donne :
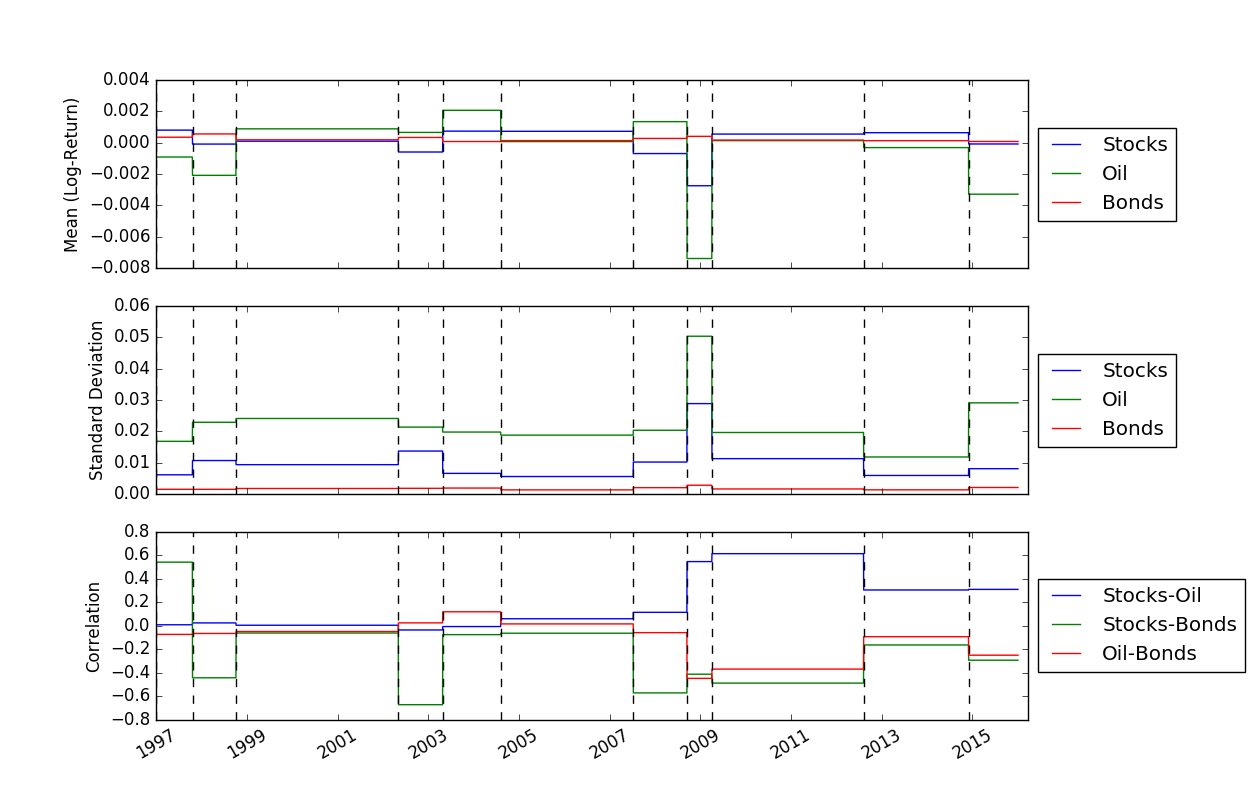
Pour exécuter une validation croisée, qui peut être utile pour déterminer les valeurs optimales de K et lambda, nous pouvons utiliser le code suivant pour charger les données, exécuter la validation croisée, puis tracer le test et entraîner la probabilité :
from ggs import *
import numpy as np
import matplotlib.pyplot as plt
filename = "Returns.txt"
data = np.genfromtxt(filename,delimiter=' ')
feats = [0,3,7]
#Run cross-validaton up to Kmax = 30, at lambda = 1e-4
maxBreaks = 30
lls = GGSCrossVal(data, Kmax=maxBreaks, lambList = [1e-4], features = feats, verbose = False)
trainLikelihood = lls[0][1][0]
testLikelihood = lls[0][1][1]
plt.plot(range(maxBreaks+1), testLikelihood)
plt.plot(range(maxBreaks+1), trainLikelihood)
plt.legend(['Test LL','Train LL'], loc='best')
plt.show()
Le tracé résultant ressemble à :
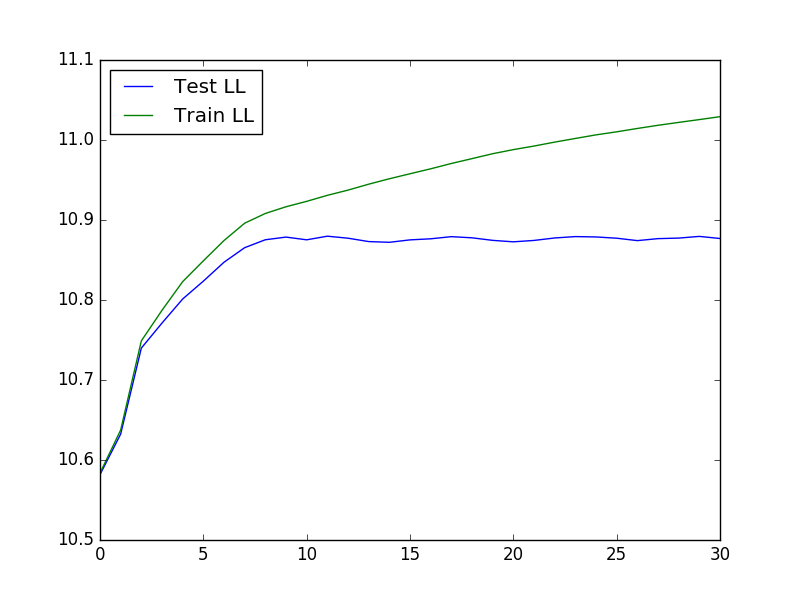
Segmentation gaussienne gourmande de données de séries chronologiques - D. Hallac, P. Nystrup et S. Boyd
David Hallac, Peter Nystrup et Stephen Boyd.