dans ce fichier, j'ai implémenté llama3 à partir de zéro, une multiplication tensorielle et matricielle à la fois.
De plus, je vais charger des tenseurs directement à partir du fichier de modèle fourni par Meta pour Llama3, vous devez télécharger les poids avant d'exécuter ce fichier. voici le lien officiel pour télécharger les poids : https://llama.meta.com/llama-downloads/
je ne vais pas implémenter de tokenizer bpe (mais Andrej Karpathy a une implémentation vraiment propre)
lien vers son implémentation : https://github.com/karpathy/minbpe
from pathlib import Path
import tiktoken
from tiktoken . load import load_tiktoken_bpe
import torch
import json
import matplotlib . pyplot as plt
tokenizer_path = "Meta-Llama-3-8B/tokenizer.model"
special_tokens = [
"<|begin_of_text|>" ,
"<|end_of_text|>" ,
"<|reserved_special_token_0|>" ,
"<|reserved_special_token_1|>" ,
"<|reserved_special_token_2|>" ,
"<|reserved_special_token_3|>" ,
"<|start_header_id|>" ,
"<|end_header_id|>" ,
"<|reserved_special_token_4|>" ,
"<|eot_id|>" , # end of turn
] + [ f"<|reserved_special_token_ { i } |>" for i in range ( 5 , 256 - 5 )]
mergeable_ranks = load_tiktoken_bpe ( tokenizer_path )
tokenizer = tiktoken . Encoding (
name = Path ( tokenizer_path ). name ,
pat_str = r"(?i:'s|'t|'re|'ve|'m|'ll|'d)|[^rnp{L}p{N}]?p{L}+|p{N}{1,3}| ?[^sp{L}p{N}]+[rn]*|s*[rn]+|s+(?!S)|s+" ,
mergeable_ranks = mergeable_ranks ,
special_tokens = { token : len ( mergeable_ranks ) + i for i , token in enumerate ( special_tokens )},
)
tokenizer . decode ( tokenizer . encode ( "hello world!" )) 'hello world!'
normalement, la lecture de ceci dépend de la façon dont les classes de modèles sont écrites et des noms de variables qu'elles contiennent.
mais comme nous implémentons llama3 à partir de zéro, nous lirons le fichier un tenseur à la fois.
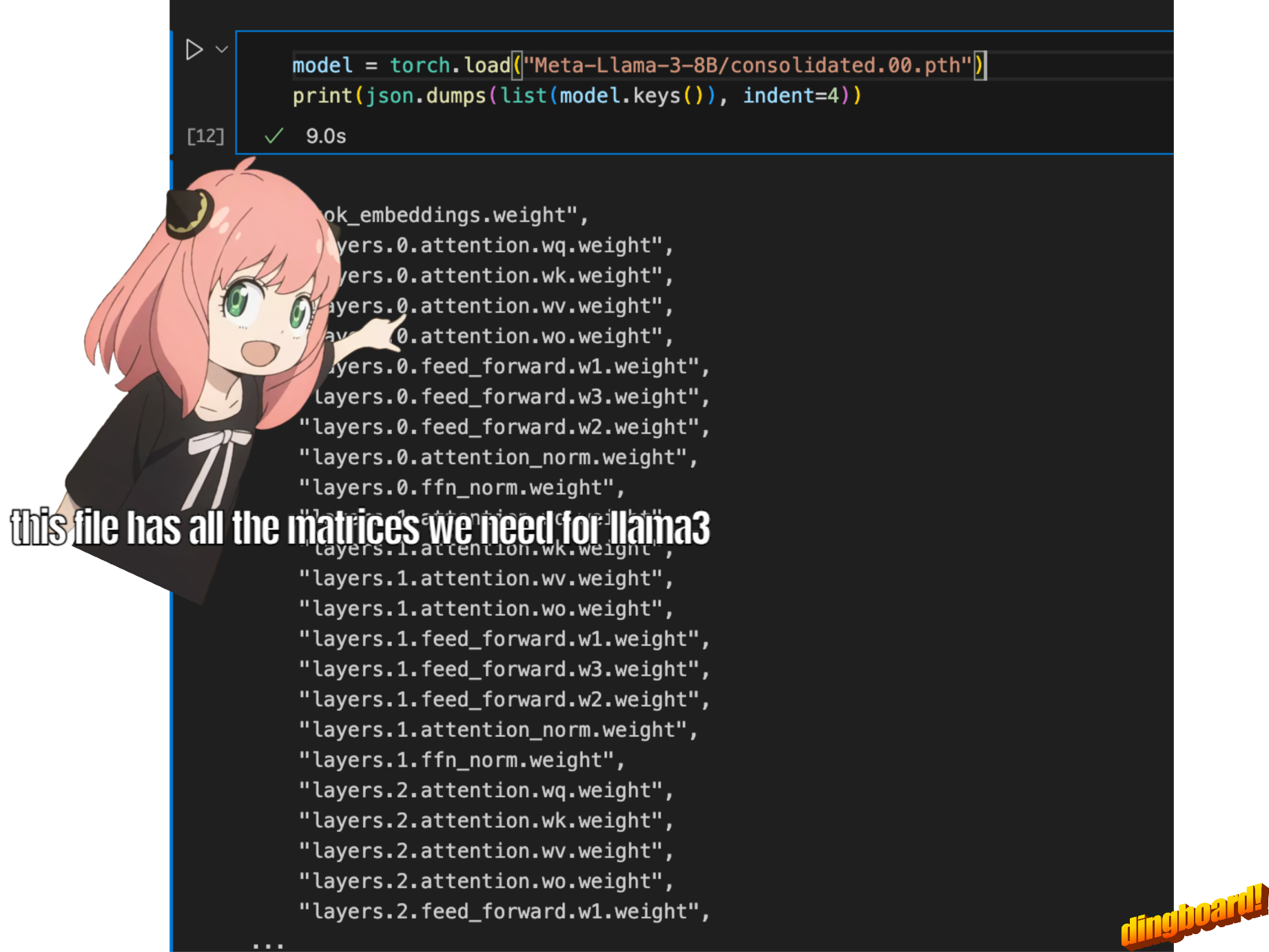
model = torch . load ( "Meta-Llama-3-8B/consolidated.00.pth" )
print ( json . dumps ( list ( model . keys ())[: 20 ], indent = 4 )) [
"tok_embeddings.weight",
"layers.0.attention.wq.weight",
"layers.0.attention.wk.weight",
"layers.0.attention.wv.weight",
"layers.0.attention.wo.weight",
"layers.0.feed_forward.w1.weight",
"layers.0.feed_forward.w3.weight",
"layers.0.feed_forward.w2.weight",
"layers.0.attention_norm.weight",
"layers.0.ffn_norm.weight",
"layers.1.attention.wq.weight",
"layers.1.attention.wk.weight",
"layers.1.attention.wv.weight",
"layers.1.attention.wo.weight",
"layers.1.feed_forward.w1.weight",
"layers.1.feed_forward.w3.weight",
"layers.1.feed_forward.w2.weight",
"layers.1.attention_norm.weight",
"layers.1.ffn_norm.weight",
"layers.2.attention.wq.weight"
]
with open ( "Meta-Llama-3-8B/params.json" , "r" ) as f :
config = json . load ( f )
config {'dim': 4096,
'n_layers': 32,
'n_heads': 32,
'n_kv_heads': 8,
'vocab_size': 128256,
'multiple_of': 1024,
'ffn_dim_multiplier': 1.3,
'norm_eps': 1e-05,
'rope_theta': 500000.0}
dim = config [ "dim" ]
n_layers = config [ "n_layers" ]
n_heads = config [ "n_heads" ]
n_kv_heads = config [ "n_kv_heads" ]
vocab_size = config [ "vocab_size" ]
multiple_of = config [ "multiple_of" ]
ffn_dim_multiplier = config [ "ffn_dim_multiplier" ]
norm_eps = config [ "norm_eps" ]
rope_theta = torch . tensor ( config [ "rope_theta" ])ici, nous utilisons tiktoken (je pense une bibliothèque openai) comme tokenizer
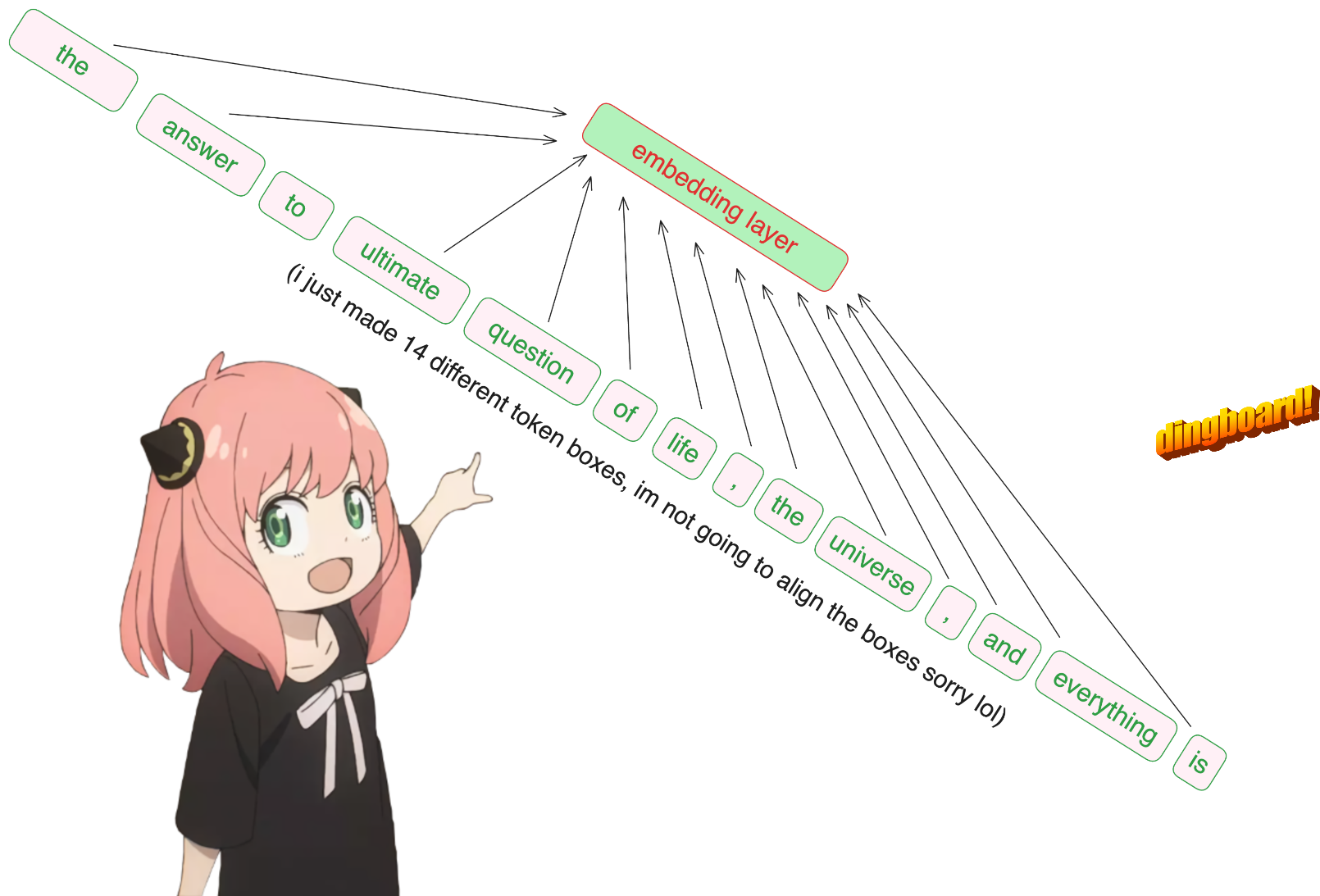
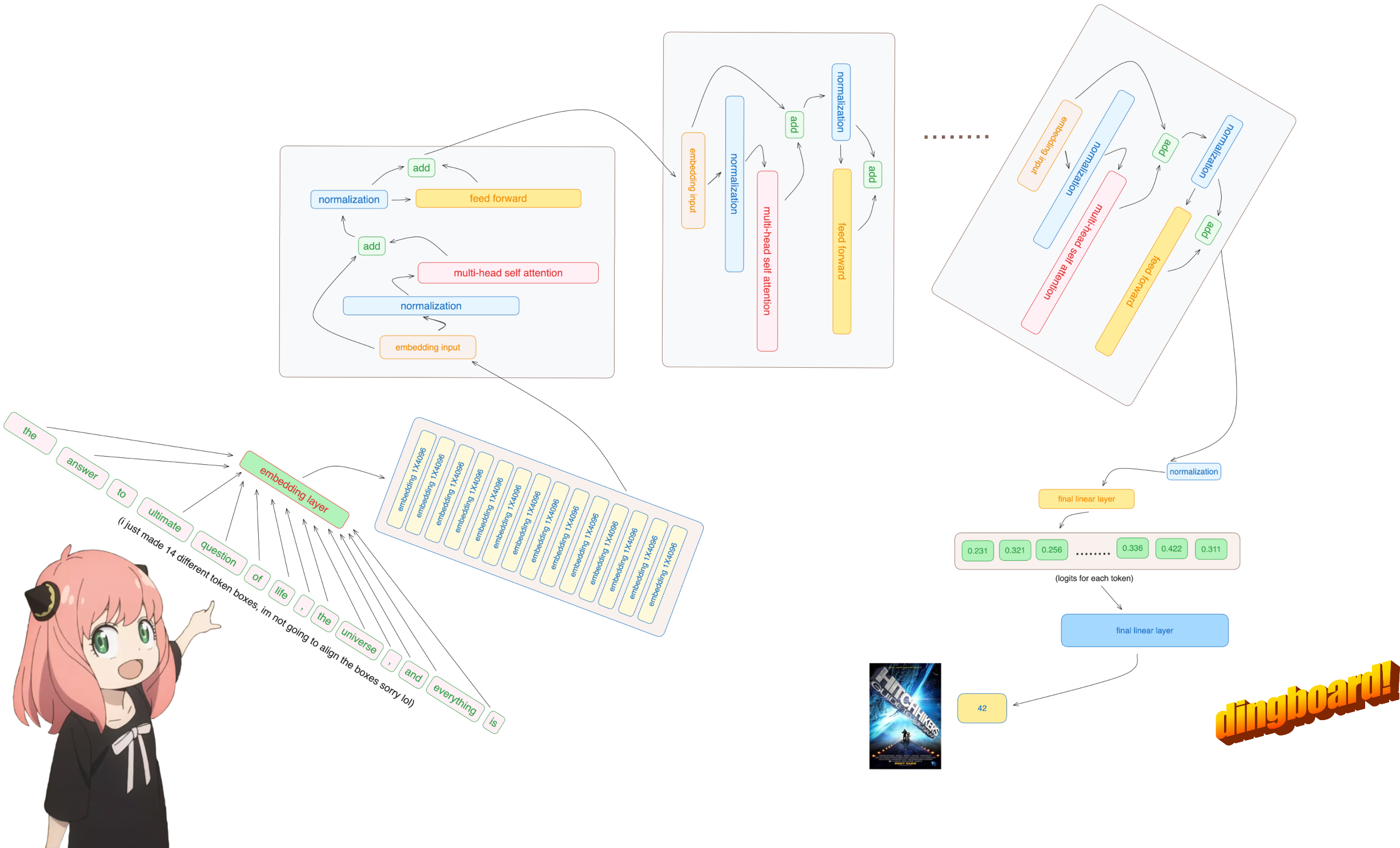
prompt = "the answer to the ultimate question of life, the universe, and everything is "
tokens = [ 128000 ] + tokenizer . encode ( prompt )
print ( tokens )
tokens = torch . tensor ( tokens )
prompt_split_as_tokens = [ tokenizer . decode ([ token . item ()]) for token in tokens ]
print ( prompt_split_as_tokens ) [128000, 1820, 4320, 311, 279, 17139, 3488, 315, 2324, 11, 279, 15861, 11, 323, 4395, 374, 220]
['<|begin_of_text|>', 'the', ' answer', ' to', ' the', ' ultimate', ' question', ' of', ' life', ',', ' the', ' universe', ',', ' and', ' everything', ' is', ' ']
Je suis désolé mais c'est la seule partie de la base de code où j'utilise un module de réseau neuronal intégré
de toute façon, donc nos jetons [17x1] sont maintenant [17x4096], soit 17 intégrations (une pour chaque jeton) de longueur 4096
note : gardez une trace des formes, cela permet de tout comprendre beaucoup plus facilement

embedding_layer = torch . nn . Embedding ( vocab_size , dim )
embedding_layer . weight . data . copy_ ( model [ "tok_embeddings.weight" ])
token_embeddings_unnormalized = embedding_layer ( tokens ). to ( torch . bfloat16 )
token_embeddings_unnormalized . shape torch.Size([17, 4096])
s'il vous plaît, notez qu'après cette étape, les formes ne changent pas, les valeurs sont simplement normalisées
choses à garder à l'esprit, nous avons besoin d'un norm_eps (de la configuration) car nous ne voulons pas définir accidentellement rms sur 0 et diviser par 0
voici la formule :

# def rms_norm(tensor, norm_weights):
# rms = (tensor.pow(2).mean(-1, keepdim=True) + norm_eps)**0.5
# return tensor * (norm_weights / rms)
def rms_norm ( tensor , norm_weights ):
return ( tensor * torch . rsqrt ( tensor . pow ( 2 ). mean ( - 1 , keepdim = True ) + norm_eps )) * norm_weights vous me verrez accéder à layer.0 à partir du modèle dict (c'est la première couche)
de toute façon, donc après avoir normalisé nos formes sont toujours [17x4096] identiques à l'intégration mais normalisées
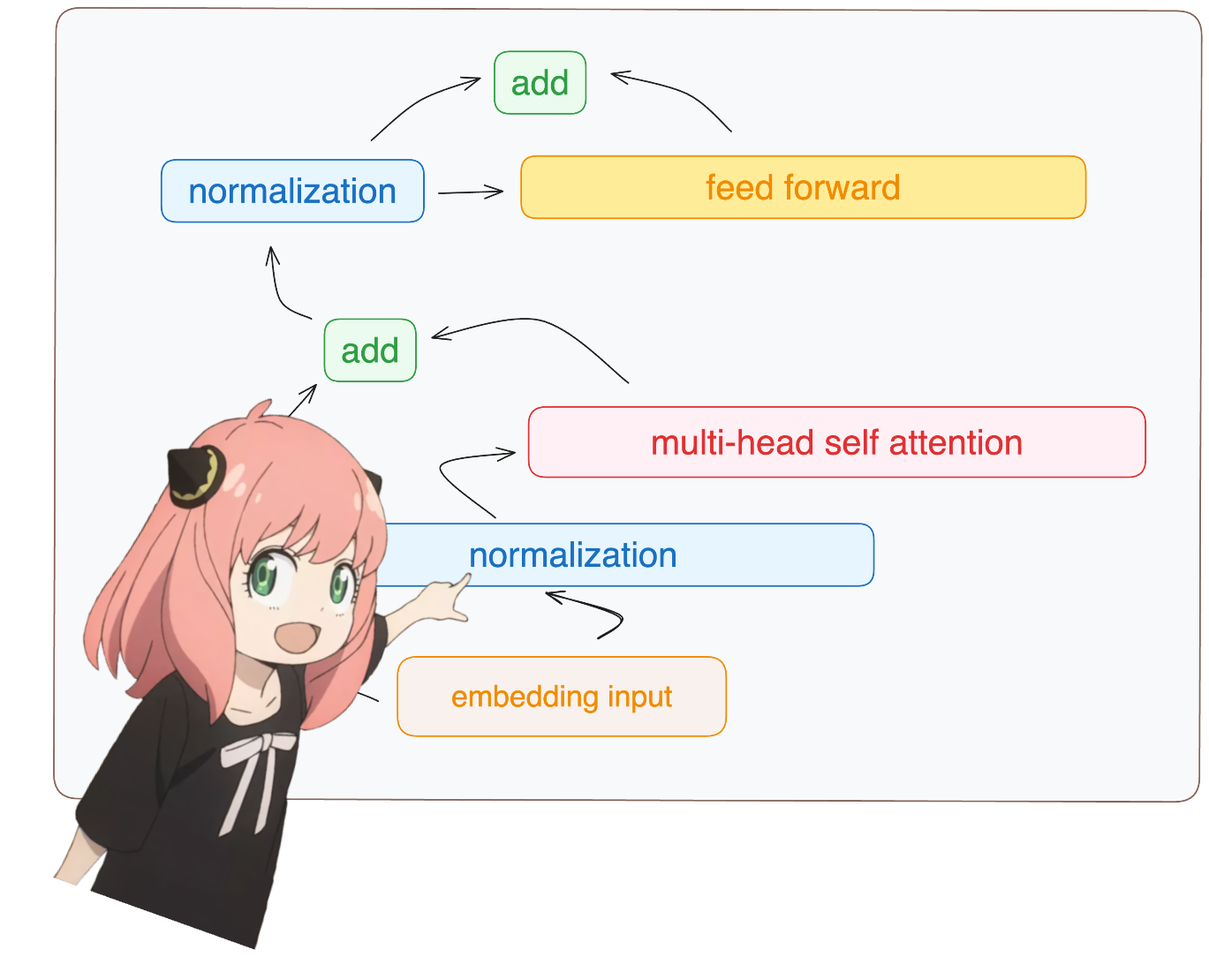
token_embeddings = rms_norm ( token_embeddings_unnormalized , model [ "layers.0.attention_norm.weight" ])
token_embeddings . shape torch.Size([17, 4096])
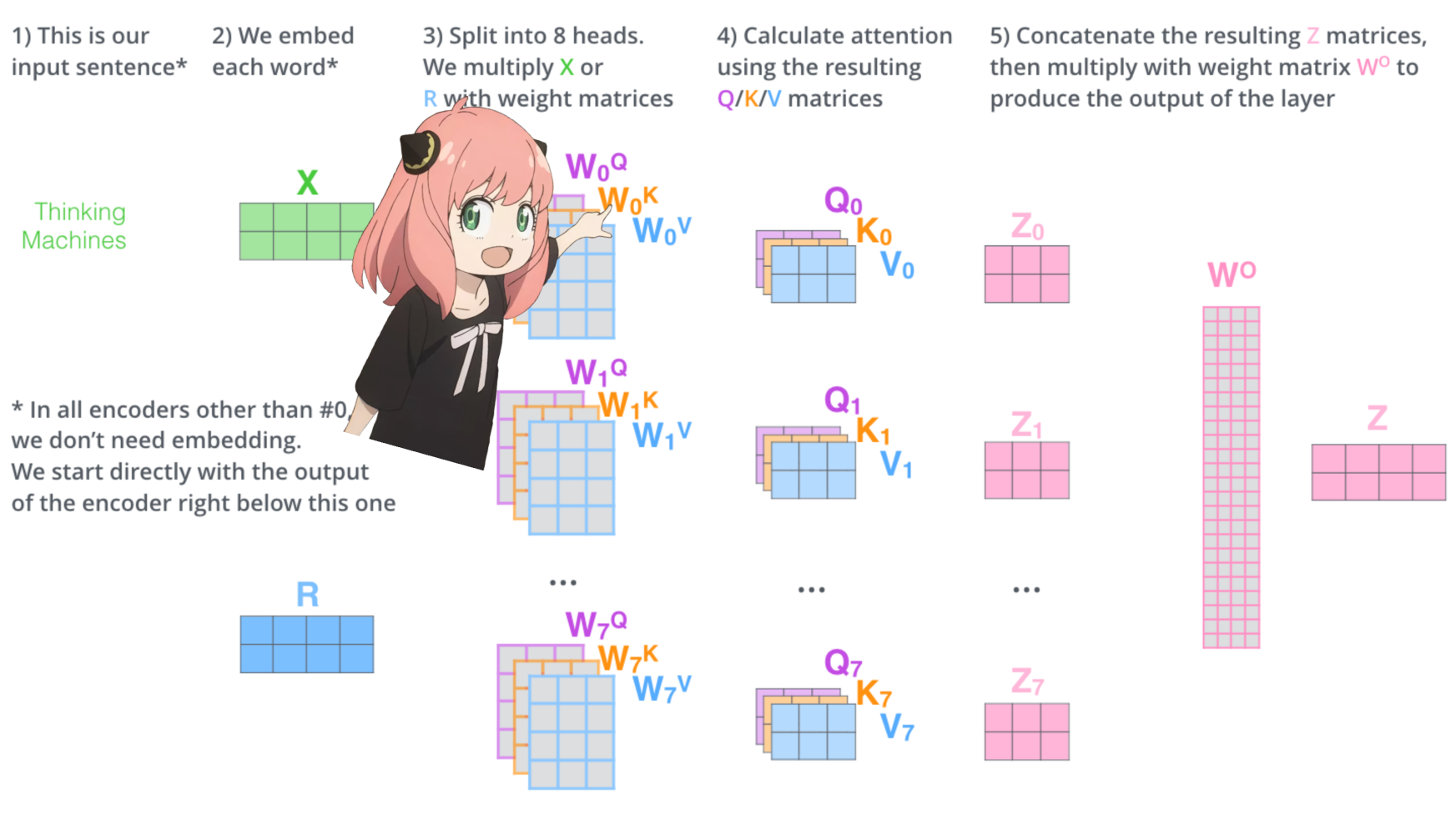
chargeons les têtes d'attention de la première couche du transformateur
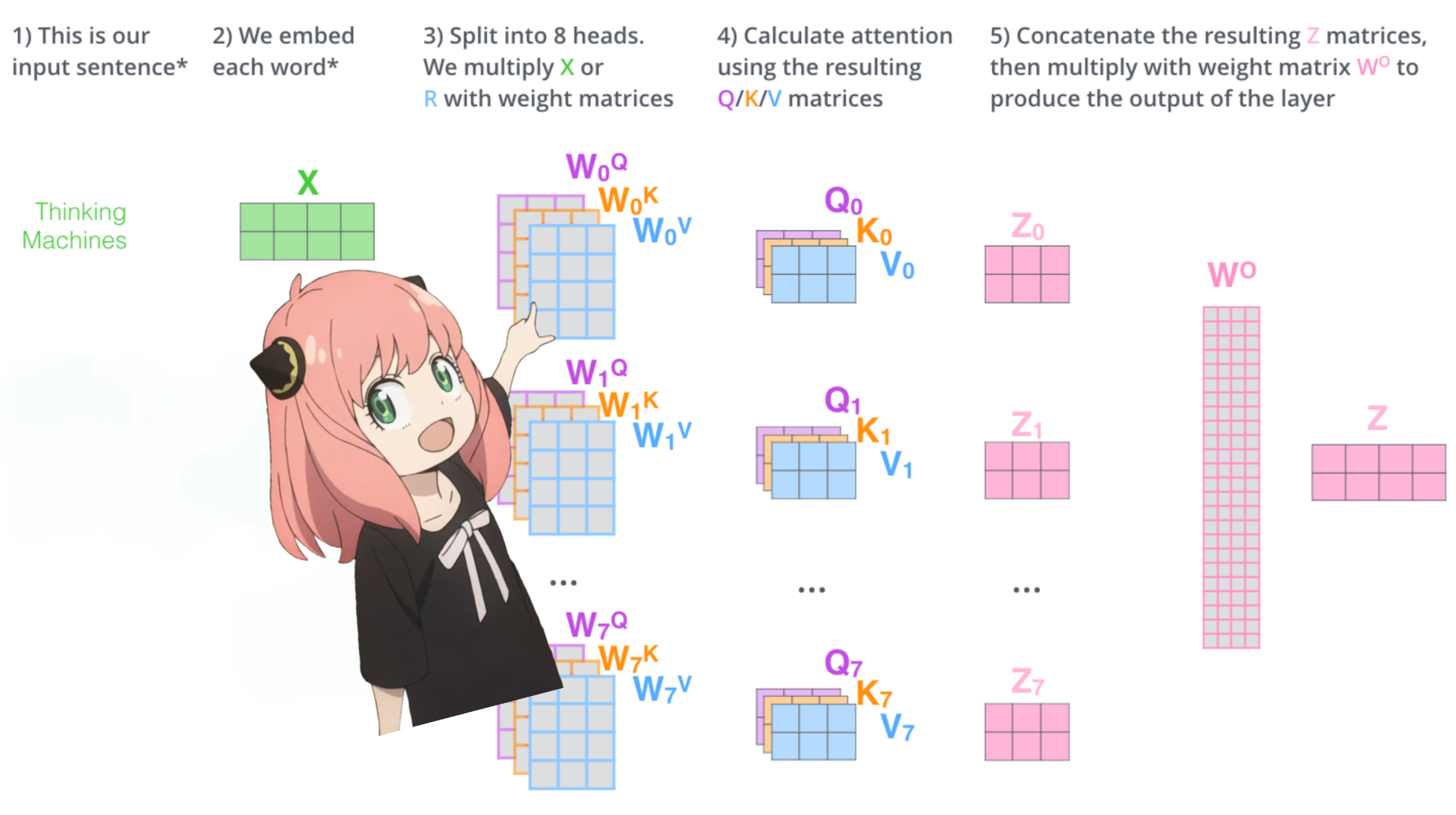
> lorsque nous chargeons les vecteurs de requête, de clé, de valeur et de sortie du modèle, nous remarquons que les formes sont [4096x4096], [1024x4096], [1024x4096], [4096x4096]
> à première vue c'est bizarre car idéalement on veut chaque q,k,v et o pour chaque tête individuellement
> les auteurs du code les ont regroupés parce que c'est facile, cela aide à paralléliser la multiplication des têtes d'attention.
> je vais tout déballer...
print (
model [ "layers.0.attention.wq.weight" ]. shape ,
model [ "layers.0.attention.wk.weight" ]. shape ,
model [ "layers.0.attention.wv.weight" ]. shape ,
model [ "layers.0.attention.wo.weight" ]. shape
) torch.Size([4096, 4096]) torch.Size([1024, 4096]) torch.Size([1024, 4096]) torch.Size([4096, 4096])
dans la section suivante, nous déroulerons les requêtes de plusieurs têtes d'attention, la forme résultante est [32x128x4096]
ici, 32 est le nombre de têtes d'attention dans lama3, 128 est la taille du vecteur de requête et 4096 est la taille de l'intégration du jeton
q_layer0 = model [ "layers.0.attention.wq.weight" ]
head_dim = q_layer0 . shape [ 0 ] // n_heads
q_layer0 = q_layer0 . view ( n_heads , head_dim , dim )
q_layer0 . shape torch.Size([32, 128, 4096])
ici, j'accède à la matrice de poids de requête en premier chef de la première couche, la taille de cette matrice de poids de requête est [128x4096]
q_layer0_head0 = q_layer0 [ 0 ]
q_layer0_head0 . shape torch.Size([128, 4096])
ici, vous pouvez voir que la forme résultante est [17x128], car nous avons 17 jetons et pour chaque jeton, il y a une requête de 128 longueurs.

q_per_token = torch . matmul ( token_embeddings , q_layer0_head0 . T )
q_per_token . shape torch.Size([17, 128])
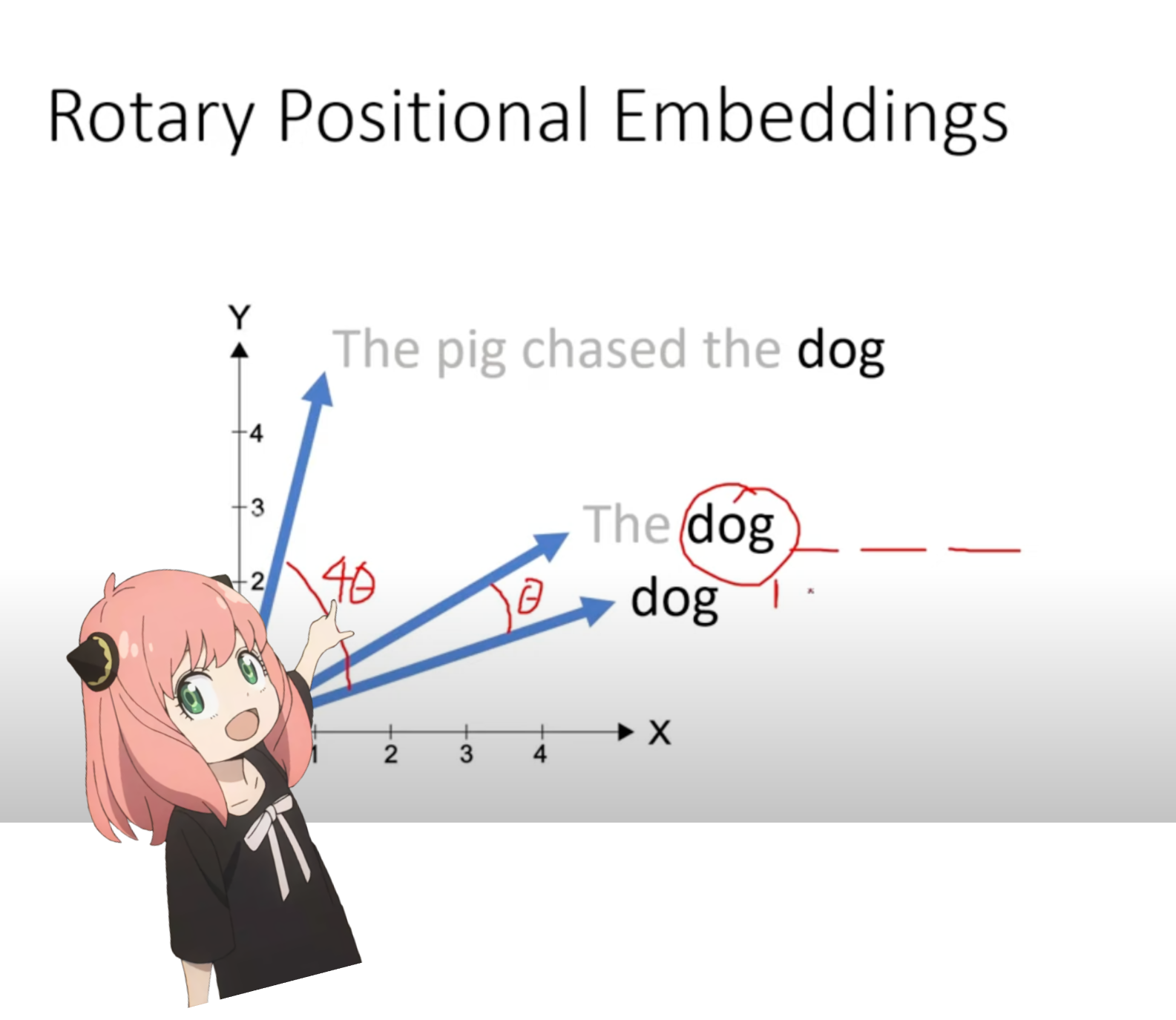
nous sommes maintenant à un stade où nous avons un vecteur de requête pour chaque jeton dans notre invite, mais si vous y réfléchissez, le vecteur de requête individuellement n'a aucune idée de la position dans l'invite.
requête : "la réponse à la question ultime de la vie, de l'univers et de tout est"
dans notre invite, nous avons utilisé "le" trois fois, nous avons besoin que les vecteurs de requête des 3 jetons "le" aient des vecteurs de requête différents (chacun de taille [1x128]) en fonction de leurs positions dans la requête. nous effectuons ces rotations en utilisant RoPE (rotory positional embedding).
regardez cette vidéo (c'est ce que j'ai regardé) pour comprendre les mathématiques. https://www.youtube.com/watch?v=o29P0Kpobz0&t=530s
q_per_token_split_into_pairs = q_per_token . float (). view ( q_per_token . shape [ 0 ], - 1 , 2 )
q_per_token_split_into_pairs . shape torch.Size([17, 64, 2])
dans l'étape ci-dessus, nous divisons les vecteurs de requête en paires, nous appliquons un décalage d'angle de rotation à chaque paire !
nous avons maintenant un vecteur de taille [17x64x2], il s'agit des requêtes de 128 longueurs divisées en 64 paires pour chaque jeton dans l'invite ! chacune de ces 64 paires subira une rotation de m*(theta) où m est la position du jeton pour lequel nous faisons tourner la requête !

zero_to_one_split_into_64_parts = torch . tensor ( range ( 64 )) / 64
zero_to_one_split_into_64_parts tensor([0.0000, 0.0156, 0.0312, 0.0469, 0.0625, 0.0781, 0.0938, 0.1094, 0.1250,
0.1406, 0.1562, 0.1719, 0.1875, 0.2031, 0.2188, 0.2344, 0.2500, 0.2656,
0.2812, 0.2969, 0.3125, 0.3281, 0.3438, 0.3594, 0.3750, 0.3906, 0.4062,
0.4219, 0.4375, 0.4531, 0.4688, 0.4844, 0.5000, 0.5156, 0.5312, 0.5469,
0.5625, 0.5781, 0.5938, 0.6094, 0.6250, 0.6406, 0.6562, 0.6719, 0.6875,
0.7031, 0.7188, 0.7344, 0.7500, 0.7656, 0.7812, 0.7969, 0.8125, 0.8281,
0.8438, 0.8594, 0.8750, 0.8906, 0.9062, 0.9219, 0.9375, 0.9531, 0.9688,
0.9844])
freqs = 1.0 / ( rope_theta ** zero_to_one_split_into_64_parts )
freqs tensor([1.0000e+00, 8.1462e-01, 6.6360e-01, 5.4058e-01, 4.4037e-01, 3.5873e-01,
2.9223e-01, 2.3805e-01, 1.9392e-01, 1.5797e-01, 1.2869e-01, 1.0483e-01,
8.5397e-02, 6.9566e-02, 5.6670e-02, 4.6164e-02, 3.7606e-02, 3.0635e-02,
2.4955e-02, 2.0329e-02, 1.6560e-02, 1.3490e-02, 1.0990e-02, 8.9523e-03,
7.2927e-03, 5.9407e-03, 4.8394e-03, 3.9423e-03, 3.2114e-03, 2.6161e-03,
2.1311e-03, 1.7360e-03, 1.4142e-03, 1.1520e-03, 9.3847e-04, 7.6450e-04,
6.2277e-04, 5.0732e-04, 4.1327e-04, 3.3666e-04, 2.7425e-04, 2.2341e-04,
1.8199e-04, 1.4825e-04, 1.2077e-04, 9.8381e-05, 8.0143e-05, 6.5286e-05,
5.3183e-05, 4.3324e-05, 3.5292e-05, 2.8750e-05, 2.3420e-05, 1.9078e-05,
1.5542e-05, 1.2660e-05, 1.0313e-05, 8.4015e-06, 6.8440e-06, 5.5752e-06,
4.5417e-06, 3.6997e-06, 3.0139e-06, 2.4551e-06])
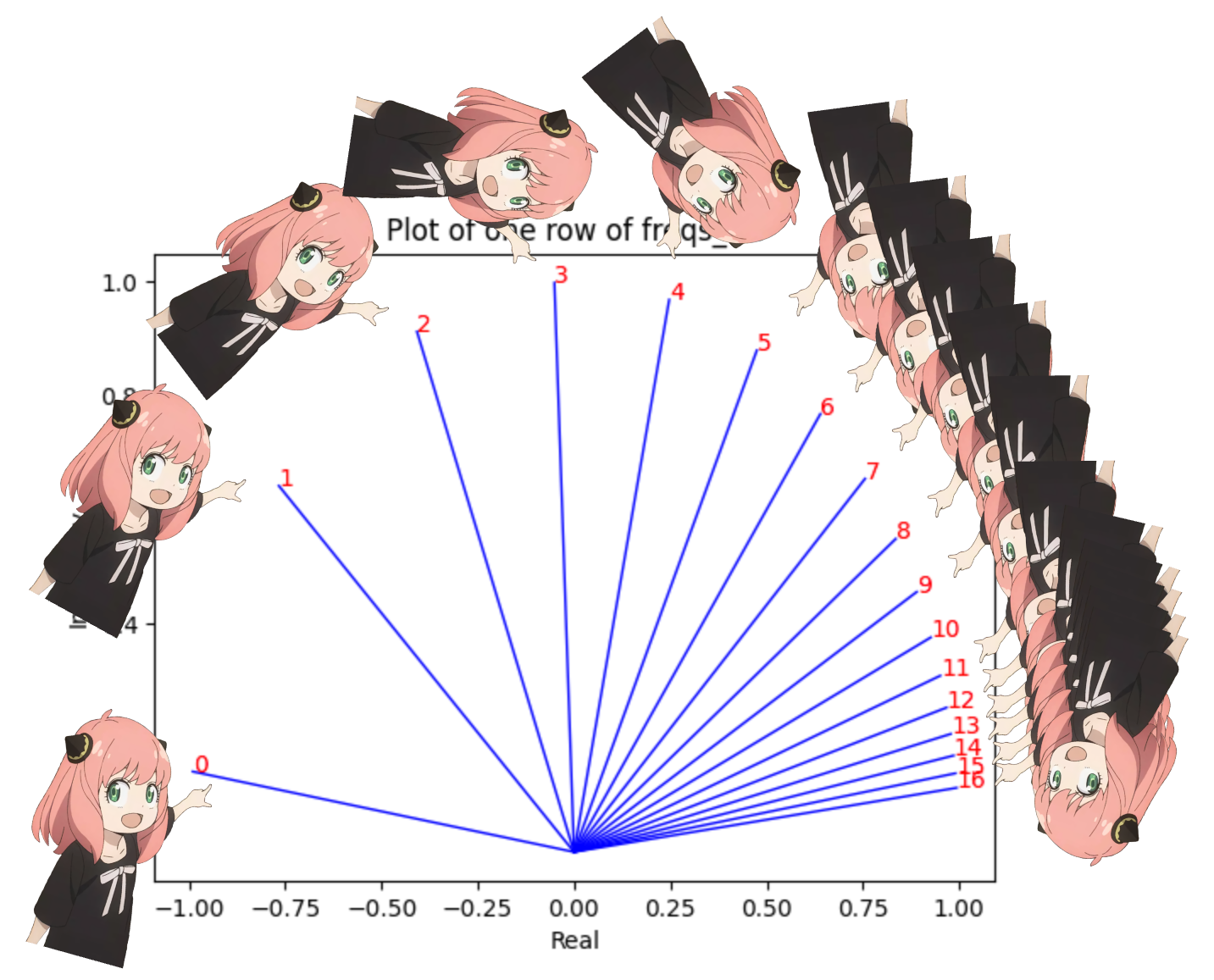
freqs_for_each_token = torch . outer ( torch . arange ( 17 ), freqs )
freqs_cis = torch . polar ( torch . ones_like ( freqs_for_each_token ), freqs_for_each_token )
freqs_cis . shape
# viewing tjhe third row of freqs_cis
value = freqs_cis [ 3 ]
plt . figure ()
for i , element in enumerate ( value [: 17 ]):
plt . plot ([ 0 , element . real ], [ 0 , element . imag ], color = 'blue' , linewidth = 1 , label = f"Index: { i } " )
plt . annotate ( f" { i } " , xy = ( element . real , element . imag ), color = 'red' )
plt . xlabel ( 'Real' )
plt . ylabel ( 'Imaginary' )
plt . title ( 'Plot of one row of freqs_cis' )
plt . show ()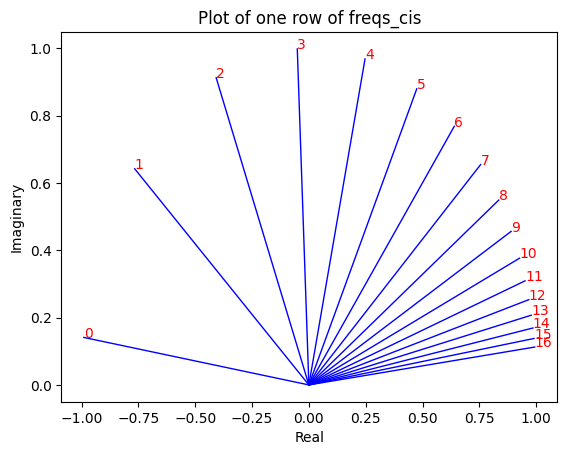
nous pouvons convertir nos requêtes (celle que nous divisons en paires) en nombres complexes, puis en produit scalaire pour faire pivoter la requête en fonction de la position
Honnêtement, c'est beau d'y penser :)
q_per_token_as_complex_numbers = torch . view_as_complex ( q_per_token_split_into_pairs )
q_per_token_as_complex_numbers . shape torch.Size([17, 64])
q_per_token_as_complex_numbers_rotated = q_per_token_as_complex_numbers * freqs_cis
q_per_token_as_complex_numbers_rotated . shape torch.Size([17, 64])
nous pouvons récupérer nos requêtes par paires en visualisant à nouveau les nombres complexes comme des nombres réels
q_per_token_split_into_pairs_rotated = torch . view_as_real ( q_per_token_as_complex_numbers_rotated )
q_per_token_split_into_pairs_rotated . shape torch.Size([17, 64, 2])
les paires pivotées sont maintenant fusionnées, nous avons maintenant un nouveau vecteur de requête (vecteur de requête pivoté) qui a la forme [17x128] où 17 est le nombre de jetons et 128 est la dimension du vecteur de requête
q_per_token_rotated = q_per_token_split_into_pairs_rotated . view ( q_per_token . shape )
q_per_token_rotated . shape torch.Size([17, 128])
k_layer0 = model [ "layers.0.attention.wk.weight" ]
k_layer0 = k_layer0 . view ( n_kv_heads , k_layer0 . shape [ 0 ] // n_kv_heads , dim )
k_layer0 . shape torch.Size([8, 128, 4096])
k_layer0_head0 = k_layer0 [ 0 ]
k_layer0_head0 . shape torch.Size([128, 4096])
k_per_token = torch . matmul ( token_embeddings , k_layer0_head0 . T )
k_per_token . shape torch.Size([17, 128])
k_per_token_split_into_pairs = k_per_token . float (). view ( k_per_token . shape [ 0 ], - 1 , 2 )
k_per_token_split_into_pairs . shape torch.Size([17, 64, 2])
k_per_token_as_complex_numbers = torch . view_as_complex ( k_per_token_split_into_pairs )
k_per_token_as_complex_numbers . shape torch.Size([17, 64])
k_per_token_split_into_pairs_rotated = torch . view_as_real ( k_per_token_as_complex_numbers * freqs_cis )
k_per_token_split_into_pairs_rotated . shape torch.Size([17, 64, 2])
k_per_token_rotated = k_per_token_split_into_pairs_rotated . view ( k_per_token . shape )
k_per_token_rotated . shape torch.Size([17, 128])
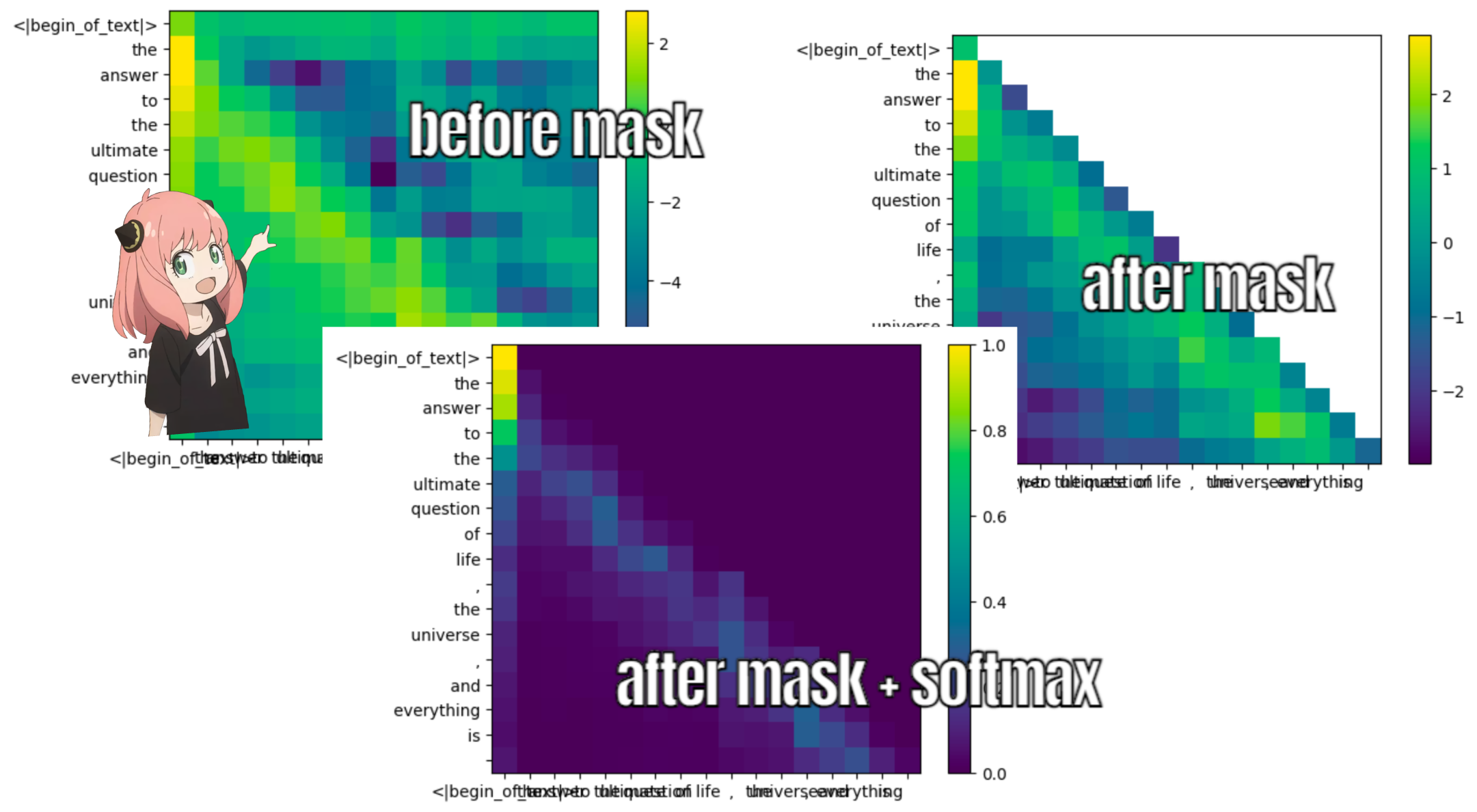
faire cela nous donnera un score mappant chaque jeton les uns avec les autres
ce score décrit dans quelle mesure la requête de chaque jeton est liée à la clé de chaque jeton. C'EST DE L'AUTO-ATTENTION :)
la forme de la matrice de score d'attention (qk_per_token) est [17x17] où 17 est le nombre de jetons dans l'invite
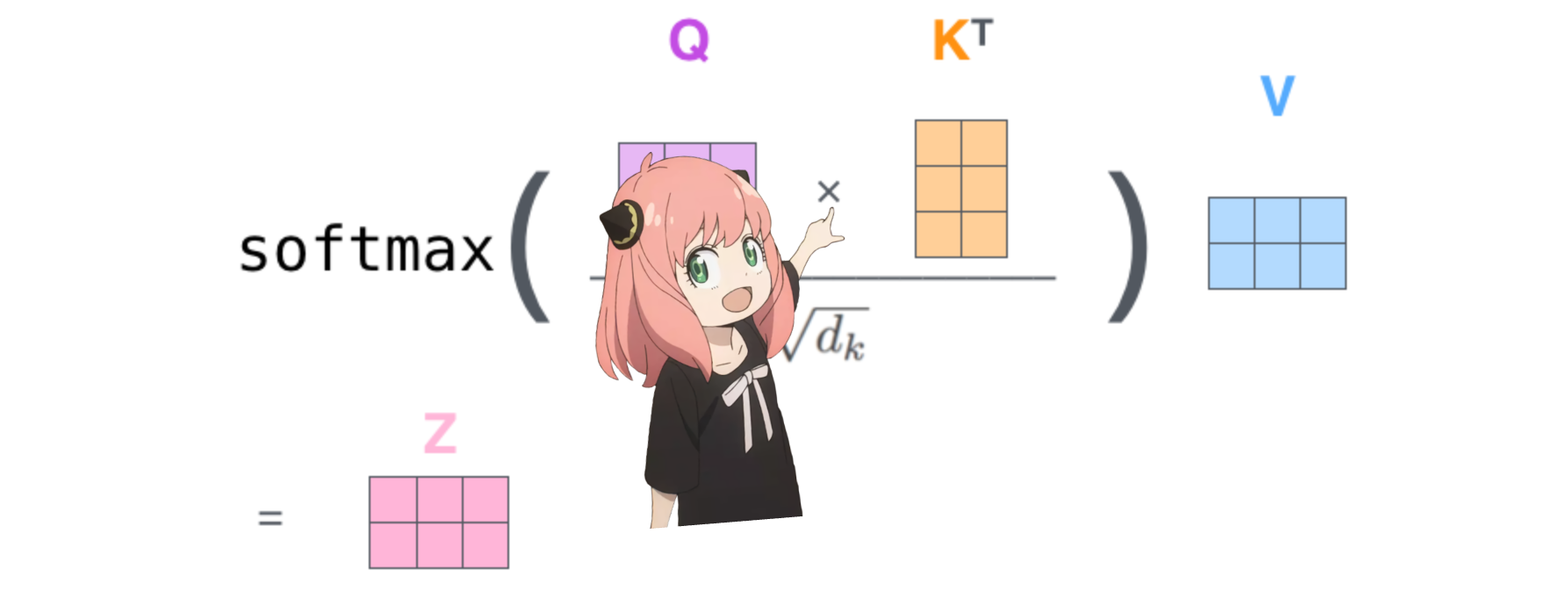
qk_per_token = torch . matmul ( q_per_token_rotated , k_per_token_rotated . T ) / ( head_dim ) ** 0.5
qk_per_token . shape torch.Size([17, 17])
pendant le processus de formation de lama3, les futurs scores qk du jeton sont masqués.
pourquoi ? car pendant la formation, nous apprenons uniquement à prédire les jetons en utilisant les jetons passés.
par conséquent, lors de l'inférence, nous mettons les futurs jetons à zéro.
def display_qk_heatmap ( qk_per_token ):
_ , ax = plt . subplots ()
im = ax . imshow ( qk_per_token . to ( float ). detach (), cmap = 'viridis' )
ax . set_xticks ( range ( len ( prompt_split_as_tokens )))
ax . set_yticks ( range ( len ( prompt_split_as_tokens )))
ax . set_xticklabels ( prompt_split_as_tokens )
ax . set_yticklabels ( prompt_split_as_tokens )
ax . figure . colorbar ( im , ax = ax )
display_qk_heatmap ( qk_per_token )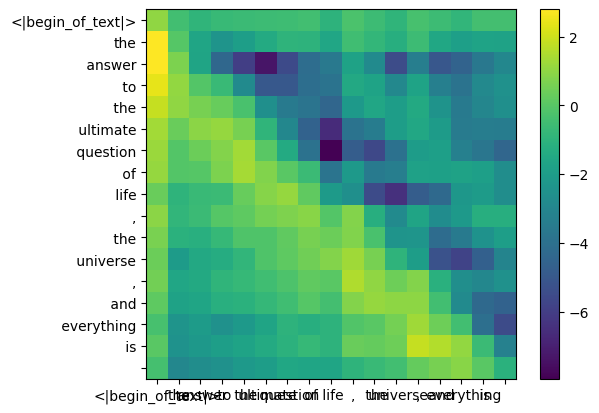
mask = torch . full (( len ( tokens ), len ( tokens )), float ( "-inf" ), device = tokens . device )
mask = torch . triu ( mask , diagonal = 1 )
mask tensor([[0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., -inf, -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., -inf],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]])
qk_per_token_after_masking = qk_per_token + mask
display_qk_heatmap ( qk_per_token_after_masking )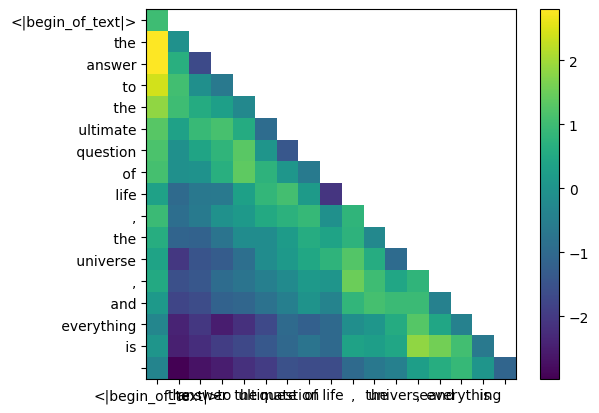
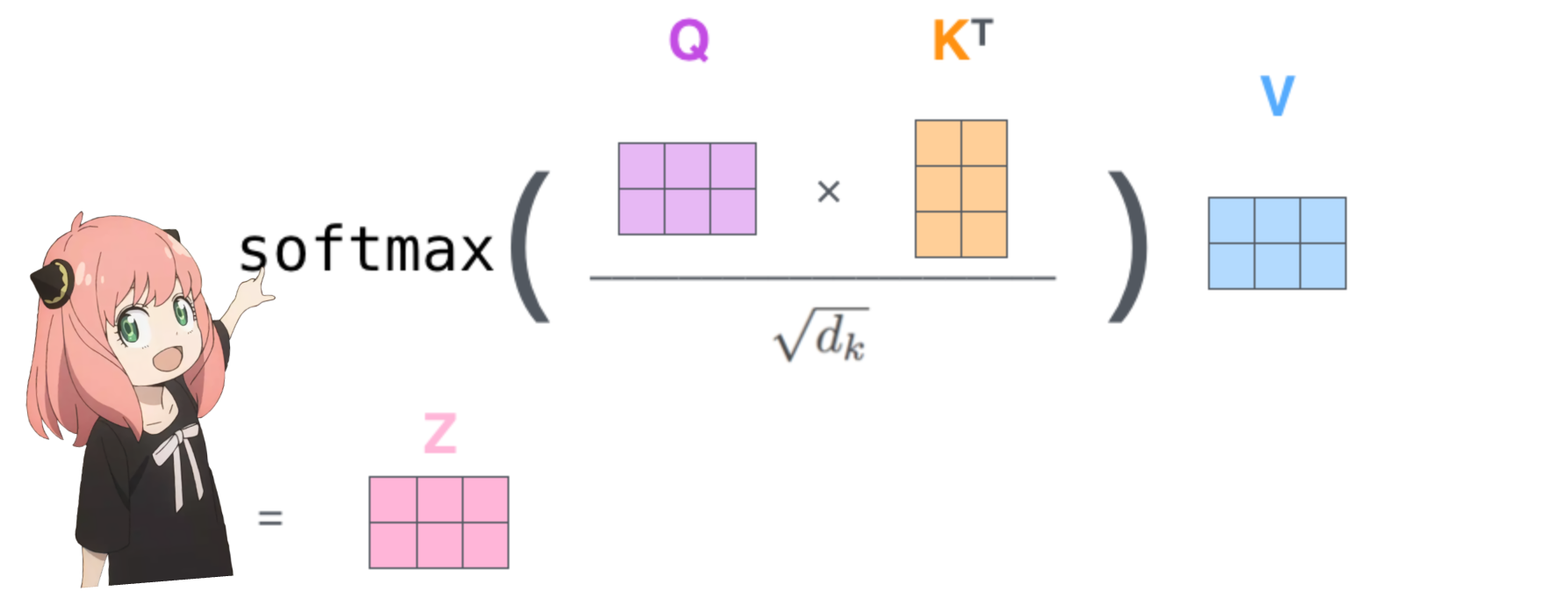
qk_per_token_after_masking_after_softmax = torch . nn . functional . softmax ( qk_per_token_after_masking , dim = 1 ). to ( torch . bfloat16 )
display_qk_heatmap ( qk_per_token_after_masking_after_softmax )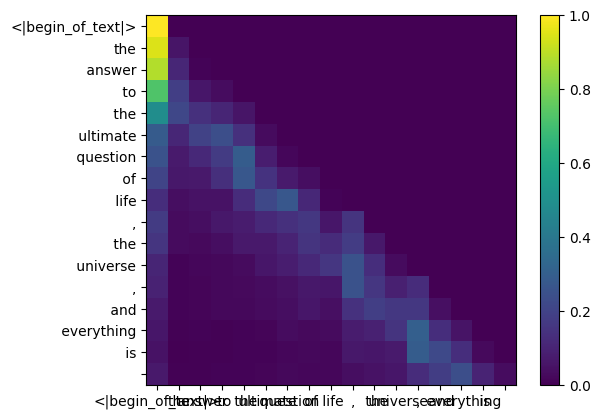
v_layer0 = model [ "layers.0.attention.wv.weight" ]
v_layer0 = v_layer0 . view ( n_kv_heads , v_layer0 . shape [ 0 ] // n_kv_heads , dim )
v_layer0 . shape torch.Size([8, 128, 4096])
la première couche, la première matrice de poids de valeur de tête est donnée ci-dessous
v_layer0_head0 = v_layer0 [ 0 ]
v_layer0_head0 . shape torch.Size([128, 4096])
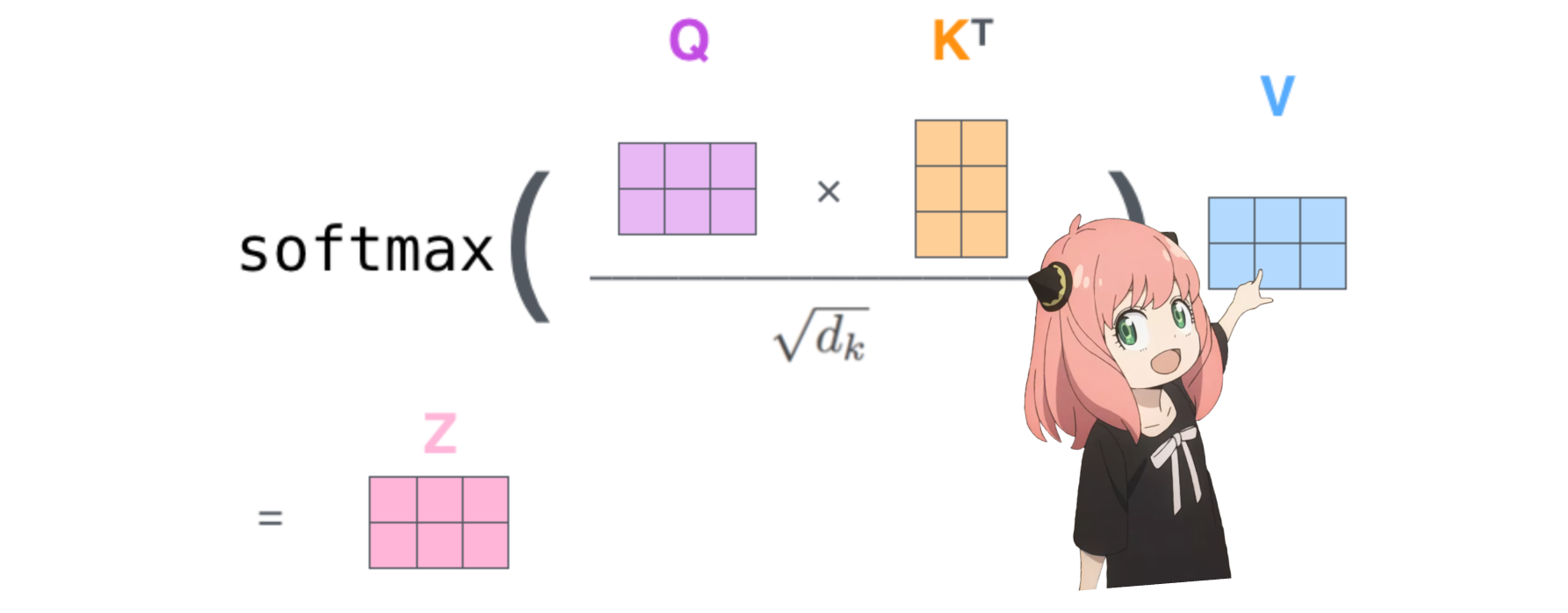
v_per_token = torch . matmul ( token_embeddings , v_layer0_head0 . T )
v_per_token . shape torch.Size([17, 128])
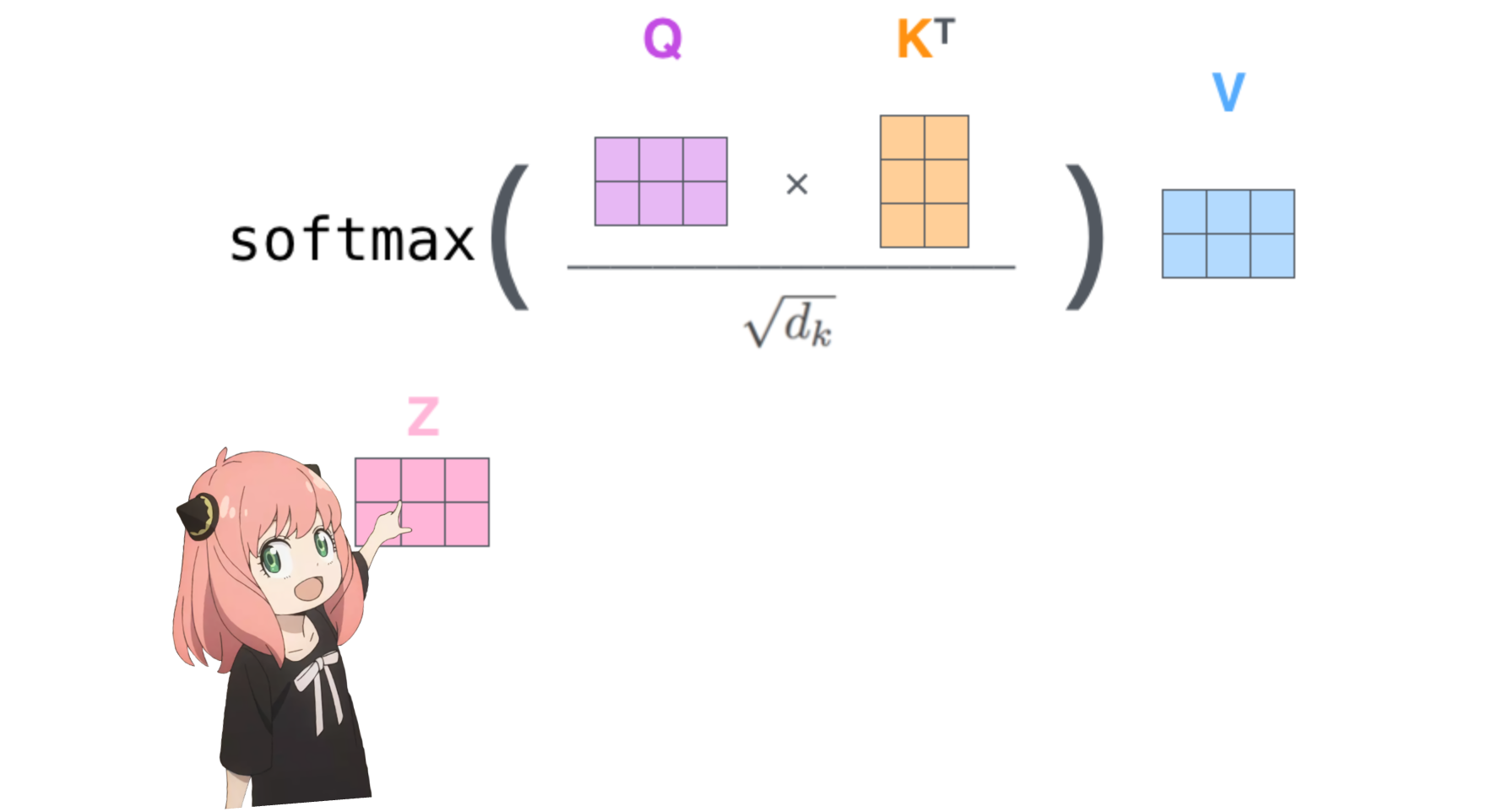
qkv_attention = torch . matmul ( qk_per_token_after_masking_after_softmax , v_per_token )
qkv_attention . shape torch.Size([17, 128])
