greta.gam vous permet d'utiliser les fonctions plus fluides et la syntaxe de formule de mgcv pour définir des termes fluides à utiliser dans un modèle greta. Vous pouvez ensuite définir votre propre probabilité de compléter le modèle et l'ajuster par MCMC.
C'est un travail en cours !
Voici un exemple simple adapté du fichier d'aide mgcv ?gam :
En mgcv :
library( mgcv )
# > Loading required package: nlme
# > This is mgcv 1.9-1. For overview type 'help("mgcv-package")'.
set.seed( 2 )
# simulate some data...
dat <- gamSim( 1 , n = 400 , dist = " normal " , scale = 0.3 )
# > Gu & Wahba 4 term additive model
# fit a model using gam()
b <- gam( y ~ s( x2 ), data = dat ) Maintenant, j'adapte le même modèle dans greta :
library( greta.gam )
# > Loading required package: greta
# >
# > Attaching package: 'greta'
# > The following objects are masked from 'package:stats':
# >
# > binomial, cov2cor, poisson
# > The following objects are masked from 'package:base':
# >
# > %*%, apply, backsolve, beta, chol2inv, colMeans, colSums, diag,
# > eigen, forwardsolve, gamma, identity, rowMeans, rowSums, sweep,
# > tapply
set.seed( 2024 - 02 - 09 )
# setup the linear predictor for the smooth
z <- smooths( ~ s( x2 ), data = dat )
# > ℹ Initialising python and checking dependencies, this may take a moment.
# > ✔ Initialising python and checking dependencies ... done!
# set the distribution of the response
distribution( dat $ y ) <- normal( z , 1 )
# make some prediction data
pred_dat <- data.frame ( x2 = seq( 0 , 1 , length.out = 100 ))
# z_pred stores the predictions
z_pred <- evaluate_smooths( z , newdata = pred_dat )
# build model
m <- model( z_pred )
# draw from the posterior
draws <- mcmc( m , n_samples = 200 )
# > running 4 chains simultaneously on up to 8 CPU cores
#> warmup 0/1000 | eta: ?s warmup == 50/1000 | eta: 30s warmup ==== 100/1000 | eta: 17s warmup ====== 150/1000 | eta: 12s warmup ======== 200/1000 | eta: 10s warmup ========== 250/1000 | eta: 8s warmup =========== 300/1000 | eta: 7s warmup ============= 350/1000 | eta: 6s warmup =============== 400/1000 | eta: 5s warmup ================= 450/1000 | eta: 5s warmup =================== 500/1000 | eta: 4s warmup ===================== 550/1000 | eta: 4s warmup ======================= 600/1000 | eta: 3s warmup ========================= 650/1000 | eta: 3s warmup =========================== 700/1000 | eta: 2s warmup ============================ 750/1000 | eta: 2s warmup ============================== 800/1000 | eta: 1s warmup ================================ 850/1000 | eta: 1s warmup ================================== 900/1000 | eta: 1s warmup ==================================== 950/1000 | eta: 0s warmup ====================================== 1000/1000 | eta: 0s
# > sampling 0/200 | eta: ?s sampling ========== 50/200 | eta: 1s sampling =================== 100/200 | eta: 0s sampling ============================ 150/200 | eta: 0s sampling ====================================== 200/200 | eta: 0s
# plot the mgcv fit
plot( b , scheme = 1 , shift = coef( b )[ 1 ])
# add in a line for each posterior sample
apply( draws [[ 1 ]], 1 , lines , x = pred_dat $ x2 , col = " blue " )
# > NULL
# plot the data
points( dat $ x2 , dat $ y , pch = 19 , cex = 0.2 )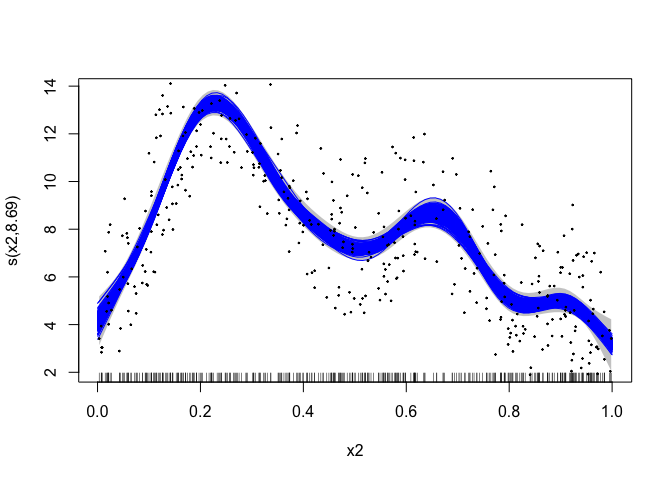
greta.gam utilise quelques astuces de la routine jagam (Wood, 2016) dans mgcv pour faire fonctionner les choses. Voici quelques brefs détails pour ceux qui s’intéressent au fonctionnement interne…
Les GAM sont des modèles avec des interprétations bayésiennes (même lorsqu'ils sont ajustés à l'aide de méthodes « fréquentistes »). On peut considérer la matrice de pénalité plus lisse comme une matrice de précision a priori dans un modèle bayésien à effets aléatoires. Les matrices de conception sont construites exactement comme dans le cas fréquentiste. Voir Miller (2021) pour plus d’informations à ce sujet.
Il y a une légère difficulté dans l'interprétation bayésienne du GAM dans la mesure où, dans leur forme naïve, les a priori sont impropres en tant qu'espace nul de la pénalité (dans le cas 1D, généralement le terme linéaire). Pour obtenir des a priori corrects, nous pouvons utiliser l’une des « astuces » employées dans Marra & Wood (2011) : pénaliser d’une manière ou d’une autre les parties de la pénalité qui conduisent à l’a priori inapproprié. Nous prenons l'option proposée par jagam et créons une matrice de pénalité supplémentaire pour ces termes (à partir d'une décomposition propre de la matrice de pénalité ; voir Marra & Wood, 2011).
Marra, G et Wood, SN (2011) Sélection pratique de variables pour les modèles additifs généralisés. Statistiques informatiques et analyse des données, 55, 2372-2387.
Miller DL (2021). Vues bayésiennes de la modélisation additive généralisée. arXiv.
Wood, SN (2016) Juste un autre modélisateur additif Gibbs : interfacer JAGS et mgcv. Journal des logiciels statistiques 75, non. 7