La deuxième édition de ce livre a été publiée. Toutes les mises à jour de contenu après mai 2019 se réfèrent à la première impression de la deuxième édition.
Pour le contenu de la première édition, voir Release first_edition
[TOC]
Pour faciliter l'apprentissage, quelques descriptions d'outils sont compilées.
Si vous devez référencer ce Repo :
Format : SmirkCao, Lihang, (2018), GitHub repository, https://github.com/SmirkCao/Lihang
ou
@misc{SmirkCao,
author = {SmirkCao},
title = {Lihang},
year = {2018},
publisher = {GitHub},
journal = {GitHub repository},
howpublished = {url{https://github.com/SmirkCao/Lihang}},
commit = {c5624a9bd757a5cc88e78b85b89e9221deb08270}
}
Cette partie du contenu ne correspond pas à la préface de « Méthodes d'apprentissage statistique ». La préface du livre est également bien écrite et est citée comme suit :
- En termes de sélection de contenu, nous nous concentrons sur l'introduction des méthodes les plus importantes et les plus couramment utilisées, en particulier les méthodes liées aux problèmes de classification et d'étiquetage .
- Essayez d'utiliser un cadre unifié pour discuter de toutes les méthodes afin que l'ensemble du livre ne perde pas son caractère systématique.
- Applicable aux étudiants universitaires et aux étudiants diplômés se spécialisant en recherche d'informations et en traitement du langage naturel.
Une autre chose à noter est le parcours professionnel de l’auteur.
L'auteur a participé à des recherches sur divers traitements intelligents de données textuelles à l'aide de méthodes d'apprentissage statistique, notamment le traitement du langage naturel, la récupération d'informations et l'exploration de données textuelles.
Si vous utilisez mon modèle pour mettre en œuvre la recherche de similarité, le livre qui est similaire au livre de M. Li est "Semiconductor Optoelectronic Devices". C'est dommage que je ne l'ai pas étudié à plusieurs reprises quand j'étais jeune.
J'espère qu'au fil des lectures répétées, le livre entier deviendra de plus en plus épais. Tous les documents et codes de cette série, sauf indication contraire, font référence aux « Méthodes d'apprentissage statistique » de Li Hang. Le contenu d'autres références sera lié s'il est cité.
Certaines références sont répertoriées dans les références, dont certaines sont très utiles pour comprendre le contenu du livre. Les descriptions et explications de ces fichiers seront ajoutées dans Refs/README.md correspondant à la section de référence. Quelques notes sur d'autres références ont également été ajoutées à ce document.
Pour faciliter le téléchargement des références, ref_downloader.sh a été ajouté lors de review02, qui peut être utilisé pour télécharger les références répertoriées dans le livre. Le processus de mise à jour se termine progressivement au fur et à mesure de la progression de review02.
De plus, ce livre du professeur Li Hang, C'est vraiment fin (la deuxième version n'est plus fine) , mais presque chaque phrase fait ressortir de nombreux points et mérite d'être lue encore et encore.
Il y a une table des symboles après la table des matières dans le livre, qui explique les définitions des symboles, donc s'il y a des symboles que vous ne comprenez pas, vous pouvez les rechercher dans le tableau, il y a un index à la fin du livre ; et vous pouvez utiliser l'index pour trouver la signification du symbole correspondant qui apparaît dans le livre Emplacement. Dans ce Repo, un glossary_index.md est maintenu pour ajouter quelques explications aux symboles correspondants et marquer directement les numéros de page correspondant aux symboles. La progression sera mise à jour avec la révision.
Après chaque algorithme ou exemple, il y aura un ◼️, indiquant que l'algorithme ou l'exemple se termine ici. C'est ce qu'on appelle le symbole de fin de preuve. Vous le saurez si vous lisez davantage de littérature.
Lors de la lecture, nous nous posons souvent des questions sur la base des logarithmes. Certaines des plus importantes sont soulignées dans le livre. Certains qui ne sont pas soulignés peuvent être compris à travers le contexte. De plus, comme il existe une formule pour changer la base, peu importe la nature de la base. La différence réside dans un coefficient constant. Cependant, le choix de différentes bases aura des significations physiques et des considérations de résolution de problèmes. Pour analyser ce problème, vous pouvez consulter la discussion sur l'entropie dans PRML 1.6 pour comprendre.
De plus, en ce qui concerne la question des coefficients constants dans la formule, si une solution itérative est utilisée et que parfois la formule est simplifiée dans une certaine mesure, la vitesse de convergence peut être améliorée. Les détails peuvent être progressivement compris dans la pratique.
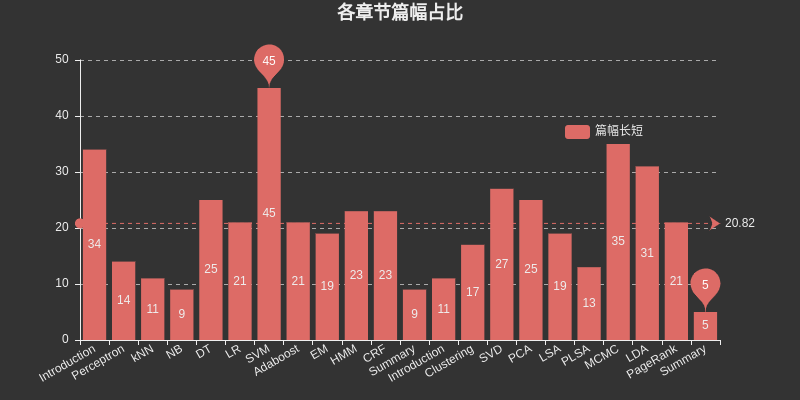
Insérez un graphique ici pour répertorier l'espace occupé par chaque chapitre. Parmi eux, SVM occupe le plus grand espace parmi l'apprentissage supervisé, MCMC occupe le plus grand espace parmi l'apprentissage non supervisé, et DT, HMM, CRF, SVD, PCA, LDA et Le PageRank occupe également le plus grand espace relativement grand.
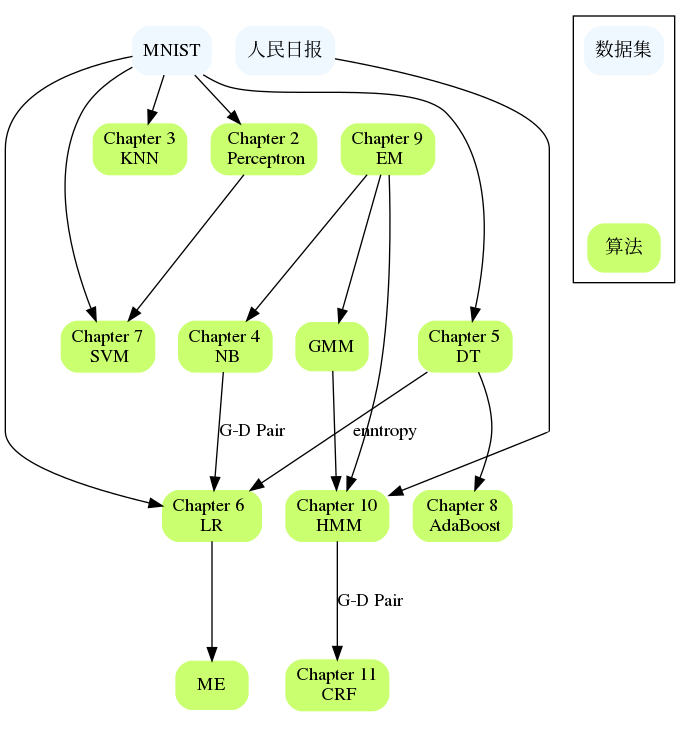
Les chapitres sont liés les uns aux autres, comme NB et LR, DT et AdaBoost, Perceptron et SVM, HMM et CRF, etc. Si vous rencontrez des difficultés dans un chapitre volumineux, vous pouvez revoir le contenu des chapitres précédents ou vérifier les références de chapitres spécifiques sont généralement donnés qui décrivent le problème plus en détail et peuvent expliquer où vous êtes bloqué.
Introduction
Trois éléments des méthodes d'apprentissage statistique :
Modèle
Stratégie
algorithme
La deuxième édition a réorganisé la structure des répertoires de ce chapitre pour la rendre plus claire.
Perceptron
kNN
N.-B.
DT
LR
Concernant l'étude de l'entropie maximale, il est recommandé de lire la littérature de référence [1] dans ce chapitre, Berger, 1996, qui est utile pour comprendre les exemples du livre et appréhender le principe de l'entropie maximale.
Alors pourquoi LR et Maxent sont-ils placés dans un seul chapitre ?
Tous appartiennent au modèle linéaire logarithmique
Les deux peuvent être utilisés pour la classification binaire et la multi-classification
Les méthodes d'apprentissage des deux modèles utilisent généralement l'estimation du maximum de vraisemblance, ou l'estimation du maximum de vraisemblance régularisée. Elle peut être formalisée comme un problème d'optimisation sans contrainte, et les méthodes de solution incluent IIS, GD, BFGS, etc.
Il est décrit comme suit dans Régression logistique,
La régression logistique, malgré son nom, est un modèle linéaire de classification plutôt que de régression. La régression logistique est également connue dans la littérature sous le nom de régression logit, classification à entropie maximale (MaxEnt) ou classificateur log-linéaire. Dans ce modèle, les probabilités décrivent. les résultats possibles d'un seul essai sont modélisés à l'aide d'une fonction logistique.
Il y a aussi une telle description
La régression logistique est un cas particulier d'entropie maximale avec deux étiquettes +1 et −1.
La dérivation dans ce chapitre utilise la propriété de $yin mathcal{Y}={0,1}$
Parfois on dit que la régression logistique s'appelle Maxent en PNL
SVM
Booster
Décomposons-le ici, car HMM et CRF conduisent généralement à l'introduction de modèles graphiques probabilistes. Dans "Machine Learning, Zhou Zhihua", un chapitre distinct sur le modèle graphique probabiliste est utilisé pour inclure HMM, MRF, CRF et d'autres contenus. De plus, il existe de nombreux points liés entre HMM et CRF lui-même.
Dans le premier chapitre du livre, trois applications de l'apprentissage supervisé sont expliquées : la classification, l'étiquetage et la régression. Il y a des suppléments au chapitre 12. Ce livre considère principalement les méthodes d'apprentissage des deux premiers. En conséquence, la segmentation est également appropriée ici. Le modèle de classification est introduit plus tôt et la régression est mentionnée dans une petite partie. Le problème de l'étiquetage est principalement introduit plus tard.
EM
L'algorithme EM est un algorithme itératif utilisé pour l'estimation du maximum de vraisemblance des paramètres du modèle probabiliste contenant des variables cachées, ou pour l'estimation de la probabilité postérieure maximale. (L'estimation du maximum de vraisemblance et l'estimation du maximum de probabilité postérieure sont ici des stratégies d'apprentissage )
Si les variables du modèle probabiliste sont toutes des variables observées, alors étant donné les données, les paramètres du modèle peuvent être estimés directement à l'aide de la méthode d'estimation du maximum de vraisemblance ou de la méthode d'estimation bayésienne.
Notez que si vous ne comprenez pas cette description dans le livre, veuillez vous référer à la partie estimation des paramètres de la méthode Naive Bayes dans CH04.
Cette partie du code implémente BMM et GMM, cela vaut la peine d'y jeter un oeil
Concernant EM, peu de choses ont été écrites sur ce chapitre. EM et Hinton sont étroitement liés. Ils ont publié le deuxième article de Capsule Network "Matrix Capsules with EM Routing" à l'ICLR en 2018.
Dans CH22, l'algorithme EM est classé comme méthode d'apprentissage automatique de base et n'implique pas de modèles d'apprentissage automatique spécifiques. Il peut être utilisé pour l'apprentissage non supervisé, l'apprentissage supervisé et l'apprentissage semi-supervisé.
HMM
FRC
Résumé
Ce chapitre ne comporte que quelques pages. Vous pouvez envisager la routine de lecture suivante :
Lisez-le avec le chapitre 1
Si vous rencontrez des questions peu claires dans des études précédentes, relisez ce chapitre.
Lisez ce chapitre attentivement et développez ce chapitre en dix autres chapitres.
Notez qu'il y a la figure 12.2 dans ce chapitre, qui mentionne que la fonction de perte logistique $y$ doit être définie ici dans $cal{Y}={+1,-1}$. LR a été introduit plus tôt lorsque $y$ est. défini à $cal{Y}={0,1}$, veuillez faire attention ici.
Le livre du Maître Li vous fait vraiment gagner quelque chose de nouveau à chaque fois que vous le lisez.
La deuxième édition ajoute huit méthodes d'apprentissage non supervisées : clustering, décomposition en valeurs singulières, analyse en composantes principales, analyse sémantique latente, analyse sémantique latente probabiliste, méthode de Monte Carlo par chaîne de Markov, allocation de Dirichlet latente et PageRank.
Introduction
Regroupement
Chaque chapitre de ce livre n'est pas complètement indépendant. Cette partie espère organiser les connexions entre les chapitres et les ensembles de données applicables. La mesure dans laquelle l’algorithme est mis en œuvre et les ensembles de données sur lesquels il peut s’exécuter constituent également un aspect.