Détection des valeurs aberrantes Python (PyOD)
Déploiement & Documentation & Statistiques & Licence

Lisez-moi d'abord
Bienvenue dans PyOD, une bibliothèque Python complète mais facile à utiliser pour détecter les anomalies dans les données multivariées. Que vous vous attaquiez à un projet à petite échelle ou à de grands ensembles de données, PyOD propose une gamme d'algorithmes adaptés à vos besoins.
- Pour la détection des valeurs aberrantes dans les séries chronologiques , veuillez utiliser TODS.
- Pour la détection des valeurs aberrantes du graphique , veuillez utiliser PyGOD.
- Comparaison des performances et ensembles de données : nous disposons d'un document de référence complet de 45 pages sur la détection des anomalies. ADBench, entièrement open source, compare 30 algorithmes de détection d'anomalies sur 57 ensembles de données de référence.
- En savoir plus sur la détection des anomalies sur Anomaly Detection Resources
- PyOD sur les systèmes distribués : vous pouvez également exécuter PyOD sur des databricks.
À propos de PyOD
PyOD, créée en 2017, est devenue une bibliothèque Python incontournable pour détecter les objets anormaux/aberrants dans les données multivariées. Ce domaine passionnant mais stimulant est communément appelé détection des valeurs aberrantes ou détection des anomalies.
PyOD comprend plus de 50 algorithmes de détection, du LOF classique (SIGMOD 2000) aux pointes ECOD et DIF (TKDE 2022 et 2023). Depuis 2017, PyOD a été utilisé avec succès dans de nombreux projets de recherche universitaire et produits commerciaux avec plus de 22 millions de téléchargements. Il est également bien reconnu par la communauté du machine learning avec divers articles/tutoriels dédiés, notamment Analytics Vidhya, KDnuggets et Towards Data Science.
PyOD est proposé pour :
- Interface unifiée et conviviale pour divers algorithmes.
- Large gamme de modèles , des techniques classiques aux dernières méthodes d'apprentissage en profondeur dans PyTorch .
- Hautes performances et efficacité , tirant parti de numba et joblib pour la compilation JIT et le traitement parallèle.
- Fast Training & Prediction , réalisé grâce au cadre SUOD [50].
Détection des valeurs aberrantes avec 5 lignes de code :
# Example: Training an ECOD detector
from pyod . models . ecod import ECOD
clf = ECOD ()
clf . fit ( X_train )
y_train_scores = clf . decision_scores_ # Outlier scores for training data
y_test_scores = clf . decision_function ( X_test ) # Outlier scores for test data
Choisir le bon algorithme : vous ne savez pas par où commencer ? Considérez ces options robustes et interprétables :
- ECOD : exemple d'utilisation d'ECOD pour la détection des valeurs aberrantes
- Forêt d'isolement : exemple d'utilisation de Forêt d'isolement pour la détection des valeurs aberrantes
Vous pouvez également explorer MetaOD pour une approche basée sur les données.
Citant PyOD :
L'article PyOD est publié dans le Journal of Machine Learning Research (JMLR) (piste MLOSS). Si vous utilisez PyOD dans une publication scientifique, nous apprécierions les citations de l'article suivant :
@article{zhao2019pyod,
auteur = {Zhao, Yue et Nasrullah, Zain et Li, Zheng},
title = {PyOD : une boîte à outils Python pour la détection évolutive des valeurs aberrantes},
journal = {Journal de recherche sur l'apprentissage automatique},
année = {2019},
volume = {20},
nombre = {96},
pages = {1-7},
URL = {http://jmlr.org/papers/v20/19-011.html}
}
ou:
Zhao, Y., Nasrullah, Z. et Li, Z., 2019. PyOD : une boîte à outils Python pour la détection évolutive des valeurs aberrantes. Journal de recherche sur l'apprentissage automatique (JMLR), 20(96), pp.1-7.
Pour une perspective plus large sur la détection des anomalies, consultez nos articles NeurIPS ADBench : Anomaly Detection Benchmark Paper et ADGym : Design Choices for Deep Anomaly Detection :
@article{han2022adbench,
title={Adbench : benchmark de détection d'anomalies},
author={Han, Songqiao et Hu, Xiyang et Huang, Hailiang et Jiang, Minqi et Zhao, Yue},
journal={Avances dans les systèmes de traitement de l'information neuronale},
volume={35},
pages={32142--32159},
année={2022}
}
@article{jiang2023adgym,
title={ADGym : Choix de conception pour la détection des anomalies profondes},
author={Jiang, Minqi et Hou, Chaochuan et Zheng, Ao et Han, Songqiao et Huang, Hailiang et Wen, Qingsong et Hu, Xiyang et Zhao, Yue},
journal={Avances dans les systèmes de traitement de l'information neuronale},
volume={36},
année={2023}
}
Table des matières :
- Installation
- Aide-mémoire et référence de l'API
- Benchmark et ensembles de données ADBench
- Sauvegarde et chargement du modèle
- Train rapide avec SUOD
- Seuil des scores aberrants
- Algorithmes implémentés
- Démarrage rapide pour la détection des valeurs aberrantes
- Comment contribuer
- Critères d'inclusion
Installation
PyOD est conçu pour une installation facile à l'aide de pip ou conda . Nous vous recommandons d'utiliser la dernière version de PyOD en raison des mises à jour et améliorations fréquentes :
pip install pyod # normal install
pip install --upgrade pyod # or update if needed
conda install -c conda-forge pyod
Vous pouvez également cloner et exécuter le fichier setup.py :
git clone https://github.com/yzhao062/pyod.git
cd pyod
pip install .
Dépendances requises :
- Python 3.8 ou supérieur
- joblib
- matplotlib
- numpy> = 1,19
- nombre>=0,51
- scipy>=1.5.1
- scikit_learn>=0.22.0
Dépendances facultatives (voir détails ci-dessous) :
- combo (facultatif, requis pour models/combination.py et FeatureBagging)
- pytorch (facultatif, requis pour AutoEncoder et d'autres modèles d'apprentissage en profondeur)
- suod (facultatif, requis pour exécuter le modèle SUOD)
- xgboost (facultatif, requis pour XGBOD)
- pythresh (facultatif, requis pour le seuillage)
Aide-mémoire et référence de l'API
La référence complète de l'API est disponible sur la documentation PyOD. Vous trouverez ci-dessous une aide-mémoire rapide pour tous les détecteurs :
- fit(X) : Installer le détecteur. Le paramètre y est ignoré dans les méthodes non supervisées.
- Decision_function(X) : Prédisez les scores d'anomalies bruts pour X à l'aide du détecteur équipé.
- Predict(X) : Déterminez si un échantillon est une valeur aberrante ou non sous forme d'étiquettes binaires à l'aide du détecteur ajusté.
- Predict_proba(X) : estime la probabilité qu'un échantillon soit une valeur aberrante à l'aide du détecteur ajusté.
- prédire_confidence(X) : évaluer la confiance du modèle par échantillon (applicable dans prédire et prédire_proba) [35].
Attributs clés d'un modèle ajusté :
- Decision_scores_ : scores aberrants des données d'entraînement. Des scores plus élevés indiquent généralement un comportement plus anormal. Les valeurs aberrantes ont généralement des scores plus élevés.
- labels_ : étiquettes binaires des données d'entraînement, où 0 indique les valeurs internes et 1 indique les valeurs aberrantes/anomalies.
Benchmark et ensembles de données ADBench
Nous venons de publier un ADBench de 45 pages, le plus complet : Anomaly Detection Benchmark [15]. ADBench, entièrement open source, compare 30 algorithmes de détection d'anomalies sur 57 ensembles de données de référence.
L’organisation d’ ADBench est présentée ci-dessous :

Pour une visualisation plus simple, nous effectuons la comparaison des modèles sélectionnés via compare_all_models.py.
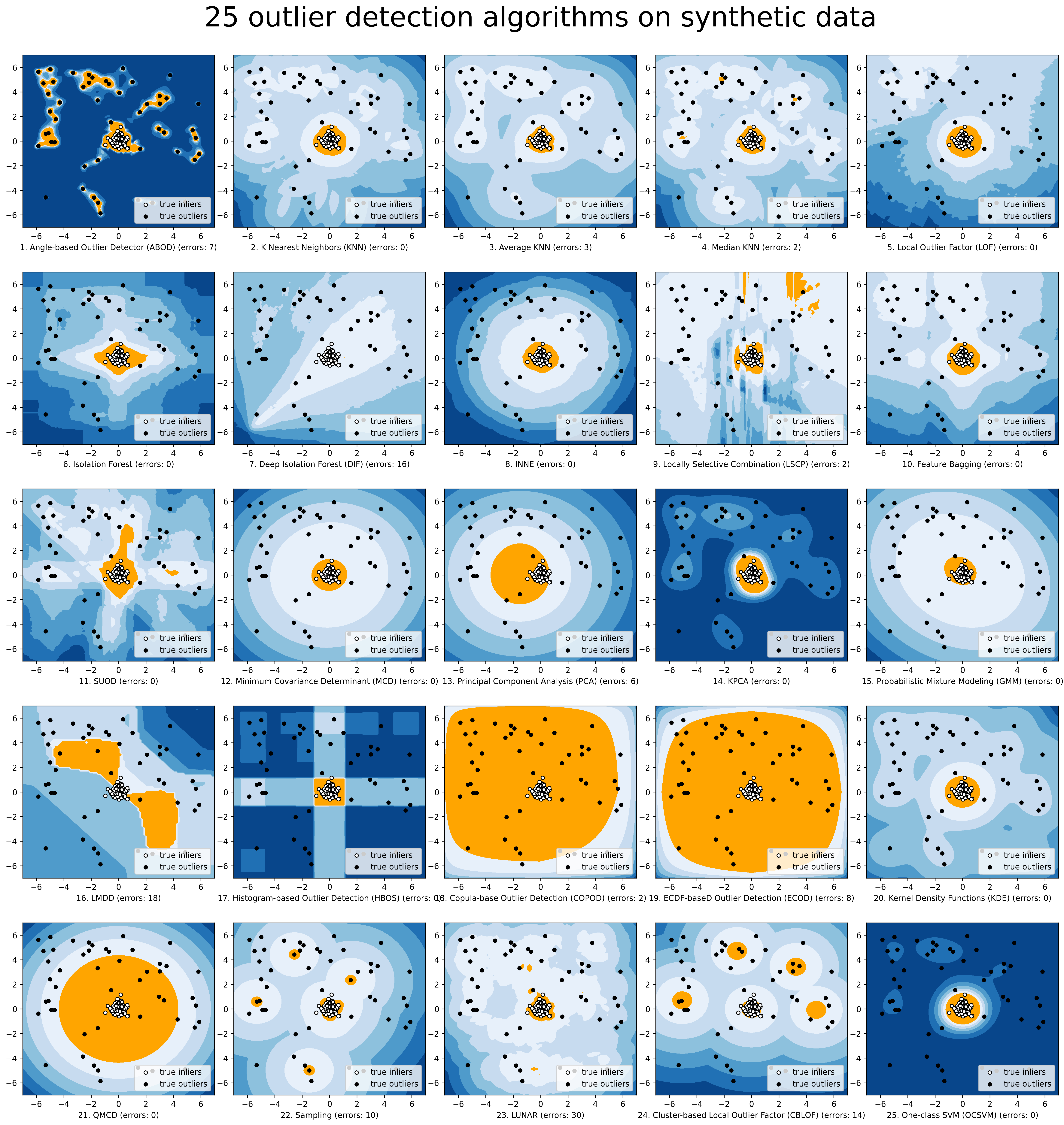
Sauvegarde et chargement du modèle
PyOD adopte une approche similaire à celle de Sklearn concernant la persistance du modèle. Voir la persistance du modèle pour plus de précisions.
En bref, nous vous recommandons d'utiliser joblib ou pickle pour enregistrer et charger les modèles PyOD. Voir "examples/save_load_model_example.py" pour un exemple. Bref, c'est simple comme ci-dessous :
from joblib import dump , load
# save the model
dump ( clf , 'clf.joblib' )
# load the model
clf = load ( 'clf.joblib' )
On sait qu’il est difficile de sauvegarder les modèles de réseaux neuronaux. Vérifiez les numéros 328 et 88 pour une solution de contournement temporaire.
Train rapide avec SUOD
Formation et prédiction rapides : il est possible de former et de prédire avec un grand nombre de modèles de détection dans PyOD en tirant parti du framework SUOD [50]. Voir le papier SUOD et l'exemple SUOD.
from pyod . models . suod import SUOD
# initialized a group of outlier detectors for acceleration
detector_list = [ LOF ( n_neighbors = 15 ), LOF ( n_neighbors = 20 ),
LOF ( n_neighbors = 25 ), LOF ( n_neighbors = 35 ),
COPOD (), IForest ( n_estimators = 100 ),
IForest ( n_estimators = 200 )]
# decide the number of parallel process, and the combination method
# then clf can be used as any outlier detection model
clf = SUOD ( base_estimators = detector_list , n_jobs = 2 , combination = 'average' ,
verbose = False )
Seuil des scores aberrants
Une approche davantage basée sur les données peut être adoptée lors de la définition du niveau de contamination. En utilisant une méthode de seuillage, la supposition d’une valeur arbitraire peut être remplacée par des techniques testées pour séparer les valeurs inlieres et aberrantes. Reportez-vous à PyThresh pour un examen plus approfondi du seuillage.
from pyod . models . knn import KNN
from pyod . models . thresholds import FILTER
# Set the outlier detection and thresholding methods
clf = KNN ( contamination = FILTER ())
Voir les méthodes de seuillage prises en charge dans seuillage.
Algorithmes implémentés
La boîte à outils PyOD se compose de quatre groupes fonctionnels principaux :
(i) Algorithmes de détection individuels :
| Taper | Abréviation | Algorithme | Année | Réf |
|---|
| Probabiliste | ECOD | Détection de valeurs aberrantes non supervisée à l'aide de fonctions de distribution cumulative empiriques | 2022 | [28] |
| Probabiliste | À L'ABORD | Détection des valeurs aberrantes basée sur l'angle | 2008 | [22] |
| Probabiliste | RapideABOD | Détection rapide des valeurs aberrantes basée sur l'angle par approximation | 2008 | [22] |
| Probabiliste | COPODE | COPOD : Détection des valeurs aberrantes basée sur la copule | 2020 | [27] |
| Probabiliste | FOU | Écart médian absolu (MAD) | 1993 | [19] |
| Probabiliste | SOS | Sélection de valeurs aberrantes stochastiques | 2012 | [20] |
| Probabiliste | QMCD | Détection des valeurs aberrantes de divergence quasi-Monte Carlo | 2001 | [11] |
| Probabiliste | KDE | Détection des valeurs aberrantes avec les fonctions de densité du noyau | 2007 | [24] |
| Probabiliste | Échantillonnage | Détection rapide des valeurs aberrantes basée sur la distance par échantillonnage | 2013 | [42] |
| Probabiliste | GMM | Modélisation probabiliste de mélanges pour l'analyse des valeurs aberrantes | | [1] [Ch.2] |
| Modèle linéaire | APC | Analyse en composantes principales (la somme des distances projetées pondérées par rapport aux hyperplans vectoriels propres) | 2003 | [41] |
| Modèle linéaire | KPCA | Analyse en composantes principales du noyau | 2007 | [18] |
| Modèle linéaire | MCD | Déterminant de covariance minimale (utiliser les distances de Mahalanobis comme scores aberrants) | 1999 | [16] [37] |
| Modèle linéaire | CD | Utilisez la distance de Cook pour la détection des valeurs aberrantes | 1977 | [10] |
| Modèle linéaire | OCSVM | Machines à vecteurs de support à une classe | 2001 | [40] |
| Modèle linéaire | LMDD | Détection des valeurs aberrantes basée sur les écarts (LMDD) | 1996 | [6] |
| Basé sur la proximité | LOF | Facteur de valeur aberrante locale | 2000 | [8] |
| Basé sur la proximité | COF | Facteur aberrant basé sur la connectivité | 2002 | [43] |
| Basé sur la proximité | (incrémental) COF | Facteur aberrant basé sur une connectivité efficace en mémoire (plus lent mais réduit la complexité du stockage) | 2002 | [43] |
| Basé sur la proximité | CBLOF | Facteur de valeurs aberrantes locales basé sur le clustering | 2003 | [17] |
| Basé sur la proximité | LOCAL | LOCI : détection rapide des valeurs aberrantes à l'aide de l'intégrale de corrélation locale | 2003 | [33] |
| Basé sur la proximité | HBOS | Score aberrant basé sur l'histogramme | 2012 | [12] |
| Basé sur la proximité | kNN | k Voisins les plus proches (utilisez la distance jusqu'au kème voisin le plus proche comme score aberrant) | 2000 | [36] |
| Basé sur la proximité | Moy.KNN | kNN moyen (utiliser la distance moyenne jusqu'aux k voisins les plus proches comme score aberrant) | 2002 | [5] |
| Basé sur la proximité | MedKNN | kNN médian (utiliser la distance médiane jusqu'aux k voisins les plus proches comme score aberrant) | 2002 | [5] |
| Basé sur la proximité | GAZON | Détection des valeurs aberrantes dans le sous-espace | 2009 | [23] |
| Basé sur la proximité | TIGE | Détection des valeurs aberrantes basée sur la rotation | 2020 | [4] |
| Ensembles aberrants | IForêt | Forêt d'isolement | 2008 | [29] |
| Ensembles aberrants | INNE | Détection d'anomalies basée sur l'isolement à l'aide des ensembles de voisins les plus proches | 2018 | [7] |
| Ensembles aberrants | DIF | Forêt d'isolement profond pour la détection des anomalies | 2023 | [45] |
| Ensembles aberrants | Facebook | Ensachage des fonctionnalités | 2005 | [25] |
| Ensembles aberrants | LSCP | LSCP : combinaison localement sélective d'ensembles aberrants parallèles | 2019 | [49] |
| Ensembles aberrants | XGBOD | Détection des valeurs aberrantes basée sur un boosting extrême (supervisé) | 2018 | [48] |
| Ensembles aberrants | LODA | Détecteur d'anomalies en ligne léger | 2016 | [34] |
| Ensembles aberrants | SUOD | SUOD : accélération de la détection des valeurs aberrantes hétérogènes non supervisées à grande échelle (accélération) | 2021 | [50] |
| Réseaux de neurones | Encodeur automatique | AutoEncoder entièrement connecté (utiliser l’erreur de reconstruction comme score aberrant) | | [1] [Ch.3] |
| Réseaux de neurones | VAE | AutoEncoder variationnel (utiliser l'erreur de reconstruction comme score aberrant) | 2013 | [21] |
| Réseaux de neurones | Bêta-VAE | AutoEncoder variationnel (tous les termes de perte personnalisés en faisant varier le gamma et la capacité) | 2018 | [9] |
| Réseaux de neurones | SO_GAAL | Apprentissage actif contradictoire génératif à objectif unique | 2019 | [30] |
| Réseaux de neurones | MO_GAAL | Apprentissage actif contradictoire génératif à objectifs multiples | 2019 | [30] |
| Réseaux de neurones | DeepSVDD | Classification approfondie d'une classe | 2018 | [38] |
| Réseaux de neurones | AnoGAN | Détection d'anomalies avec des réseaux adverses génératifs | 2017 | [39] |
| Réseaux de neurones | ALAD | Détection des anomalies apprises de manière contradictoire | 2018 | [47] |
| Réseaux de neurones | AE1SVM | Machine à vecteurs de support à une classe basée sur un encodeur automatique | 2019 | [31] |
| Réseaux de neurones | DevNet | Détection d'anomalies profondes avec des réseaux de déviation | 2019 | [32] |
| Basé sur un graphique | Graphique R | Détection des valeurs aberrantes par R-graph | 2017 | [46] |
| Basé sur un graphique | LUNAIRE | LUNAR : unifier les méthodes de détection des valeurs aberrantes locales via des réseaux de neurones graphiques | 2022 | [13] |
(ii) Cadres de combinaison d'ensembles de valeurs aberrantes et de détecteurs de valeurs aberrantes :
| Taper | Abréviation | Algorithme | Année | Réf |
|---|
| Ensembles aberrants | Facebook | Ensachage des fonctionnalités | 2005 | [25] |
| Ensembles aberrants | LSCP | LSCP : combinaison localement sélective d'ensembles aberrants parallèles | 2019 | [49] |
| Ensembles aberrants | XGBOD | Détection des valeurs aberrantes basée sur un boosting extrême (supervisé) | 2018 | [48] |
| Ensembles aberrants | LODA | Détecteur d'anomalies en ligne léger | 2016 | [34] |
| Ensembles aberrants | SUOD | SUOD : accélération de la détection des valeurs aberrantes hétérogènes non supervisées à grande échelle (accélération) | 2021 | [50] |
| Ensembles aberrants | INNE | Détection d'anomalies basée sur l'isolement à l'aide des ensembles de voisins les plus proches | 2018 | [7] |
| Combinaison | Moyenne | Combinaison simple en faisant la moyenne des scores | 2015 | [2] |
| Combinaison | Moyenne pondérée | Combinaison simple en faisant la moyenne des scores avec les poids des détecteurs | 2015 | [2] |
| Combinaison | Maximisation | Combinaison simple en prenant le maximum de scores | 2015 | [2] |
| Combinaison | AOM | Moyenne du maximum | 2015 | [2] |
| Combinaison | MOA | Maximisation de la moyenne | 2015 | [2] |
| Combinaison | Médian | Combinaison simple en prenant la médiane des scores | 2015 | [2] |
| Combinaison | vote majoritaire | Combinaison simple en prenant le vote majoritaire des labels (des poids peuvent être utilisés) | 2015 | [2] |
(iii) Fonctions utilitaires :
| Taper | Nom | Fonction | Documentation |
|---|
| Données | générer_données | Génération de données synthétisées ; les données normales sont générées par une gaussienne multivariée et les valeurs aberrantes sont générées par une distribution uniforme | générer_données |
| Données | generate_data_clusters | Génération de données synthétisées en clusters ; des modèles de données plus complexes peuvent être créés avec plusieurs clusters | generate_data_clusters |
| Statistique | wpearsonr | Calculer la corrélation de Pearson pondérée de deux échantillons | wpearsonr |
| Utilitaire | get_label_n | Transformez les scores aberrants bruts en étiquettes binaires en attribuant 1 aux n premiers scores aberrants | get_label_n |
| Utilitaire | précision_n_scores | calculer la précision au rang n | précision_n_scores |
Démarrage rapide pour la détection des valeurs aberrantes
PyOD a été bien reconnu par la communauté d'apprentissage automatique avec quelques articles et didacticiels en vedette.
Analytics Vidhya : un didacticiel génial pour apprendre la détection des valeurs aberrantes en Python à l'aide de la bibliothèque PyOD
KDnuggets : Visualisation intuitive des méthodes de détection des valeurs aberrantes, un aperçu des méthodes de détection des valeurs aberrantes de PyOD
Vers la science des données : la détection d'anomalies pour les nuls
"examples/knn_example.py" démontre l'API de base de l'utilisation du détecteur kNN. Il est à noter que les API de tous les autres algorithmes sont cohérentes/similaires .
Des instructions plus détaillées pour exécuter des exemples peuvent être trouvées dans le répertoire des exemples.
Initialisez un détecteur kNN, ajustez le modèle et effectuez la prédiction.
from pyod . models . knn import KNN # kNN detector
# train kNN detector
clf_name = 'KNN'
clf = KNN ()
clf . fit ( X_train )
# get the prediction label and outlier scores of the training data
y_train_pred = clf . labels_ # binary labels (0: inliers, 1: outliers)
y_train_scores = clf . decision_scores_ # raw outlier scores
# get the prediction on the test data
y_test_pred = clf . predict ( X_test ) # outlier labels (0 or 1)
y_test_scores = clf . decision_function ( X_test ) # outlier scores
# it is possible to get the prediction confidence as well
y_test_pred , y_test_pred_confidence = clf . predict ( X_test , return_confidence = True ) # outlier labels (0 or 1) and confidence in the range of [0,1]
Évaluez la prédiction par ROC et Precision @ Rank n (p@n).
from pyod . utils . data import evaluate_print
# evaluate and print the results
print ( " n On Training Data:" )
evaluate_print ( clf_name , y_train , y_train_scores )
print ( " n On Test Data:" )
evaluate_print ( clf_name , y_test , y_test_scores )
Voir un exemple de sortie et de visualisation.
On Training Data :
KNN ROC : 1.0 , precision @ rank n : 1.0
On Test Data :
KNN ROC : 0.9989 , precision @ rank n : 0.9
visualize ( clf_name , X_train , y_train , X_test , y_test , y_train_pred ,
y_test_pred , show_figure = True , save_figure = False )
Visualisation (knn_figure) :
Référence
| [1] | (1, 2) Aggarwal, CC, 2015. Analyse des valeurs aberrantes. Dans Exploration de données (pp. 237-263). Springer, Cham. |
| [2] | (1, 2, 3, 4, 5, 6, 7) Aggarwal, CC et Sathe, S., 2015. Fondements théoriques et algorithmes pour les ensembles aberrants. Bulletin d'exploration ACM SIGKDD , 17(1), pp.24-47. |
| [3] | Aggarwal, CC et Sathe, S., 2017. Ensembles aberrants : une introduction. Springer. |
| [4] | Almardeny, Y., Boujnah, N. et Cleary, F., 2020. Une nouvelle méthode de détection des valeurs aberrantes pour les données multivariées. Transactions IEEE sur l'ingénierie des connaissances et des données . |
| [5] | (1, 2) Angiulli, F. et Pizzuti, C., 2002, août. Détection rapide des valeurs aberrantes dans les espaces de grande dimension. Dans Conférence européenne sur les principes de l'exploration de données et de la découverte des connaissances, pp. 15-27. |
| [6] | Arning, A., Agrawal, R. et Raghavan, P., 1996, août. Une méthode linéaire pour la détection des écarts dans les grandes bases de données. Dans KDD (Vol. 1141, n° 50, pp. 972-981). |
| [7] | (1, 2) Bandaragoda, TR, Ting, KM, Albrecht, D., Liu, FT, Zhu, Y. et Wells, JR, 2018, Détection d'anomalies basée sur l'isolement à l'aide d'ensembles de voisins les plus proches. Intelligence informatique , 34(4), pages 968 à 998. |
| [8] | Breunig, MM, Kriegel, HP, Ng, RT et Sander, J., 2000, mai. LOF : identification des valeurs aberrantes locales basées sur la densité. Enregistrement ACM Sigmod , 29(2), pages 93-104. |
| [9] | Burgess, Christopher P. et coll. "Comprendre le démêlage en bêta-VAE." Préimpression arXiv arXiv:1804.03599 (2018). |
| [10] | Cook, RD, 1977. Détection d'observations influentes dans la régression linéaire. Technométrie, 19(1), pp.15-18. |
| [11] | Fang, KT et Ma, CX, 2001. Écart L2 global de l'échantillonnage aléatoire, de l'hypercube latin et des plans uniformes. Journal de complexité, 17(4), pp.608-624. |
| [12] | Goldstein, M. et Dengel, A., 2012. Score aberrant basé sur l'histogramme (hbos) : un algorithme rapide de détection d'anomalies non supervisé. Dans KI-2012 : affiche et piste de démonstration , pp.59-63. |
| [13] | Goodge, A., Hooi, B., Ng, SK et Ng, WS, juin 2022. Lunar : unifier les méthodes de détection des valeurs aberrantes locales via des réseaux de neurones graphiques. Dans les actes de la conférence AAAI sur l'intelligence artificielle. |
| [14] | Gopalan, P., Sharan, V. et Wieder, U., 2019. PIDForest : Détection d'anomalies via une identification partielle. Dans Avancées des systèmes de traitement de l'information neuronale, pp. 15783-15793. |
| [15] | Han, S., Hu, X., Huang, H., Jiang, M. et Zhao, Y., 2022. ADBench : Anomaly Detection Benchmark. Préimpression arXiv arXiv :2206.09426. |
| [16] | Hardin, J. et Rocke, DM, 2004. Détection des valeurs aberrantes dans le contexte de grappes multiples à l'aide de l'estimateur du déterminant de covariance minimale. Statistiques informatiques et analyse des données , 44(4), pp.625-638. |
| [17] | He, Z., Xu, X. et Deng, S., 2003. Découverte des valeurs aberrantes locales basées sur les clusters. Lettres de reconnaissance de formes , 24 (9-10), pp.1641-1650. |
| [18] | Hoffmann, H., 2007. Kernel PCA pour la détection de nouveauté. Reconnaissance de formes, 40(3), pp.863-874. |
| [19] | Iglewicz, B. et Hoaglin, DC, 1993. Comment détecter et gérer les valeurs aberrantes (Vol. 16). Asq Presse. |
| [20] | Janssens, JHM, Huszár, F., Postma, EO et van den Herik, HJ, 2012. Sélection de valeurs aberrantes stochastiques. Rapport technique TiCC TR 2012-001, Université de Tilburg, Centre de Tilburg pour la cognition et la communication, Tilburg, Pays-Bas. |
| [21] | Kingma, DP et Welling, M., 2013. Bayes variationnelles à codage automatique. Préimpression arXiv arXiv:1312.6114. |
| [22] | (1, 2) Kriegel, HP et Zimek, A., 2008, août. Détection des valeurs aberrantes basée sur l'angle dans les données de grande dimension. Dans KDD '08 , pp. 444-452. ACM. |
| [23] | Kriegel, HP, Kröger, P., Schubert, E. et Zimek, A., 2009, avril. Détection des valeurs aberrantes dans les sous-espaces à axes parallèles de données de grande dimension. Dans Conférence Pacifique-Asie sur la découverte des connaissances et l'exploration de données , pp. Springer, Berlin, Heidelberg. |
| [24] | Latecki, LJ, Lazarevic, A. et Pokrajac, D., juillet 2007. Détection des valeurs aberrantes avec des fonctions de densité de noyau. Dans l'atelier international sur l'apprentissage automatique et l'exploration de données dans la reconnaissance de formes (pp. 61-75). Springer, Berlin, Heidelberg. |
| [25] | (1, 2) Lazarevic, A. et Kumar, V., 2005, août. Fonctionnalité d'ensachage pour la détection des valeurs aberrantes. Dans KDD '05 . 2005. |
| [26] | Li, D., Chen, D., Jin, B., Shi, L., Goh, J. et Ng, SK, 2019, septembre. MAD-GAN : Détection d'anomalies multivariées pour les données de séries chronologiques avec des réseaux contradictoires génératifs. Dans Conférence internationale sur les réseaux de neurones artificiels (pp. 703-716). Springer, Cham. |
| [27] | Li, Z., Zhao, Y., Botta, N., Ionescu, C. et Hu, X. COPOD : Détection des valeurs aberrantes basée sur la copule. Conférence internationale de l'IEEE sur l'exploration de données (ICDM) , 2020. |
| [28] | Li, Z., Zhao, Y., Hu, X., Botta, N., Ionescu, C. et Chen, HG ECOD : Détection de valeurs aberrantes non supervisées à l'aide de fonctions de distribution cumulative empiriques. Transactions IEEE sur l'ingénierie des connaissances et des données (TKDE) , 2022. |
| [29] | Liu, FT, Ting, KM et Zhou, ZH, décembre 2008. Forêt d'isolement. Dans Conférence internationale sur l'exploration de données , pp. 413-422. IEEE. |
| [30] | (1, 2) Liu, Y., Li, Z., Zhou, C., Jiang, Y., Sun, J., Wang, M. et He, X., 2019. Apprentissage actif contradictoire génératif pour la détection des valeurs aberrantes non supervisées . Transactions IEEE sur l'ingénierie des connaissances et des données . |
| [31] | Nguyen, MN et Vien, NA, 2019. SVMS à une classe évolutifs et interprétables avec apprentissage en profondeur et fonctionnalités de fourier aléatoires. Dans Apprentissage automatique et découverte de connaissances dans les bases de données : Conférence européenne , ECML PKDD, 2018. |
| [32] | Pang, Guansong, Chunhua Shen et Anton Van Den Hengel. "Détection d'anomalies profondes avec des réseaux de déviation." Dans KDD , pp. 353-362. 2019. |
| [33] | Papadimitriou, S., Kitagawa, H., Gibbons, PB et Faloutsos, C., 2003, mars. LOCI : détection rapide des valeurs aberrantes à l'aide de l'intégrale de corrélation locale. Dans ICDE '03 , pp. 315-326. IEEE. |
| [34] | (1, 2) Pevný, T., 2016. Loda : Détecteur léger d'anomalies en ligne. Apprentissage automatique , 102(2), pages 275-304. |
| [35] | Perini, L., Vercruyssen, V., Davis, J. Quantification de la confiance des détecteurs d'anomalies dans leurs prédictions par exemples. Dans le cadre de la Conférence européenne conjointe sur l'apprentissage automatique et la découverte de connaissances dans les bases de données (ECML-PKDD) , 2020. |
| [36] | Ramaswamy, S., Rastogi, R. et Shim, K., 2000, mai. Algorithmes efficaces pour extraire les valeurs aberrantes à partir de grands ensembles de données. Enregistrement ACM Sigmod , 29(2), pages 427-438. |
| [37] | Rousseeuw, PJ et Driessen, KV, 1999. Un algorithme rapide pour l'estimateur du déterminant de covariance minimale. Technométrie , 41(3), pp.212-223. |
| [38] | Ruff, L., Vandermeulen, R., Goernitz, N., Deecke, L., Siddiqui, SA, Binder, A., Müller, E. et Kloft, M., juillet 2018. Classification profonde d'une classe. Dans Conférence internationale sur l'apprentissage automatique (pp. 4393-4402). PMLR. |
| [39] | Schlegl, T., Seeböck, P., Waldstein, SM, Schmidt-Erfurth, U. et Langs, G., 2017, juin. Détection d'anomalies non supervisée avec des réseaux contradictoires génératifs pour guider la découverte de marqueurs. Dans Conférence internationale sur le traitement de l'information en imagerie médicale (pp. 146-157). Springer, Cham. |
| [40] | Scholkopf, B., Platt, JC, Shawe-Taylor, J., Smola, AJ et Williamson, RC, 2001. Estimation du support d'une distribution de grande dimension. Calcul neuronal , 13(7), pages 1443-1471. |
| [41] | Shyu, ML, Chen, SC, Sarinnapakorn, K. et Chang, L., 2003. Un nouveau schéma de détection d'anomalies basé sur un classificateur de composants principaux. MIAMI UNIV CORAL GABLES FL DÉPT DE GÉNIE ÉLECTRIQUE ET INFORMATIQUE . |
| [42] | Sugiyama, M. et Borgwardt, K., 2013. Détection rapide des valeurs aberrantes basée sur la distance par échantillonnage. Progrès dans les systèmes de traitement de l'information neuronale, 26. |
| [43] | (1, 2) Tang, J., Chen, Z., Fu, AWC et Cheung, DW, 2002, mai. Amélioration de l'efficacité de la détection des valeurs aberrantes pour les modèles de faible densité. Dans Conférence Pacifique-Asie sur la découverte des connaissances et l'exploration de données , pp. 535-548. Springer, Berlin, Heidelberg. |
| [44] | Wang, X., Du, Y., Lin, S., Cui, P., Shen, Y. et Yang, Y., 2019. adVAE : un auto-encodeur variationnel auto-adversaire avec des connaissances préalables sur les anomalies gaussiennes pour la détection des anomalies. Systèmes basés sur la connaissance . |
| [45] | Xu, H., Pang, G., Wang, Y., Wang, Y., 2023. Forêt d'isolement profond pour la détection d'anomalies. Transactions IEEE sur l'ingénierie des connaissances et des données . |
| [46] | You, C., Robinson, DP et Vidal, R., 2017. Détection de valeurs aberrantes basée sur l'auto-représentation prouvable dans une union de sous-espaces. Dans Actes de la conférence IEEE sur la vision par ordinateur et la reconnaissance de formes. |
| [47] | Zenati, H., Romain, M., Foo, CS, Lecouat, B. et Chandrasekhar, V., 2018, novembre. Détection des anomalies apprises de manière contradictoire. En 2018, conférence internationale IEEE sur l'exploration de données (ICDM) (pp. 727-736). IEEE. |
| [48] | (1, 2) Zhao, Y. et Hryniewicki, MK XGBOD : Amélioration de la détection supervisée des valeurs aberrantes grâce à l'apprentissage des représentations non supervisé. Conférence conjointe internationale de l'IEEE sur les réseaux de neurones , 2018. |
| [49] | (1, 2) Zhao, Y., Nasrullah, Z., Hryniewicki, MK et Li, Z., 2019, mai. LSCP : combinaison localement sélective dans des ensembles aberrants parallèles. Dans Actes de la Conférence internationale SIAM 2019 sur l'exploration de données (SDM) , pp. 585-593. Société de mathématiques industrielles et appliquées. |
| [50] | (1, 2, 3, 4) Zhao, Y., Hu, X., Cheng, C., Wang, C., Wan, C., Wang, W., Yang, J., Bai, H., Li , Z., C. Xiao, Y. Wang, Z. Qiao, J. Sun et L. Akoglu (2021). SUOD : accélération de la détection des valeurs aberrantes hétérogènes non supervisées à grande échelle. Conférence sur l'apprentissage automatique et les systèmes (MLSys) . |


