Accueil | Installation | Documents | Tutoriel | Développeurs
rodeo est une bibliothèque Python rapide qui utilise des numériques probabilistes pour résoudre des équations différentielles ordinaires (ODE). Autrement dit, la plupart des solveurs ODE (comme la méthode d'Euler) produisent une approximation déterministe de l'ODE sur une grille de tailles de pas
rodeo fournit une famille légère et extensible d'approximations d'un paradigme de filtrage bayésien non linéaire commun à de nombreux solveurs probabilistes (Tronarp et al (2018)). Cela commence par placer un processus gaussien avant sur la solution ODE et par le mettre à jour séquentiellement au fur et à mesure que le solveur parcourt la grille. rodeo est construit sur jax qui permet une compilation juste à temps et une auto-différenciation. L'API de jax est presque équivalente à celle de numpy .
rodeo fournit deux outils principaux : un pour approximer la solution ODE et l'autre pour l'inférence de paramètres. Pour le premier, nous fournissons :
solve : Implémentation d'un solveur ODE probabiliste qui utilise un paradigme de filtrage bayésien non linéaire.Pour ces derniers, nous fournissons les méthodes d’approximation de vraisemblance :
basic : Mise en œuvre d'une méthode d'approximation de vraisemblance de base (les détails peuvent être trouvés dans Wu et Lysy (2023)).fenrir : Implémentation de Fenrir (Tronarp et al (2022)).marginal_mcmc : implémentation MCMC de la méthode de Chkrebtii (Chkrebtii et al (2016)).dalton : Implémentation de notre approximation de vraisemblance ODE adaptative aux données (Wu et Lysy (2023)).Des exemples détaillés de leur utilisation peuvent être trouvés dans la section Documentation. Veuillez noter qu'il s'agit de la version jax uniquement de rodeo . Pour les anciennes versions utilisant divers autres backends, veuillez consulter ici.
Téléchargez le dépôt depuis GitHub, puis installez-le avec le script setup.cfg :
git clone https://github.com/mlysy/rodeo.git
cd rodeo
pip install . Veuillez d'abord accéder à readthedocs pour voir la documentation rendue pour les exemples suivants.
Un didacticiel de démarrage rapide sur la résolution d'un problème ODE simple.
Un exemple pour résoudre une ODE d’ordre supérieur.
Un exemple pour résoudre une ODE chaotique difficile.
Un exemple de problème d'inférence de paramètres où nous utilisons l'approximation de Laplace.
Dans cette procédure pas à pas, nous montrons à la fois comment résoudre une ODE avec notre solveur probabiliste et effectuer l'inférence de paramètres. Nous allons d’abord illustrer la configuration pour résoudre l’ODE. À cette fin, considérons le premier exemple d'ODE ordonné suivant (modèle FitzHugh-Nagumo ),
où la solution
Suite à la notation de (Wu et Lysy (2023)), on a
pour
import jax
import jax . numpy as jnp
import rodeo
def fitz_fun ( X , t , ** params ):
"FitzHugh-Nagumo ODE in rodeo format."
a , b , c = params [ "theta" ]
V , R = X [:, 0 ]
return jnp . array (
[[ c * ( V - V * V * V / 3 + R )],
[ - 1 / c * ( V - a + b * R )]]
)
def fitz_init ( x0 , theta ):
"FitzHugh-Nagumo initial values in rodeo format."
x0 = x0 [:, None ]
return jnp . hstack ([
x0 ,
fitz_fun ( X = x0 , t = 0. , theta = theta ),
jnp . zeros_like ( x0 )
])
W = jnp . array ([[[ 0. , 1. , 0. ]], [[ 0. , 1. , 0. ]]]) # LHS matrix of ODE
x0 = jnp . array ([ - 1. , 1. ]) # initial value for the ODE-IVP
theta = jnp . array ([ .2 , .2 , 3 ]) # ODE parameters
X0 = fitz_init ( x0 , theta ) # initial value in rodeo format
# Time interval on which a solution is sought.
t_min = 0.
t_max = 40.
# --- Define the prior process -------------------------------------------
n_vars = 2 # number of variables in the ODE
n_deriv = 3 # max number of derivatives
sigma = jnp . array ([ .1 ] * n_vars ) # IBM process scale factor
# --- data simulation ------------------------------------------------------
n_steps = 800 # number of evaluations steps
dt = ( t_max - t_min ) / n_steps # step size
# generate the Kalman parameters corresponding to the prior
prior_Q , prior_R = rodeo . prior . ibm_init (
dt = dt_sim ,
n_deriv = n_deriv ,
sigma = sigma
)
# Produce a Pseudo-RNG key
key = jax . random . PRNGKey ( 0 )
Xt , _ = rodeo . solve_mv (
key = key ,
# define ode
ode_fun = fitz_fun ,
ode_weight = W ,
ode_init = X0 ,
t_min = t_min ,
t_max = t_max ,
theta = theta , # ODE parameters added here
# solver parameters
n_steps = n_steps ,
interrogate = rodeo . interrogate . interrogate_kramer ,
prior_weight = prior_Q ,
prior_var = prior_R
) Nous comparons la solution du solveur à la solution déterministe fournie par odeint dans la bibliothèque scipy .
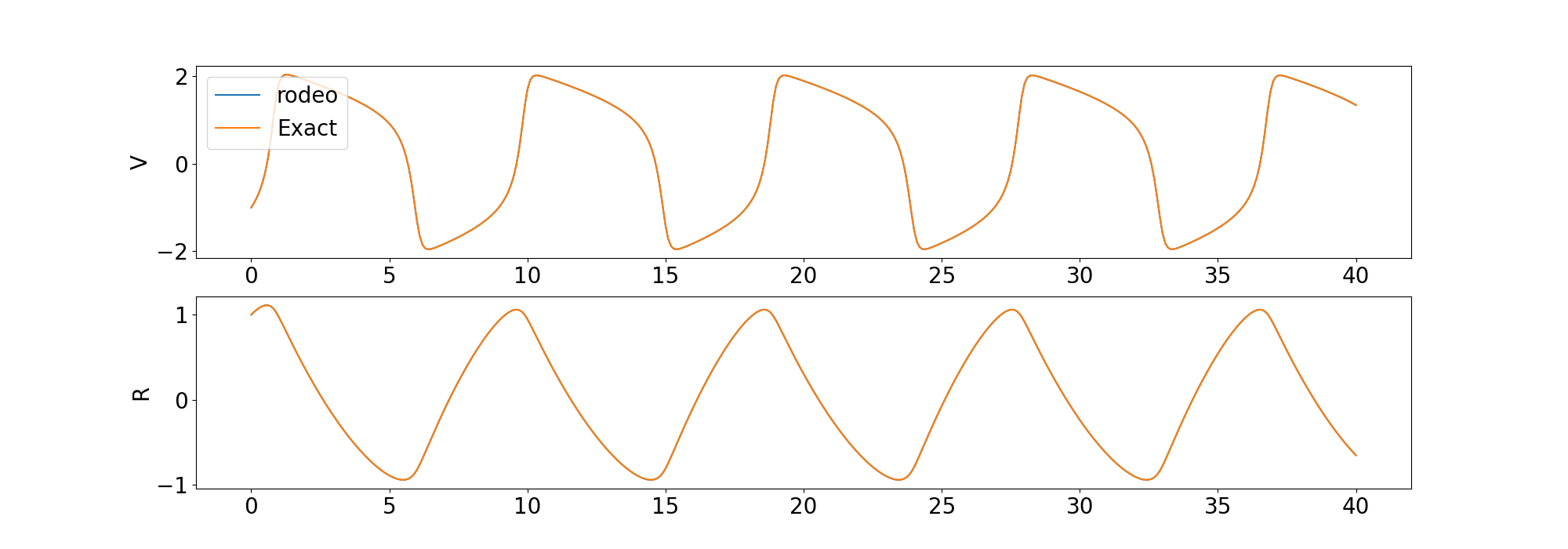
Nous incluons également des exemples pour résoudre une ODE d’ordre supérieur et une ODE chaotique.
Passons maintenant au problème d’inférence de paramètres. rodeo contient plusieurs méthodes d'approximation de vraisemblance résumées dans la section Description. Ici, nous utiliserons la méthode d’approximation basic de la vraisemblance. Supposons que les observations soient simulées via le modèle
où basic de la vraisemblance pour
def fitz_logprior ( upars ):
"Logprior on unconstrained model parameters."
n_theta = 5 # number of ODE + IV parameters
lpi = jax . scipy . stats . norm . logpdf (
x = upars [: n_theta ],
loc = 0. ,
scale = 10.
)
return jnp . sum ( lpi )
def fitz_loglik ( obs_data , ode_data , ** params ):
"""
Loglikelihood for measurement model.
Args:
obs_data (ndarray(n_obs, n_vars)): Observations data.
ode_data (ndarray(n_obs, n_vars, n_deriv)): ODE solution.
"""
ll = jax . scipy . stats . norm . logpdf (
x = obs_data ,
loc = ode_data [:, :, 0 ],
scale = 0.005
)
return jnp . sum ( ll )
def constrain_pars ( upars , dt ):
"""
Convert unconstrained optimization parameters into rodeo inputs.
Args:
upars : Parameters vector on unconstrainted scale.
dt : Discretization grid size.
Returns:
tuple with elements:
- theta : ODE parameters.
- X0 : Initial values in rodeo format.
- Q, R : Prior matrices.
"""
theta = jnp . exp ( upars [: 3 ])
x0 = upars [ 3 : 5 ]
X0 = fitz_init ( x0 , theta )
sigma = upars [ 5 :]
Q , R = rodeo . prior . ibm_init (
dt = dt ,
n_deriv = n_deriv ,
sigma = sigma
)
return theta , X0 , Q , R
def neglogpost_basic ( upars ):
"Negative logposterior for basic approximation."
# solve ODE
theta , X0 , prior_Q , prior_R = constrain_pars ( upars , dt_sim )
# basic loglikelihood
ll = rodeo . inference . basic (
key = key ,
# ode specification
ode_fun = fitz_fun ,
ode_weight = W ,
ode_init = X0 ,
t_min = t_min ,
t_max = t_max ,
theta = theta ,
# solver parameters
n_steps = n_steps ,
interrogate = rodeo . interrogate . interrogate_kramer ,
prior_weight = prior_Q ,
prior_var = prior_R ,
# observations
obs_data = obs_data ,
obs_times = obs_times ,
obs_loglik = fitz_loglik
)
return - ( ll + fitz_logprior ( upars )) Ceci est un exemple de base pour démontrer l’utilisation. Nous suggérons des approximations de vraisemblance plus sophistiquées qui propagent l'incertitude de la solution à l'approximation de vraisemblance telles que fenrir , marginal_mcmc et dalton . Veuillez vous référer au didacticiel d'inférence de paramètres pour plus de détails.
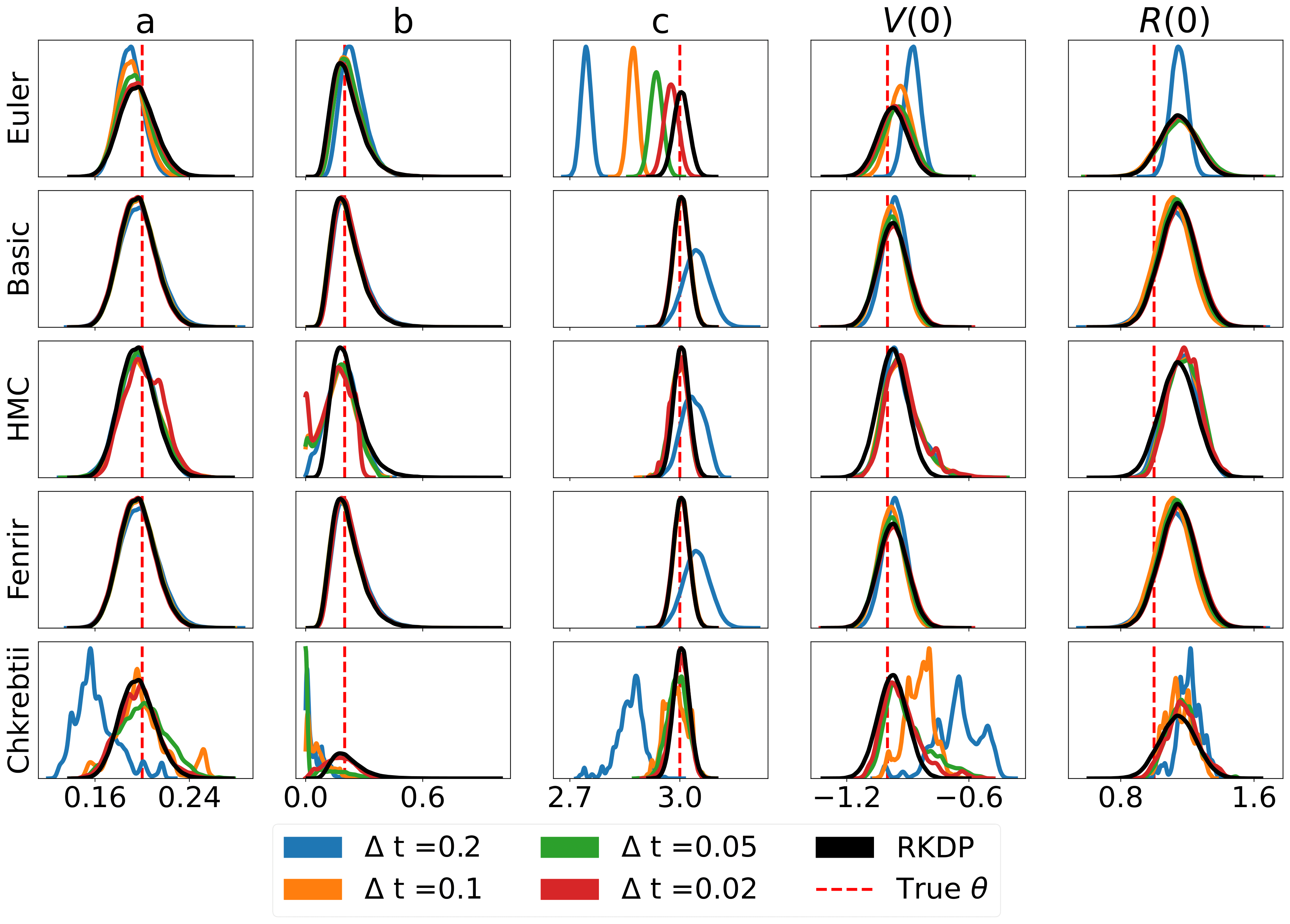
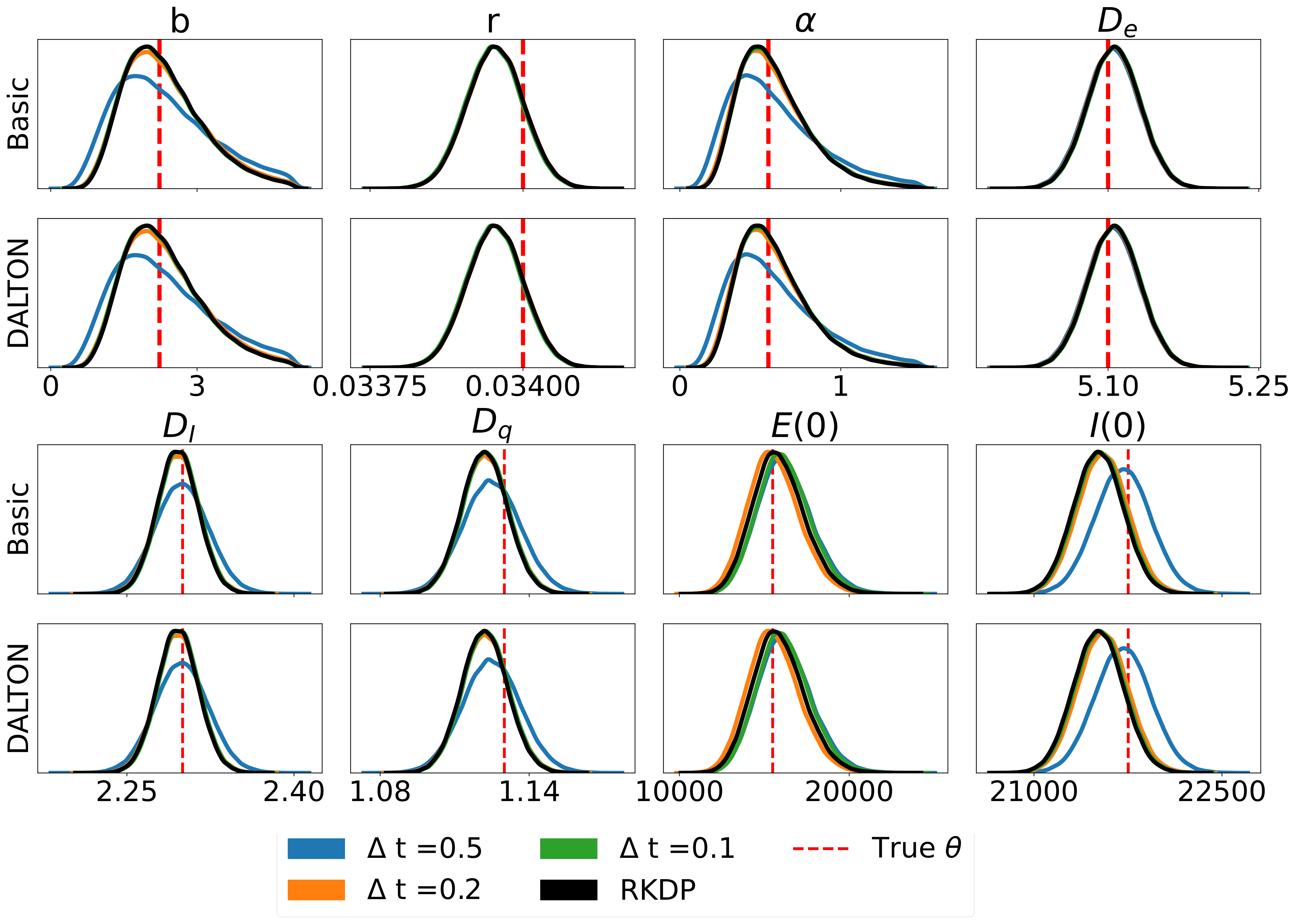
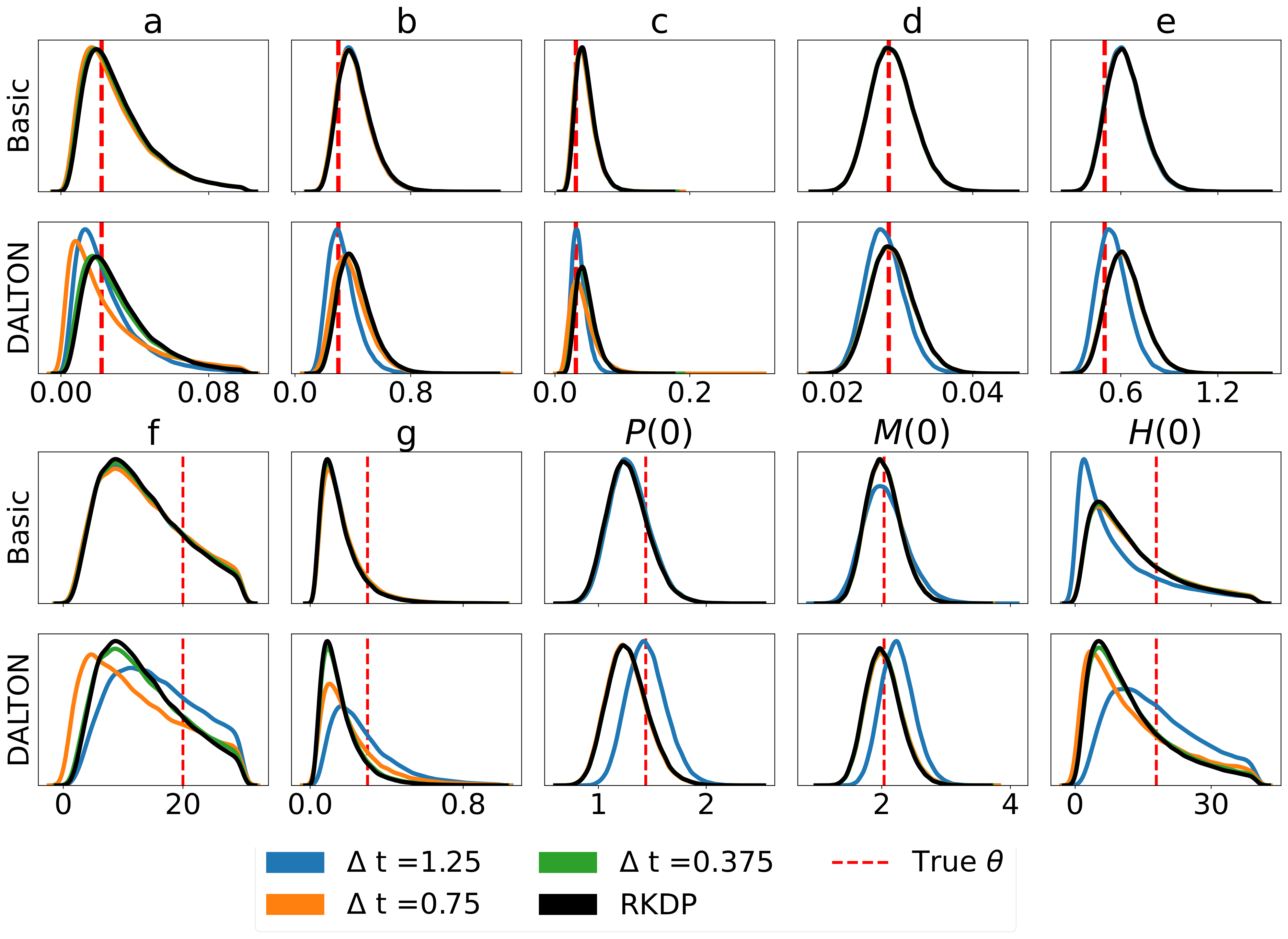
Voici quelques résultats produits par diverses approximations de vraisemblance trouvées dans le rodéo de /examples/ :
Les tests unitaires peuvent être exécutés via les commandes suivantes :
cd tests
python -m unittest discover -v Ou installez tox , puis depuis rodeo entrez la ligne de commande : tox .
La documentation HTML peut être compilée à partir du dossier racine :
pip install .[docs]
cd docs
make html Cela créera la documentation dans docs/build .