Awesome-latex-drawing est une collection de plus de 30 exemples de dessins académiques pour l'utilisation de LaTeX, y compris les réseaux bayésiens, le traçage de fonctions, les modèles graphiques, la structure tensorielle et les cadres techniques.
LaTeX est un système de composition de haute qualité disponible sous forme de logiciel libre, largement utilisé ces dernières années pour créer des graphiques académiques. Sa popularité vient de sa capacité à gérer des illustrations complexes avec des symboles spéciaux et des équations mathématiques, ce qui le rend idéal pour dessiner des graphiques détaillés dans le cadre de la recherche.
Ce projet présente plusieurs graphiques créés à l'aide de LaTeX, avec des exemples faciles à suivre sur Overleaf, une plateforme LaTeX en ligne populaire. Si vous êtes intéressé, n'hésitez pas à explorer et à reproduire nos exemples sur Overleaf sur overleaf.com.
pgfplots tikz pour la structure matricielle tikz-3dplot pour la structure tensorielle Vous recherchez de bons exemples de dessins LaTeX ? Voici plus de 30 graphiques montrant comment dessiner dans LaTaX.
LaTeX fournit de puissants packages et outils spécifiques à un domaine, comme tikz pour permettre des modèles graphiques flexibles. Les réseaux bayésiens représentent une famille de modèles graphiques constitués de variables (généralement désignées par des nœuds) et de relations de dépendance (généralement désignées par des flèches). Heureusement, tikz dispose d'une bibliothèque spécifique pour dessiner des réseaux bayésiens et des graphiques à facteurs orientés.
Une autre boîte à outils en Python : https://docs.daft-pgm.org/en/latest/
Cet exemple est tiré de l'article suivant :
- Qibin Zhao, Liqing Zhang, Andrzej Cichocki (2015). Factorisation bayésienne CP de tenseurs incomplets avec détermination automatique des rangs. Transactions IEEE sur l'analyse de modèles et l'intelligence artificielle, 37(9) : 1751-1763.
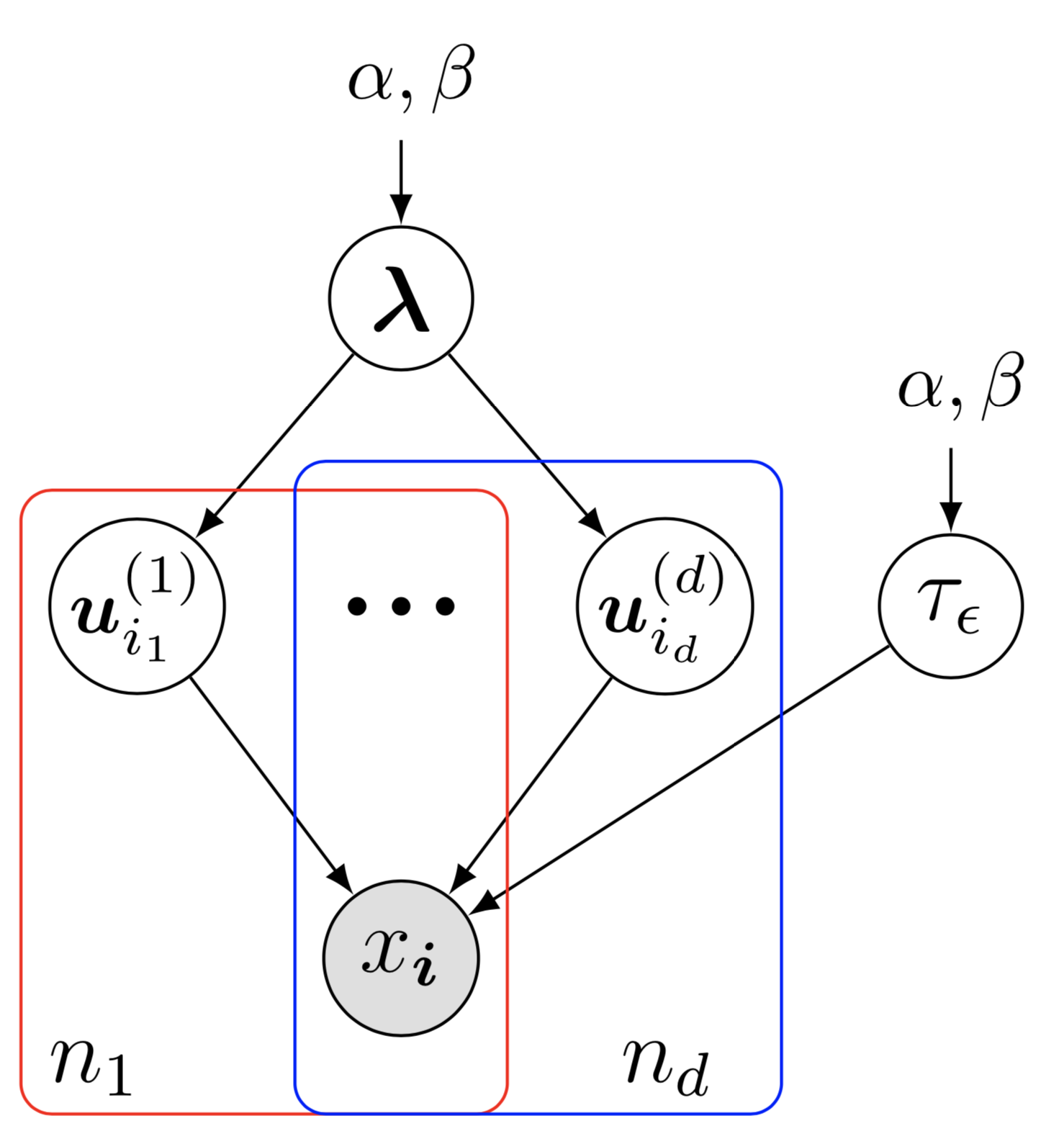 qui montre le modèle de réseau bayésien de factorisation bayésienne CP (BCPF). Pour dessiner cet exemple de réseau bayésien, il y a quelques préliminaires à suivre :
qui montre le modèle de réseau bayésien de factorisation bayésienne CP (BCPF). Pour dessiner cet exemple de réseau bayésien, il y a quelques préliminaires à suivre :preamble :documentclass comme standalone , par exemple documentclass[border = 0.1cm]{standalone} avec une bordure de 0,1 cm,tikz , c'est-à-dire usepackage{tikz} , et utilisez la bibliothèque tikz comme usetikzlibrary{bayesnet} qui est un outil important pour dessiner des réseaux bayésiens et des graphiques factoriels orientés,tikz en utilisant la commande tikzstyle{} ,usepackage{amsfonts, amsmath, amssymb} .body :begin{tikzpicture} end{tikzpicture} pour commencer à dessiner,node pour définir des nœuds et des zones de texte dans le réseau bayésien,path pour définir des flèches dans le réseau bayésien,plate pour définir les plaques dans le réseau bayésien.Veuillez cliquer sur l'image et consulter le code source.
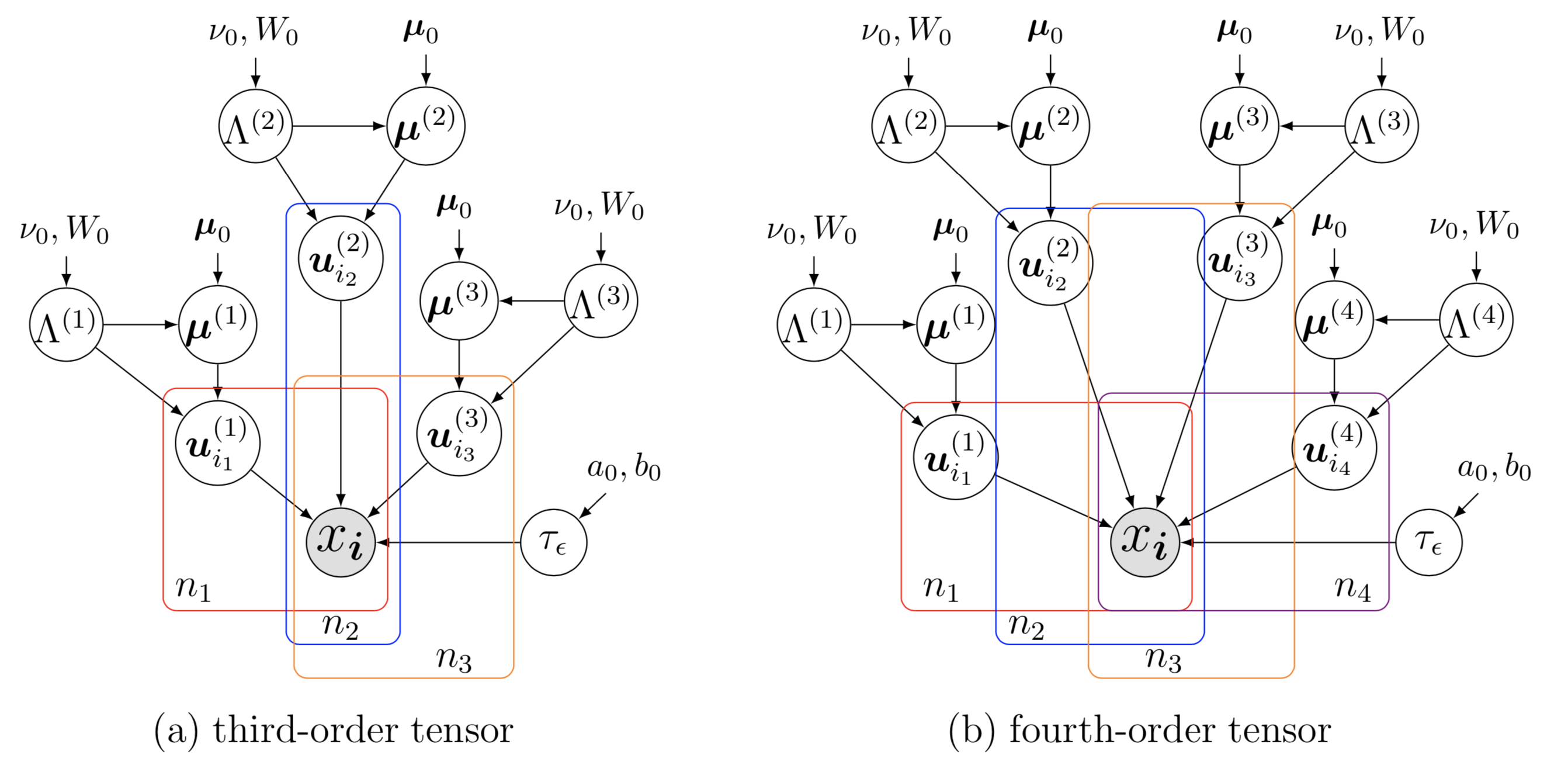
Cet exemple est tiré de l'article suivant :
Xinyu Chen, Zhaocheng He, Lijun Sun (2019). Une approche de décomposition tensorielle bayésienne pour l'imputation de données de trafic spatio-temporelles. Recherche sur les transports, partie C : Technologies émergentes, 98 : 73-84.
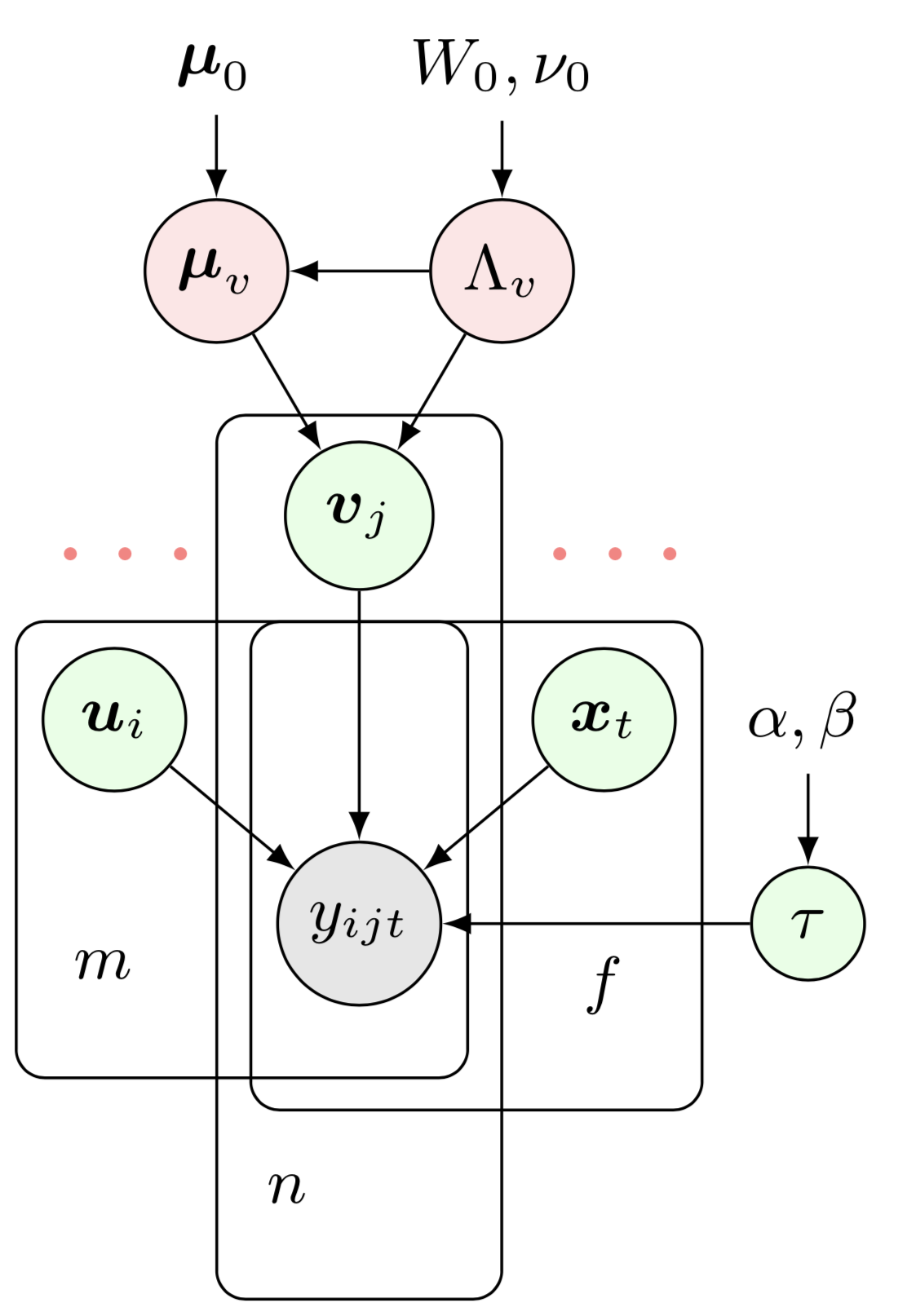 qui montre le réseau bayésien du modèle de factorisation bayésienne gaussienne CP (BGCP). Pour dessiner cet exemple de réseau bayésien, il y a quelques préliminaires à suivre :
qui montre le réseau bayésien du modèle de factorisation bayésienne gaussienne CP (BGCP). Pour dessiner cet exemple de réseau bayésien, il y a quelques préliminaires à suivre :preamble :documentclass comme standalone , par exemple documentclass[border = 0.1cm]{standalone} avec une bordure de 0,1 cm,tikz , c'est-à-dire usepackage{tikz} , et utilisez la bibliothèque tikz comme usetikzlibrary{bayesnet} qui est un outil important pour dessiner des réseaux bayésiens et des graphiques à facteurs orientés,tikz en utilisant la commande tikzstyle{} ,usepackage{amsmath, amsfonts, amssymb} .body :begin{tikzpicture} end{tikzpicture} pour commencer à dessiner,node pour définir des nœuds et des zones de texte dans le réseau bayésien,path pour définir des flèches dans le réseau bayésien,plate pour définir les plaques dans le réseau bayésien.Veuillez cliquer sur l'image et consulter le code source. Si vous êtes intéressé par le réseau bayésien original de BGCP dans le document, veuillez consulter BGCP.tex.
Cet exemple est tiré de l'article suivant :
Xinyu Chen, Zhaocheng He, Yixian Chen, Yuhuan Lu, Jiawei Wang (2019). Imputation des données de trafic manquantes et découverte de modèles avec un modèle de factorisation tenseur augmenté bayésien. Recherche sur les transports, partie C : technologies émergentes, 104 : 66-77.
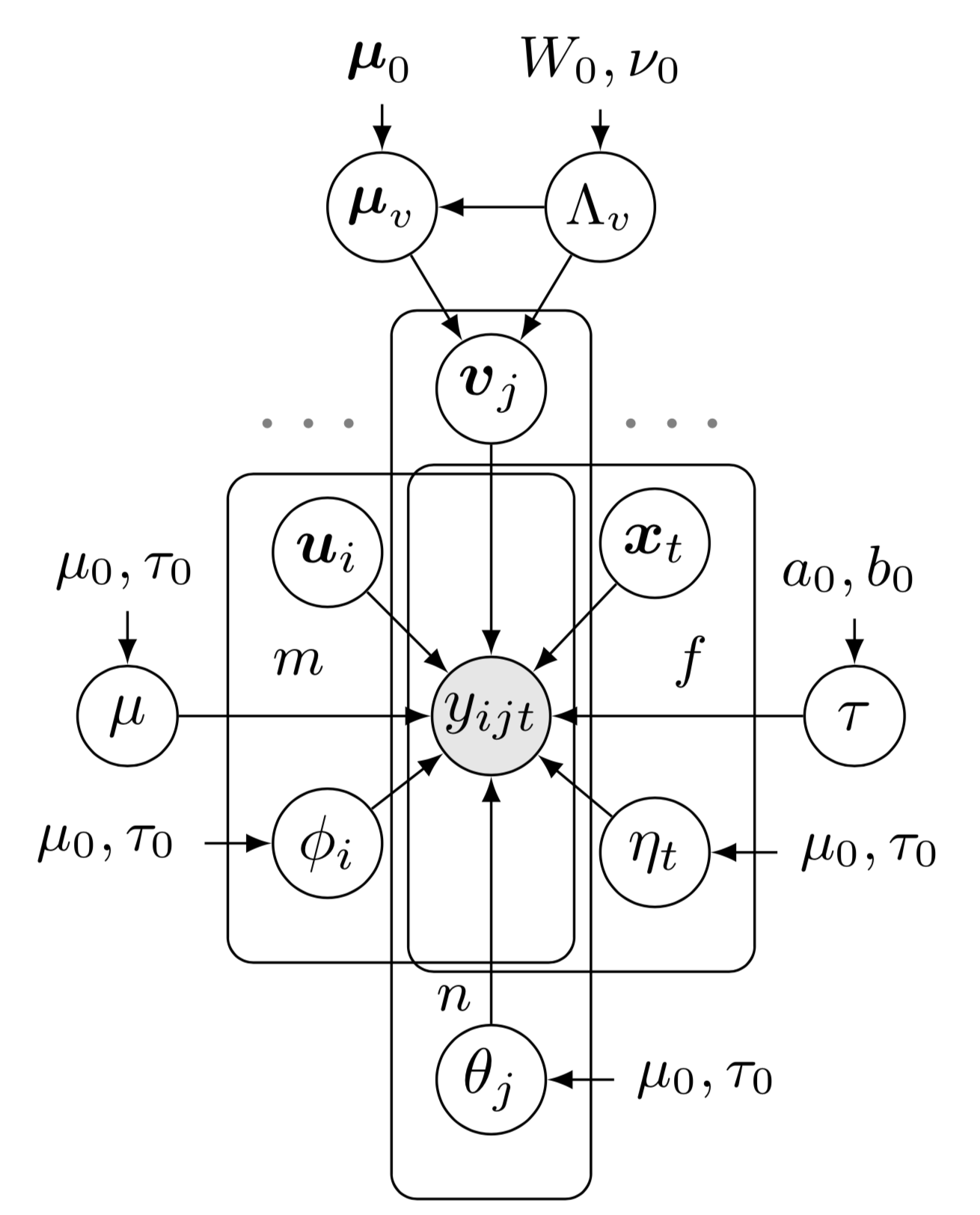 qui montre le réseau bayésien du modèle de factorisation tensorielle augmentée bayésienne (BATF). Pour dessiner cet exemple de réseau bayésien, il y a quelques préliminaires à suivre :
qui montre le réseau bayésien du modèle de factorisation tensorielle augmentée bayésienne (BATF). Pour dessiner cet exemple de réseau bayésien, il y a quelques préliminaires à suivre :preamble :documentclass comme standalone , par exemple documentclass[border = 0.1cm]{standalone} avec une bordure de 0,1 cm,tikz , c'est-à-dire usepackage{tikz} , et utilisez la bibliothèque tikz comme usetikzlibrary{bayesnet} qui est un outil important pour dessiner des réseaux bayésiens et des graphiques à facteurs orientés,tikz en utilisant la commande tikzstyle{} ,usepackage{amsmath, amsfonts, amssymb} .body :begin{tikzpicture} end{tikzpicture} pour commencer à dessiner,node pour définir des nœuds et des zones de texte dans le réseau bayésien,path pour définir des flèches dans le réseau bayésien,plate pour définir les plaques dans le réseau bayésien.Veuillez cliquer sur l'image et consulter le code source.
Cet exemple est tiré de l'article suivant :
Xinyu Chen, Lijun Sun (2021). Factorisation temporelle bayésienne pour la prédiction de séries chronologiques multidimensionnelles. Transactions IEEE sur l'analyse de modèles et l'intelligence artificielle, 44 (9) : 4659-4673.
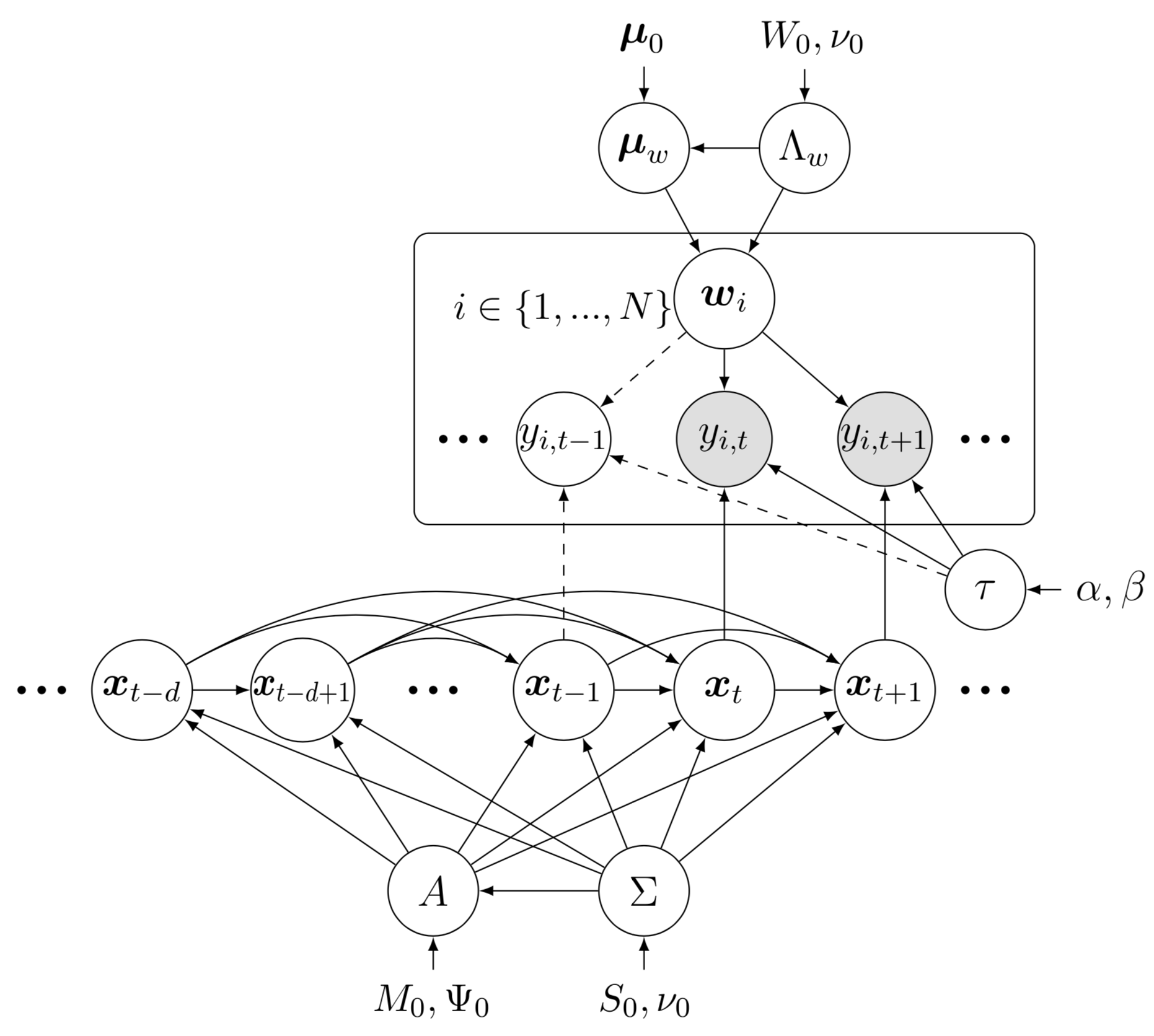 qui montre le réseau bayésien du modèle de factorisation matricielle temporelle bayésienne (BTMF). Pour dessiner cet exemple de réseau bayésien, il y a quelques préliminaires à suivre :
qui montre le réseau bayésien du modèle de factorisation matricielle temporelle bayésienne (BTMF). Pour dessiner cet exemple de réseau bayésien, il y a quelques préliminaires à suivre :preamble :documentclass comme standalone , par exemple documentclass[border = 0.1cm]{standalone} avec une bordure de 0,1 cm,tikz , c'est-à-dire usepackage{tikz} , et utilisez la bibliothèque tikz comme usetikzlibrary{bayesnet} qui est un outil important pour dessiner des réseaux bayésiens et des graphiques à facteurs orientés,tikz en utilisant la commande tikzstyle{} ,usepackage{amsmath, amsfonts, amssymb} .body :begin{tikzpicture} end{tikzpicture} pour commencer à dessiner,node pour définir des nœuds et des zones de texte dans le réseau bayésien,path pour définir des flèches dans le réseau bayésien,plate pour définir les plaques dans le réseau bayésien.Veuillez cliquer sur l'image et consulter le code source. Au lieu d'un processus autorégressif vectoriel multivarié sur des facteurs temporels, nous pouvons également utiliser un processus autorégressif univarié pour reconstruire BTMF. Le réseau Beyasian est disponible sur btmf_net.png, vous pouvez également consulter le code source btmf_net.tex.


Ces deux exemples montrent respectivement la matrice et le tenseur de séries chronologiques partiellement observés. Pour dessiner les deux exemples, nous pouvons suivre ces étapes :
codes preamble :
documentclass comme standalone ,tikz . codes body :
begin{tikzpicture} end{tikzpicture} pour commencer à dessiner,node pour définir des nœuds et des zones de texte dans le modèle graphique,path pour définir des flèches dans le modèle graphique. 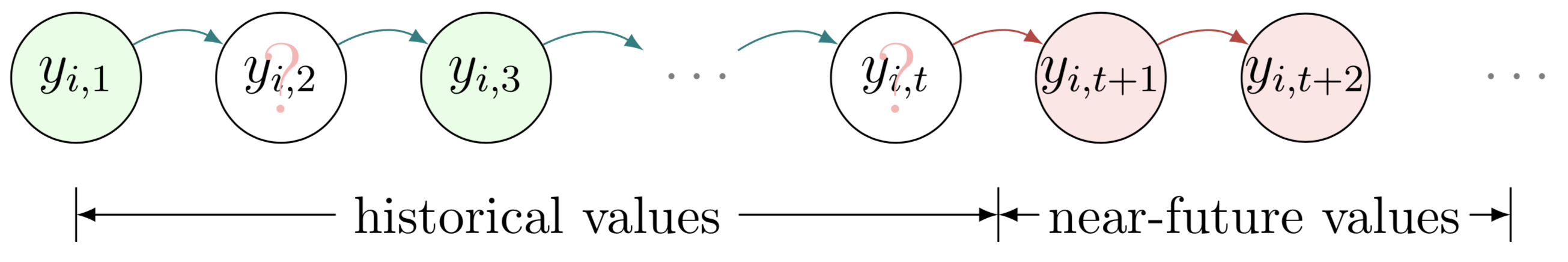
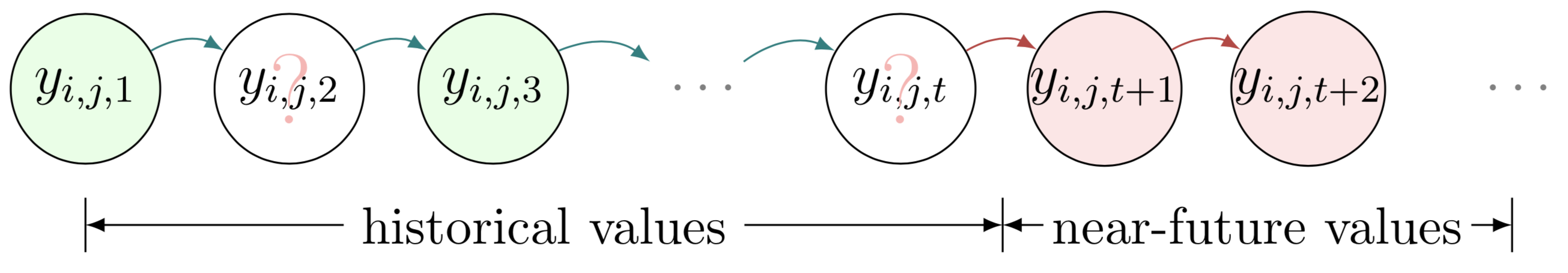
Ces deux exemples montrent la prédiction de séries chronologiques en présence de valeurs manquantes. Pour dessiner les deux exemples, nous pouvons suivre ces étapes :
codes preamble :
documentclass comme standalone ,tikz . codes body :
begin{tikzpicture} end{tikzpicture} pour commencer à dessiner,node pour définir des nœuds et des zones de texte dans le modèle graphique,path pour définir des flèches dans le modèle graphique. 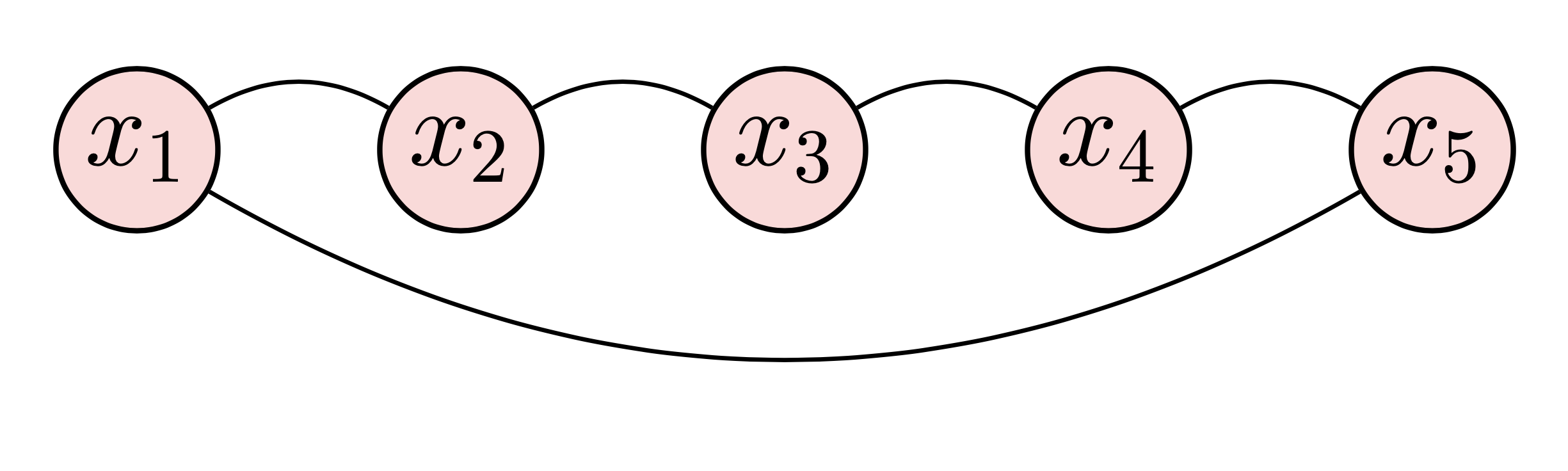
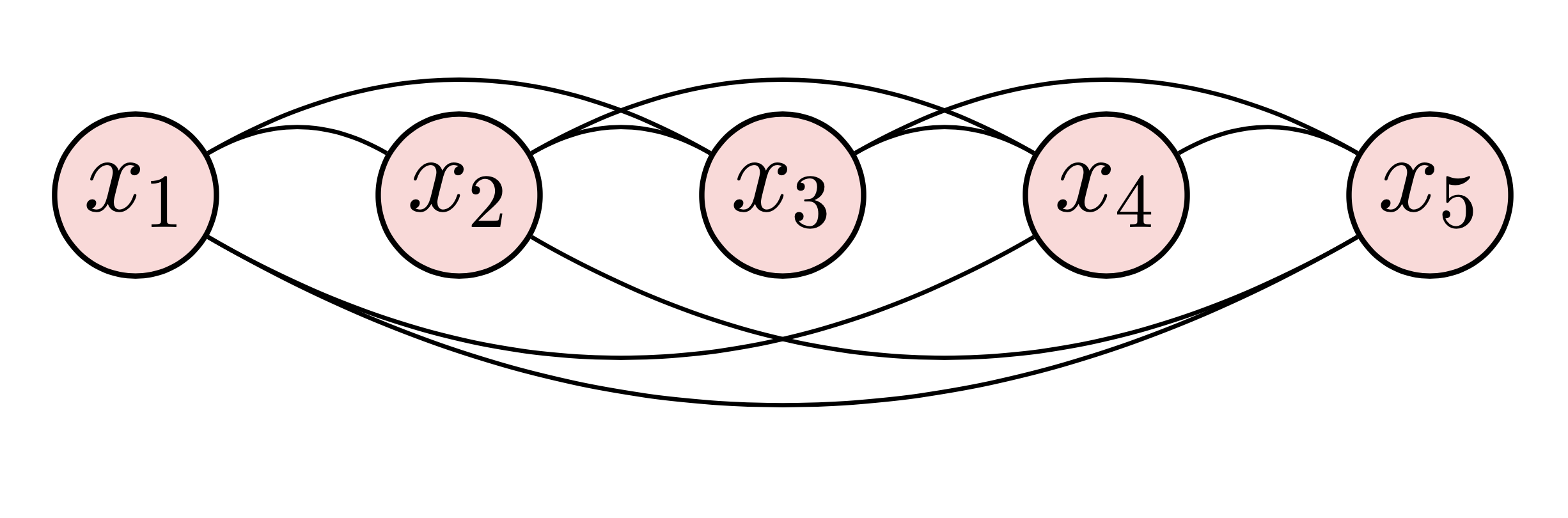
Ces deux exemples montrent les graphes non orientés et circulants sur les échantillons de données relationnelles avec certains degrés. Pour dessiner les deux exemples, nous pouvons suivre ces étapes :
codes preamble :
documentclass comme standalone ,tikz . codes body :
begin{tikzpicture} end{tikzpicture} pour commencer à dessiner,node pour définir les nœuds,path pour définir les flèches. 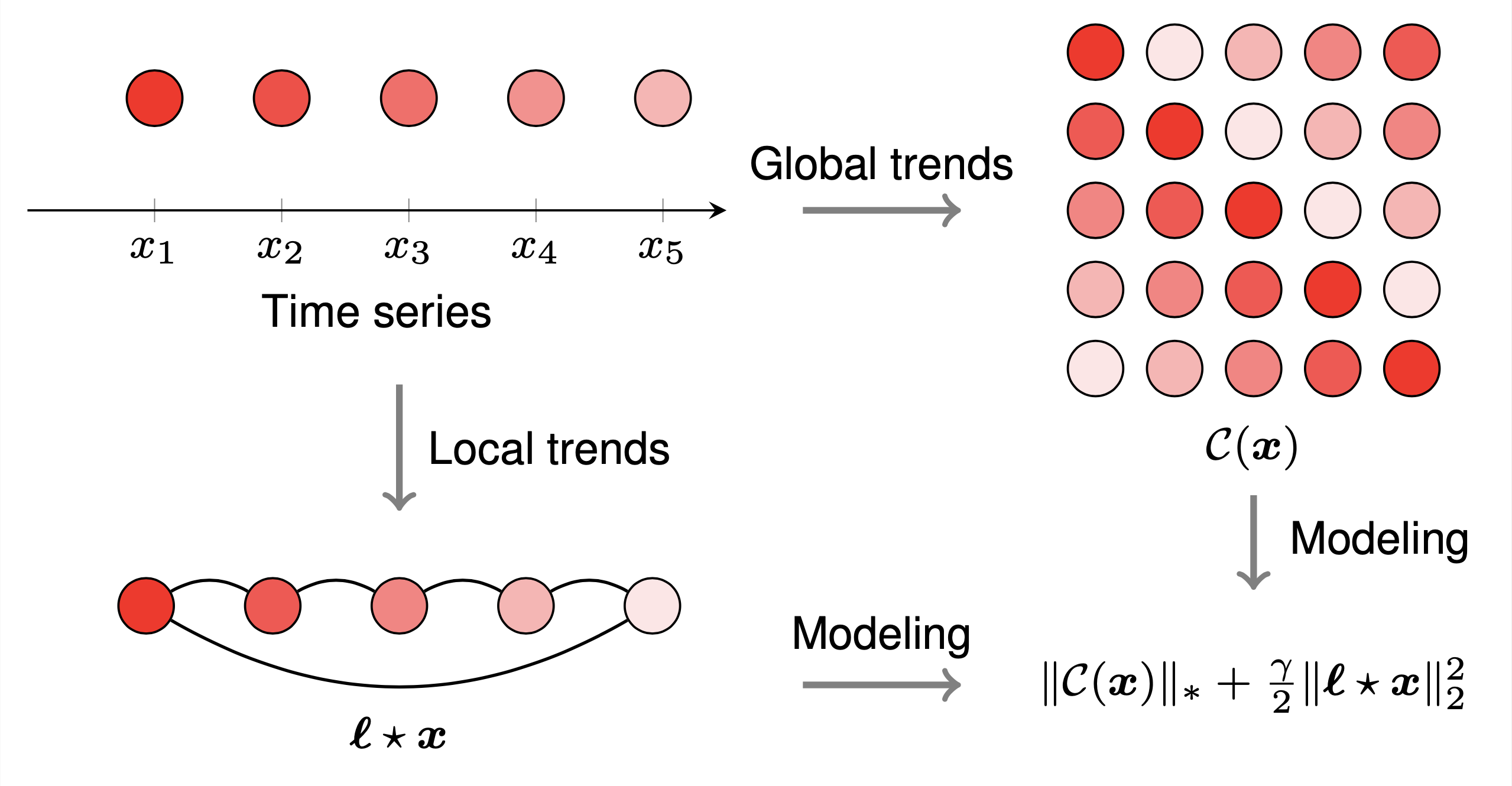
Cet exemple est tiré de l'article suivant :
Xinyu Chen, Zhanhong Cheng, Nicolas Saunier, Lijun Sun (2022). Représentation convolutive laplacienne pour l'imputation de séries chronologiques de trafic. Préimpression arXiv arXiv : 2212.01529.
qui donne une illustration graphique du modèle convolutionnel laplacien pour l'imputation de séries chronologiques. Pour dessiner l’exemple, nous pouvons suivre ces étapes :
preamble :documentclass comme standalone ,tikz .body :begin{tikzpicture} end{tikzpicture} pour commencer à dessiner,begin{axis} end{axis} et addplot pour dessiner les coordonnées,node et path pour dessiner des nœuds et des flèches.pgfplots Fonction Traçage 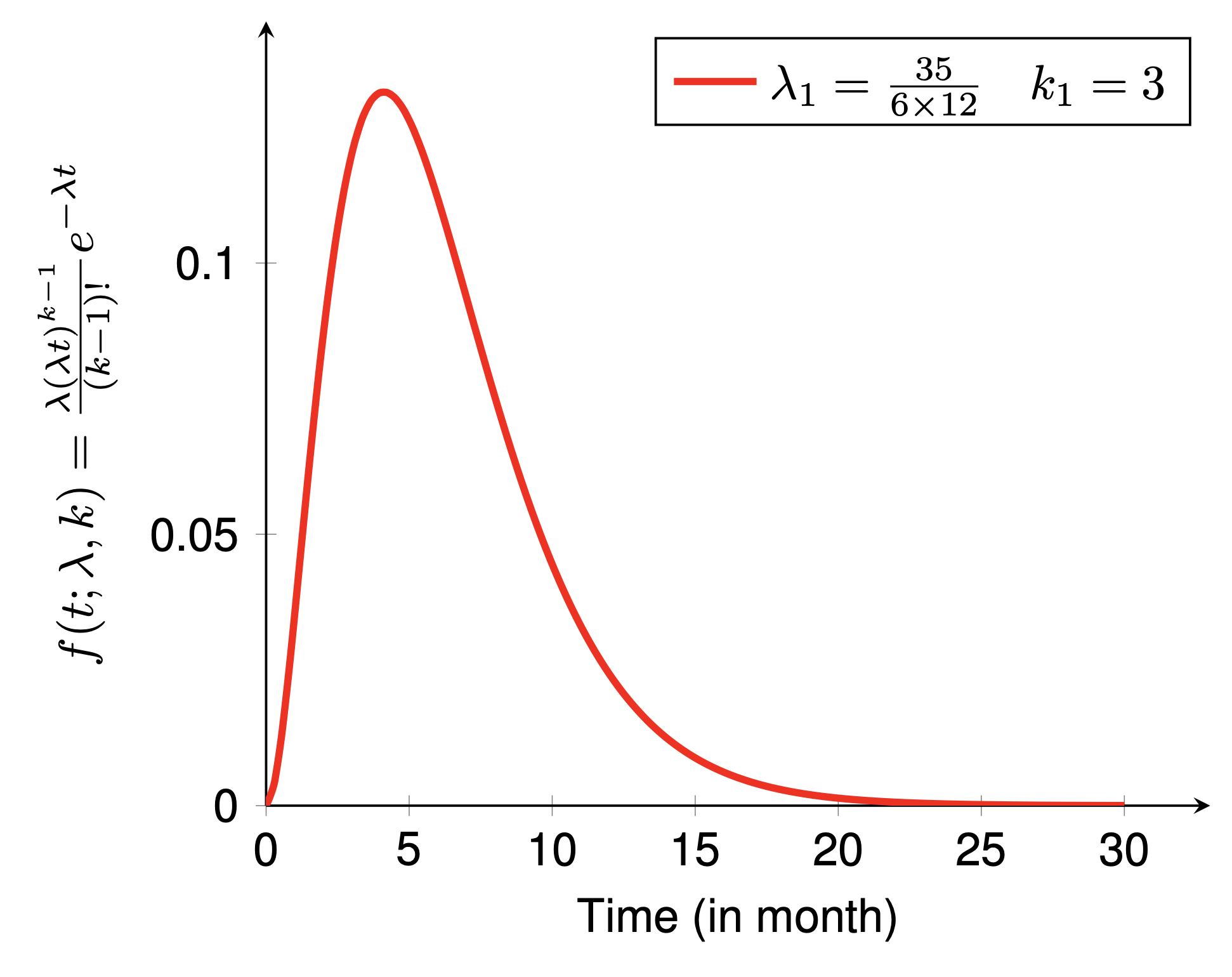
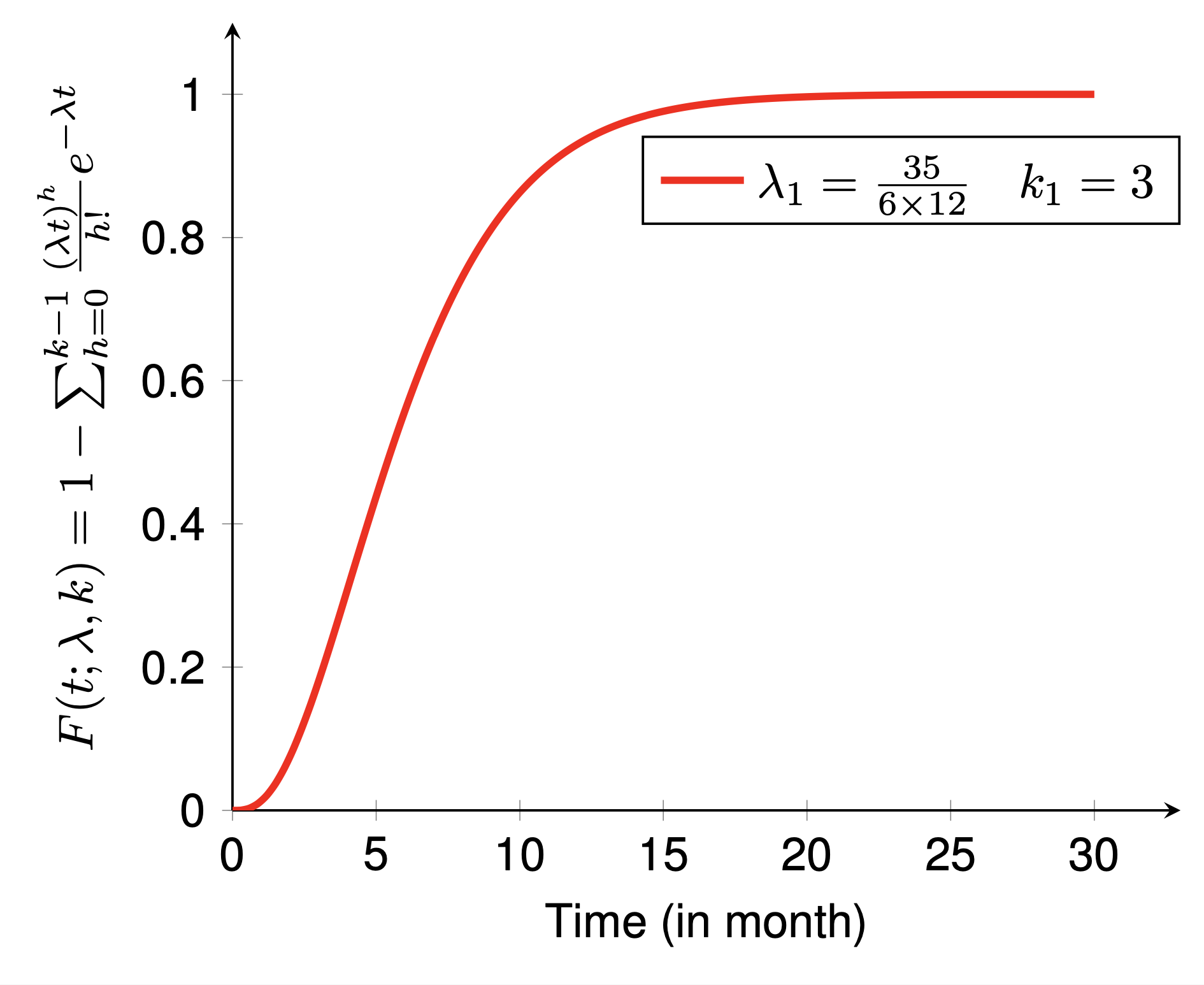
Ces deux exemples montrent respectivement la fonction de densité de probabilité (PDF) et la fonction de densité cumulative (CDF) de la distribution d'Erlang. Pour dessiner l’exemple, il y a quelques étapes à suivre :
preamble :documentclass comme standalone ,pgfplots ,pgfplotsset{} comme vous préférez.body :begin{tikzpicture} end{tikzpicture} pour commencer à dessiner,begin{axis} end{axis} pour dessiner la fonction,addplot pour définir la fonction de dessin. 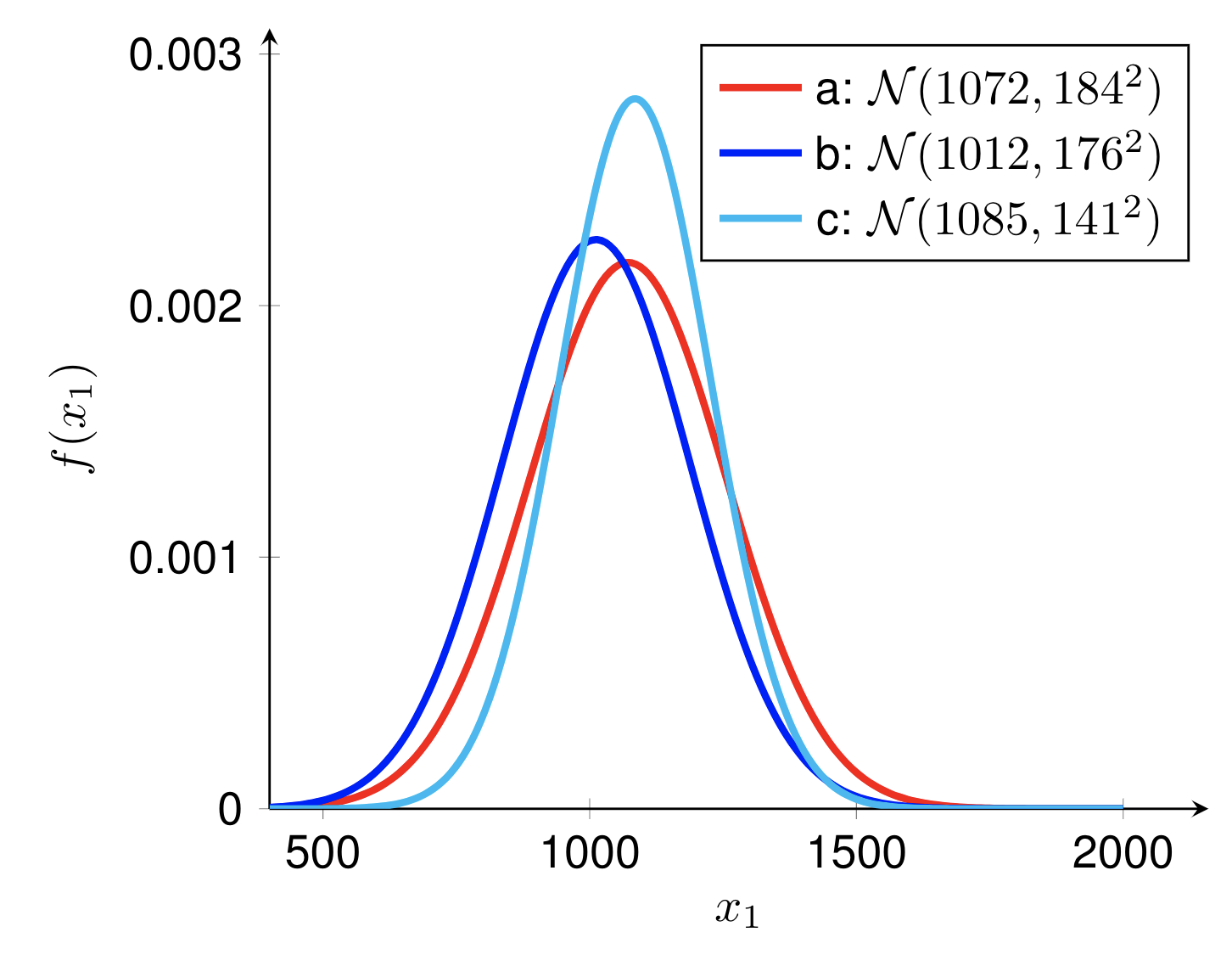
Cet exemple montre le PDF de distribution normale avec différentes moyennes et variances. Pour dessiner cet exemple, il y a quelques étapes à suivre :
preamble :documentclass comme standalone ,pgfplots ,pgfplotsset{} comme vous préférez.body :pgfmathdeclarefunction pour définir la fonction PDF de distribution normale (gaussienne),begin{tikzpicture} end{tikzpicture} pour commencer à dessiner,begin{axis} end{axis} pour dessiner la fonction,addplot pour définir la fonction de dessin.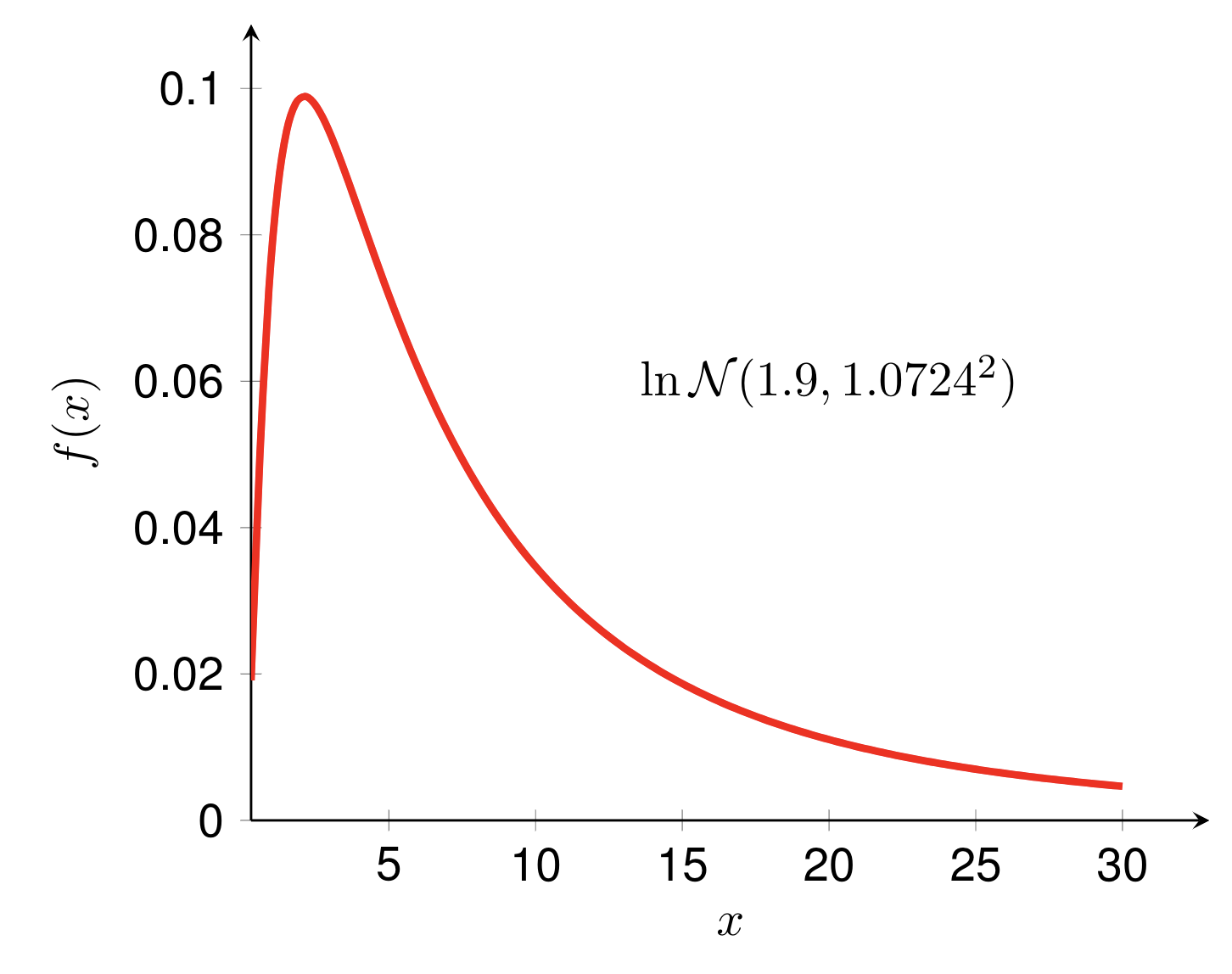
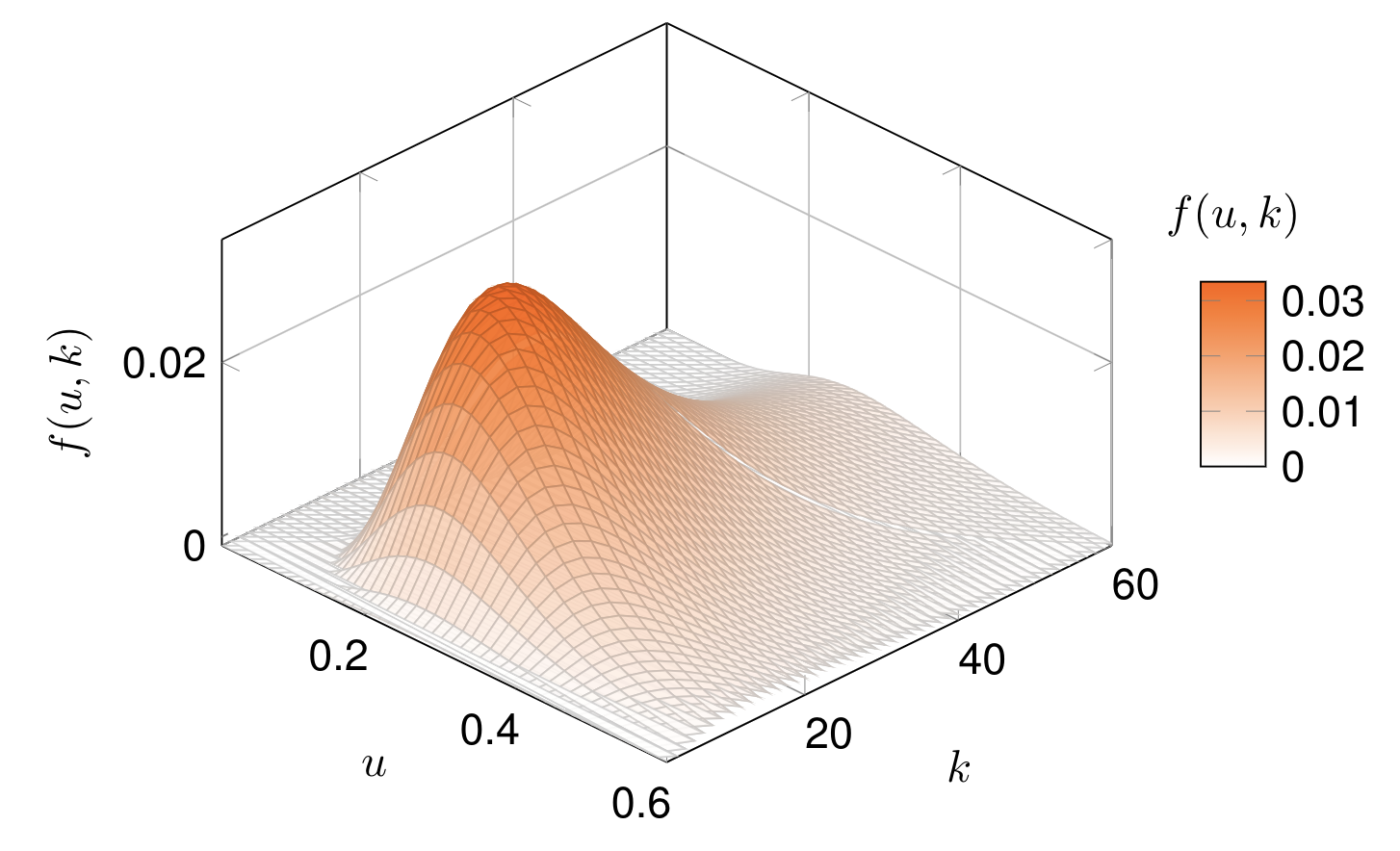
Ces deux exemples montrent respectivement le PDF et le PDF conjoint des distributions lognormales. Il existe du matériel recommandé pour suivre les exemples :
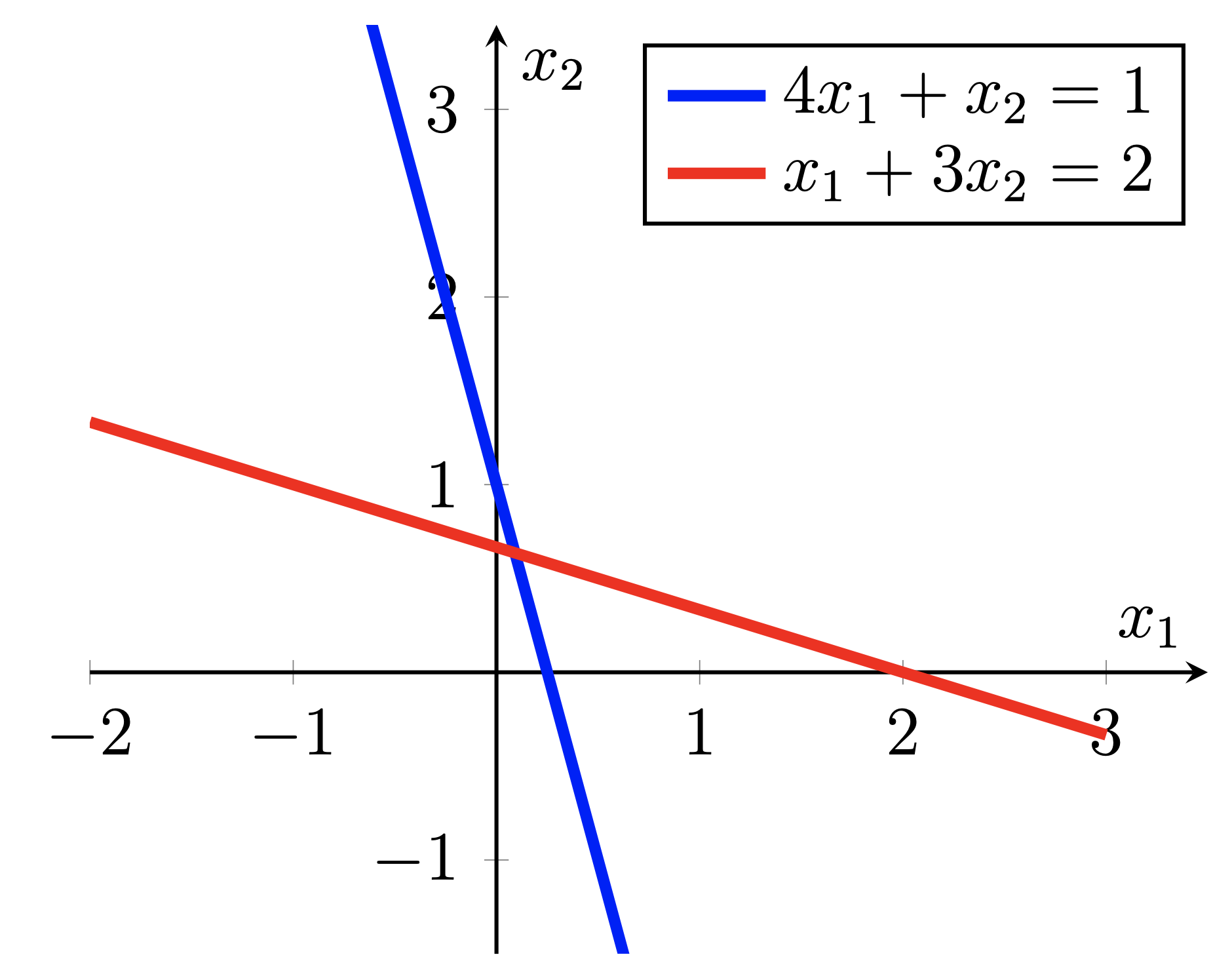
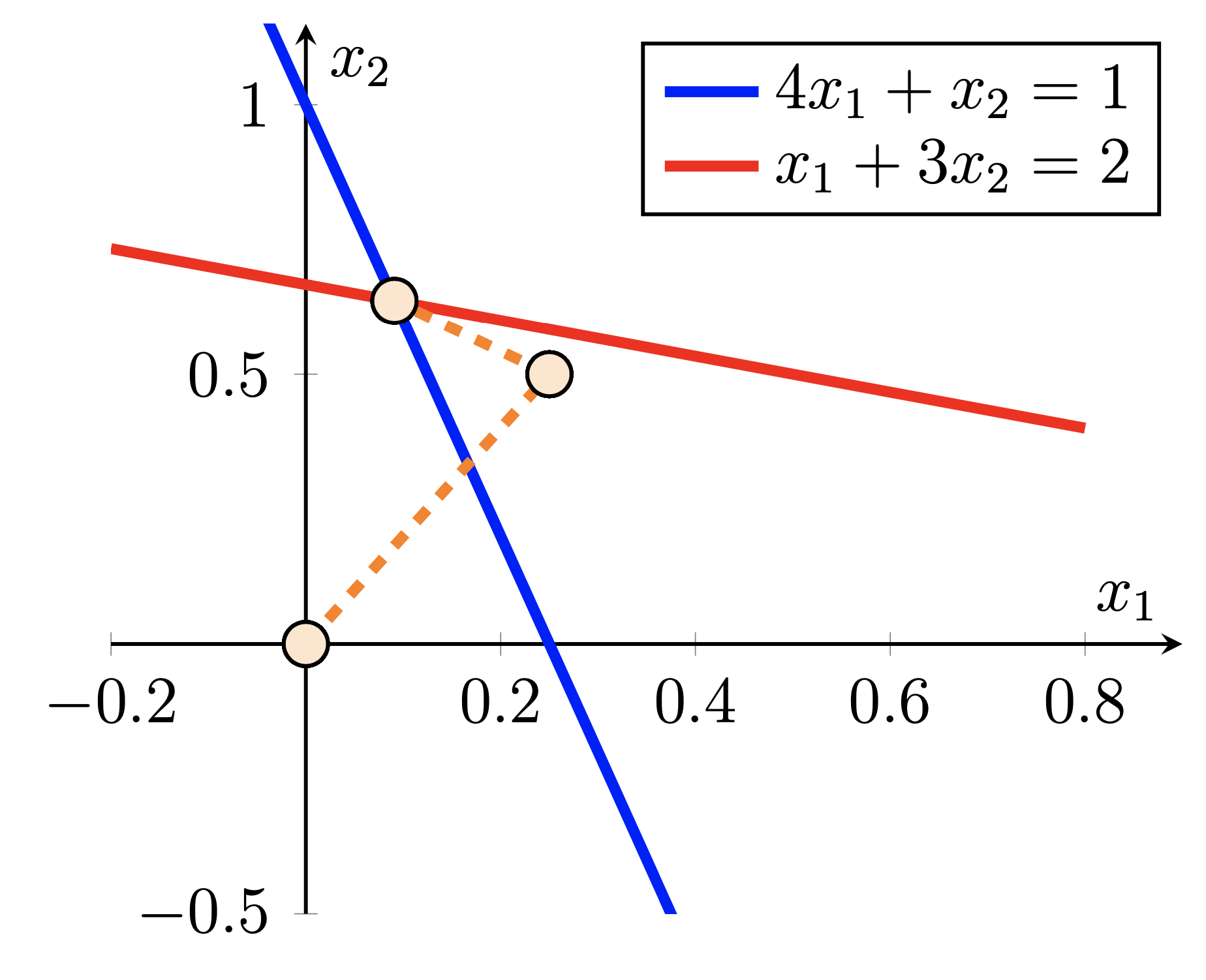
Ces deux exemples montrent le processus itératif de gradient conjugué pour résoudre un système d'équations linéaires.
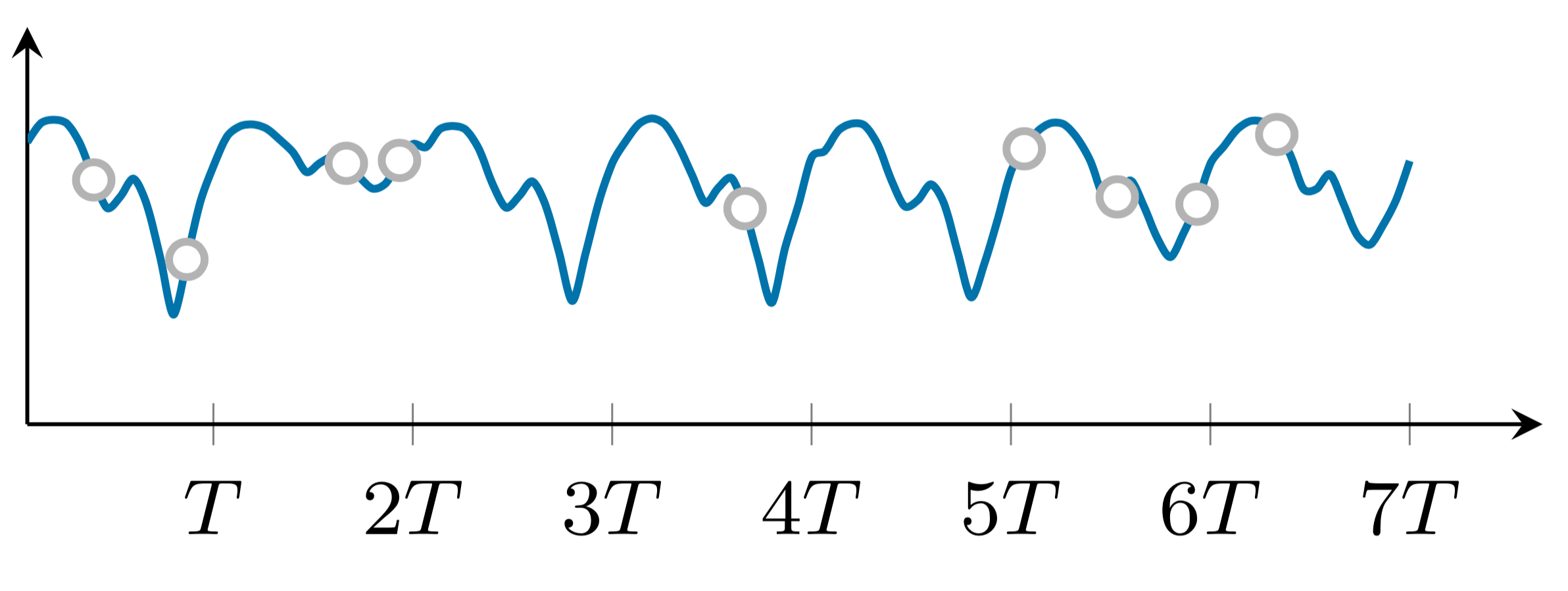
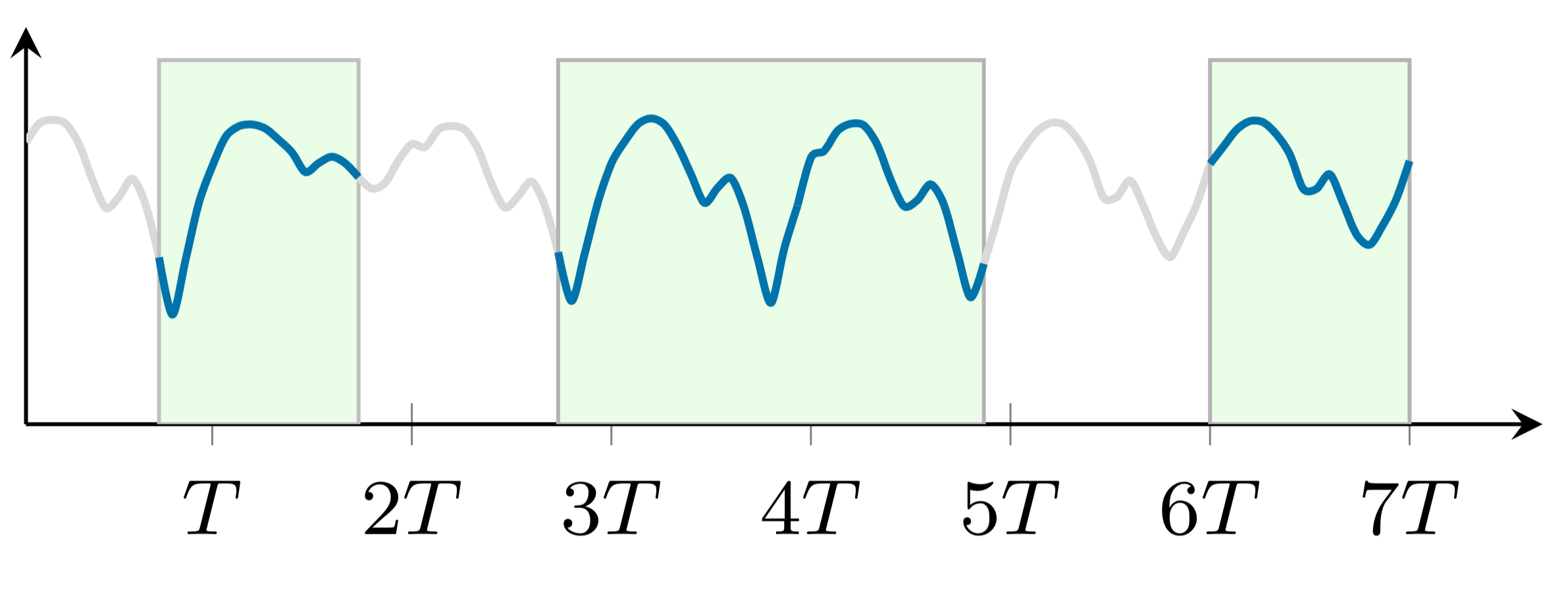
Ces deux exemples montrent les modèles manquants aléatoires et non aléatoires. Pour dessiner les deux exemples, nous pouvons suivre ces étapes :
preamble :documentclass comme standalone ,tikz et pgfplots ,begin{filecontents} end{filecontents} pour contenir les données.body :begin{tikzpicture} end{tikzpicture} pour commencer à dessiner,begin{axis} end{axis} pour dessiner la fonction,addplot pour dessiner les données. 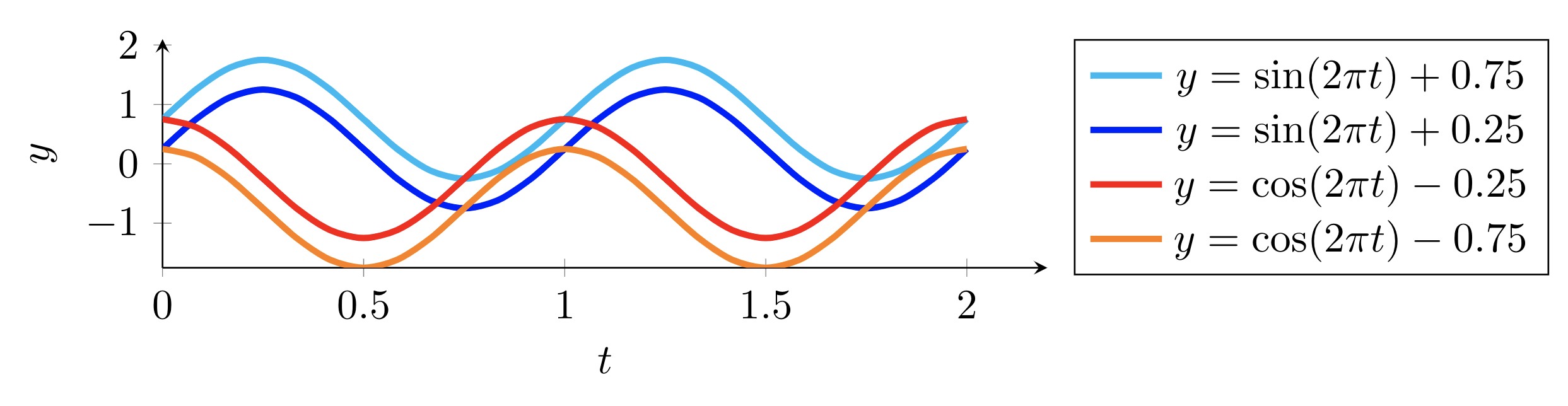
Cet exemple montre quatre séquences composées de fonctions sinus et cosinus. Lorsque l'on considère ces séquences comme des séries chronologiques, nous pouvons alors voir deux types de dynamique temporelle, c'est-à-dire que l'une provient de la fonction sinus, tandis qu'une autre provient de la fonction cosinus. Pour dessiner cet exemple, nous pouvons suivre ces étapes :
preamble :documentclass comme standalone ,pgfplots ,pgfplotsset{} comme vous préférez.body :pgfmathdeclarefunction pour définir la fonction PDF de distribution normale (gaussienne),begin{tikzpicture} end{tikzpicture} pour commencer à dessiner,begin{axis} end{axis} pour dessiner la fonction,addplot pour définir la fonction de dessin. Cet exemple illustre le mécanisme de prévision de séries chronologiques sur des données en streaming dans notre projet tracebase. Pour dessiner cet exemple, nous pouvons suivre ces étapes :
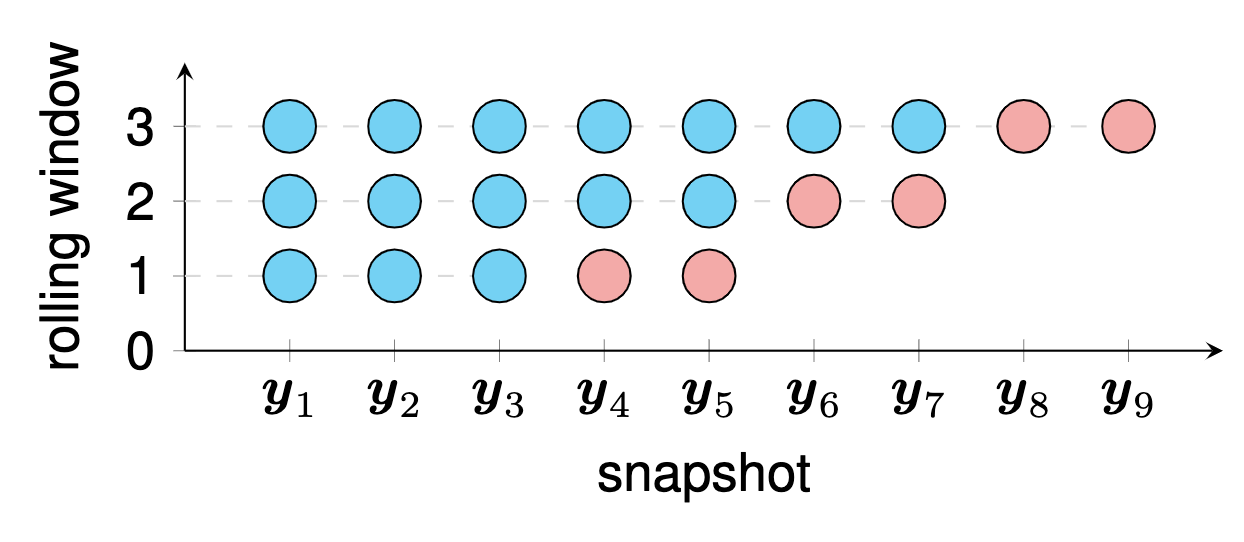
preamble :documentclass comme standalone ,tikz et pgfplots ,pgfplotsset{} comme vous préférez.body :begin{tikzpicture} end{tikzpicture} pour commencer à dessiner,begin{axis} end{axis} pour définir le graphique,addplot pour définir les marques à certaines coordonnées et spécifier la couleur de ces marques.tikz pour la structure matricielle 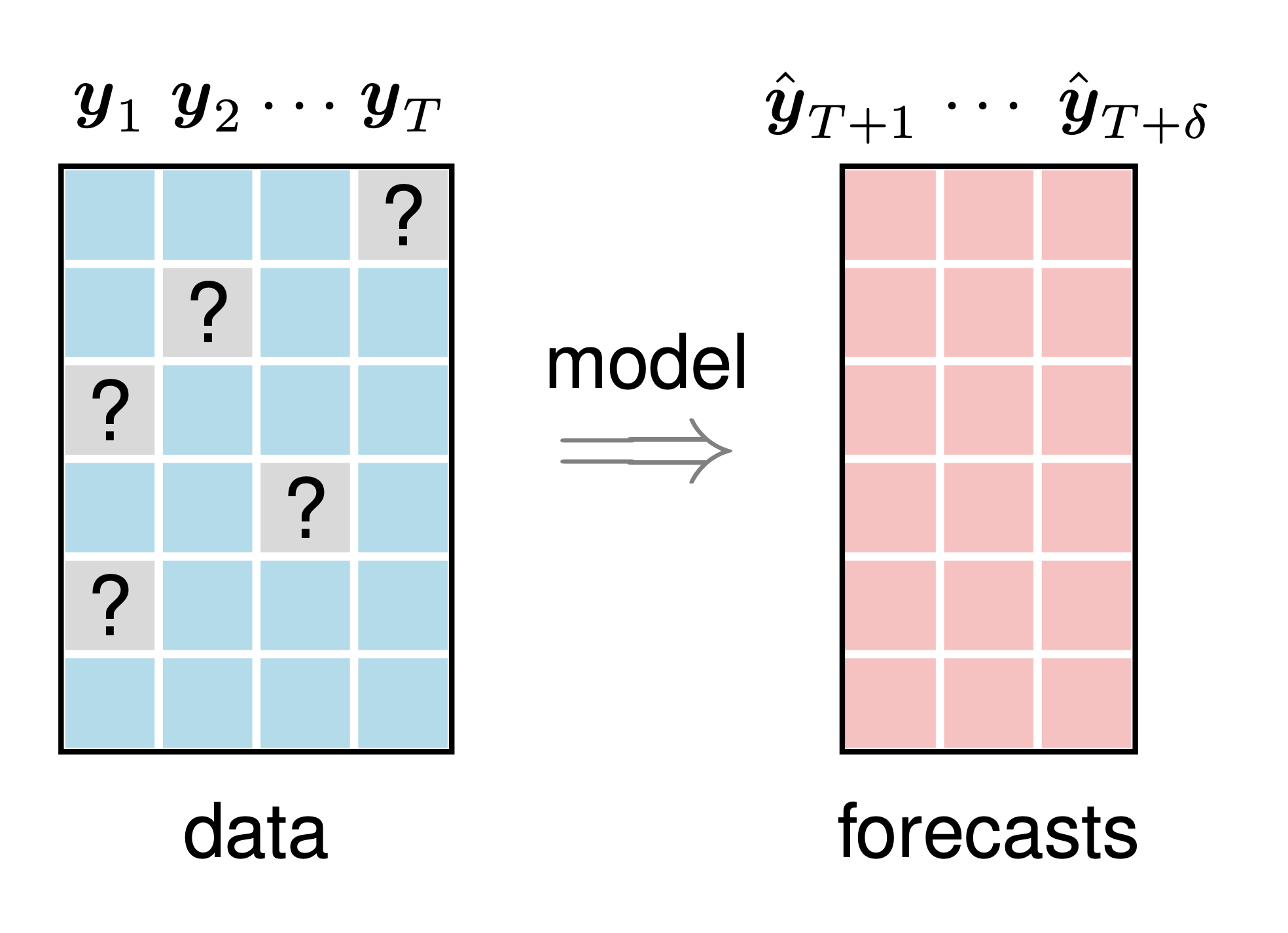
Cet exemple donne une illustration graphique du problème de prévision de séries chronologiques multivariées avec des valeurs manquantes. Pour dessiner cet exemple, nous pouvons suivre ces étapes :
preamble :documentclass comme standalone ,tikz .body :Depth , Width et Height à l'aide de newcommand ,begin{tikzpicture} end{tikzpicture} pour commencer à dessiner,draw , filldraw et node pour définir des rectangles et des nœuds. 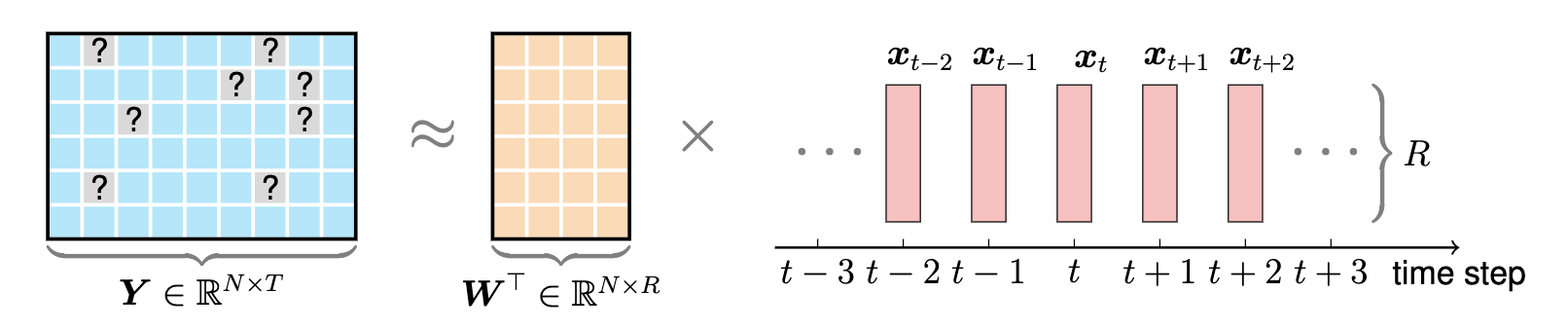
Cet exemple donne une illustration graphique de la factorisation matricielle temporelle. Pour dessiner cet exemple, nous pouvons suivre ces étapes :
preamble :documentclass comme standalone ,tikz .body :begin{tikzpicture} end{tikzpicture} pour commencer à dessiner,draw et filldraw pour définir les nœuds et les rectangles. 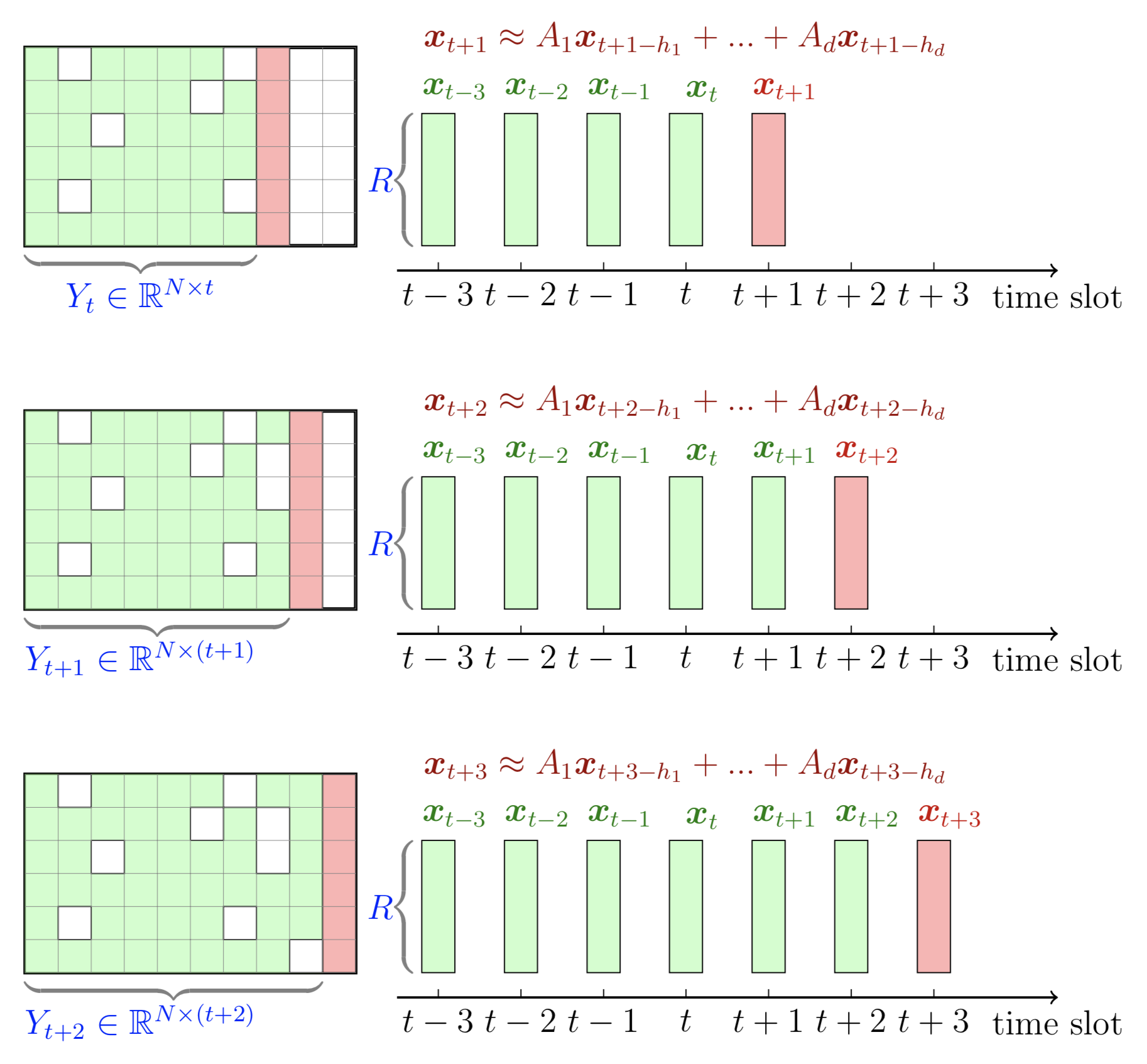
Cet exemple donne une illustration graphique de la prévision de séries temporelles glissantes avec factorisation matricielle temporelle. Pour dessiner cet exemple, nous pouvons suivre ces étapes :
preamble :documentclass comme standalone ,tikz .body :begin{tikzpicture} end{tikzpicture} pour commencer à dessiner,draw et filldraw pour définir les nœuds et les rectangles.tikz-3dplot pour la structure tensorielle Cet exemple donne une illustration graphique d'un tenseur du troisième ordre. Pour dessiner cet exemple, nous pouvons suivre ces étapes :
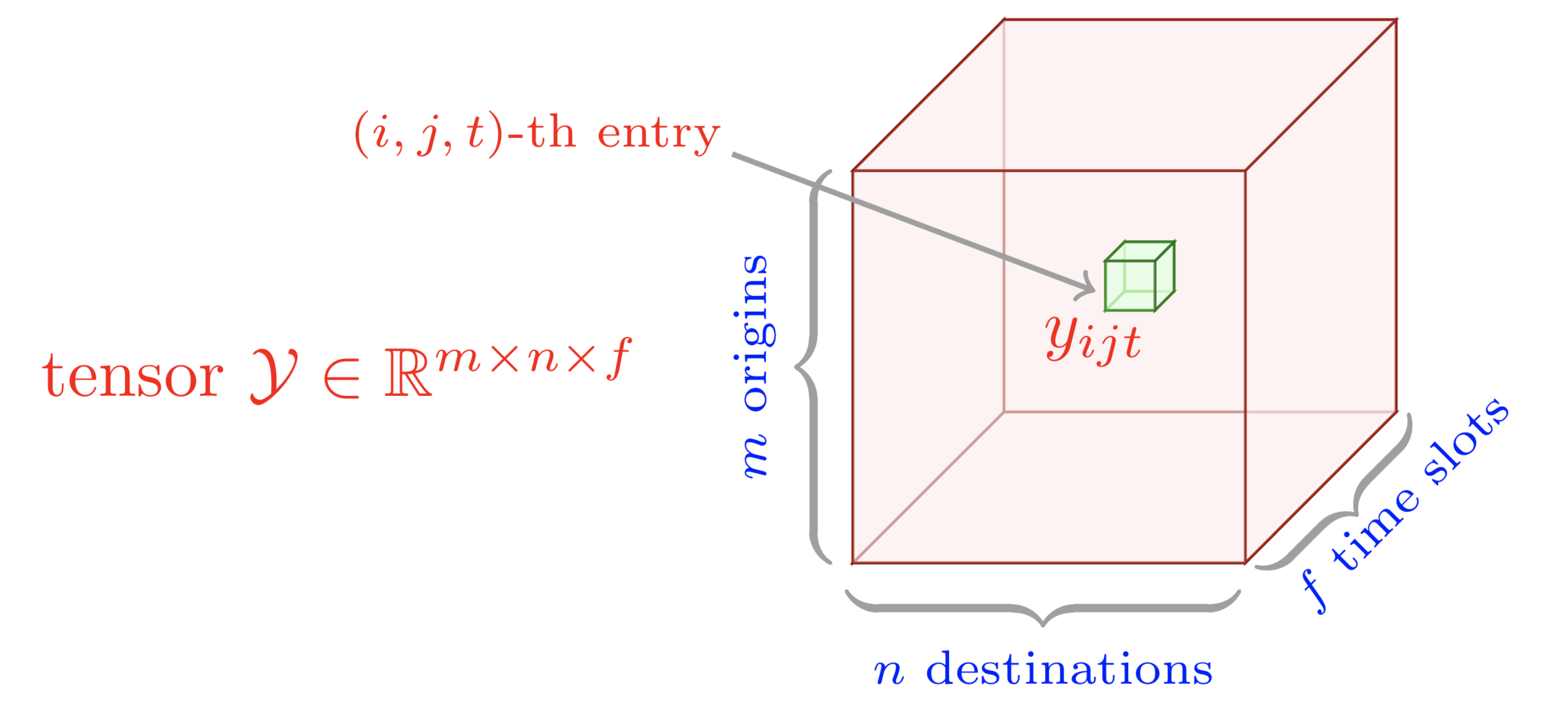
preamble :documentclass comme standalone ,tikz et tikz-3dplot .body :Depth , Width et Height à l'aide de newcommand ,begin{tikzpicture} end{tikzpicture} pour commencer à dessiner,draw pour définir les nœuds. Cet exemple donne une illustration graphique de la factorisation classique du tenseur CP sur un tenseur du troisième ordre. Pour dessiner cet exemple, nous pouvons suivre ces étapes :
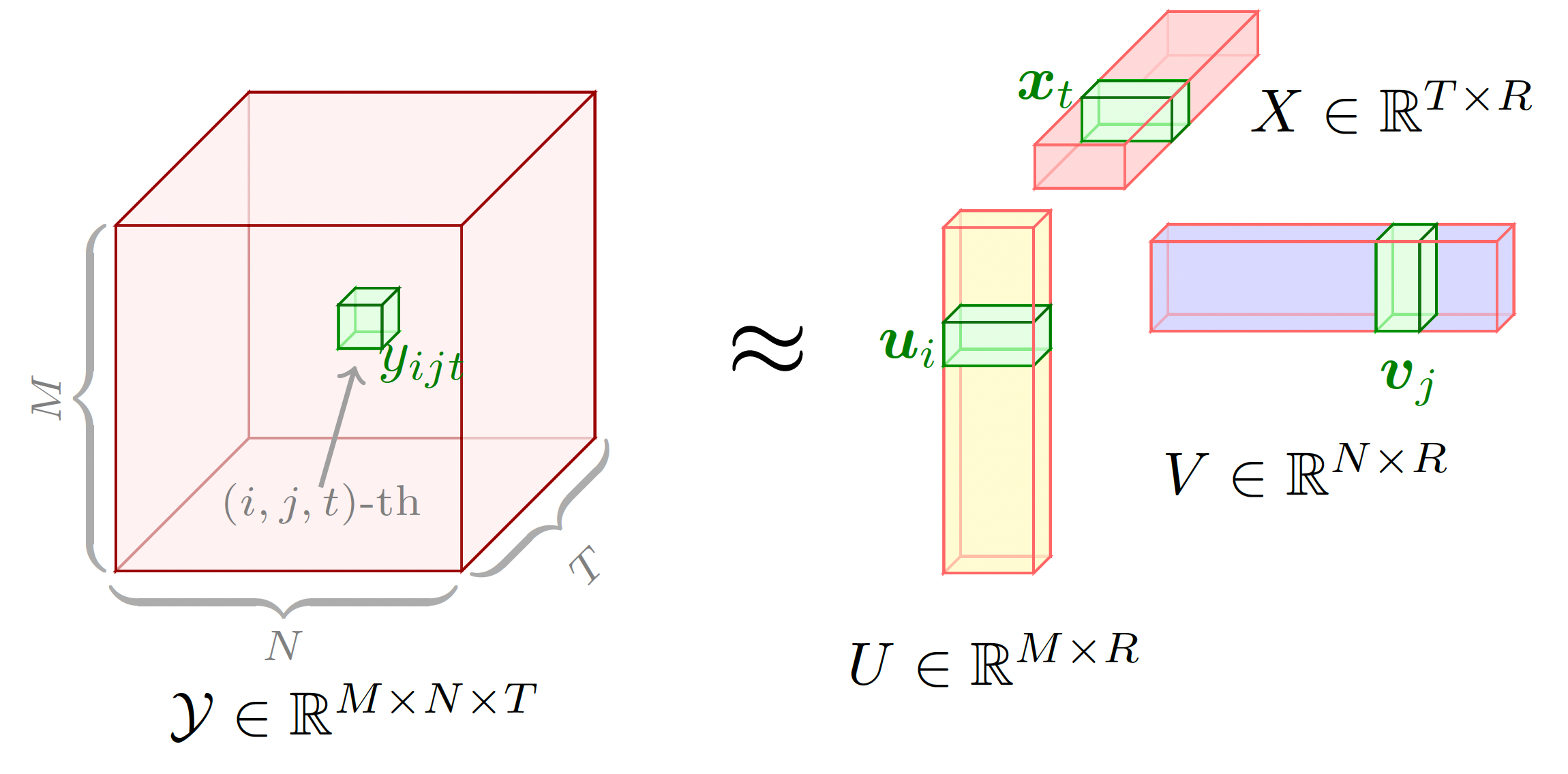
preamble :documentclass comme standalone ,tikz et tikz-3dplot .body :Depth , Width et Height à l'aide de newcommand ,begin{tikzpicture} end{tikzpicture} pour commencer à dessiner,draw pour définir les nœuds. 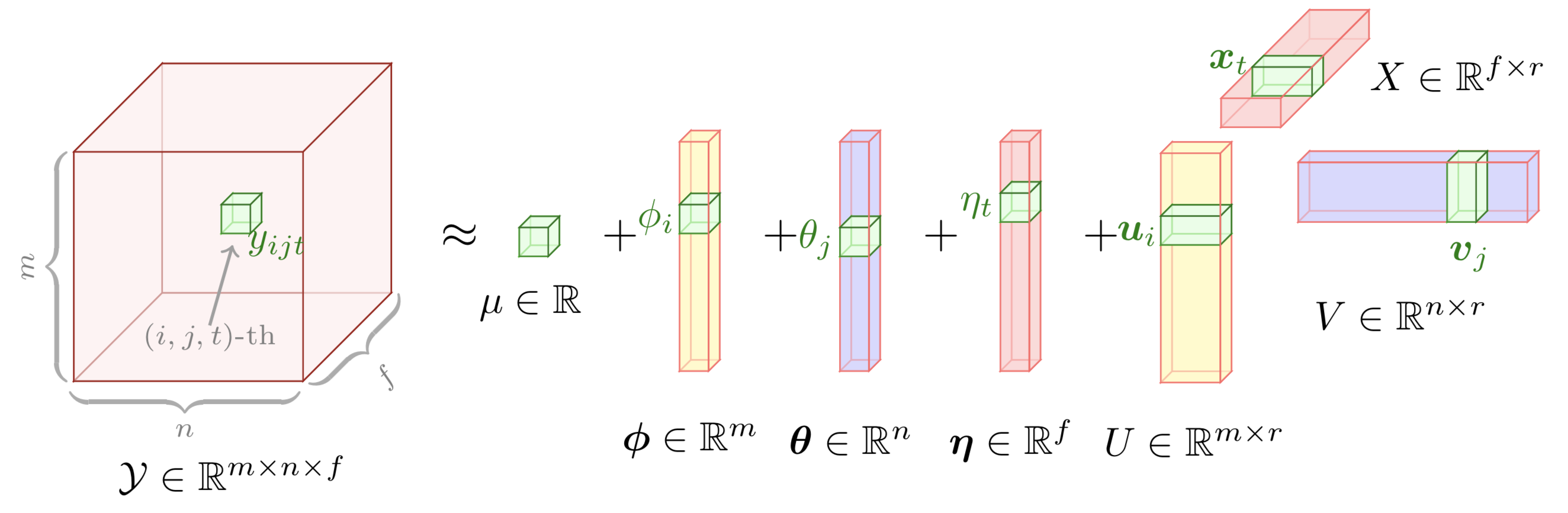
Cet exemple donne une illustration graphique du modèle de factorisation tensorielle augmentée. Pour dessiner cet exemple, nous pouvons suivre ces étapes :
preamble :documentclass comme standalone ,tikz et tikz-3dplot .body :Depth , Width et Height à l'aide de newcommand ,begin{tikzpicture} end{tikzpicture} pour commencer à dessiner,draw pour définir les nœuds. 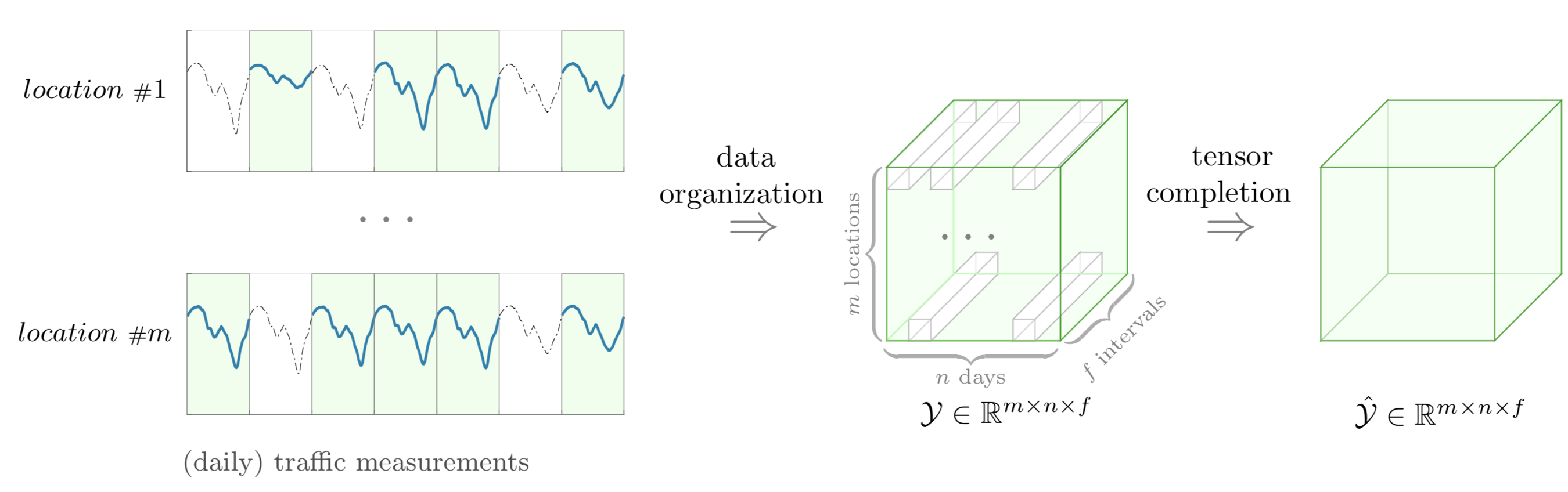
Cet exemple donne une illustration graphique de la tâche de complétion du tenseur et de son cadre comprenant l'organisation des données et la complétion du tenseur, dans laquelle les mesures de trafic sont partiellement observées. Pour dessiner cet exemple, nous pouvons suivre ces étapes :
preamble :documentclass comme standalone ,tikz et tikz-3dplot .body :Depth , Width et Height à l'aide de newcommand ,begin{tikzpicture} end{tikzpicture} pour commencer à dessiner,draw pour définir les nœuds. 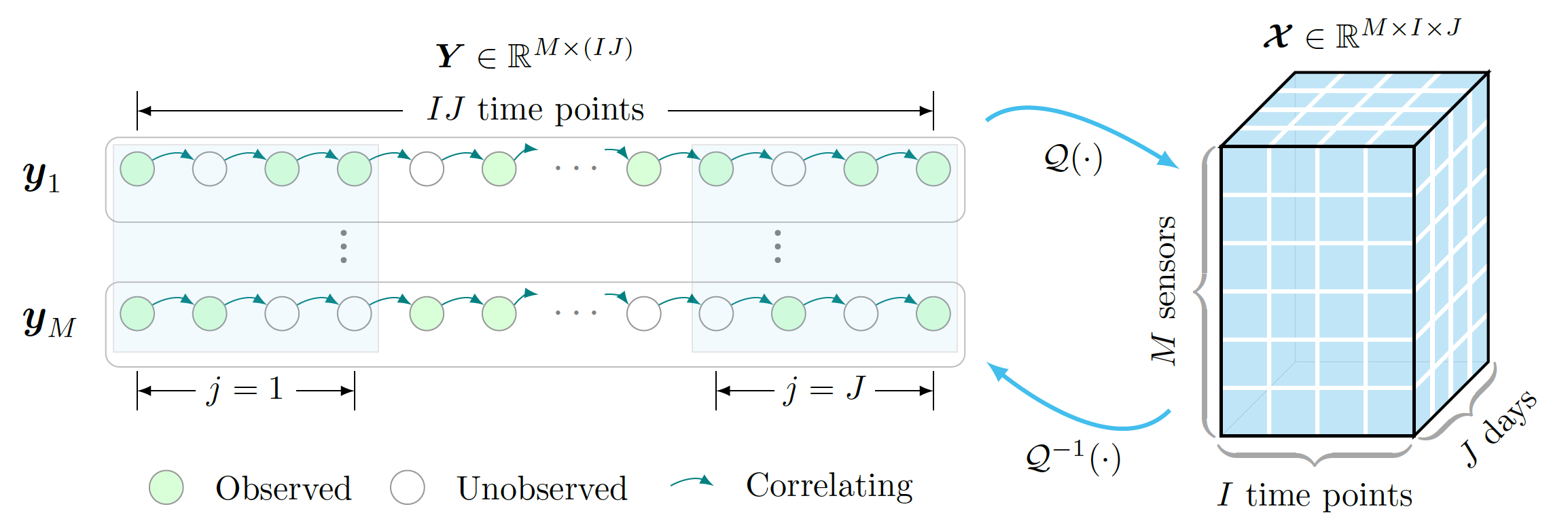
Cet exemple donne une illustration graphique du modèle d'achèvement de tenseur autorégressif de bas rang. Pour dessiner cet exemple, nous pouvons suivre ces étapes :
preamble :documentclass comme standalone ,tikz et tikz-3dplot .body :Depth , Width et Height à l'aide de newcommand ,begin{tikzpicture} end{tikzpicture} pour commencer à dessiner,node , path , plate pour définir des nœuds, des flèches et des plaques,draw pour définir les nœuds. Cet exemple donne une illustration graphique du processus de seuillage de valeurs singulières des données tensorielles avec transformation unitaire. Pour dessiner cet exemple, nous pouvons suivre ces étapes :
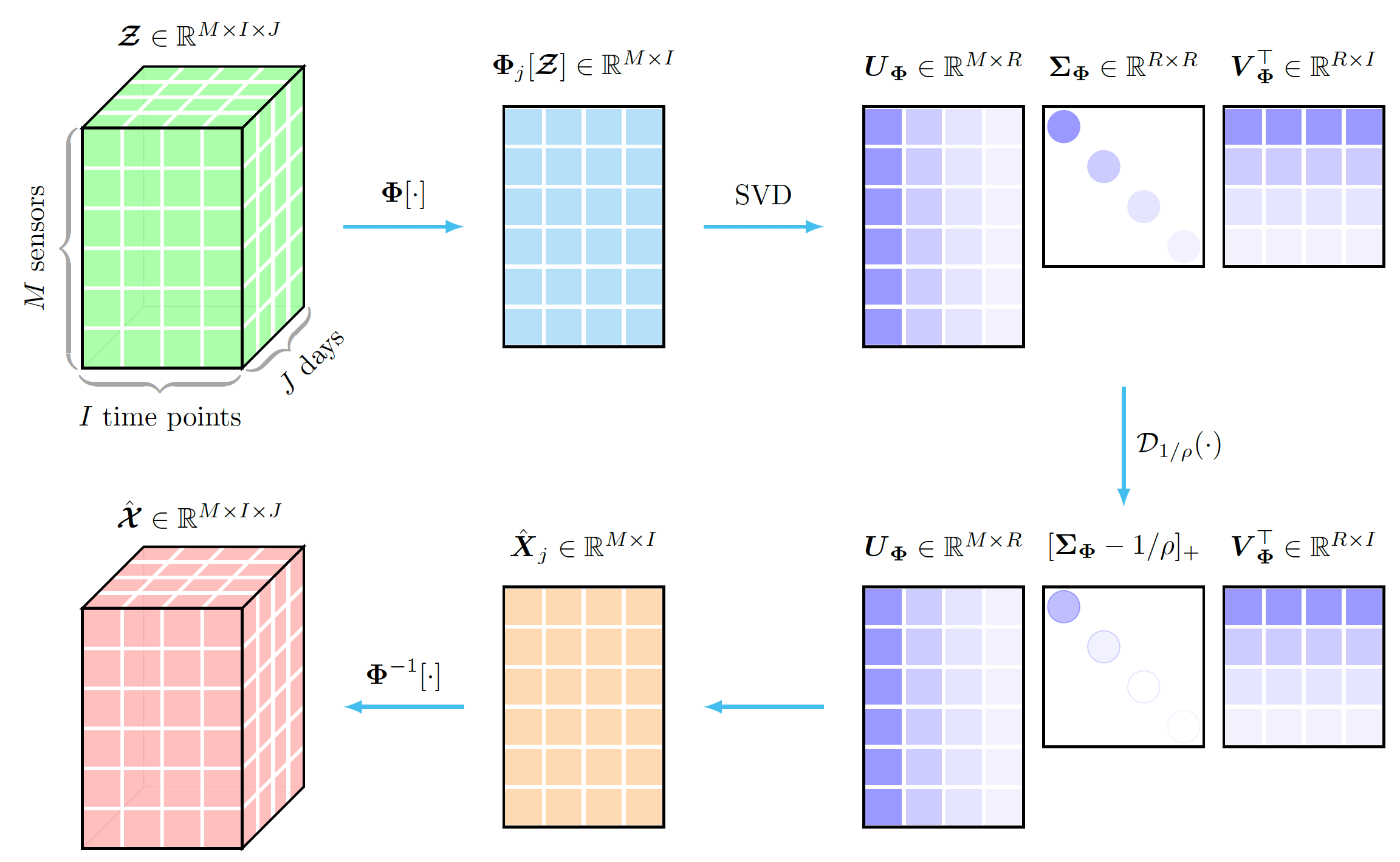
preamble :documentclass comme standalone ,tikz et tikz-3dplot .body :Depth , Width et Height à l'aide de newcommand ,begin{tikzpicture} end{tikzpicture} pour commencer à dessiner,node pour définir les nœuds,draw pour définir les nœuds,filldraw pour définir les couleurs des rectangles. 
Cet exemple donne une illustration graphique du modèle de complétion de tenseur de bas rang. Pour dessiner cet exemple, nous pouvons suivre ces étapes :
preamble :documentclass comme standalone ,tikz et tikz-3dplot ,algorithm2e ,usetikzlibrary{positioning, matrix, fit, calc} .body :begin{algorithm} end{algorithm} pour définir l'algorithme,matrix pour positionner les composants,begin{scope} end{scope} pour contenir les couches. 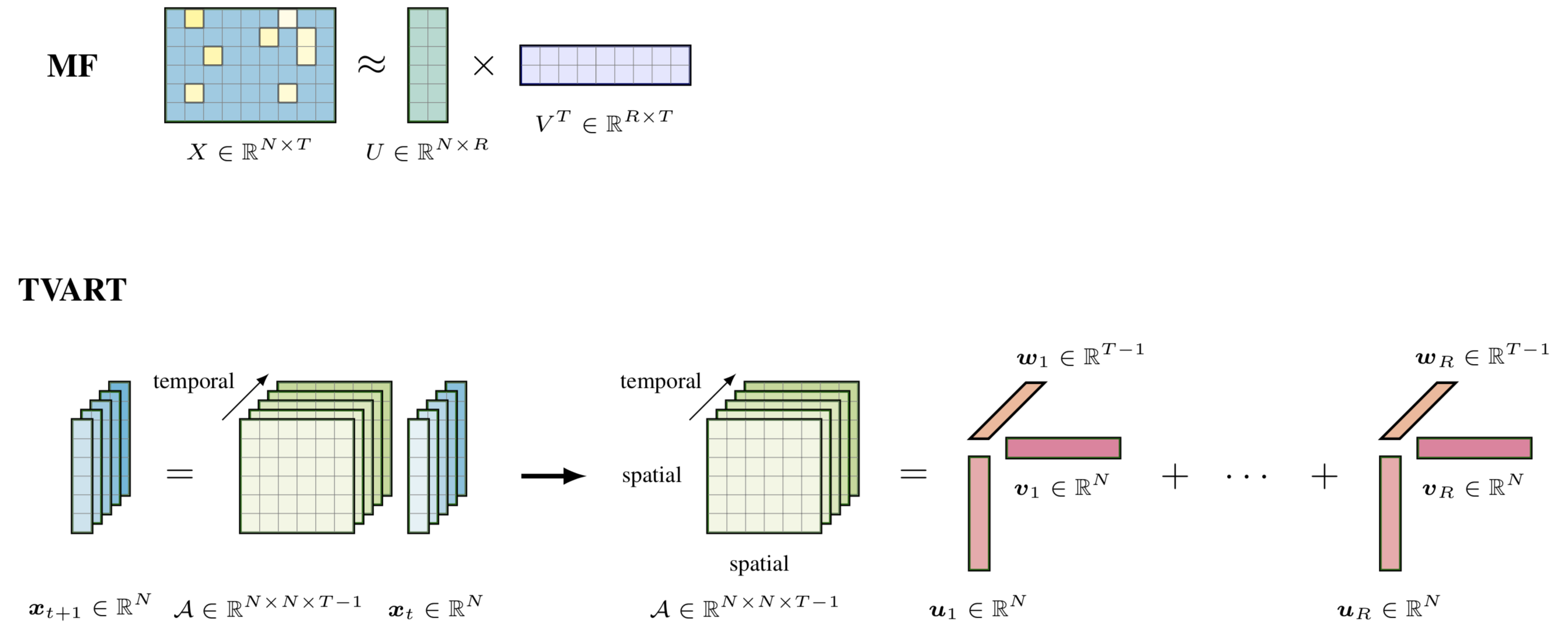
Cet exemple donne une illustration graphique du modèle de régression tenseur de bas rang. Pour dessiner cet exemple, nous pouvons suivre ces étapes :
preamble :documentclass comme standalone ,tikz et tikz-3dplot .body :Depth , Width et Height à l'aide de newcommand ,begin{tikzpicture} end{tikzpicture} pour commencer à dessiner,draw pour définir les nœuds.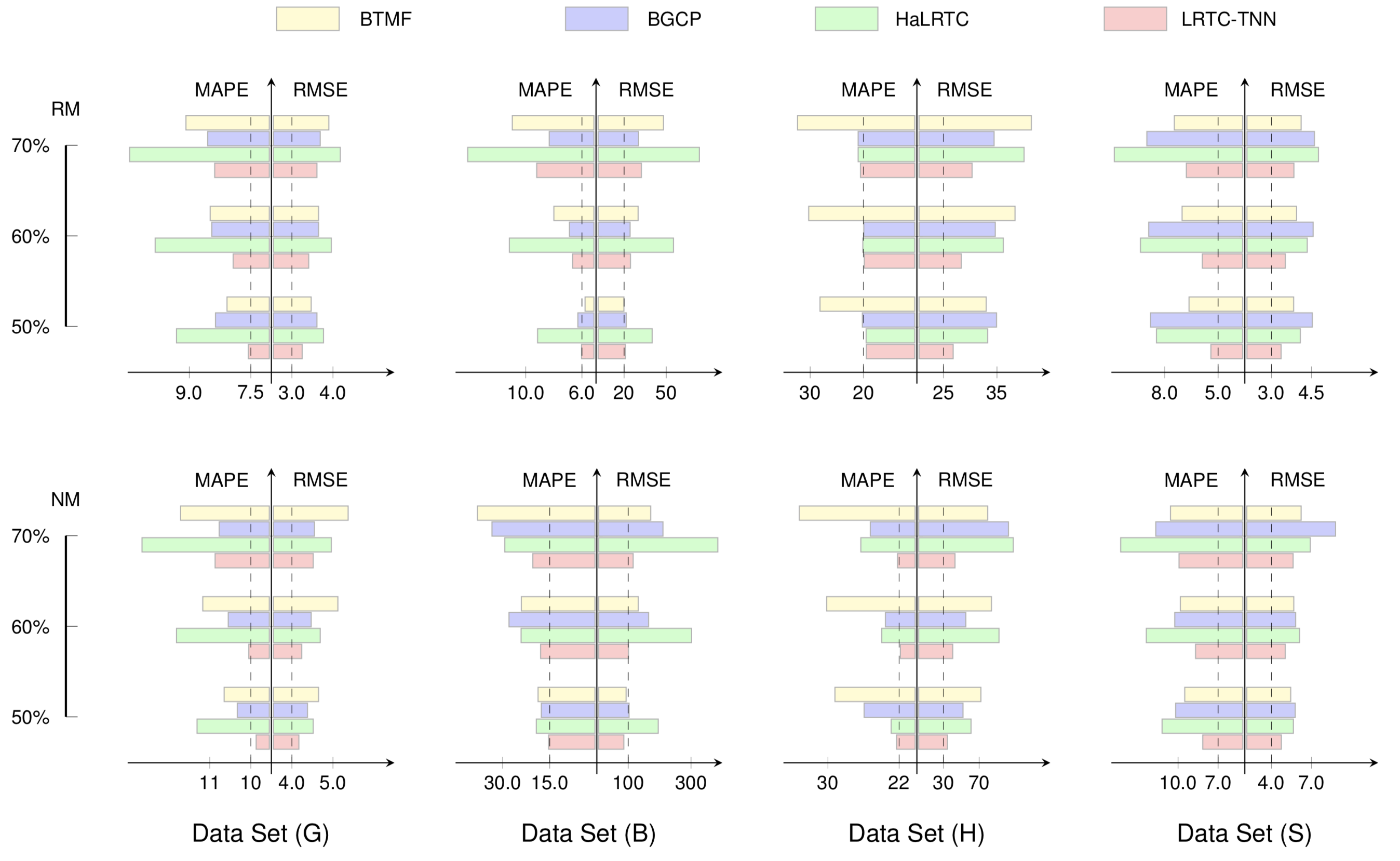
Cet exemple montre la précision de l'imputation de certains modèles matriciels et tensoriels. Pour dessiner cet exemple, nous pouvons suivre ces étapes :
preamble :documentclass comme standalone ,tikz .body :begin{tikzpicture} end{tikzpicture} pour commencer à dessiner,draw pour définir les nœuds,pgfuseimage pour importer des images. La plupart de ces exemples proviennent de nos articles :
Xinyu Chen, Zhanhong Cheng, HanQin Cai, Nicolas Saunier, Lijun Sun (2024). "Représentation convolutionnelle laplacienne pour l'imputation de séries chronologiques de trafic" . Transactions IEEE sur l'ingénierie des connaissances et des données, 36 (11) : 6490-6502. [Préimpression] [DOI] [Slides] [Données et code Python]
Xinyu Chen, Lijun Sun (2022). Factorisation temporelle bayésienne pour la prédiction de séries chronologiques multidimensionnelles . Transactions IEEE sur l'analyse de modèles et l'intelligence artificielle, 44 (9) : 4659-4673. [Préimpression] [DOI] [Slides] [Données et code Python]
Xinyu Chen, Mengying Lei, Nicolas Saunier, Lijun Sun (2022). "Achèvement du tenseur autorégressif de bas rang pour l'imputation des données de trafic spatio-temporelles" . Transactions IEEE sur les systèmes de transport intelligents, 23 (8) : 12301-12310. [Preprint] [DOI] [Data & Python code] (Également accepté en partie à l'atelier MiLeTS du KDD 2021, voir le document de l'atelier)
Xinyu Chen, Yixian Chen, Nicolas Saunier, Lijun Sun (2021). Apprentissage tenseur de bas rang évolutif pour l'imputation de données de trafic spatio-temporelles . Recherche sur les transports, partie C : Technologies émergentes, 129 : 103226. [Préimpression] [DOI] [Données] [Code Python]
Xinyu Chen, Lijun Sun (2020). "Achèvement du tenseur autorégressif de bas rang pour la prévision de séries chronologiques multivariées" . Préimpression arXiv arXiv : 2006.10436. [Préimpression] [Données et code Python]
Xinyu Chen, Jinming Yang, Lijun Sun (2020). "Un modèle d'achèvement de tenseur de bas rang non convexe pour l'imputation de données de trafic spatio-temporelles" . Recherche sur les transports, partie C : Technologies émergentes, 117 : 102673. [Préimpression] [DOI] [Données et code Python]
Xinyu Chen, Zhaocheng He, Yixian Chen, Yuhuan Lu, Jiawei Wang (2019). Imputation des données de trafic manquantes et découverte de modèles avec un modèle de factorisation tenseur augmenté bayésien . Recherche sur les transports, partie C : Technologies émergentes, 104 : 66-77. [DOI] [Diapositives] [Données] [Code Matlab] [Code Python]
Xinyu Chen, Zhaocheng He, Lijun Sun (2019). "Une approche de décomposition tensorielle bayésienne pour l'imputation de données de trafic spatio-temporelles" . Recherche sur les transports, partie C : Technologies émergentes, 98 : 73-84. [Préimpression] [DOI] [Données] [Code Matlab] [Code Python]